基于EEMD-PSR-CS-SVR组合方法的PM2.5浓度预测模型研究

刘 微 陈福集

(福州大学经济与管理学院， 福建福州 350108)

环境污染问题已成为全球面临的重大挑战，特别是大气污染方面，雾霾问题严重影响社会发展和人类身体健康。即使在浓度相对低的情况下，具有危害性的大气颗粒物也会对人类健康和生态系统造成严重的破坏，尤其是由细小颗粒组成的PM2.5(指环境空气中空气动力学当量直径小于2.5μm的颗粒物，也称细颗粒物)可以更深入渗透到人类呼吸系统中(1)Dockery D.W., Pope C.A.,“Acute Respiratory Effects of Particulate Air Pollution”,Annual Review of Public Health, vol.15,no.1(1994),pp.107-132.，增加人们罹患心血管和肺部疾病的风险(2)Turner M. C., Krewski D., III Pope C.A., et al.,“Long-term ambient fine particulate matter air pollution and lung cancer in a large cohort of never-smokers”，American Journal of Respiratory & Critical Care Medicine, vol.184,no.12(2011),pp.1374-1381.。因此，空气中PM2.5的浓度一直是全球关注的焦点，掌握其变化规律并预测未来一段时间内的PM2.5浓度，具有重要的现实意义。

PM2.5来源较为复杂，如燃煤、扬尘、汽车尾气、工业污染等(3)伯鑫、徐峻、杜晓惠，等：《京津冀地区钢铁企业大气污染影响评估》，《中国环境科学》2017年第5期。，特别是在我国的较大城市，机动车排放是PM2.5的首要来源。(4)中华人民共和国生态环境部：《中国机动车环境管理年报》，2018年。而影响PM2.5浓度的因素众多，主要包括气象因素(如大气压强、相对湿度、温度、风速、风向、累计降水量等)和污染物因素(如PM10、NOx、CO、SO2、O3等)(5)Liang X., Zou T., Guo B., et al.,“Assessing Beijing's PM2.5 pollution: severity, weather impact, APEC and winter heating”，Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences, vol.471(2015),p.257.，它们之间的关系较为复杂，很难进行数学建模，使得PM2.5浓度变化具有非线性、非平稳性等特点，因此对其进行预测具有一定的难度。随着统计方法、数据挖掘等智能信息处理技术的发展，国内外学者对PM2.5浓度的预测研究取得了很大进展。近几年来，神经网络在非线性预测方面得到广泛应用，Franceschi等使用神经网络技术结合聚类和主成分分析算法，对PM2.5和PM10的浓度和分类进行了预测。(6)Franceschi F., Cobo M., Figuereredo M.,“Discovering relationships and forecasting PM10 and PM2.5 concentrations in Bogotá, Colombia, using Artificial Neural Networks, Principal Component Analysis, and k-means clustering”，Atmospheric Pollution Research, no.9(2018),pp.912-922.支持向量机技术使用训练数据中的一小部分样本建立模型，采用松弛变量和核函数来处理非线性问题，能够简化计算复杂度，提高运算速度，进一步结合现代优化算法选取合适的参数，能更有效地提高预测效果。(7)Cortes C., Vapnik V.,“Support-vector networks”，Machine Learning, vol.20,no.3(1995),pp.273-297.Sun等提出了一种基于主成分分析和布谷鸟搜索优化的最小二乘支持向量机(LSSVM)组合模型，可用于对PM2.5日平均浓度进行预测。(8)Sun W., Sun J.,“Daily PM2.5 concentration prediction based on principal component analysis and LSSVM optimized by cuckoo search algorithm”，Journal of Environmental Management, vol.188(2017),pp.144-152.在前期工作中，我们也运用气象模式分析辅助粒子群优化的支持向量机算法(PSO-SVM)对PM2.5浓度进行了等级分类，获得较高的分类精度和效率。(9)Liu W.,Guo G.,Chen F.,et al.,“Meteorological pattern analysis assisted daily PM2.5 grades prediction using SVM optimized by PSO algorithm”，Atmospheric Pollution Research, vol.10(2019),pp.1482-1491.

针对时间序列问题，经验模态分解(empirical mode decomposition, EMD)算法速度快，能较快地捕捉到不同尺度下的序列特征信息，但是其也存在模态混叠的问题(10)Huang N.E.,Shen Z.,Long S.R.,et al.,“The empirical mode decomposition method and the Hilbert spectrum for non-stationary time series analysis”，Proceedings of Royal Society of London, vol.454(1998),pp.903-995.，而集合经验模态分解(ensemble empirical mode decomposition, EEMD)方法利用噪声的频率均匀分布的统计特性弥补了这一不足。(11)Wu Z.H.,Huang N.E.,“Ensemble empirical mode decomposition: a noise-assisted data analysis method”，Advances in Adaptive Data Analysis, vol.1,no.1(2009),pp.1-41.近年来，进一步将这类模态分解方法与支持向量机预测模型组合起来用于PM2.5浓度预测，可以提高预测精度。秦喜文等采用EEMD和支持向量回归的混合模型(EEMD-SVR)对北京市PM2.5浓度进行了预测，其结果比单纯利用SVR方法的精度有所提高。(12)秦喜文、刘媛媛、王新民，等：《基于整体经验模态分解和支持向量回归的北京市PM2.5预测》，《吉林大学学报》(地球科学版)2016年第2期。Niu等则采用互补集合经验模态分解(CEEMD)与灰狼算法优化参数的支持向量回归模型用于每日PM2.5浓度预测，得到了较为满意的结果。(13)Niu M.,Wang Y.,Sun S.,et al.,“A novel hybrid decomposition-and-ensemble model based on CEEMD and GWO for short-term PM2.5 concentration forecasting”，Atmospheric Environment, vol.134(2016),pp.168-180.相空间重构(phase space reconstruction, PSR)是分析混沌时间序列的前提和基础，根据Takens提出的嵌入理论，可以将一维时间序列重构成一个多维矩阵(14)Takens F.,Detecting strange attractors in turbulence, Lecture Notes in Mathematics，Berlin:Springer-Verlag, 2006，pp.366-381.，已被广泛应用于多个领域，如短时交通流量预测(15)商强、杨兆升、李志林，等：《基于相空间重构和RELM的短时交通流量预测》，《华南理工大学学报》(自然科学版)2016年第4期。、机械故障诊断(16)赵书涛、李小双、李大双，等：《基于相空间重构与GSA-LVQ的有载调压变压器分接开关机械故障诊断》，《电测与仪表》,2021年7月2日，https://kns.cnki.net/kcms/detail/23.1202.TH.20210702.0940.002.html，2021年7月3日。等。相空间重构技术与经验模态分解技术相结合可应用于快递业务量预测(17)李辰颖：《基于CEEMD-SVM组合模型的快递业务量预测》，《统计与决策》2019年第12期。、网络流量预测(18)魏臻、陈颖、程磊：《基于VMD-DE的混沌网络流量组合预测研究》，《合肥工业大学学报》(自然科学版) 2019年第12期。、短期风功率预测(19)王贺、胡志坚、陈珍，等：《基于集合经验模态分解和小波神经网络的短期风功率组合预测》，《电工技术学报》 2013年第9期。、溶解氧预测(20)刘晨、李莎、丛孙丽，等：《基于EEMD和萤火虫算法优化SVM的溶解氧预测》，《计算机仿真》2021年第1期。等，这就为更为精确和有效地进行PM2.5浓度的时间序列预测提供了新的思路和方法。

基于以上考虑，本文创新性地采用经验模态分解和相空间重构技术处理复杂的PM2.5浓度时间序列，并据此建立布谷鸟算法优化的支持向量机组合预测模型(EEMD-PSR-CS-SVR)，以提高对未来24小时PM2.5浓度预测的精度和效率。其中，先利用EEMD将PM2.5浓度时间序列模型分解成一组不同尺度且相对稳定的子序列，再通过相空间重构技术对各子序列进行重构得到全新的结构，并进一步在相空间中用布谷鸟算法优化的SVR对各子序列进行预测，最后将各子序列预测结果进行整合得到最终的PM2.5浓度预测结果。实验结果证实所提出的EEMD-PSR-CS-SVR组合预测模型能大幅度提高未来24小时PM2.5浓度预测的准确率。

一、数据来源

本文采用的数据来自北京市环境保护监测中心(http://www.fumenc.com.cn/)发布的北京市亦庄开发区站点的PM2.5浓度(2013年12月5日到2018年12月31日)。由图1可见，PM2.5浓度与气温呈相反趋势，秋冬季节PM2.5浓度水平较高，而春夏季节PM2.5浓度较低，这可能与冬季能源消耗导致的污染物排放量增加有关。为了排除这种季节影响，本文统一选取了此时间段的每年10月份到次年3月份的PM2.5浓度作为研究对象，共937个样本。

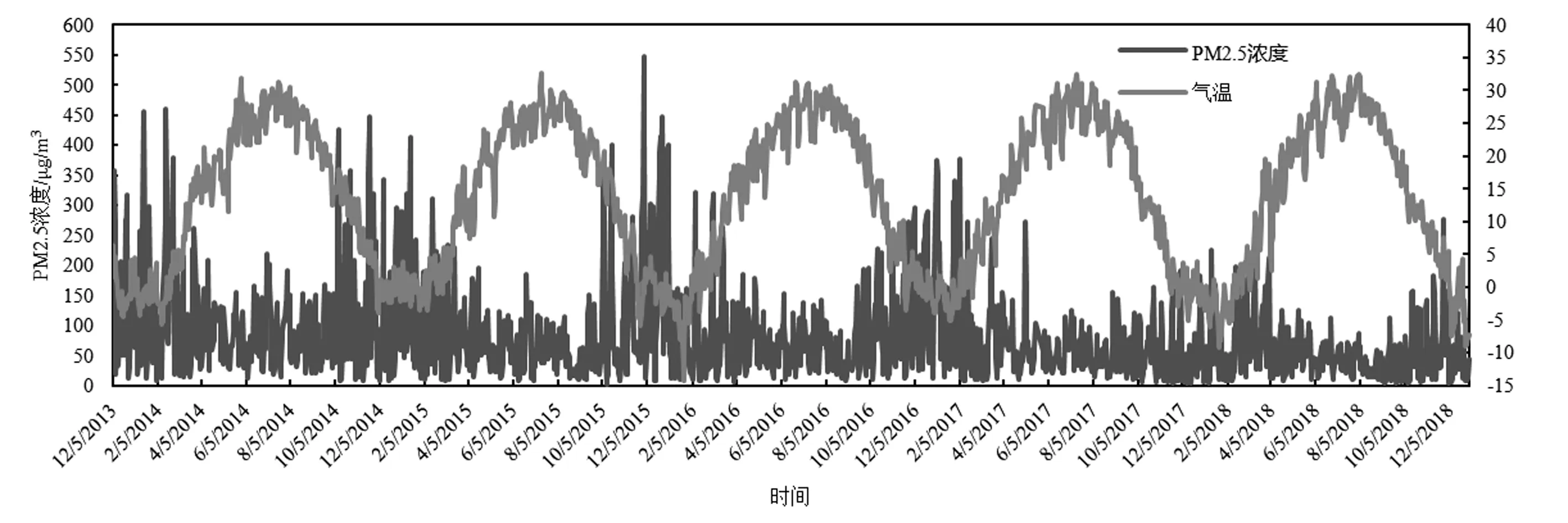
图1 北京市亦庄开发区站点PM2.5浓度与气温(2013年12月5日—2018年12月31日)

二、EEMD-PSR-CS-SVR组合预测模型

(一)集合经验模态分解(EEMD)

Huang等提出的经验模态分解方法(EMD)能够根据信号自身特点，自适应地将非线性、非平稳性的多模态信号分解为一组平稳单一模态的固有模态函数(intrinsic mode function, IMF)分量和一个余项。(21)Huang N.E.,Shen Z.,Long S.R.,et al.,“The empirical mode decomposition method and the Hilbert spectrum for non-stationary time series analysis”，Proceedings of Royal Society of London, vol.454(1998),pp.903-995.但是，传统的EMD方法中IMF分量的不连续会造成相邻波形模态混叠现象，为了弥补这一缺陷，Wu等提出集合经验模态分解方法(EEMD)将白噪声加入待分解信号，补偿分解后IMF所丢失的尺度，然后再进行EMD分解。(22)Wu Z.H.,Huang N.E.,“Ensemble empirical mode decomposition: a noise-assisted data analysis method”，Advances in Adaptive Data Analysis, vol.1,no.1(2009),pp.1-41.EEMD本质就是一种叠加高斯白噪声的多次EMD分解，可利用高斯白噪声频率均匀分布的统计特性，保证模态分解的准确性。(23)赵健、樊彦国、张音：《基于EEMD-BP组合模型的区域海平面变化多尺度预测》，《系统工程理论与实践》2019年第10期。这种方法不仅抵消了加入的白噪声,而且使模态混叠问题在一定程度上得到解决。

EEMD信号分解的具体步骤(24)秦喜文、刘媛媛、王新民，等：《基于整体经验模态分解和支持向量回归的北京市PM2.5预测》，《吉林大学学报》(地球科学版)2016年第2期。：

(1)给待分解信号x(t)中加入一组白噪声ω(t)，构成新的信噪混合体信号X(t)：

X(t)=x(t)+ω(t)

(1)

(2)对X(t)进行EMD分解，使其分解为j个IMF分量和余项：

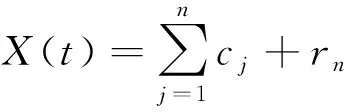
(2)

其中，cj为第j个IMF;n为IMF的个数；rn为余项。

(3)给待分析信号加入多组不同的白噪声ωi(t)：

Xi(t)=x(t)+ωi(t)

(3)

(4)对Xi(t)进行EMD分解，得到不同组的IMF和余项：

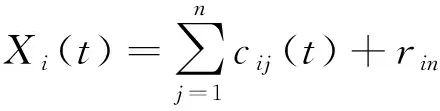
(4)

其中，cij(t)为第i组Xi(t)的第j个IMF；rin为第i组Xi(t)的余项。

(5)将对应的IMF求平均：

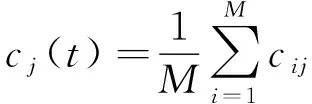
(5)

其中，M为白噪声的数目；cj(t)为对原始信号进行EEMD分解后得到的第j个IMF。

(二)相空间重构(PSR)

相空间重构理论最早由Packard等提出，之后Takens的嵌入理论为其建立了可靠的数学基础，可以将一维混沌时间序列重构成一个多维的时间序列矩阵。(25)孟力、毕叶平：《相空间重构文献综述可视化分析》，《系统仿真学报》2017年第12期。运用此技术进行动力系统重建的关键在于确定时间延迟和嵌入维数，其选取方法有着不同的观点，在本文中分别采用互信息法和虚假邻近点法去求解时间延迟τ和嵌入维数m，从而重构成一个新的多维时间序列(式6)，并在这个重构的相空间中进行后续的分析和预测。

X={xi|i=1,2,…,N}

(6)

其中，m为嵌入维数，τ为时间延迟，M为相点数，M=N-(m-1)τ。

(三)布谷鸟算法优化的支持向量回归预测模型(CS-SVR)

1. 支持向量机回归模型(SVR)

支持向量机算法由Vapnik在20世纪90年代开发(26)Vapnik V., The Nature of Statistical Learning Theory，New York: Springer-Verlag,1995.(27)Vapnik V., Statistical Learning Theory，New York: John Wiley & Sons, 1998.，该算法基于统计学理论并借助于核函数，是解决高纬度数据集分类和回归的有效方法，可以灵活地解决各种非线性问题，已被证实是最稳健和准确的数据挖掘算法之一。

在SVR模型中，训练集为{(xi,yi)|i=1,2,…,n}，其中xi∈Rn为输入变量，yi为因变量，建立一条直线g(x)使其尽可能地接近y，其直线定义为式7：

g(x)=ωTxi+b

(7)

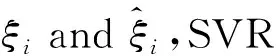
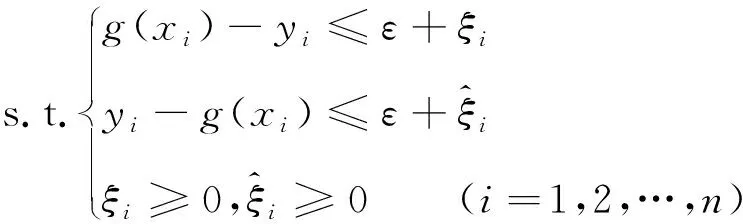
(8)

其中，C为惩罚因子，为待定参数。为了解决以上问题，引入了拉格朗日函数，将其转换为拉格朗日求极值问题：

其中，αi,μi为拉格朗日因子。引进满足Mercer条件的核函数k(xi,x)，将非线性复杂问题转化为高纬度线性问题：

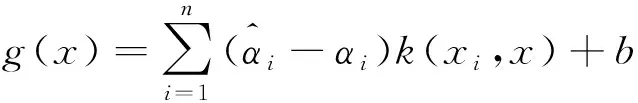
(10)

本文中，采用径向基函数作为核函数：

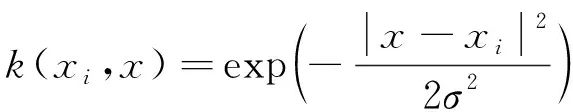
(11)

其中，σ2为待定参数。

2. 布谷鸟算法(CS)

以径向基为核函数的SVR非线性预测模型的性能高度依赖于参数C和σ2，这两个参数的取值通常基于经验，会导致模型预测结果具有随机性和不确定性。因此，采用布谷鸟搜索算法对这两个参数进行优化，能很大程度上提高SVR模型的预测精度和效率。

布谷鸟搜索是Yan and Deb提出的自然启发式算法，它模仿布谷鸟的寄生行为。(28)Yang X. S., Deb S., Cuckoo Search via Lévy flights，World Congress on Nature & Biologically Inspired Computing IEEE, 2010.该算法引入Levy飞行变换位置并遵守三条规则：每只布谷鸟一次只下一个蛋，并将其放入随机选择的巢中；最好的蛋将被带到下一代；可用的宿主巢穴数量是固定的，被宿主发现的概率是Pa∈[0,1]。布谷鸟算法是布谷鸟孵化行为和Levy飞行的结合。在随机形成巢穴种群后，CS通过两条路径更新个体：

(1)布谷鸟采用Levy飞行方式(式12)找到巢并下蛋：

Xt+1=Xt+αS=Xt+α⊗Levy(β)

(12)

Levy(β)～μ=t-β(1≤β≤3)

(13)

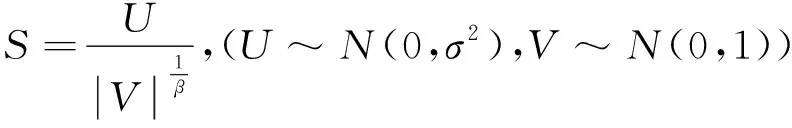
(14)

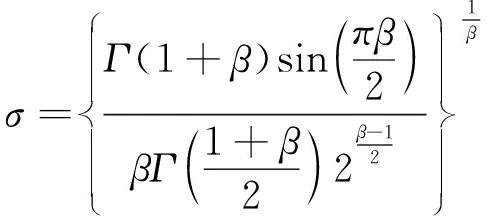
(15)

其中,S是服从Levy分布的随机步长；通常α=0.01，β=1.5。

(2)宿主以概率Pa发现布谷鸟蛋后以随机方式重新建窝：

Xt+1=Xt+γ⊗Heaviside(Pa-ε)⊗(Xi-Xj)

(16)

其中，γ,ε为服从均匀分布的随机数，Heaviside(x) 为跳跃函数，当Pa>ε时，Heaviside(Pa-ε)=1；当Pa<ε时，Heaviside(Pa-ε)=0；当Pa=ε时，Heaviside(Pa-ε)=0.5。Xi,Xj是任意两个鸟窝。Pa=0.25。

CS算法结合了全局和局部搜索，这使得在全局范围内更有效地探索搜索空间成为可能，能以更高的概率实现全局最优。虽然粒子群算法(PSO)可以更早地收敛到局部最优，但不一定是全局最优解，而CS通常可以收敛到全局最优解。

(四)构建EEMD-PSR-CS-SVR组合预测模型

集合模态分解方法(EEMD)能够将非线性的复杂的时间序列分解为一组相对平稳的固有模态函数分量(IMF)，减少模态混叠，保证分解的准确性，再采用相空间重构技术(PSR)对这组固有模态函数分量进行相空间重构，使支持向量机预测模型(SVR)在相空间中进行训练和预测，同时利用布谷鸟算法(CS)在寻找全局最优解方面的优势对支持向量机预测模型的参数进行优化，最后将所有固有模态的预测结果进行结合。针对未来24小时PM2.5浓度预测问题，本文根据以上分解和集合的思想，提出了EEMD-PSR-CS-SVR组合预测模型，其流程如图2所示。

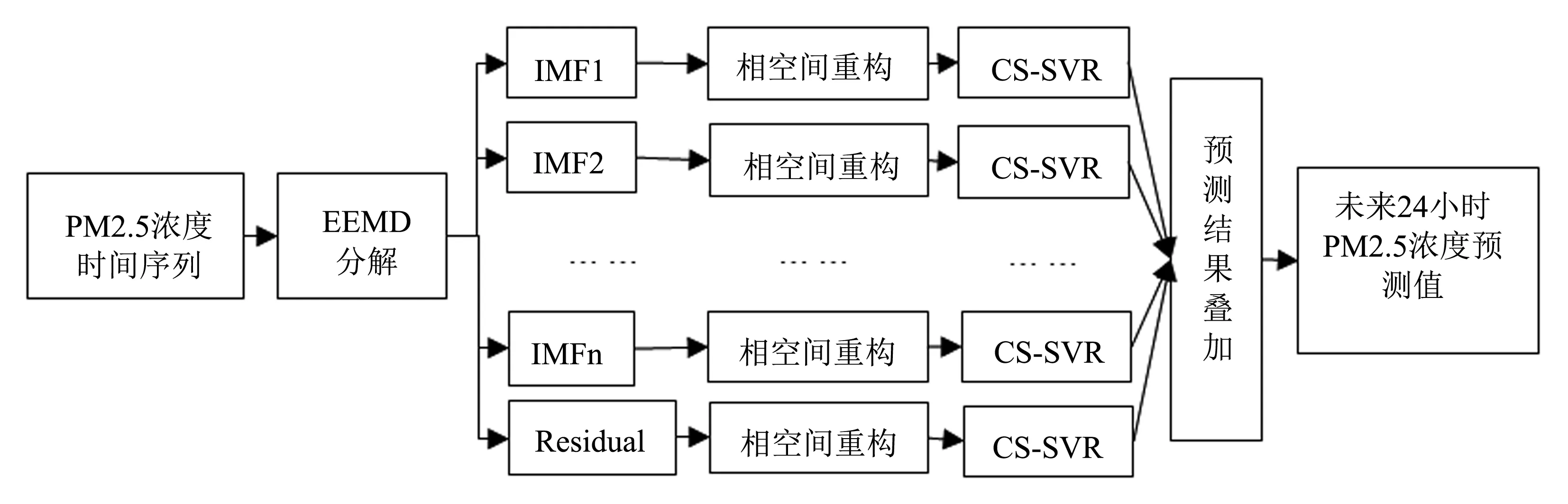
图2 PM2.5浓度EEMD-PSR-CS-SVR组合预测模型流程

(五)评价指标

为了考察EEMD-PSR-CS-SVR组合预测模型的预测精度，并与其他预测模型进行性能的比较，本文采用相关系数(R)、均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)等评价指标对预测结果进行评估:

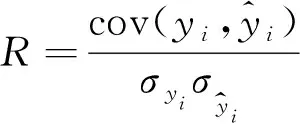
(17)

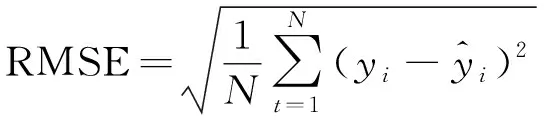
(18)

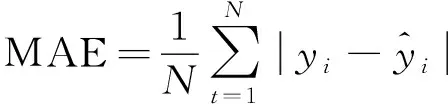
(19)

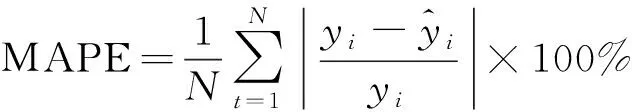
(20)

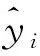
三、模型预测结果与分析

本文采用北京市亦庄开发区观测点2013年12月5日到2018年12月31日冬季PM2.5浓度时间序列作为研究对象，共937个样本数据，其中2018年11月和12月共61个数据作为测试集，剩余876个数据作为训练集，进行单步预测，即使用当日PM2.5浓度的观测值作为模型输入预测未来24小时PM2.5的浓度值，以此重复，得到61个预测值并与观测值进行比较分析。

(一)PM2.5浓度序列EEMD分解

通过对PM2.5浓度的训练集数据进行EEMD模式分解，得到8个固有模态函数(IMF)和1个余项(Residual)。如图3所示，分解出的各个IMF的波动频率从IMF1到IMF8逐渐降低，波动尺度逐渐增大，余项呈现单调递减的趋势。因此，EEMD分解后的子序列复杂度明显低于原始序列，更有利于后续的建模预测与分析。

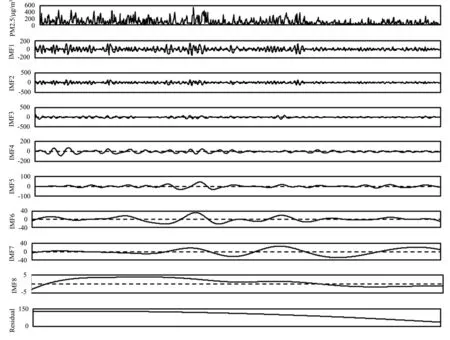
图3 PM2.5浓度时间序列的EEMD分解

(二)子序列的相空间重构

对8个IMF子序列和1个余项进行相空间重构。以IMF4相空间重构过程为例，采用互信息法计算延迟时间τ。如图4所示，当互信息曲线第一次到达最小值时τ=6即为此序列的延迟时间；采用虚假邻近点法计算嵌入维度m=3。式21为IMF4重构后的相空间，并在此相空间中进行模型的训练及预测。全部子序列和余项的时间延迟τ和嵌入维数m如表1所示。

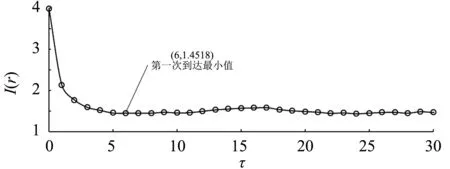
图4 重构延迟时间的确定——互信息曲线(以IMF4为例)

(三)EEMD-PSR-CS-SVR组合模型预测结果与分析

为了验证所提出的EEMD-PSR-CS-SVR组合预测模型的优越性，引入一些目前常用的预测方法作为基准进行对比，主要包括以下三个方面：仅使用单一的预测模型(ARIMA, LSTM, CS-SVR, BP)、使用不同的模态分解方法分解并进行相空间重构后预测(PSR-CS-SVR, CEEMD- PSR-CS-SVR, EMD- PSR-CS-SVR)、使用不同参数优化方法的SVR预测模型(EEMD-PSR-PSO-SVR, EEMD-PSR-CG-SVR)。基于这一系列不同预测模型的未来24小时PM2.5浓度预测结果如图5—7所示。

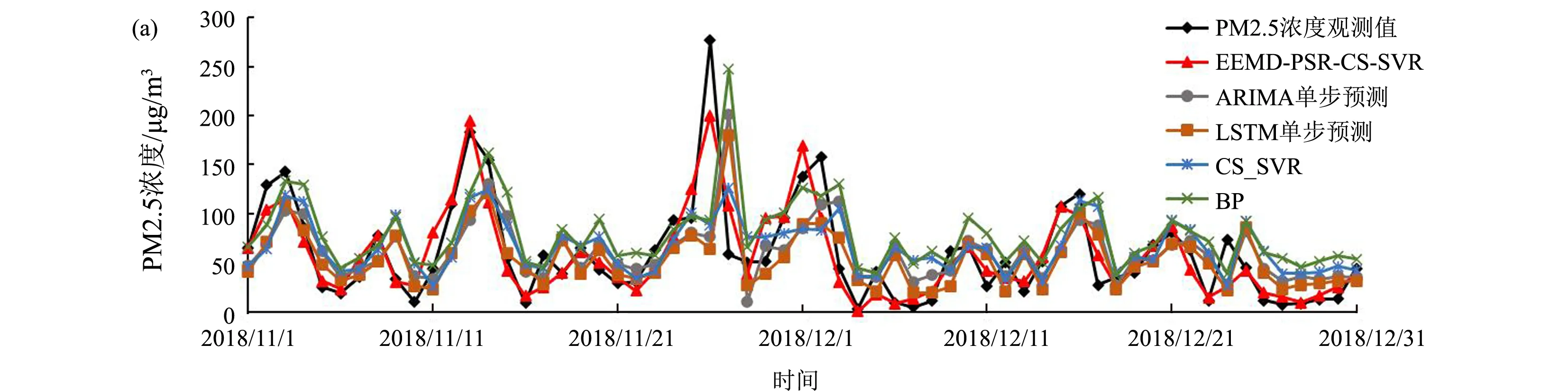
图5 EEMD-PSR-CS-SVR与单一预测模型的预测结果比较

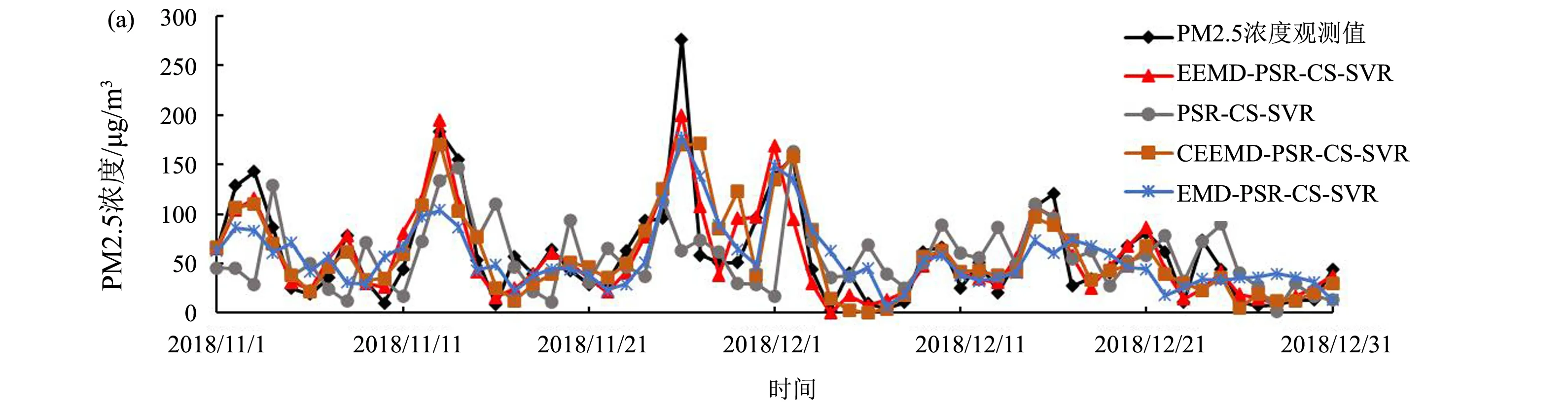
如图5(a)所示，采用单一的预测模型(ARIMA, LSTM, CS-SVR, BP)对未来24小时PM2.5浓度进行预测，所得的预测值与观测值偏离较多，二者的相关系数在0.4523—0.5128之间(表2)，说明拟合度较低。此外，这些单一预测模型的相对误差也远远背离0(图5(b))，表现为MAPE值均大于1，RMSE值在43.9133—50.5085之间，MAE值在31.3935—35.8451之间，这系列误差指标均过大，说明单一预测模型在未来24小时PM2.5浓度预测中具有很大的局限性。为了提高预测精度，引入相空间重构方法对PM2.5浓度时间序列进行预处理后再进行CS-SVR预测(PSR-CS-SVR)，如图6所示，其结果依然不好，预测值与观测值的相关性仅为0.4111。因此，进一步引入模态分解方法，先对数据进行模态分解再对各IMF及余项进行相空间重构(EMD-PSR-CS-SVR, CEEMD-PSR-CS-SVR, EEMD-PSR-CS-SVR)，此时预测精度得到了极大的提升(图7)，预测值与观测值的相关系数提高到0.7112以上，尤其是EEMD-PSR-CS-SVR组合模型的相关系数达到了0.8990，RMSE、MAE、MAPE值分别降低到22.3677，15.5624和0.3874，是预测精度最高的组合模型，说明集合经验模态分解方法和相空间重构技术对于提高模型的预测精度是非常有效的。

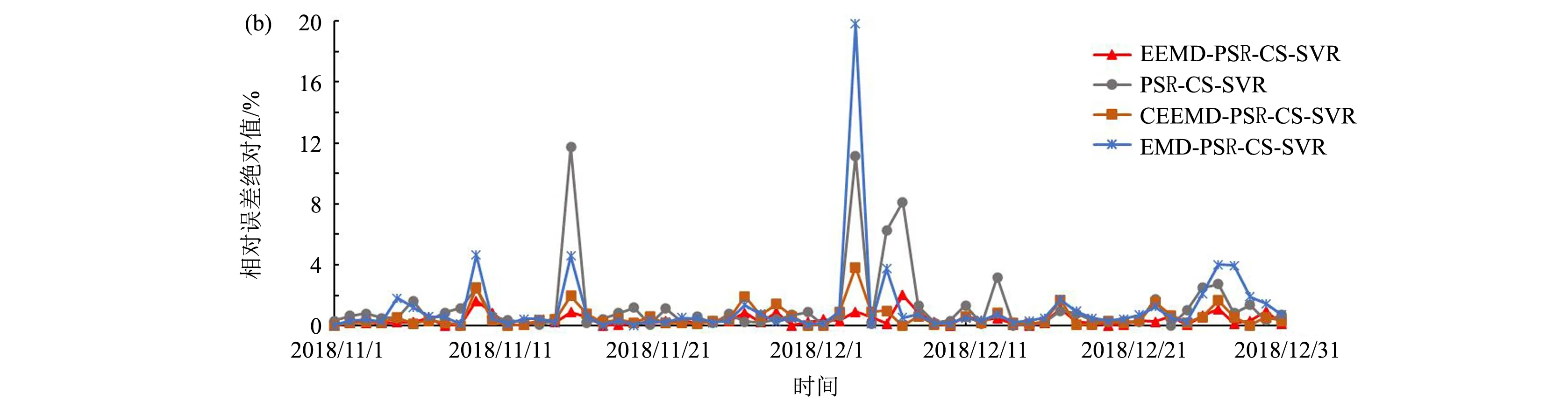
图6 EEMD-PSR-CS-SVR与不同模态分解方法的模型预测结果比较

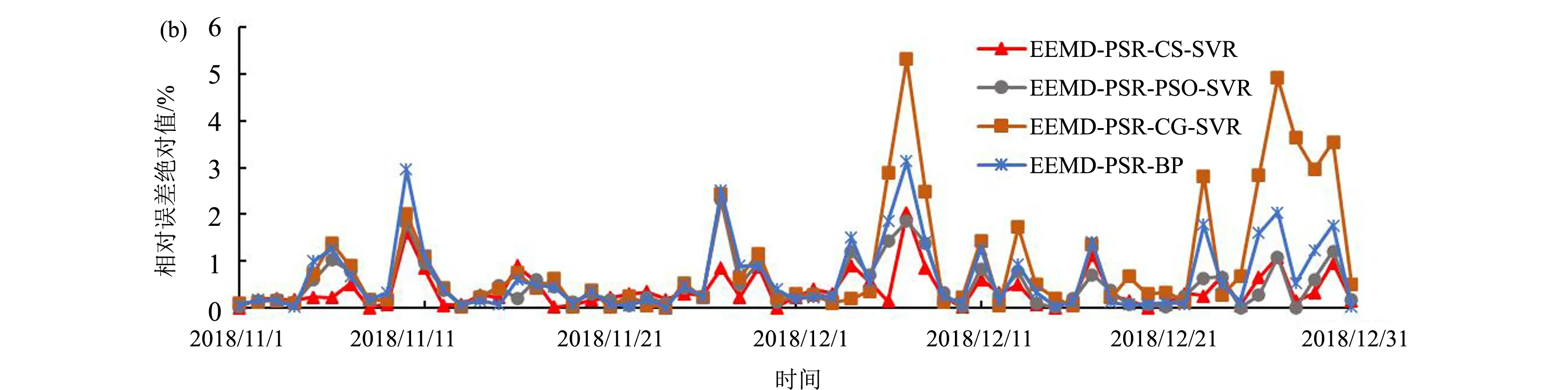
图7 EEMD-PSR-CS-SVR与不同参数优化算法的SVR模型的预测结果比较

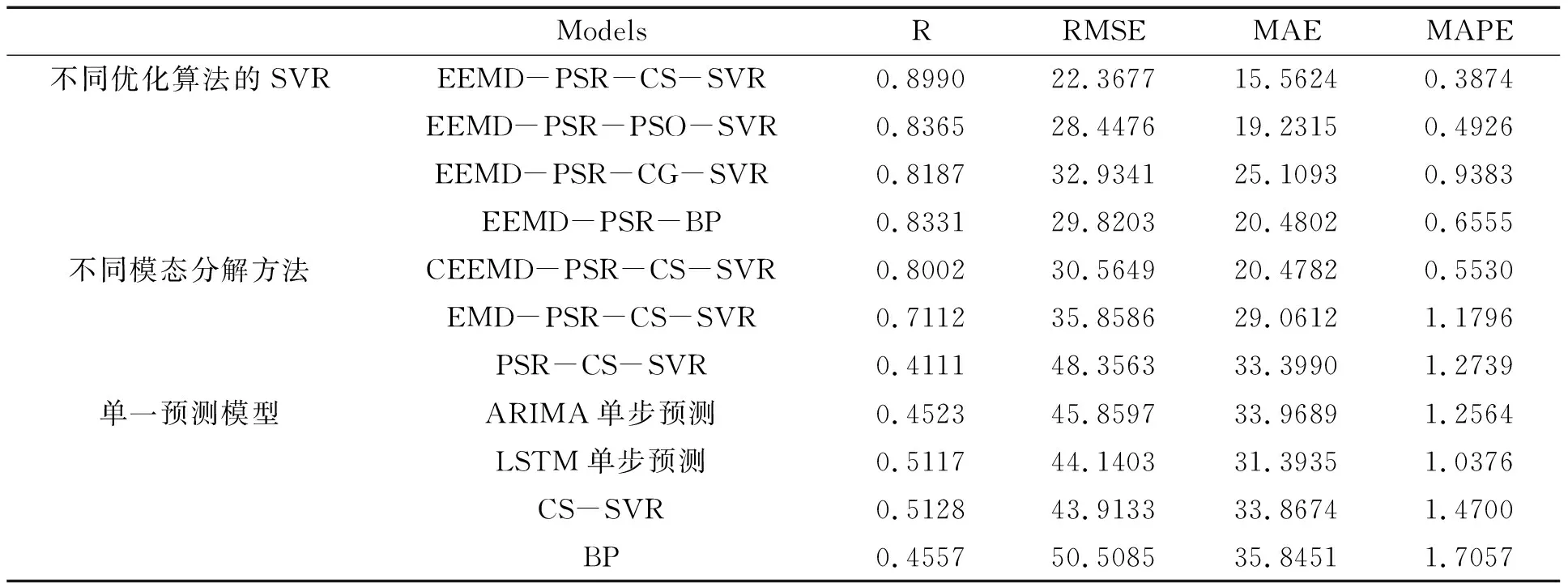
表2 所有预测模型的预测结果评价指标对比

为了进一步验证EEMD-PSR-CS-SVR组合模型的普适性，又将集合经验模态分解方法和相空间重构技术与BP以及不同参数优化算法的SVR进行了结合，得到EEMD-PSR-BP, EEMD-PSR-PSO-SVR, EEMD-PSR-CG-SVR组合模型。如图7所示，这三种组合预测模型的拟合度也均较高，其预测值与观测值的相关系数分别达到0.8331,0.8365和0.8187，且其RMSE、MAE、MAPE值也都有明显降低(表2)，证实了集合经验模态分解方法和相空间重构技术对提高预测精度的普遍有效性。

四、结论

大气中PM2.5浓度受到气象条件、污染物排放等诸多因素的影响，具有非线性的特点，对其进行精确预测极具挑战。针对这一难题，本文提出了基于集合经验模态分解方法和相空间重构技术的PM2.5浓度CS-SVR组合预测模型(EEMD-PSR-CS-SVR)，充分发挥EEMD降低原始时间序列复杂性、PSR可利用有限数据重构原动力系统模型、CS-SVR快速收敛到全局最优以解决非线性问题的优点，获得比传统预测模型精度更高的未来24小时PM2.5浓度预测结果。同时，拓展实验结果证实EEMD-PSR也可以与其他预测模型相组合，提升其预测精度，说明这一策略对未来24小时PM2.5浓度的预测具有较好的普适性。