基于五点插值模型预测控制的车道保持系统研究*

史训昂 吴训成 姚广华 侍 俊

（1.上海工程技术大学机械与汽车工程学院 上海 201620）（2.32128部队 济南 250000）

1 引言

车道保持系统是先进驾驶员辅助系统（ADAS）的关键技术之一，它利用车载传感器实现车辆自动沿预定车道行驶。我们研究了不同控制策略下自动车道保持控制策略的可行性，如直接横摆力偶矩控制（DYC）、动态反馈控制、自适应控制、MPC等［1～3］。

基于多步滚动优化和反馈校正机制，MPC具有良好的控制性能，能够克服模型带来的精度不高的问题。由于如果车辆在接近车辆动力学极限的情况下运行，则非线性预测模型的线性化将在短时间段后变得不那么精确，因此Katriniok等提出了一种LTV（线性时变）-MPC 控制器，该控制器使用连续预测域［4］。Chen BC等提出了一种将自适应模型预测控制与线性时变预测模型结合使用的车道保持系统，其中采用递归最小二乘方法进行实时在线系统识别，以估算出自行车的轮胎转弯刚度模型［5］。Gao，Y 等提出了一种多速率车道保持控制方案，以改善车道保持性能并减少横摆率的波动，并且将横向偏移误差的积分添加到状态反馈控制器中，以改善弯道上的车道保持性能［6］。

本文提出了一种用于车道保持系统的MPC 控制器。通过最小化包含转向角和参考轨迹与预测轨迹之间的误差的代价函数，计算出最优的保持车道控制的转向角指令。此外，通过拟合五个预览点来生成参考轨迹，可以减少对传感器的需求。

2 车辆动力学模型

本文采用线性轮胎模型的简化自行车模型，图1为简化后的自行车模型示意图［7］。

图1 车辆动力学模型

根据牛顿第二运动定律，可以写出车辆横向和车辆坐标系下的横摆运动的平衡方程：

其中m为车辆的质量；Iz为车辆绕Z 轴的转动惯量；φ是车辆的偏航角；δf是前轮的转向角；x为车辆重心（COG）的纵向位移；y为车辆重心（COG）的横向位移；a是COG 到前轴的距离；b是COG 到后桥的距离；Fyf是前轮所受的侧向力，Fyr是后轮所受的侧向力。

当滑移角和滑移比都限制在较小值时，可以将轮胎模型视为线性模型：

其中Caf是前轮的转向刚度系数，Car是后轮的转向刚度系数，前轮滑移角αf和后轮滑移角αr可以由下得到：

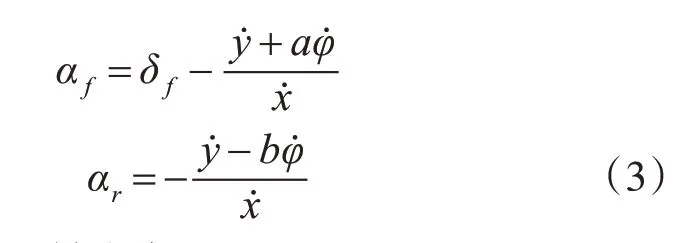
其中δf为前轮的转向角。

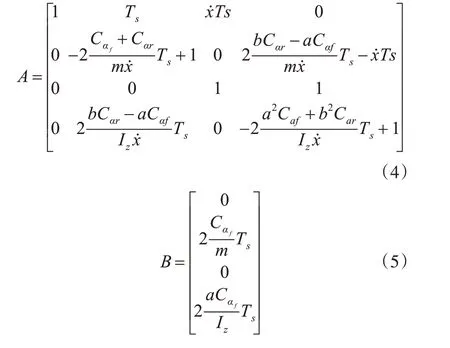
结合式（1）、式（2）、式（3），可将自行车模型写成状态空间形式，用欧拉法离散为

其中x=[y，y˙，φ，φ˙]T，u=δf

3 MPC控制器的控制策略

图2 所示的体系结构描述了使用MPC 来控制前轮转向角的车道保持系统的主要组成部分。仿真环境和被控车辆可以在CarSim 中定义和修改，而车辆状态变量和车辆在五个预览点处的横向位移误差可以通过在CarSim 中设置的传感器得到。通过对5 个预览点的车辆侧移误差进行曲线拟合，可以得到参考轨迹以及当前车辆侧移误差在各预测点的分布情况。其次，针对最优控制问题，研究MPC 控制策略。MPC 控制器用于寻找最佳的前轮转角集合，以最小化参考轨迹和通过横向车辆动力学模型预测的未来车辆轨迹之间的误差。

图2 LKS的控制框架结构

由于模型的输入是控制信号u(k)的控制增量Δu(k)，因此可以推导出增量状态空间模型［8］：

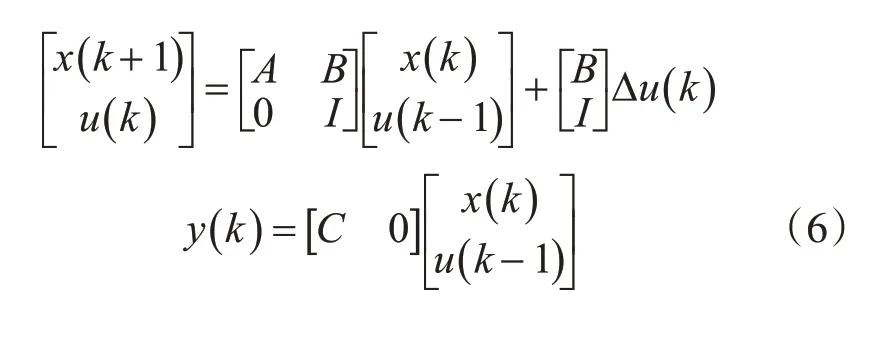
式中C=[1000]T，控制输出y为车辆COG 的横向位移。

式（6）的一般形式如下：

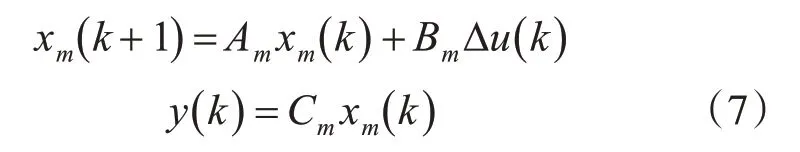
假设在采样时刻k，k＞0，状态变量向量x(k)提供了当前的车辆信息。未来控制序列用Δu(k) ，Δu(k+1)，Δu(k+2)，…，Δu(k+Nc-1) ，其 中Nc称为控制域（control horizon），将未来的状态变量记为xm(k+1)，xm(k+2)，xm(k+3)，xm(k+Np)，Np称为预测域（preview horizon）。一般来说，预测域等于或大于控制域。

定义向量Y和ΔU为

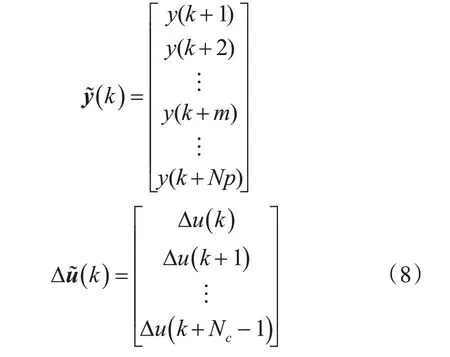
通过推导，未来的预测输出可以表示为

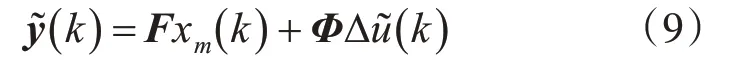
其中：

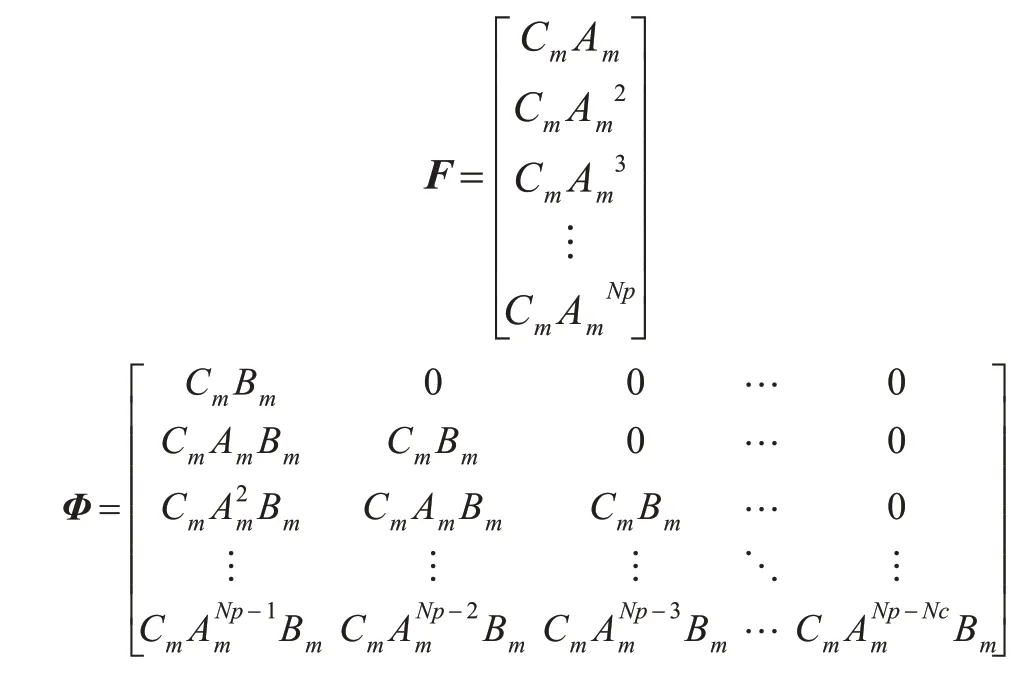
控制器的主要目标是确定控制运动的顺序，以使预测输出与参考轨迹的平方偏差之和最小。目标函数J为

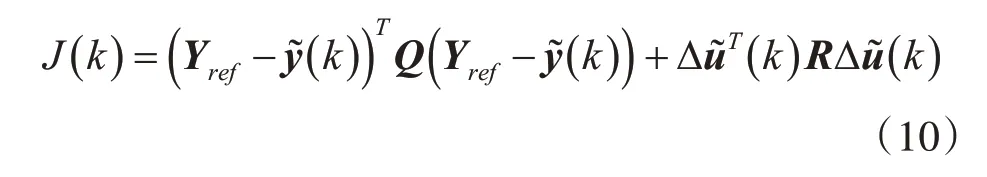
其中Q，R表示权重矩阵，Yref是参考输出。 第一项是使预测输出尽可能接近参考轨迹，而第二项被用来考虑对控制增量Δu的直接限制。

LKS 的参考轨迹图如图3 所示。这五个预览点在预测范围内的距离是由纵向速度决定的。

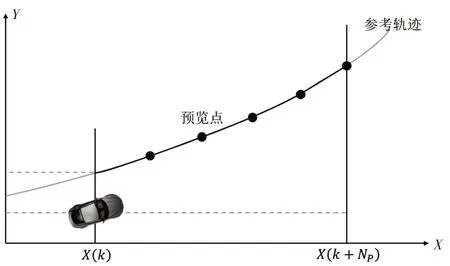
图3 参考轨迹图

用来解决跟踪问题的MPC 控制可以转化为解决已被广泛研究的二次规划（QP）问题，目标函数J可以表示为

其中：

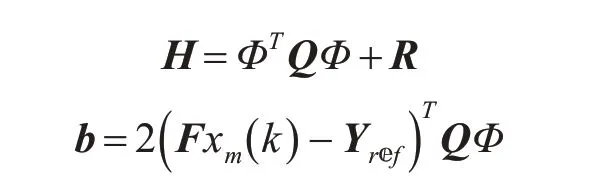
通过式（11），计算得到k时刻的最优转向指令序列为

由于这是一种滚动时域优化策略，因此仅使用此向量Δu*(k)的第一个元素，并在下一个采样时间重复计算。

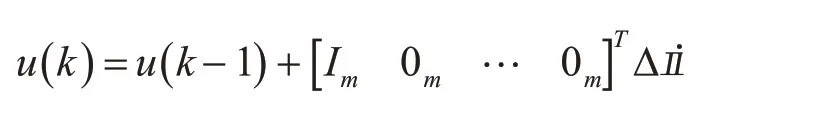
4 仿真实验

本节通过Matlab/Simulink 与CarSim 的联合仿真实验，验证了所提出控制器的有效性。

从仿真结果可以看出，MPC控制器在不同的速度条件下都有很好的性能，其中图5（a）为车辆行驶轨迹，图5（b）为侧向加速度的变化，图5（c）为横摆角速度，图5（d）为车辆四轮转向角度的变化，图5（e）为纵向车速的变化。图5（a）为车辆行驶轨迹，可以明显看出MPC 控制器在仿真过程中的每一个转角跟踪性能都保持良好。从图5（b）、图5（c）可以看出，低速时的偏航率和横向加速度均小于高速时的偏航率和横向加速度，且相对稳定。从图5（d）、图5（e）可以看出，低速情况下车轮转向角表现较好，高速情况下车轮转向角存在一定过大的情况。

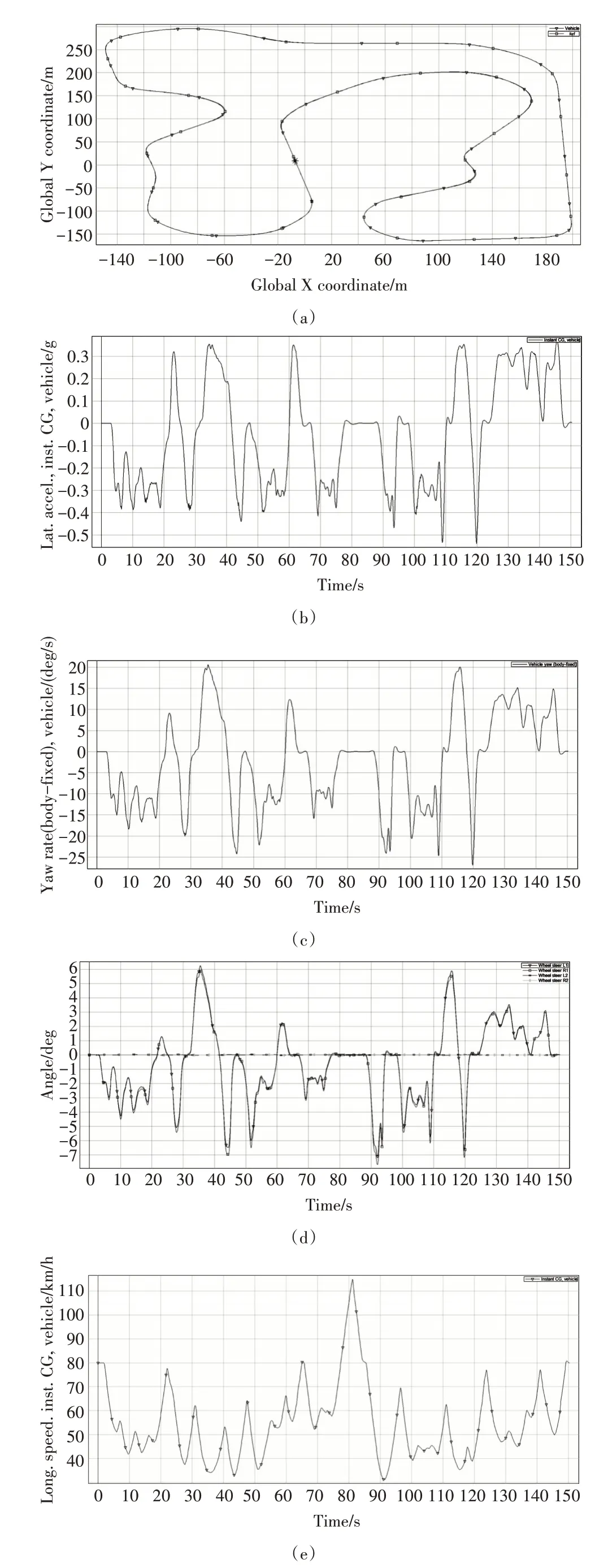
图4 仿真结果

仿真结果表明了该控制器的有效性和鲁棒性，并且该MPC 控制器在低速度下具有更好的跟踪性能和处理性能。

5 结语

本文提出了一种MPC 控制器来实现自动驾驶车辆的车道保持。通过CarSim 和Matlab/Simulink联合仿真方法验证了MPC 算法的性能。基于滚动时域优化和反馈校正的机理，MPC具有良好的控制性能，能够克服模型带来的精度不高的问题。同时，参考输出产生的方法可以降低传感器的要求，这有助于降低研究、开发和生产的成本。