基于haar小波编码和改进K-medoids算法聚合的用户负荷典型区间场景挖掘
2022-06-15许良财邵振国陈飞雄
许良财,邵振国,陈飞雄
(1. 福州大学 电气工程与自动化学院,福建 福州 350108;2. 福建省电器智能化工程技术研究中心,福建 福州 350108)
0 引言
随着电力市场运行机制和辅助服务的快速发展,电力用户逐渐参与电网公司的各项业务。负荷信息作为描述用户用电行为的关键要素,在需求响应的研究中愈发重要[1-2]。用户负荷数据呈现海量、价值密度低的特征,有效挖掘负荷典型场景对于异常用电检测[3]、非侵入式负荷分解[4]、用电套餐设计[5]等需求响应业务均具有重要意义。
负荷典型场景挖掘需要采用聚类技术将负荷样本划分至不同集群,并采用各类集群的特征来表征典型场景,相关研究通常涉及负荷特征提取[6-9]、负荷曲线相似性度量[10-11]、负荷曲线频域分解[12-14]等。
在负荷特征提取方面:文献[6]采用负荷率、日峰谷差率等6 个日负荷物理特性指标进行聚类,并依据聚类有效性修正指标权重;文献[7]利用熵权法为指标赋权,增加负荷极值时间作为新的负荷特性指标,能更准确反映负荷曲线形态特征,有效提升聚类质量;此外,深度学习如长短期记忆网络、卷积神经网络、自编码器等,能够自动提取负荷数据的潜在特征,被广泛应用于负荷聚类[8-9]。
在负荷曲线相似性度量方面:文献[10]利用核函数衡量相似性,提高了负荷样本的可分性;文献[11]结合动态弯曲距离和欧氏距离判断负荷曲线相似性,并利用熵权法配置相似度权重,聚类结果具有较好的鲁棒性。
在负荷曲线频域分解方面:文献[12]利用变分模态分解将负荷样本分解为低频、中频、高频3 个分量,结合低频和中频分量实现负荷的分层聚类;此外,小波变换作为高效的频域分解技术,被广泛应用于提取负荷曲线的不同频域特征,有效提高了负荷曲线的聚类效果[13-14]。
然而,用户不可避免地存在一些非显著用电行为,这导致直接聚类得到的负荷场景典型性不高。同时,目前采用的聚类均值曲线只能描述确定性行为[15],而无法描述负荷在各时段的不确定信息,难以满足负荷不确定性分析需求。
为此,本文提出一种粒度可调的用户负荷典型区间场景挖掘方法。将原始负荷曲线经haar小波变换滤除细节波动分量,提取低维负荷近似序列;分别对负荷近似序列每个维度的特征集进行聚类,提取类簇所包含特征的边界值,将其作为数值区间并进行编码;根据特征占比剔除非显著数值区间,并结合不同维度的显著数值区间得到字符串表征的负荷区间序列;提出一种字符串差异度计算方法,采用改进K-medoids 算法聚合得到负荷区间序列类簇,并提取类簇所包含的负荷近似序列的边界值,从而得到典型区间场景;设置差异度阈值实现典型区间场景的粒度调节,并以爱尔兰某用户实测负荷数据为样本,验证本文所提方法的有效性。
1 负荷区间序列的提取
1.1 负荷归一化
对于某一用户负荷序列P={P1,P2,…,PN},其归一化公式如下:
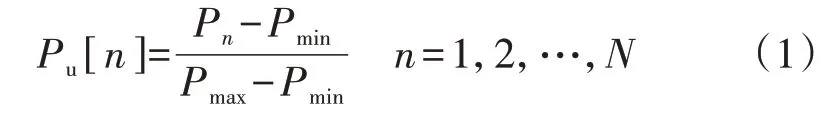
式中:N为用户负荷序列的维度;Pn、Pu[n]分别为归一化前、后第n维度的负荷值;Pmax、Pmin分别为原始负荷最大、最小值。
1.2 基于haar小波变换的负荷近似序列提取
小波变换[13]是一种时序数据分解方法,可以将时序数据分解为1 个反映时序曲线整体变化趋势的近似分量和若干个反映时序曲线细节波动特性的细节分量,小波变换分解示意图如附录A 图A1 所示。图中:A0为初始时序数据;A1和D1分别为第1 层分解的近似分量和细节分量;其他依此类推,下一层分量由上一层近似分量分解得到。
用户负荷典型场景用于反映用户显著的用电行为,可以忽略负荷细节波动特性,而只保留负荷整体变化趋势,因此,本文以小波变换分解得到的负荷曲线近似分量替代原始曲线用于后续聚类分析。本文选用的母小波为haar 小波,分解得到的近似分量为多段水平线,有利于数据降维处理,降低聚类分析的计算复杂度。
采用haar小波变换获取负荷曲线近似分量的公式如下:
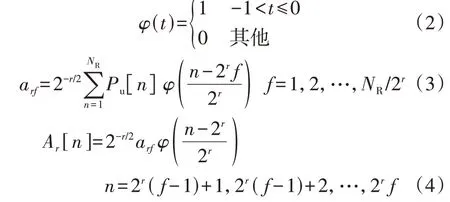
式中:φ(t)为haar 小波函数;r为小波分解层数;arf为第r层负荷曲线近似分量在第f维度的小波近似系数;NR为日负荷序列维度;Ar[n]为第r层负荷曲线近似分量在第n维度的数值。
haar小波变换分解得到的近似分量呈阶梯状变化,图1 为某日负荷曲线及其在不同分解层数的负荷曲线近似分量。需要说明的是,本文每30 min 采样1 次,共得到48 个采样点,对应采样时刻00:30、01:00、…、24:00,后同。
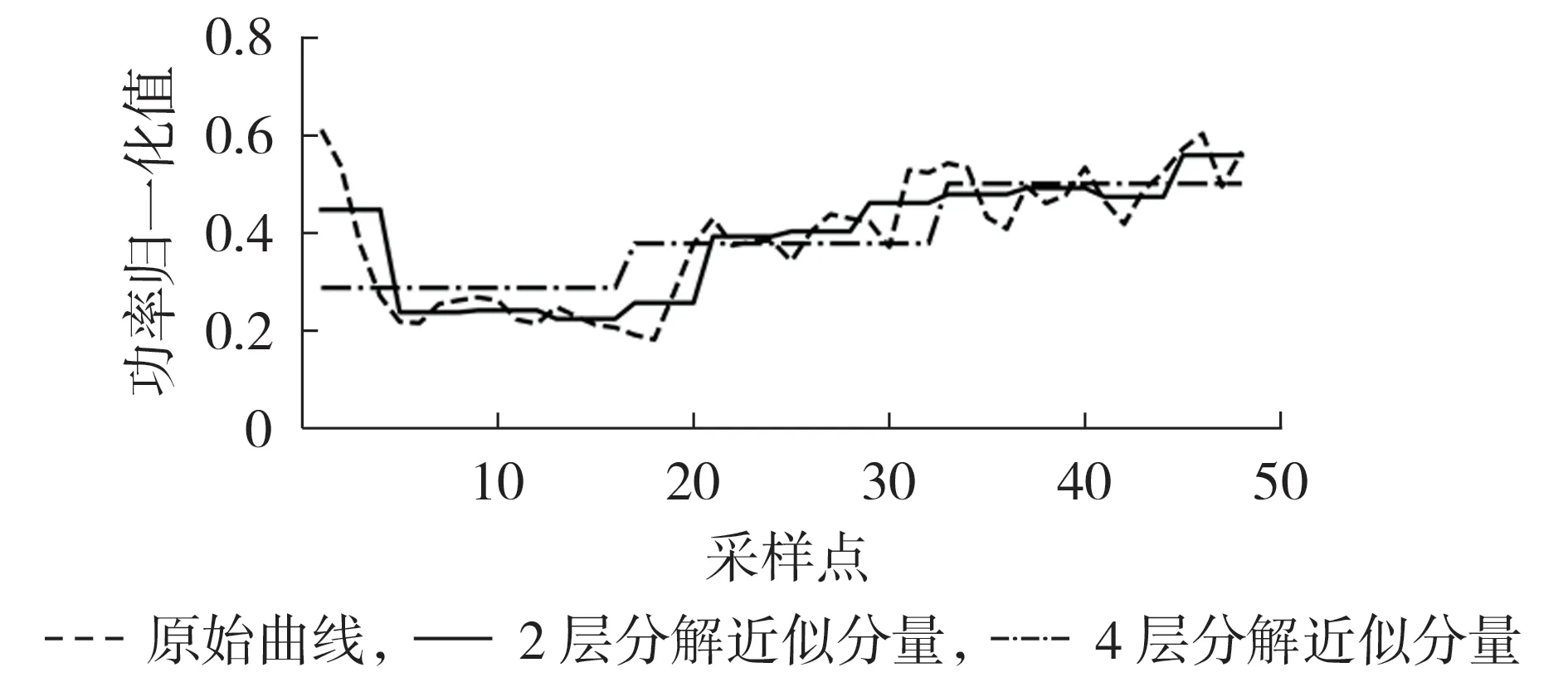
图1 不同分解层数的负荷曲线近似分量Fig.1 Approximate components of load curve for different decomposition layers
由图1 可见,日负荷曲线反映了用户一天中的用电行为变化,在采样频率较高的情况下,日负荷曲线存在显著的细节波动。负荷曲线近似分量由若干段相邻采样时刻负荷数据的均值组成,反映了用户在每一段相邻采样时刻的平均用电水平。当分解层数较小时,近似分量和原始曲线差异较小;当分解层数较大时,近似分量能跟踪原始曲线在较大时间尺度上的变化趋势,但与原始负荷曲线的差异增大。
分解层数为r的负荷曲线近似分量包含M=NR/(2r)段水平线,且每段水平线为对应时段2r个原始负荷数据的均值,因此,可以从中提取M维负荷近似序列表示负荷曲线近似分量。为减少负荷曲线近似分量与原始负荷曲线的差异,同时兼顾聚类分析的计算复杂度,本文选用分解层数为2 的近似分量提取负荷近似序列。
1.3 数值区间编码
本文采用K-means 算法分别对某用户所有负荷近似序列每个维度的特征集进行聚类,提取类簇所包含特征的边界值,得到若干个数值区间,从而描述用户在该维度对应时段的功率分布范围。聚类过程如下。
1)选择聚类数k[m]。不同维度特征集所包含特征的数值分布范围不同,通常数值分布范围越大,划分的类簇越多,因此,以各维度特征的数值分布范围确定聚类数,计算公式如下:
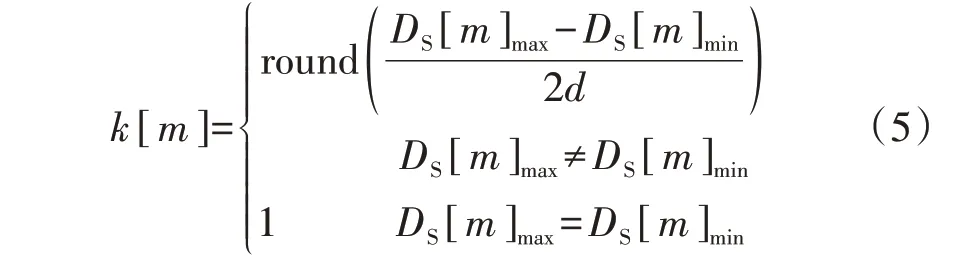
式中:round(·)为向上取整函数;DS[m]max、DS[m]min(m=1,2,…,M)分别为第m维度特征的最大值和最小值,第m维度的所有特征构成集合DS[m]={pm1,pm2,…,pmX},pmx(x=1,2,…,X)为在第m维度特征集中的第x个特征,X为特征集所包含特征数;d为设定的基础数值分布范围值,本文设定为0.1,当特征集的数值分布范围小于2d时,认为所有特征属于同一类。
2)初始化聚类中心。初始聚类中心的选择会影响聚类过程以及最终结果,理论上希望初始聚类中心分布差异越大越好。对于第m维度特征集,本文选取k[m]个特征作为初始聚类中心集C[m]={C1,C2,…,Ck[m]},其中,Ci(i=1,2,…,k[m])为第m维度特征集的第i个初始聚类中心。不同k[m]值的初始聚类中心如附录A 图A2 所示,图中每条线段表示X个特征按照数值从小到大的顺序依次排列。
3)类簇划分。将所有特征按距离最近原则划分至各聚类中心对应的类簇,pmx到Ci的距离dxi为:
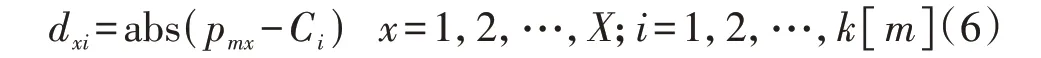
式中:abs(·)为绝对值函数。
4)更新聚类中心。在各类簇中,将各特征的均值作为新的聚类中心,如式(7)所示。
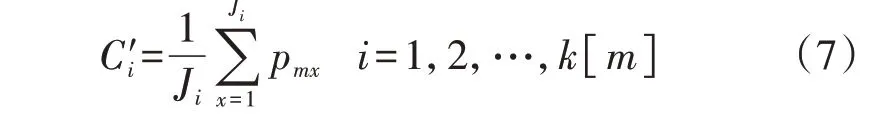
式中:C′i为更新后的第i个聚类中心;Ji为pmx所在类簇的特征数。
5)重复步骤3)、4),直至聚类中心不再发生变化时终止,第m维度的特征集被划分为k[m]个类簇,提取类簇边界值得到k[m]个数值区间。
为了区分不同数值区间,采用字符对数值区间进行编码,使得各时段功率分布范围由若干个字符表征,编码示意图如附录A 图A3 所示,图中负荷近似序列的维度M=12,在每个维度下均存在若干个数值区间,a、b、c表示不同的数值区间。
1.4 非显著数值区间辨识
在附录A 图A3 中,矩形的高度表征数值区间的特征占比,某些特征占比特别低的数值区间可以认为是非显著数值区间并将其剔除。定义特征占比e判别非显著数值区间,公式如下:
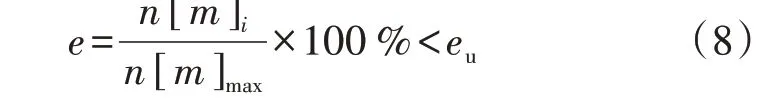
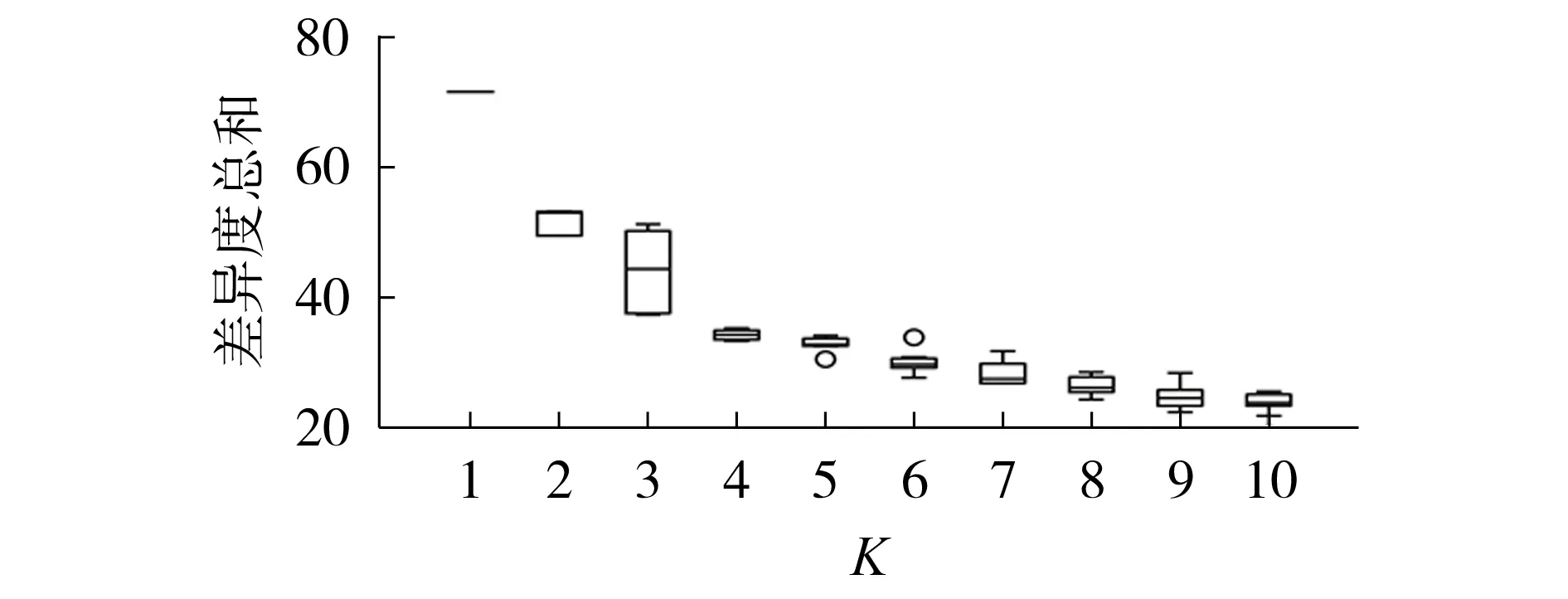
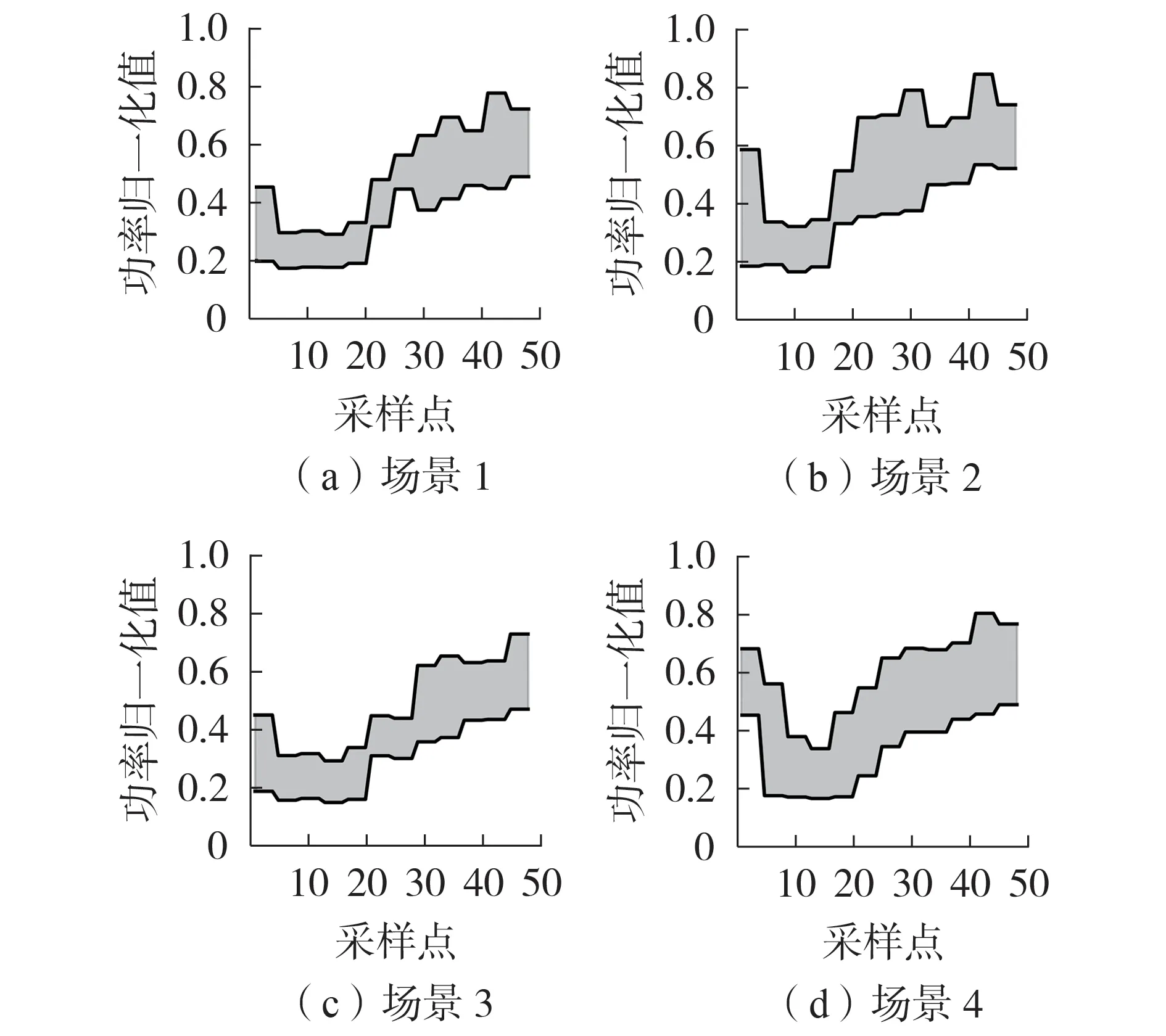
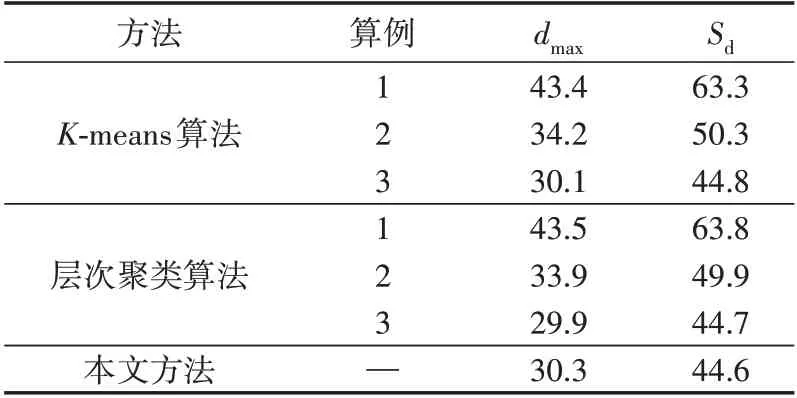
式中:n[m]i为第m维度的第i个数值区间包含的特征数;n[m]max为第m维度的数值区间包含的最大特征数;eu为阈值,本文取为5%。式(8)表示当e 将不同维度的显著数值区间合并,可以得到包含负荷近似序列的负荷区间序列,且每个负荷区间序列由长度为M的字符串表示,某负荷区间序列如附录A图A4所示,字符串表示为“aaaaaaabbbbb”,图中包含了44 个负荷近似序列,如虚线部分所示。进一步提取负荷近似序列的边界值作为负荷区间场景,如附录A 图A5 所示。显然,对于每个负荷区间序列都可以提取一个负荷区间场景,但某些负荷区间序列仅包含1 个负荷近似序列,提取的区间场景为1条曲线,难以涵盖用户多样化的用电行为。 通常字符串差异度采用汉明距离[16]来度量,表现为2 个字符串在对应维度不同的字符数之和。由于本文分别对不同维度的负荷特征集进行聚类,提取数值区间后进行编码,不同维度的字符数不同,且不同字符对应负荷特征类簇的聚类中心也不同,因此,综合考虑上述因素,本文定义一种字符串差异度来衡量不同负荷区间序列的相似性,计算步骤如下。 1)计算各维度的差异度权重因子w1u[m],即: 式中:lk[m]为第m维度的特征集被聚为k[m]个类簇的聚类损失值;l1为第m维度的特征集被聚为1个类簇的聚类损失值;w1[m]为第m维度的特征集由1个类簇聚为k[m]个类簇的聚类损失下降值,该值越大,表示第m维度的特征集被聚为k[m]个类簇时聚类中心与其他特征值的差异越大,理应对应更大的差异度权重因子;w1u[m]为差异度权重因子,是w1[m]的归一化值。特别地,当k[m]=1 时,w1[m]=0,即该维度的特征集只被聚为1 个类簇,差异度权重因子为0。 2)计算类间差异值序列w2u,即: 3)假设w2u[m]h为第i个字符串和第j个字符串在第m维度字符所对应的差异值,计算第i个字符串和第j个字符串的差异度g(yi,yj),即: 式中:yi、yj分别为第i个和第j个字符串。在本文中,采用字符串表征负荷区间序列,因此,g(yi,yj)也表示第i个和第j个负荷区间序列之间的差异度。 以本文定义的字符串差异度来替代传统K-medoids 算法的欧氏距离,对负荷区间序列进行聚合,得到负荷区间序列类簇,过程如下。 1)初始化聚类中心。负荷区间序列集DQ由q个负荷区间序列D1、D2、…、Dq组成,在DQ中随机选取K个负荷区间序列V1、V2、…、VK作为初始聚类中心。 2)类划分。将所有负荷区间序列按照字符串差异度最小划分至不同类簇中,字符串差异度由式(9)—(11)计算得到。 3)更新聚类中心。在各类簇中,计算每个负荷区间序列与当前类簇其他负荷区间序列的差异度之和,并选取差异度之和最小的负荷区间序列作为新的聚类中心,计算公式如下: 式中:gsum为Di与当前类簇其他负荷区间序列的差异度之和;gDij为负荷区间序列Di与Dj的差异度;Oi为Di所在类簇的负荷区间序列数,对应的聚类中心为Vi。 4)重复步骤2)、3),直至聚类中心不再发生变化时终止。 最终,各类簇包含数量不等的负荷区间序列,通过提取各类簇所包含的负荷近似序列的边界值可以得到K个负荷典型区间场景。 由2.2 节的分析可知,采用K-medoids 算法获取典型区间场景需要预先确定聚类数K,为此,本文参照K-means 算法利用手肘法[17]确定聚类数,并提出一种典型区间场景数选取方法,具体如下。 在设置不同K值的条件下,可以计算每个类簇的负荷区间序列与聚类中心的差异度之和,进而得到差异度总和,公式如下: 式中:gCiDj为负荷区间序列Dj与聚类中心Ci的差异度;gall为所有负荷区间序列与对应聚类中心的差异度总和。 差异度总和与传统K-means 算法的误差平方和SSE(Sum of Squares of Errors)类似,其值越小越好,且随着K值的增大,差异度总和呈下降趋势,可以找到差异度总和由急剧减少至平缓减少的拐点来确定合适的K值,在拐点之后,K值增大所导致的差异度总和的减小幅度将显著变小。考虑到不同初始聚类中心会影响聚类结果,本文针对每个聚类数K分别运行50 次并绘制差异度总和的箱线图,如图2所示。在每个箱线图中,箱中横线表示中位数,箱子的上界和下界分别表示上四分位和下四分位。通过对比不同K值的箱中横线可以发现,K值取4是一个合适的拐点,且箱子宽度相对较小,波动程度小,因此,本文设置典型区间场景数为4。 图2 不同K值差异度总和的箱线图Fig.2 Boxplot of sum of differences for different values of K 每个典型区间场景对应一个负荷区间序列类簇,且类簇中的每个负荷区间序列包含数量不等的负荷近似序列。一般而言:典型区间场景包含的负荷近似序列数越多,区间面积越大,越能涵盖用户多样化用电行为,但描述的负荷不确定性也越大,即粒度更粗,不利于精细表征用户用电行为;而典型区间场景包含的负荷近似序列数越少,区间面积越小,越能精细表征用户用电行为,但描述的负荷不确定性也越小,即粒度更细,难以涵盖用户多样化用电行为。为此,在得到负荷区间序列类簇的基础上,本文提出一种典型区间场景的粒度调节方法,步骤为: 1)选取包含负荷近似序列数最多的负荷区间序列作为典型区间序列; 2)根据式(11)计算其余负荷区间序列与典型区间序列的差异度; 3)设置差异度阈值,并剔除与典型区间序列的差异度大于阈值的负荷区间序列; 4)提取剩余负荷区间序列所包含的负荷近似序列的边界值,得到新的典型区间场景。 特别地,为保证挖掘的典型区间场景可以涵盖用户大部分用电行为,本文针对每个典型区间场景分别设置差异度阈值,并依据步骤3)剔除负荷区间序列,即剔除所包含的负荷近似序列,确保经粒度调节后每个典型区间场景包含负荷近似序列的数量占原始数量的85%以上。 本文所提典型区间场景挖掘方法的流程见图3。 图3 典型区间场景挖掘流程Fig.3 Flowchart of typical interval scene mining 为验证本文典型区间场景挖掘方法的有效性,算例分析采用PC机,CPU为Intel(R)Core i7-9750H@2.60 GHz,显卡为Nvidia GeForce GTX 1 650,操作系统为Win10,算法由Python 语言编写,运行平台为Jupyter Notebook。实验数据为爱尔兰地区智能电表实测用户负荷数据[18],选取电表编号为6609的中小型企业用户共536 d的日用电数据。 区间场景的上界和下界分别等于对应区间包含负荷近似序列的最大值和最小值。对于每个区间场景,希望大部分负荷近似序列聚集在区间中部,即序列与区间边界的距离越小越好。此外,较窄的区间场景能更精细地表征用户用电行为,即所有区间场景包含的区域越窄越好。为此,本文定义最大边界距离dmax和典型区域面积Sd评估区间场景的典型性,具体表达式如下: 式中:Bi为第i个典型区间场景包含的负荷近似序列数;quim、qlim分别为第i个典型区间场景在第m维度对应的区间上界和下界;pijm为第i个典型区间场景中所包含的第j个负荷近似序列在第m维度的特征值。 基于3.2 节的用户用电数据,根据式(5)—(7)、(9)可得到各维度的k[m]值和差异度权重因子w1u[m]值,如附录A 表A1所示。当k[m]=1时,该维度的特征样本被归为1 个类簇,对负荷区间序列差异度的贡献度为0,差异值序列w2u为空集;当k[m]=2 时,该维度的特征样本被归为2 个类簇,差异值序列w2u={1};当k[m]=3 时,该维度的特征样本被归为3 个类簇,差异值序列w2u的维数为3,根据式(10)得到计算结果如附录A表A2所示。各维度数值区间编码及包含的特征数如附录A表A3所示。进一步利用式(8)筛选非显著数值区间,如附录A表A4所示。 剔除非显著数值区间后,结合不同维度的显著数值区间得到用户所有负荷区间序列数为278,负荷近似序列数为533,即剔除了3条非显著负荷近似序列。采用改进K-medoids 算法聚合得到4 个负荷区间序列类簇,并提取出4 个典型区间场景,如图4所示,场景1—4 包含的负荷近似序列数分别为81、166、133、153。 图4 采用本文方法挖掘的典型区间场景Fig.4 Typical interval scenes mined by proposed method 由图4 可以看出,4 个典型区间场景的变化趋势相似,在某些时段的功率分布范围存在重叠现象,而在另外一些时段的功率分布范围不同,如:在00:00—02:00 时段(对应采样点1—4),场景4 的功率分布范围为(0.47,0.70)p.u.,明显区别于其余3个场景的功率分布范围;而场景2 的功率分布范围基本包含了场景1 和场景3 的功率分布范围,但在18:00—24:00 时段(对应采样点37—48),场景2 功率分布范围的下限值相对更高,这说明场景2 下该时段的用电水平相对更高;对比场景1 和场景3 可见,在00:00—10:00时段(对应采样点1—20),两者的功率分布范围基本一致,而在10:00—24:00 时段(对应采样点21—48),两者的功率分布范围则存在较大的区别。可见,相较于单一典型曲线描述确定性负荷,典型区间场景能够描述不同时段的功率分布范围,更有助于描述负荷的不确定性。 为了验证本文方法的有效性,分别采用聚类数可选的K-means 算法和层次聚类算法将用户负荷数据集聚为4 类,并提取每类的边界值得到典型区间场景。K-means 算法挖掘得到的典型区间场景如附录A 图A6 所示。层次聚类算法挖掘得到的典型区间场景与K-means 算法挖掘得到的典型区间场景类似,本文不再展示。由图A6可以看出,K-means算法挖掘的典型区间场景存在短暂尖峰现象,不能剔除非典型的细节波动,其中场景2 受非显著负荷影响,区间宽度较大。 为进一步验证haar 小波变换、非显著负荷近似序列剔除能提取更典型的区间场景,分别针对上述2 种聚类算法设计3 个对比算例:算例1,分别采用K-means 算法和层次聚类算法对原始负荷曲线进行聚类得到4 个典型区间场景;算例2,分别采用K-means 算法和层次聚类算法对负荷近似序列进行聚类得到4 个典型区间场景;算例3,首先剔除非显著负荷近似序列,然后分别采用K-means 算法和层次聚类算法对剩余的负荷近似序列进行聚类得到4个典型区间场景。为了便于和本文方法挖掘的区间场景进行比较,算例1—3中均提取类簇包含的负荷近似序列边界值来得到典型区间场景,而不再采用均值负荷曲线来表征用户典型行为。 根据式(14)、(15)计算各算例及本文方法挖掘得到的典型区间场景的最大边界距离和典型区域面积,结果如表1所示。 表1 区间场景的典型性指标对比Table 1 Comparison of typical indicators for interval scenes 由表1 可见,算例1—3 的dmax和Sd逐渐减小,这说明利用haar小波变换提取负荷近似序列以及剔除非显著负荷近似序列可以提升区间场景的典型性。此外,利用本文方法挖掘得到的4 个典型区间场景的dmax和Sd与2 种算法的算例3 结果相当,这说明本文方法通过改进K-medoids 算法聚合得到负荷区间序列类簇,进而提取得到的典型区间场景是有效的。但区别于算例1 对负荷曲线直接聚类以及算例2 和算例3 中频域分解再聚类的方式,本文方法可以实现典型区间场景的粒度调节,通过设置差异度阈值确保4 个典型区间场景包含的负荷近似序列比重都在85%以上,差异度阈值设置与调节结果如附录A表A5 所示。调节后重新计算典型性指标,得到dmax和Sd分别为29.4 和43.2,而未进行粒度调节的典型区间场景的dmax和Sd分别为30.3和44.6,这说明经粒度调节后区间场景典型性得到进一步提升。 针对单一典型曲线描述用户用电行为的不足,本文提出一种基于haar 小波编码和改进K-medoids算法聚合的用户负荷典型区间场景挖掘方法,通过区间形式反映用户在不同时段的功率分布范围,从而更好地描述负荷的不确定性。 采用haar 小波变换提取负荷近似序列,可以忽略负荷细节波动,从而不会因负荷微小波动而增加场景的区间宽度,能更精细地表征用户用电行为。剔除非显著负荷近似序列可以有效减小区间场景所包含的区域面积,提高区间场景的典型性。 设置字符串差异度阈值可以实现典型区间场景的粒度调节,有助于电网公司根据实际需求得到不同粒度的典型区间场景,提高了区间场景的适用性。 通过数据驱动的方式挖掘负荷典型区间场景对数据集质量有较高要求,如要求数据集覆盖全部工况且各工况样本基本均衡等。 附录见本刊网络版(http://www.epae.cn)。2 用户负荷典型区间场景挖掘
2.1 负荷区间序列的差异度
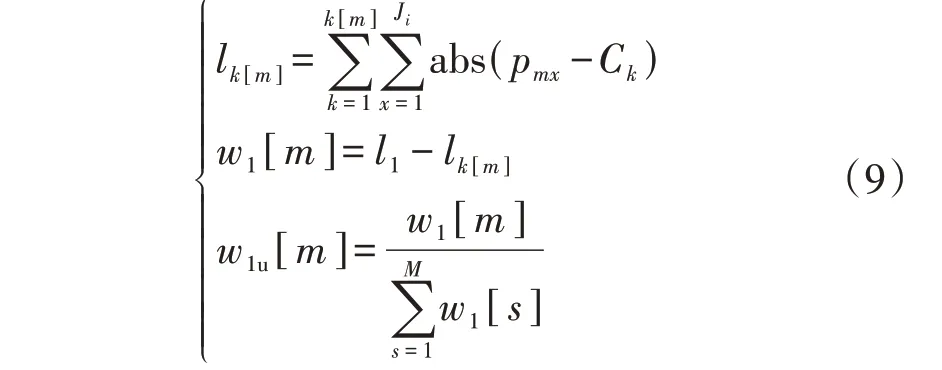
2.2 基于改进K-medoids算法的负荷区间序列聚合
2.3 典型区间场景数的选取
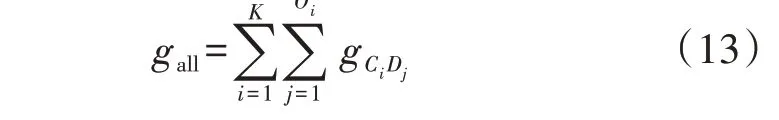
2.4 典型区间场景的粒度调节
3 算例验证与分析
3.1 典型区间场景挖掘流程
3.2 仿真环境设置及实验数据介绍
3.3 典型性指标
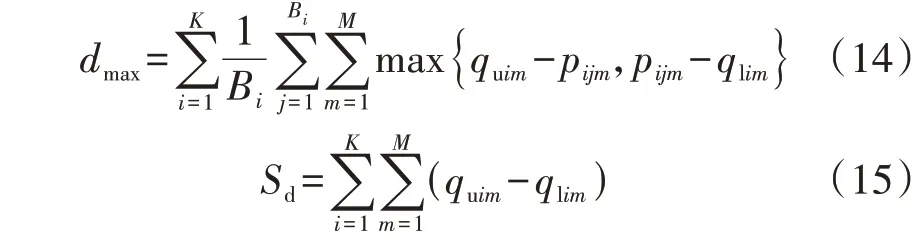
3.4 用户负荷典型区间场景挖掘算例
4 结论
