白鹤滩—江苏特高压混合级联直流系统运行特性分析方法

董芷函，王国腾，徐 政，李建华，丁浩寅

（1. 浙江大学 电气工程学院，浙江 杭州 310027；2. 国家电网华东电力调控中心，上海 200120）

0 引言

目前，基于电网换相换流器（LCC）的特高压直流输电技术（LCC-UHVDC）因具有良好的经济性而被广泛应用［1-2］，但逆变侧LCC 有换相失败的风险。基于模块化多电平换流器（MMC）的特高压柔性直流输电技术（MMC-UHVDC），解决了LCC-UHVDC存在的换相失败、不能接入弱交流系统等问题［3］，但成本相对较高。LCC-MMC 混合直流系统送端整流站为LCC，受端逆变站为采用足够比例全桥子模块的MMC，既降低了成本，又保证了其直流故障处理能力［4］。为进一步降低混合直流系统的成本，逆变站可采用LCC-MMC 混合级联的技术路线［5］。在我国计划建设的白鹤滩—江苏特高压混合级联直流系统中，整流站采用LCC，逆变站由高压阀组LCC 与低压阀组MMC 组串联组成，其中MMC 组由多台MMC 并联组成，构成MMC 并联组（MMCB）。在逆变侧，由于LCC的单向导电性保证了系统具备直流故障清除能力［6］，MMC可以完全采用成本更低的半桥子模块。逆变侧LCC 和MMC 之间的耦合作用使混合级联直流系统呈现出独有的运行特性。为保证白鹤滩—江苏特高压混合级联直流系统投运后的安全稳定运行，需对混合级联直流系统的运行特性进行分析。

针对混合级联直流系统运行特性，前人已经做了很多研究。文献［7］指出，当逆变站中所有换流器接入同一交流母线时，逆变侧交流故障下MMC 存在过电压风险，最严重时MMC 过电压峰值为1.8 p.u.。因此，为保证混合级联直流系统在逆变侧交流故障下可以稳定运行，需要为MMC 高端直流出口配置避雷器，或者将逆变站中不同换流器分散接入交流系统，以降低单一交流故障对直流系统的影响。文献［8］比较了MMC 和LCC-MMC 级联2 种逆变站技术路线下，逆变侧交流故障对直流系统传输能力的影响。结果表明，逆变站采用LCC-MMC级联技术路线时，LCC 换相失败特性导致直流系统在故障期间功率传输能力减弱。根据文献［9］，混合级联直流系统中MMC 配置了旁路开关，如果MMC 交流故障穿越失败导致旁路开关合闸，则MMC 会向直流侧馈入短路电流，造成暂时过电流。文献［10-11］对交直流故障下并联MMC 间直流电流不平衡问题进行了详细研究，并提出了相应的电流均衡控制策略。从前人的研究中可以看出，混合级联直流系统中的MMC 存在暂时过电压风险，不加以抑制还会进一步导致过电流、直流闭锁等问题。

考虑到混合级联直流系统特有的响应特性，混合级联直流系统的接入势必会给电网带来新的安全稳定问题。分析直流系统运行特性对保证电网安全稳定运行至关重要。对于常规直流，已有成熟的分析方法，并且在实际工程中得到了验证［12］。近年来，随着柔性直流系统的应用，学者们提出了多种考虑柔性直流系统馈入的电网运行特性分析方法［13-14］。文献［15］针对混合多馈入交直流混联系统，提出了中长期电压稳定分析与控制方法。文献［16］提出了一种广义短路比，以评估各类电力电子装置馈入系统的电压稳定性。混合级联直流系统是一种采用新型拓扑结构的直流系统，该系统的运行特性分析方法还有待进一步研究。

本文首先介绍了混合级联直流系统拓扑结构和数学模型；然后提出一种混合级联直流系统运行特性分析方法，该方法综合考虑了混合级联直流系统稳态响应特性、逆变侧LCC 换流母线电压稳定性、MMC 暂时过电压估算以及逆变站出线热稳裕度计算4 个方面；接着利用所提分析方法对白鹤滩—江苏特高压混合级联直流系统运行特性进行分析。

1 混合级联直流系统数学模型

混合级联直流输电系统的拓扑结构见图1。整流站采用LCC，逆变侧由高压侧LCC与低压侧MMCB串联而成。每台换流器可以接入不同交流母线。

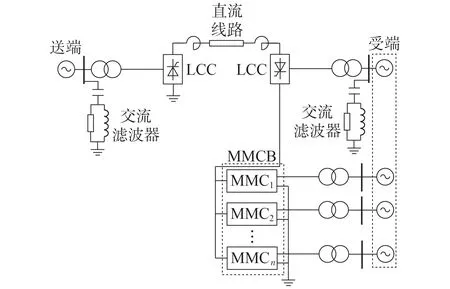
图1 混合级联直流系统拓扑Fig.1 Topology of hybrid cascaded DC system

整流侧LCC数学模型可用微分代数方程描述为：

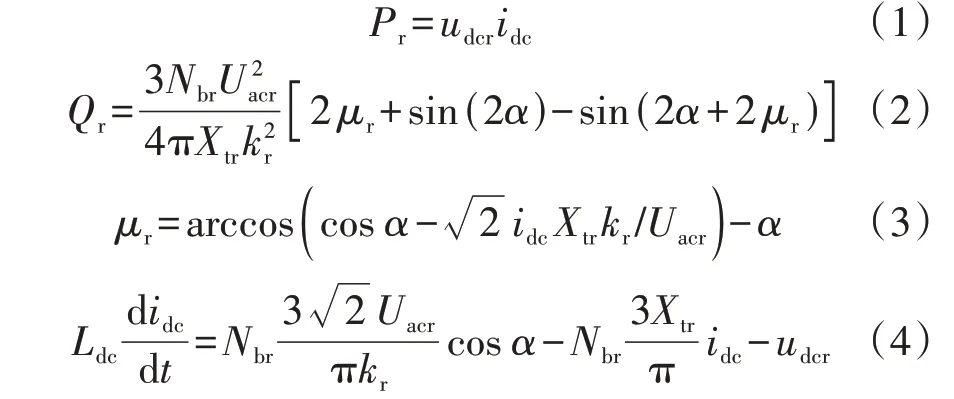
式中：Pr和Qr分别为整流侧LCC 的有功和无功功率；udcr和idc分别为整流侧LCC 的直流电压和直流电流；Uacr为整流侧换流母线的线电压有效值；kr与Xtr分别为整流侧换流变压器的变比与漏抗；Nbr为整流侧LCC 的6 脉波桥个数；α和μr分别为整流侧LCC 的延迟触发角以及换相重叠角；Ldc为平波电抗器的电感。

对于直流线路有：

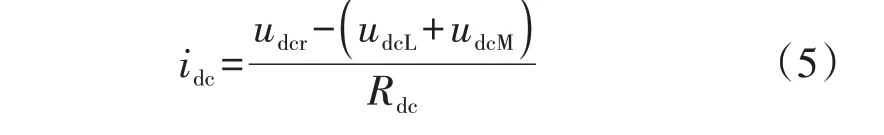
式 中：udcL为 逆 变 侧LCC 直 流 电 压；udcM为 逆 变 侧MMC直流电压；Rdc为直流线路电阻。

逆变侧LCC 的数学模型与整流侧LCC 基本相同，这里不再复述。本文中MMC 数学模型采用文献［17］提出的机电暂态模型。MMC 机电暂态模型的直流侧为等效电容Ceq并联一个受控直流源，而交流侧被等效为注入电流源与电感的串联结构，如附录A 图A1 所示。对于MMCk（k=1，2，…，n），其数学模型的表达式见式（6）—（8）。

式中：idcMk为流入MMCk的直流电流；idcsk为受控直流源的电流值；PMMCk为MMCk交流侧流出的有功功率；usd、usq分别为MMC 所接交流母线电压的d、q轴分量，isd、isq分别为MMC 交流电流的d、q轴分量，其大小分别由MMC的内、外环控制器决定。

对于混合级联直流系统，逆变站换流器交流侧模型均独立，直流侧通过串并联耦合。因此，混合级联直流系统的直流侧等效电路如附录A 图A2所示。本文中整流侧LCC 采用定直流电流控制，配置低压限流环节（VDCOL）和最小触发角限制。逆变侧LCC采用定关断角控制，附加后备定直流电流控制，并配有VDCOL。MMC 采用电流矢量控制，其有功控制模式为其中1 台MMC 采用定直流电压控制，其余MMC 采用定有功功率控制，无功控制模式为所有MMC均采用定无功功率控制。

2 混合级联直流系统运行特性分析方法

下面提出一种混合级联直流系统运行特性分析方法，该分析方法主要由4 个部分构成：1）混合级联直流系统稳态响应特性分析；2）逆变侧LCC 换流母线电压稳定性评估；3）MMC 暂时过电压估算方法；4）逆变站出线热稳裕度评估。

2.1 混合级联直流系统稳态响应特性分析

为了得到混合级联直流系统中控制器的稳态响应特性，本文采用逐步降低换流母线电压的方法来测试控制器的响应特性。对于混合级联直流系统，整流侧LCC集中接入同一交流母线。要想获得整流侧LCC换流母线电压跌落时混合级联直流系统响应特性，保证逆变侧换流母线电压不变，采取逐步降低整流侧LCC换流母线电压的方式即可。

混合级联直流系统逆变站中多台换流器通常接入同一电网中的不同交流母线。受端电网某换流母线电压降低时，其余换流母线电压也会发生变化。因此，要想获得逆变侧换流母线电压跌落时直流系统响应特性，需要获得受端电网详细信息。为此，本文对混合级联直流系统逆变侧做如下处理：

1）完全保留受端电网网架结构，以保证换流母线间的电气距离与实际情况相符；

2）将电网中所有发电机等效为戴维南等值电路，以保证系统强度与实际情况相符，戴维南等值电路中阻抗为发电机次暂态电抗，电动势为发电机的次暂态电动势。

通过上述处理，可以在保证交流系统强度、换流母线之间电气距离不变的前提下获得混合级联直流系统在逆变侧换流母线电压跌落时的响应特性。

2.2 逆变侧LCC换流母线电压稳定性评估

逆变侧LCC换流母线电压稳定性可以分为静态电压稳定性和暂态电压稳定性2 类。对于换流母线的静态电压稳定性，本文采用电压稳定系数λVSF［18］来评估。对于逆变侧LCC 换流母线的电压稳定系数，这里将其定义为：

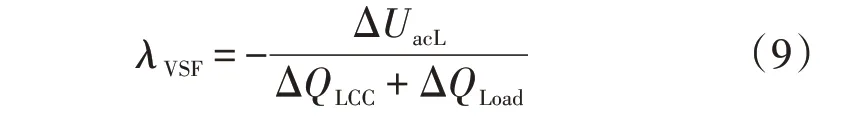
式中：ΔUacL为逆变侧LCC 换流母线的电压变化量；ΔQLoad为换流母线处无功负荷的变化量；ΔQLCC为LCC 吸收无功功率的变化量。具体求取方法是在换流母线处施加一个无功负荷扰动ΔQLoad，通过仿真计算得到逆变侧LCC吸收无功功率的变化量以及换流母线电压的变化量ΔUacL。当λVSF>0 时，换流母线为静态电压稳定；当λVSF≤0时，换流母线电压不稳定。

对于换流母线的暂态电压稳定，本文采用短路故障切除瞬间母线电压跃升水平Up来评估。获取方式是在换流母线处施加三相金属性接地短路故障，故障切除瞬间换流母线电压数值即为Up。Up数值越小，直流系统无法恢复的风险越高。

2.3 MMC暂时过电压估算方法

根据前人的研究，混合级联直流系统在受端电网短路故障下会出现暂时过电压问题［7］。为此，本文提出一种MMC 暂时过电压估算方法，以评估MMC 可能出现的最大过电压水平。受端电网短路故障下MMC暂时过电压有以下特点：

1）定直流电压控制的MMC 出口处三相金属性接地短路故障造成的暂时过电压最大，所以在估算MMC 可能出现的最大暂时过电压时，只考虑定直流电压MMC出口处的三相金属性接地短路故障［19］；

2）短路故障清除后MMC 直流电压基本不会继续升高，峰值在故障清除时刻出现［8］；

3）逆变侧LCC 未发生换相失败时，根据控制方式不同，其直流电压udcL或关断角γ通常可以控制在额定值附近［1］。

考虑混合级联直流系统中有n台MMC 并联，则MMC直流电压的微分方程为：

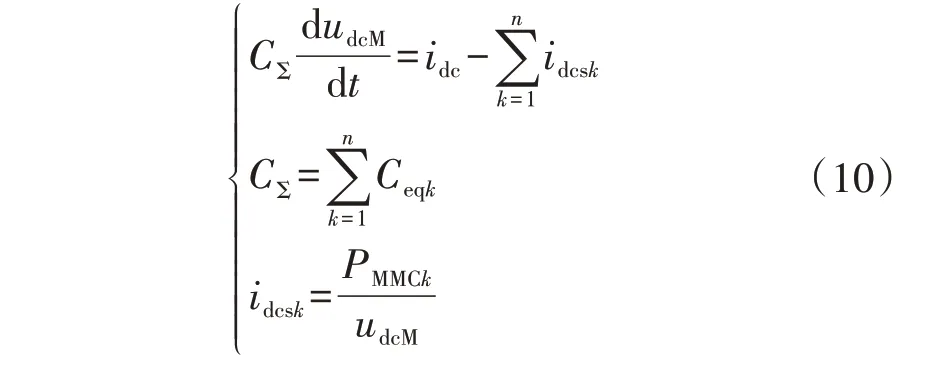
进一步，式（10）可以变换成式（11）。

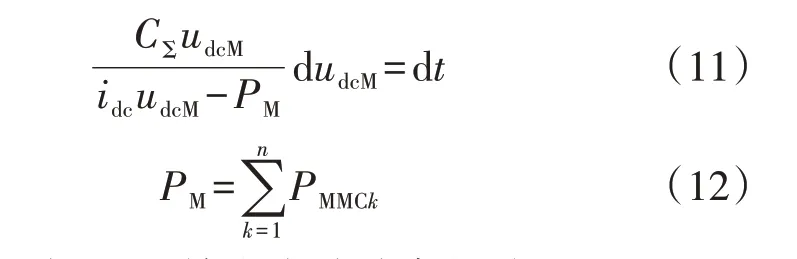
式中：PM为所有MMC输出有功功率的总和。

对式（11）等式两边同时积分可以得到式（13）。

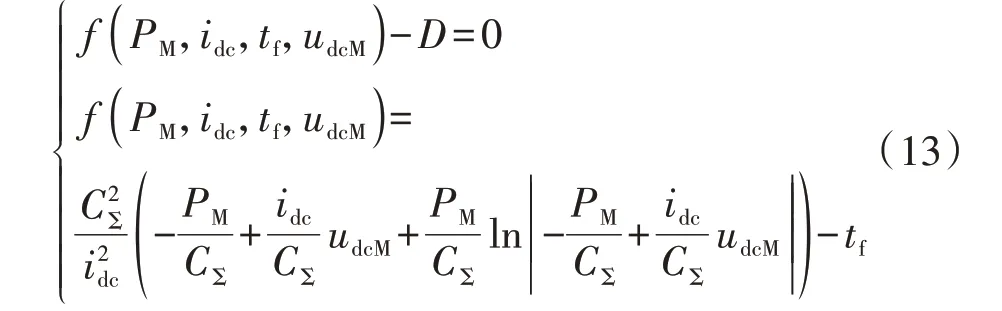
式中：tf为故障持续时间；D为常数，将故障发生时刻作为初始时刻，可以根据系统初始条件求得该常数。

在已知MMC输出有功功率PM、直流电流idc以及故障持续时间tf的情况下，代入式（13）即可求得故障切除时刻MMC 的直流电压。考虑继电保护动作和断路器跳开所需时间，在安全稳定计算当中，故障持续时间tf通常选取固定时间100 ms。下面分步介绍如何获取MMC输出有功功率PM和直流电流idc。

1）步骤1：计算定直流电压控制MMC 出口发生三相金属性接地短路故障时，其他MMC 和级联LCC出口处的交流母线电压。电压估算方法是利用多馈入交互因子ξMIIF，通过式（14）进行计算。

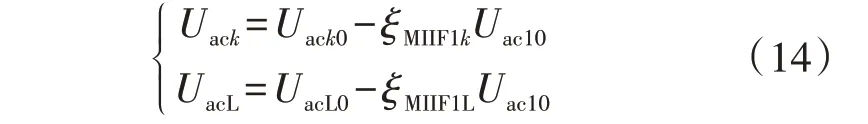
式中：Uack为待求定有功功率MMCk换流母线电压；UacL为待求级联LCC 换流母线电压；Uack0、UacL0分别为待求MMCk、LCC 换流母线电压初始值；Uac10为定直流电压MMC 换流母线电压初始值，由于该母线发生三相金属性接地短路故障，Uac10也是变化量；ξMIIF1k、ξMIIF1L分别为定直流电压MMCk与其他MMC、级联LCC 间的多馈入交互因子，其定义及计算方法参见文献［20］。

2）步骤2：计算定有功功率MMC 输出有功功率PMMC。当1台定有功功率控制MMC 输出交流电流未达到上限时，该MMC 交流侧输出功率即为参考值。若MMC 换流母线电压跌幅过大，使得MMC 输出电流达到上限的情况下依然不能输出指定有功功率，则应按照MMC 可输出最大电流重新计算有功功率。电压跌落后MMC的有功功率计算表达式为式（15）。

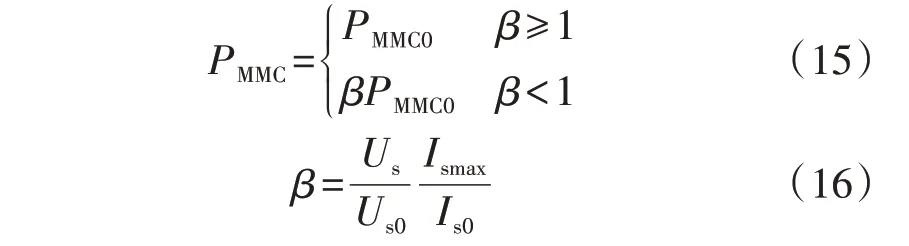
式中：PMMC0、PMMC和Us0、Us分别为换流母线电压跌落前、后MMC 输出有功功率和电压值；Ismax为MMC 可输出最大电流限幅值；Is0为MMC 在换流母线电压跌落前MMC输出电流幅值。

3）步骤3：计算逆变侧LCC 直流电压。根据逆变侧LCC 换流母线电压，判断逆变侧LCC 是否发生换相失败。这里对逆变侧LCC是否发生换相失败的判据沿用PSS／E 中CDC6T 直流模型的换相失败判据，即逆变侧LCC 换流母线电压小于某一阈值时判定逆变侧LCC发生换相失败。若逆变侧LCC发生换相失败，则故障期间逆变侧LCC 的直流电压为0。若逆变侧LCC 没有发生换相失败，则根据控制方式计算直流电压：如果逆变侧LCC 采用定直流电压控制，则短路故障发生后逆变侧LCC 直流电压保持不变；如果逆变侧LCC 采用定关断角控制，则按照式（17）重新计算直流电压。

式中：Nbi为逆变侧LCC 的6 脉波桥个数；Uaci为逆变侧换流母线的线电压有效值；ki和Xti分别为逆变侧换流变压器的变比和漏抗；μi为逆变侧LCC 的换相角，其满足式（18）。

4）步骤4：计算造成逆变侧LCC 后备定电流控制投入所需故障持续时间。需要注意的是，随着MMC 直流电压的增长，idc并不是一直保持恒定不变的。在整流侧LCC 触发角α未达到最小限制之前，直流电流被整流侧LCC控制在额定值。但是整流侧LCC 达到最小触发角限制后，逆变侧LCC 后备定电流控制投入，直流电流由逆变侧LCC 控制在额定值的90%。故获取MMC过电压峰值之前，需要知道故障期间逆变侧LCC的后备定电流控制是否会投入。考虑控制方式切换的临界状态，即整流侧LCC达到最小触发角限制，且逆变侧LCC 的后备定电流尚未投入。在已知整流侧交流母线电压、直流电流以及逆变侧LCC 直流电压的情况下，可求得造成控制方式切换的MMC直流电压ucm，如式（19）所示。

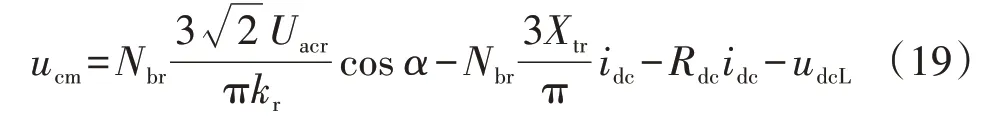
根据步骤2 求得的MMC 输出有功功率，取直流电流为恒定值，取MMC 的直流电压为ucm，代入式（13），即可得到造成逆变侧LCC 后备定电流控制投入所需的故障持续时间，这里用tg表示。

5）步骤5：计算MMC 暂时过电压峰值。如果tg大于实际故障持续时间tf，则说明故障持续期间没有控制方式切换，直流电流由整流侧LCC 控制在额定值，根据式（13）直接求解暂时过电压峰值即可。如果tg小于等于实际故障持续时间tf，则需要分2 段计算MMC 过电压峰值：第一段是故障自发生起持续tg期间，在该时间段内，直流电流由整流侧LCC控制在额定值，根据式（13）可求得第一段结束时MMC 直流电压；第二段是故障持续tg后到故障结束期间，时长为tf-tg，在该时间段内，直流电流由逆变侧LCC 后备定电流控制决定。将第一段终值作为第二段计算的初值，在式（13）中更新第二段计算所需的常数D，代入后备电流指令值和故障持续时间tf即可得到最终的MMC暂时过电压峰值。

MMC 暂时过电压估算方法的流程图如附录A图A3 所示。该估算方法的输入为定直流电压MMC与LCC之间的多馈入交互因子以及定直流电压MMC与其他MMC 之间的电压交互因子，输出为MMC 直流电压峰值。

2.4 逆变站出线热稳裕度评估

针对直流系统中的任意一台换流器，逐步增加该换流器的出力并计算系统潮流，当其出线中任意一回达到热稳定功率极限时，该换流器出力达到热稳极限。MMCk出线的热稳裕度λk和级联LCC 出线的热稳裕度λL分别为：

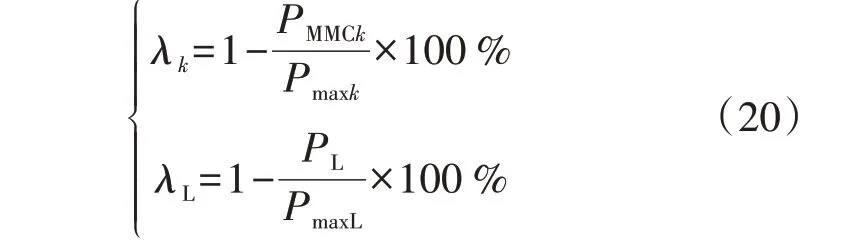
式中：Pmaxk与PmaxL分别为MMCk与级联LCC 出力热稳极 限；PMMCk与PL分 别 为MMCk与 级 联LCC 的 实 际出力。

混合级联直流系统的逆变侧由多台换流器串并联组成，并且每台换流器接在不同交流母线上。因此，每台换流器的出线热稳裕度都不同，对于该直流系统，本文将所有换流器出线热稳裕度的最小值作为最终的换流站出线热稳裕度，如式（21）所示。

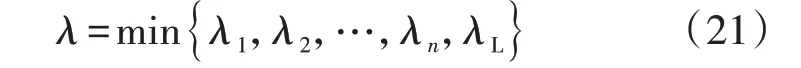
另外，需要注意的是，并联MMC 之间具有功率互济能力。因此，当1 台MMC 出线热稳裕度过低，而其他MMC 出线热稳裕度较高时，可以通过调节有功功率在MMC 之间的分配情况以提高直流系统整体的换流站出线热稳裕度λ。考虑了并联MMC 功率互济能力后，在计算MMC 出线热稳裕度时需要对式（21）进行修正。具体方法是通过改变有功功率在并联MMC 之间的分配情况，尽可能增大所有MMC中的最小出线热稳裕度。需要说明的是，当所有MMC 的出线热稳裕度相等时，所有MMC 中最小出线热稳裕度达到最大值。因此，考虑MMC 功率互济后，各台MMC出线热稳裕度可以由式（22）得到。

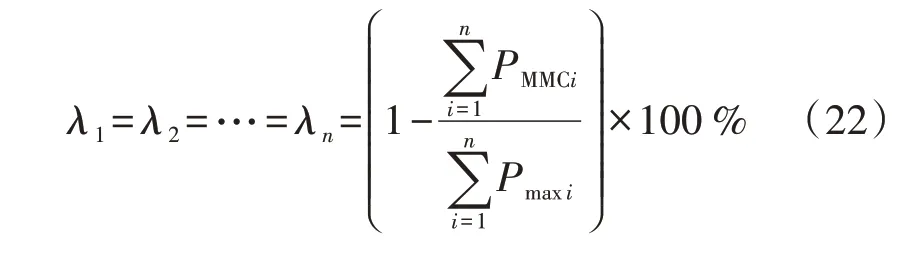
3 算例分析

本文采用3套江苏电网2023年规划数据进行算例分析，包括冬季高峰、夏季高峰以及汛期高峰。仿真软件为PSS／E。白鹤滩—江苏特高压混合级联直流系统为馈入江苏电网的双极直流，其馈入节点及附近部分网架结构如附录A 图A4 所示。逆变侧LCC通过2回线接入斗山、通过3回线接入常熟南，单回线路容量为3 500 MV·A。MMC1的2 条出线分别接入张家港与常熟北，线路容量均为2 718 MV·A。MMC2、MMC3分别通过2 回线接入木渎和玉山，单回线路容量为3 182 MV·A。稳态时直流功率一半由LCC送出，另一半由3台MMC送出，冬季运行方式下单极直流功率为2 000 MW，夏季与汛期运行方式下为4 000 MW。测试用系统参数见附录A 表A1。熟北站MMC1采用定直流电压控制，木渎站MMC2和玉山站MMC3采用定有功功率控制，3台MMC 的q轴外环均采用定无功功率控制（无功功率参考值为0）。

3.1 白鹤滩—江苏特高压混合级联直流系统模型验证

为验证白鹤滩—江苏特高压混合级联直流系统模型的正确性，在PSS／E 和BPA 中采用相同的江苏电网2023 年汛高数据进行仿真。选取故障为玉山—车坊双回线N-2 故障，具体故障逻辑为0.2 s 玉山—车坊双回线发生三相金属性接地短路故障，短路故障持续0.1 s 后跳开双回线，故障被切除。对比PSS／E 和BPA 这2 种软件下的仿真结果，白鹤滩—江苏特高压混合级联直流系统逆变侧MMC、LCC 的响应特性分别如附录A图A5、A6所示。

从图A5、A6 可以看出，本文所采用的白鹤滩—江苏特高压混合级联直流系统模型与BPA 软件中所用模型的响应特性基本吻合。鉴于BPA 已经被用于白鹤滩—江苏特高压混合级联直流工程的规划与安全稳定校核当中，其正确性得到国内电力行业的广泛认可。因此，本文所采用的模型可以正确反映白鹤滩—江苏混合级联直流系统的运行特性。

3.2 白鹤滩—江苏特高压混合级联直流系统稳态响应特性分析

当逆变侧换流母线电压保持不变、整流侧换流母线电压逐步降低时，整流侧出口直流电压udcr与电流idc有下降的趋势。为维持idc在整定值，整流站LCC 的触发角α不断减小直至其最小限定值αmin，在此期间逆变侧LCC的控制方式为定关断角控制。触发角α达到最小限定值后，整流侧LCC 失去对直流电流的控制能力，逆变侧LCC 控制方式从定关断角控制切换为定电流控制，而idc的整定值由VDCOL 确定。由于逆变侧MMC 换流母线电压无法降低，当逆变侧LCC 换流母线电压已经降为0 时，如果整流侧交流母线电压继续降低，则直流系统将失去电流控制能力。当整流站换流母线电压跌落至与逆变侧MMC 换流母线电压相同时，直流系统将发生断流。整流侧交流故障下混合级联直流系统响应特性如附录A 表A2 所示。由表可知，对于混合级联直流系统，如果整流侧交流电压跌落幅度较大，则直流系统将发生断流。在本次测试中，整流侧交流母线电压幅值低于0.46 p.u.时，混合级联直流系统发生断流。这一点与常规直流差别较大，常规直流通常在整流站换流母线电压跌落至0时才会发生断流。

接着，保持整流侧换流母线电压在正常值不变，逐步降低逆变侧LCC 换流母线电压。由于逆变侧LCC 和3 台MMC 接入同一交流电网，当LCC 换流母线电压跌落时，3 台MMC 的换流母线电压也会在不同程度上跌落。当逆变侧LCC 换流母线电压跌落时，混合级联直流系统响应特性如附录A表A3所示。

当逆变侧LCC 换流母线电压不断跌落时，逆变侧LCC 一直保持定关断角控制方式不变，整流侧LCC 的控制方式会发生变化。逆变侧LCC 换流母线电压跌落，VDCOL 投入，降低整流侧LCC 的电流指令值。在逆变侧LCC换流母线电压不断跌落的过程中，MMC 换流母线电压也会有所降低。由于LCC 和MMC 之间有一定电气距离，MMC 换流母线电压跌幅较小，MMC依旧可以正常输送功率。

然后，保持整流侧LCC换流母线电压不变，逐步降低逆变侧熟北站MMC1换流母线电压，得到混合级联直流系统响应特性，见附录A 表A4。由表可知，当熟北站MMC1换流母线电压严重跌落时，整流侧LCC 的电流指令值将由MMC 的最小直流电流限制决定。这是因为MMC1交流侧存在一个最大电流限制，MMC1出口处交流电压严重跌落时，MMC1交流侧的可送出功率受限。为保证MMC1换流母线电压不变，就需要整流侧LCC降低直流电流指令值。

最后，当木渎站MMC2换流母线电压跌落时，混合级联直流系统的响应特性如附录A 表A5 所示。由于熟北站MMC1采用定直流电压控制，当木渎站MMC2换流母线电压跌落时，MMC2功率无法正常送出，MMC1会分担一部分功率以保证直流电压不变。因此，相较于熟北站MMC1，当木渎站MMC2换流母线电压跌落时，白鹤滩—江苏混合级联直流系统基本不需要降低直流电流运行。另外，当玉山站MMC3换流母线电压跌落时，白鹤滩—江苏混合级联直流系统响应特性和木渎站MMC2换流母线电压跌落时基本相同，这里不再赘述。

3.3 逆变侧LCC换流母线电压稳定性评估

在冬季高峰、夏季高峰以及汛期高峰3 种运行方式下，在逆变侧LCC 的换流母线处施加一个无功扰动，根据式（9）计算逆变侧LCC换流母线的电压稳定系数λVSF，结果见附录A表A6所示。由表可知，在3 种运行方式下，λVSF均为正值，因此逆变侧LCC 的换流母线具有静态电压稳定性。

为评估逆变侧LCC 换流母线的暂态电压稳定性，在换流母线处设置持续时间为0.1 s 的三相金属性接地短路故障，通过仿真计算获得故障切除瞬间换流母线的电压数值Up，结果见附录A 表A6。由表可知，在不同运行方式下，故障切除瞬间逆变侧LCC换流母线电压跃升至约0.85 p.u.。因此，故障切除后逆变侧LCC换流母线电压并不能马上恢复到正常范围，表明系统的暂态电压稳定性略差，甚至引起逆变侧LCC长时间无法从换相失败中恢复。

3.4 MMC暂时过电压评估

利用仿真计算验证本文所提MMC 暂时过电压估算方法的准确性。设0.2 s 时，在采用定直流电压MMC 的换流母线处施加持续时间为0.1 s 的三相金属性接地短路故障。白鹤滩—江苏特高压混合级联直流工程中有3台MMC，考虑任一MMC都可以采用定直流电压控制，这里在不同运行方式下依次选择不同MMC 作为定直流电压MMC 进行仿真计算。MMC直流电压响应曲线如图2所示。

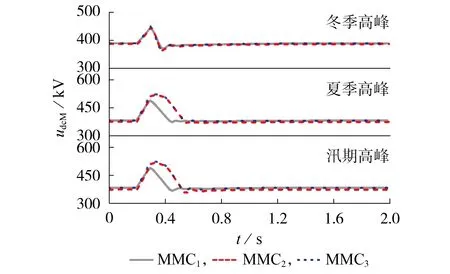
图2 不同运行方式下MMC直流电压响应曲线Fig.2 DC voltage response curves of MMCs under different operation conditions

然后利用提出的MMC 暂时过电压估算方法对不同工况数据进行估算，估算结果与仿真结果的对比如附录A 表A7 所示。表中，误差通过式（23）计算得到。这里，MMC直流电压的额定值为400 kV。

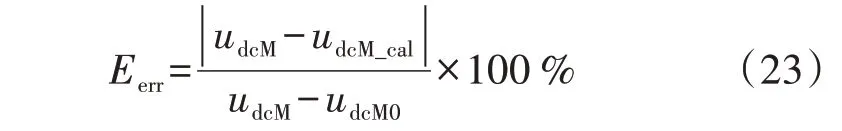
式中：Eerr为计算误差；udcM0和udcM_cal分别为MMC 直流电压估算值和稳态值。

通过对比结果可以看到，估算结果可以有效反映MMC 暂时过电压峰值水平。值得注意的是，该过电压估算方法并不是为了替代仿真计算，而是对现有规划方案进行评估，无法作为对MMC 进行绝缘配合的依据。利用该估算方法可以分析各类参数对MMC 过电压水平的影响，目的是为技术人员提供规划方案改善方向，故该估算方法的精度可满足需求。

实际上，影响交流故障下MMC 过电压水平的重要因素是MMC 换流母线之间的电气距离。MMC 换流母线之间的电气距离越近，单一短路故障造成的MMC 功率阻塞现象就越严重，MMC 过电压水平越高。下面，以ξMIIF作为母线之间电气距离的度量值，利用所提MMC 暂时过电压估算方法分析MMC 落点之间电气距离对过电压峰值的影响。

基于白鹤滩—江苏混合级联特高压直流工程实际数据，改变定直流电压MMC1与定有功功率MMC2之间的ξMIIF12，得到MMC暂时过电压峰值估算值udcMmax的变化曲线，如图3 上图所示。图中，考虑了直流系统满载和50%负载2 种负载情况，并且考虑了定直流电压MMC1换流母线短路故障是否引起逆变侧LCC 换相失败2 种情况。从图中可以看到，当2 台MMC 换流母线之间的ξMIIF12小于某一数值时，MMC暂时过电压峰值将不再发生变化。这是因为在这一区间，定有功功率MMC 换流母线电压跌落较小，该MMC 完全有能力按照指令值输出有功功率。MMC暂时过电压峰值随ξMIIF12变化率的波形如图3下图所示。可以看到，当dudcMmax/dξMIIF12不为0 时，其值随着ξMIIF12的增大而减小。MMC 暂时过电压峰值随ξMIIF13的变化情况与ξMIIF12类似，这里不再赘述。

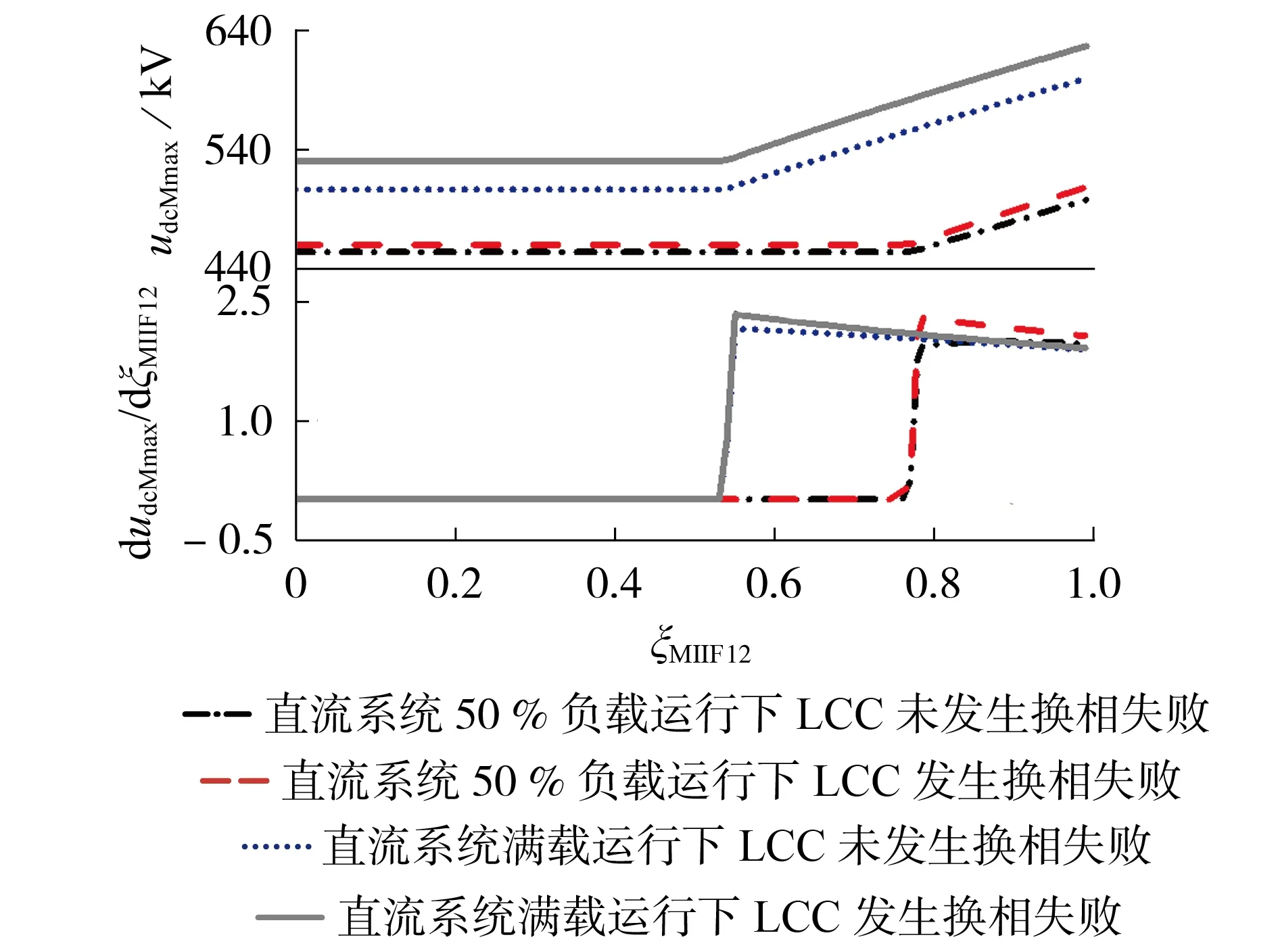
图3 MMC暂时过电压峰值与其随ξMIIF12变化率波形Fig.3 Waveforms of temporary overvoltage peak values and changing rates of peak values vs. ξMIIF12

基于江苏电网2023 年规划数据进行计算，白鹤滩—江苏特高压混合级联直流工程的3台MMC之间的ξMIIF位于dudcMmax/dξMIIF=0 的区间。任一MMC 采用定直流电压控制时，该MMC 换流母线发生三相金属性接地短路故障，另外2 台MMC 都可以按照指令值输出有功功率。因此，江苏电网规划的网架结构已经将MMC 暂时过电压峰值最小化，改变MMC 换流母线之间的电气距离已经不能再降低过电压水平。

3.5 逆变站出线热稳裕度计算

首先考虑逆变侧LCC出线热稳裕度。在正常运行方式以及逆变侧LCC 出线N-1／N-2 检修方式下进行计算，得到各种运行方式下逆变侧LCC 出线热稳裕度，如附录A 表A8 所示。由表可知，在汛期高峰LCC-斗山N-1 检修运行方式下，LCC 出线的热稳裕度过低，仅为4.30%。实际上，即使在N-1 检修方式下，LCC 依然有4 回出线，LCC 出线的总体输送能力是足够的，但是存在潮流分布不均的问题，可通过增设线路潮流调控设备缓解该问题。

然后分别在正常运行工况和出线N-1 检修工况下计算3 台MMC 的出线热稳裕度，得到结果如附录A 表A9 所示。由表可知，在正常工况和N-1 检修工况下，3台MMC均具有较高的热稳裕度，受端电网可以很好地消纳直流功率。但需要注意的是，每台MMC 只有2 条出线，当1 条MMC 出线运行于N-2检修工况时，该MMC 的功率必须由其他MMC 分担。在考虑了3 台MMC 的功率互济能力后，可以得到N-2 检修工况下MMC 出线热稳裕度，如附录A 表A10 所示。结果显示，通过MMC 之间的功率互济能力，即使在发生N-2 故障时，1 台MMC 无法输出功率，剩余MMC 也不属于重载状态，系统依然可以安全稳定运行。

4 结论

本文提出了一种混合级联直流系统运行特性分析方法，并针对白鹤滩—江苏特高压混合级联直流系统运行特性分析，得出以下结论。

1）通过不断降低白鹤滩—江苏特高压混合级联直流系统整流侧或逆变侧换流母线电压，得到直流系统稳态响应特性。结果表明，白鹤滩—江苏特高压混合级联直流系统在整流侧LCC换流母线电压低于0.46 p.u.时就会断流。对于逆变侧，当熟北站MMC 换流母线电压严重跌落时，受限于MMC 交流侧最大可输送功率限制，直流电流也会被限制在较低水平。木渎站或玉山站MMC 换流母线电压跌落基本不影响直流系统的功率传输能力。

2）白鹤滩—江苏特高压混合级联直流系统逆变侧LCC 换流母线静态电压稳定裕度充足，但是暂态电压稳定性略差，体现为交流短路故障切除后LCC换流母线电压不能马上恢复到正常范围。

3）白鹤滩—江苏特高压混合级联直流系统在受端电网交流短路故障下MMC 存在暂时过电压问题，且3 台MMC 换流母线之间的电气距离足够大，改变MMC 换流母线之间的电气距离已经不能再降低过电压水平。

4）白鹤滩—江苏特高压混合级联直流系统逆变侧出线容量充裕，在任意出线发生N-1故障时，不需要采取措施；在任意出线发生N-2故障时，通过改变MMC之间的功率分配即可避免过载问题。

附录见本刊网络版（http：//www.epae.cn）。