基于谐波状态空间理论的LCL型并网逆变器谐波交互及稳定性分析

林顺富，戴烨敏，颜昕昱，李东东，符 杨

（1. 上海电力大学 电气工程学院，上海 200090；2. 国网上海市电力公司市北供电公司，上海 200070）

0 引言

近年来，新能源分布式发电技术的研究成为当前的热点，并网逆变器是分布式发电的重要接口。随着逆变器装置的广泛应用，电网的电力电子化面临一定的挑战［1-2］。实际中恶劣、复杂的运行环境以及逆变器与电网的谐波交互过程造成并网电流的质量下降，影响分布式发电系统的稳定性［2-3］。因此，有必要对逆变器与电网的谐波交互作进一步研究。相比于传统的L 型滤波器，LCL 型滤波器可以对开关频次的电流谐波进行大幅削减，并且具有重量轻、体积小、成本低等优点，但高阶系统会导致谐振的发生［4］。文献［5］解释了出现谐振的根本原因，发现在滤波电容上串联电阻可以有效抑制谐振峰。文献［6-7］在无源阻尼的基础上提出了有源阻尼和改进有源阻尼的控制方式，在抑制谐振峰的同时降低了系统的功率损耗。

对变换器进行数学建模的方法可分为2 类：一类是基于平均算子的平均模型；另一类是基于多频率模型。前者是传统建模方法，包括电路平均法和状态空间平均法，大多用于单输入单输出系统的研究，具有建模便捷等优势［8-10］。但该模型精度仅在低频准确，不能获得系统所有的不稳定模式。常见的基于多频率模型的建模方法有多谐波小信号法［11］、描述函数法以及谐波状态空间HSS（Harmonic State Space）法。用于多输入多输出或频率耦合系统的建模，进一步反映频率耦合现象，具有较精确的优点。文献［12］推导出多种频率耦合产生原因的并网逆变器频率耦合模型，但建模中未给出具体的耦合系数，只分析了其对系统稳定性的影响。而利用HSS理论建立的数学模型可获得系统所有不稳定的模式。

有学者采用HSS法建立了包含频率耦合现象的变流器模型。文献［13］利用该方法建立了单相整流器的新数学模型，分析了电压外环的比例系数Kp以及频率耦合对其稳定性的影响。文献［14］建立了比例谐振控制下的三相整流器的数学模型，但未分析弱电网情况下谐波谐振等问题。文献［15］在上述文献的基础上建立了PQ 控制下的三相L 型并网逆变器的数学模型，进一步研究了频率耦合导纳矩阵，并分析了直流侧扰动对于交流侧的影响。

传统的阻抗建模通过等效框图推导输出阻抗表达式，利用阻抗判据判断弱电网下逆变器稳定，普适性强［16-17］。也有学者采用dq阻抗建模［18-19］、正负序阻抗建模［20］和谐波线性化建模方法［21］建立逆变器输出阻抗，通过电网阻抗和LCL 型并网逆变器的输出导纳绘制奈奎斯特曲线来判断系统稳定性，但不能较好地反映逆变器的谐波特性。

在逆变器的HSS模型中输出阻抗的精度与所考虑的谐波阶数相关，模型中考虑的谐波阶数越高，输出阻抗模型的精度越高，可按照不同频率对逆变器的输出阻抗进行建模，从而获得更精确的逆变器输出阻抗模型。

本文利用HSS理论建立了基于比例积分PI（Proportional Integral）控制和电容电流反馈有源阻尼控制下的三相LCL型并网逆变器的数学模型。在该模型下分析并网逆变器与电网之间的谐波交互影响：①公共连接点PCC（Point of Common Coupling）处的背景谐波电压对直流侧电压和并网电流的影响；②逆变器直流侧扰动电压对并网电流的影响。进一步推导HSS理论下谐波传递函数矩阵并量化了它们之间的耦合系数。此外提出了一种基于HSS的阻抗分析方法，用以揭示弱电网下系统发生谐波振荡的机理。通过将实验、仿真模型结果与数学模型结果进行对比，验证了本文理论分析的有效性和分析结果的正确性。

1 HSS理论

利用状态空间平均法建立的系统数学模型为线性时不变LTI（Linear Time Invariant）系统，具体如下：

式中：A、B、C、D为常数；x(t)为状态变量；y(t)为输出变量；u(t)为输入变量；t为时间常数。该方法建模简单，但精确度较低。

为获得精确的数学模型，利用HSS 理论建立线性时变LTV（Linear Time Varying）系统，根据电路的周期性对其进行线性化。该方法可将式（1）转换为：

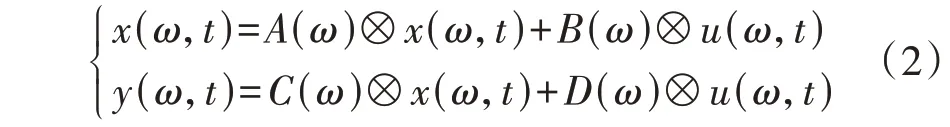
式中：⊗为卷积符号；A(ω)、B(ω)、C(ω)、D(ω)为时不变参数；x(ω，t)、u(ω，t)和y(ω，t)分别为与ω相关的时变状态变量、时变输入变量和时变输出变量。

根据欧拉公式可将连续的周期函数分解为傅里叶级数的指数形式。电路参量具有动态特性，需要加入暂态量est。以电流ig为例，可得：

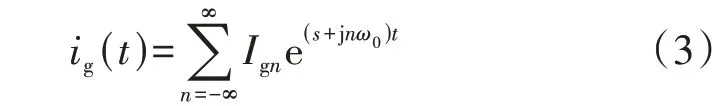
式中：ω0为基波角频率；Ign为n次谐波傅里叶系数。

根据谐波平衡的原理对式（2）等号两边进行约分可得：

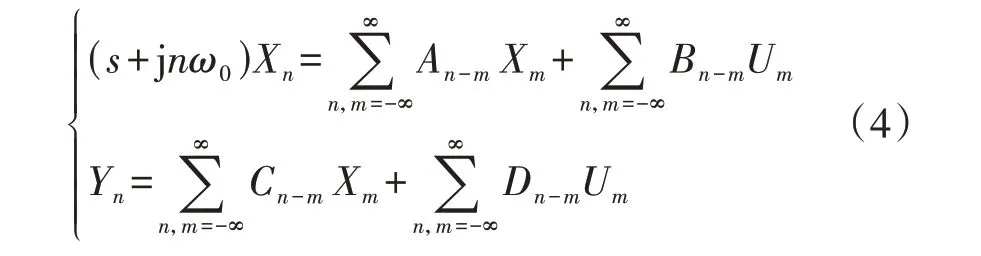
式中：An-m为状态系数；Bn-m为输入系数；Cn-m为输出系数；Dn-m为关联系数；Xn、Xm为状态量；Um为输入量；Yn为输出量。

通过式（5）将频域输出变量Y转化为时域输出变量y(t)。

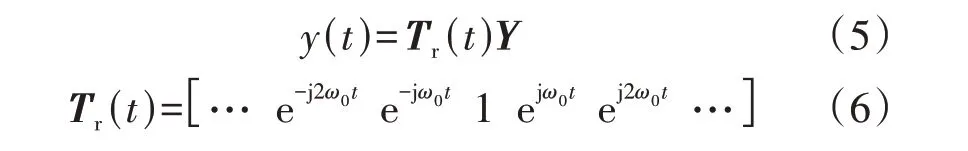
2 三相LCL型并网逆变器数学建模

2.1 并网逆变器系统结构和控制结构

电压源型三相LCL型并网逆变器系统结构图如图1 所示，基于有源阻尼反馈和电流环控制的结构图如图2 所示。图1 中：Cdc为稳压电容；L1、L2为滤波电感；C0为滤波电容；R1、R2为寄生电阻；vdc、idc分别为稳 压 电 容 电 压 和 电 流；vinva，b，c为 逆 变 器 输 出 电 压；iLa，b，c为电感电流；iCa，b，c为滤波电容的电流；iga，b，c为并网电流；vpcca，b，c为PCC处电压；Edc为直流电压；Rdc为电阻；swa，b，c为开关函数；vCa，b，c为电容电压。图2中：Igdref、Igqref分别为d、q轴参考电流；iCd、iCq和igd、igq分别为由abc坐标系转换到dq坐标系获得的d、q轴滤波电容电流和并网电流；K为电容电流的有源阻尼反馈系数。

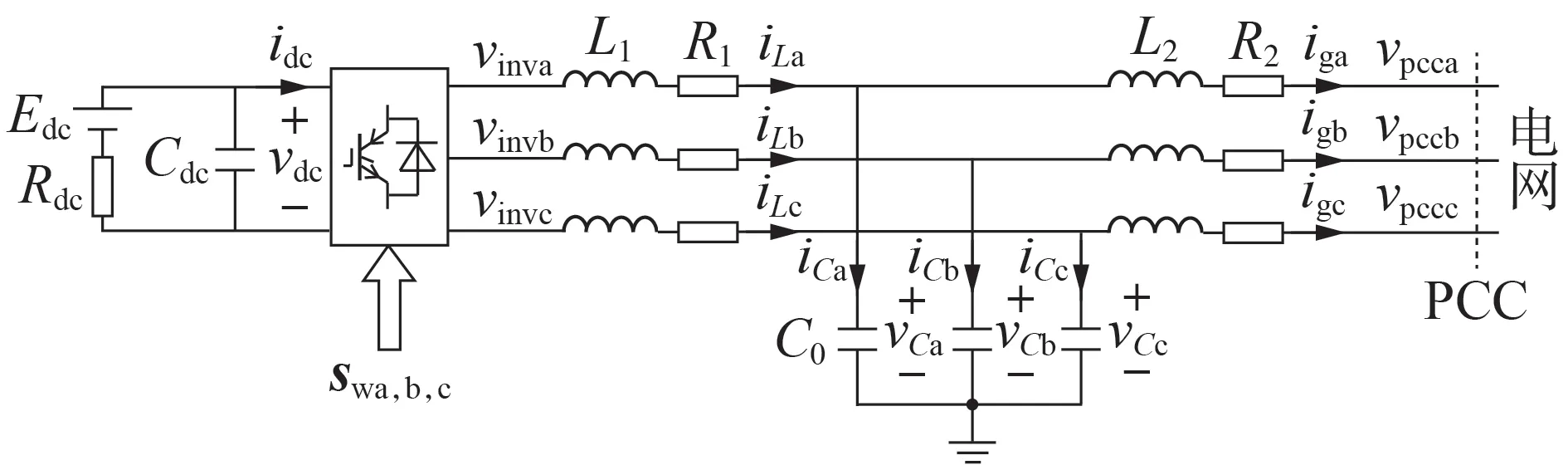
图1 三相LCL型并网逆变器系统结构图Fig.1 Structure diagram of three-phase LCL grid-connected inverter

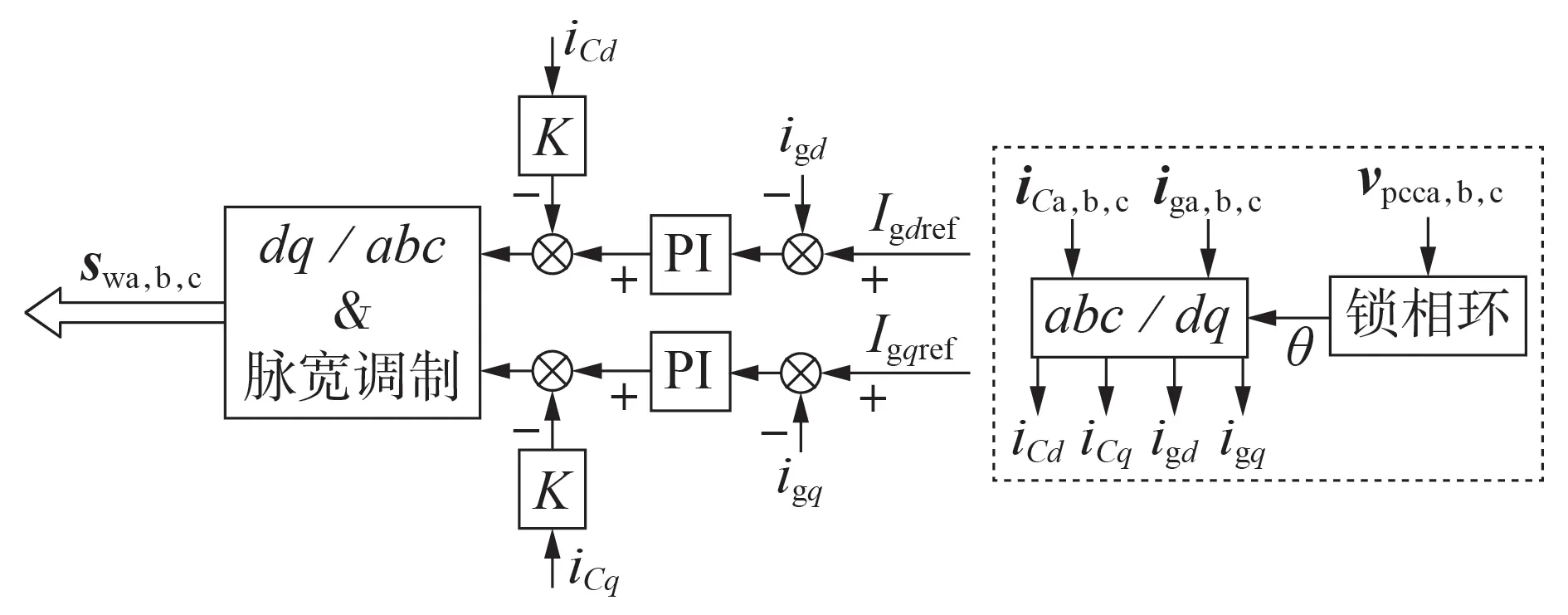
图2 三相LCL型并网逆变器控制框图Fig.2 Control block diagram of three-phase LCL grid-connected inverter

2.2 并网逆变器电路结构数学建模

根据图1 所示的三相LCL 型并网逆变器系统结构，在稳态工作点处对模型进行谐波线性化处理，可得线性化的时域电路方程，如式（7）—（10）所示。

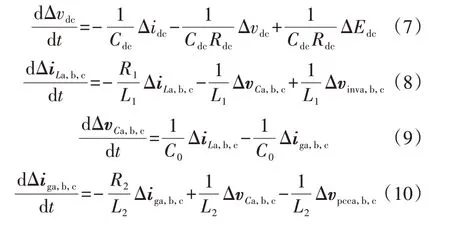
式中：Δ 表示扰动变量。将式（7）—（12）关系式转换成形如式（1）的状态方程，再经式（4）转换成频域的HSS模型，可得：

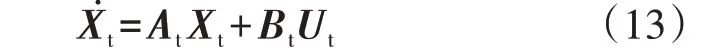
式中：Xt=［ΔIga，ΔIgb，ΔIgc，ΔVCa，ΔVCb，ΔVCc，ΔILa，ΔILb，ΔILc，ΔVdc］T，其中ΔIga由Δiga经过指数形式傅里叶分解后的傅里叶系数组成，其维数大小由所要研究的谐波次数决定，若研究k次谐波间的交互关系，则ΔIga为2k+1 阶列向量，其余元素类似；Ut=［ΔVpcca，ΔVpccb，ΔVpccc，ΔSwa，ΔSwb，ΔSwc，ΔEdc］T，其元素含义与Xt相似；矩阵At、Bt的表达式分别见附录A 式（A1）、（A2），其中O为零矩阵，T［·］为托普利茨矩阵，I为单位矩阵，N为运算中产生的对角矩阵。

2.3 并网逆变器控制结构数学建模

控制结构中采用了PI 控制的电流内环，并考虑了电容电流有源阻尼反馈。当锁相环带宽较小时，电压扰动对锁相环输出角度的影响较小［12］，可忽略锁相环带来的影响，并假设锁相环获得的角度为θ。HSS模型下PI控制函数GPI表示为：

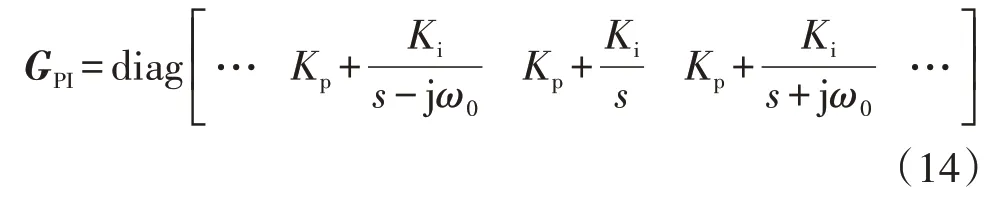
式中：Kp为比例系数；Ki为积分系数。

为适应HSS模型，Park变换矩阵GPark为：

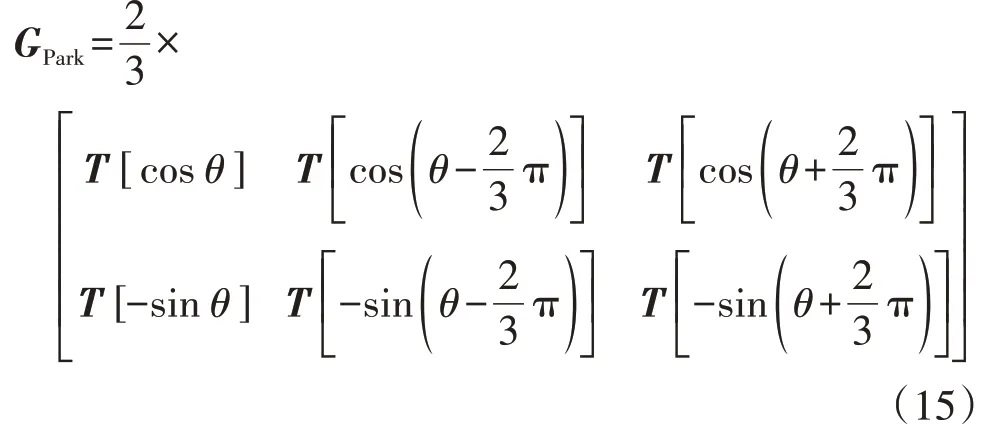
根据图2的控制结构可列写如下HSS方程：

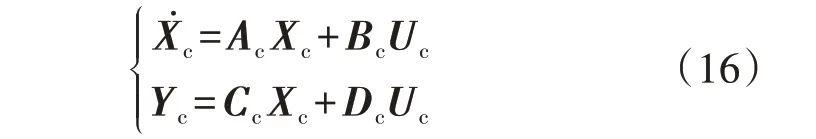
式中：Xc=［XPId，XPIq］T，XPId、XPIq分别为d、q轴的状态变量；Yc=［ΔSwa，ΔSwb，ΔSwc］T；Uc=［ΔIgd，ΔIga，ΔIgb，ΔIgc，ΔILa，ΔILb，ΔILc］T；矩阵Ac、Bc、Cc、Dc的表达式分别见附录A式（A3）—（A6）。

2.4 谐波传递函数

为研究背景谐波电压、直流纹波对系统造成的影响，以及直流纹波对网侧的影响，需要将HSS方程化简为谐波传递函数。

HSS方程为：

通过等式变换可得：

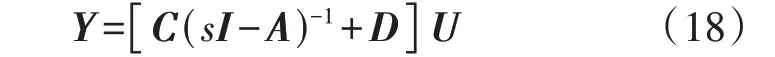
令：

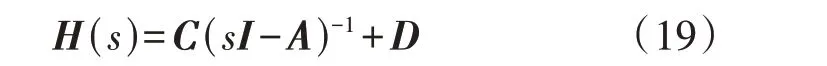
式中：H(s)为谐波传递函数矩阵。相较于线性时不变模型，HSS 模型可用于研究不同频次谐波间的传递关系。可将H(s)定义为：

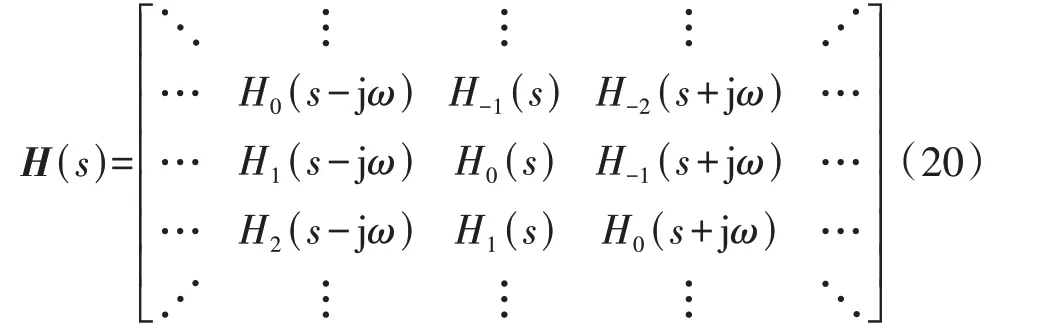
式中：矩阵元素为耦合系数，且都为复数。当式（20）中s=0时，通过对矩阵进行截断，可获得稳态时输出变量与输入变量间的耦合系数阵。

2.5 HSS模型下耦合系数分析

2.5.1 背景谐波电压与并网电流

假设在交流侧产生了p次谐波电流igξ，p（ξ=a，b，c），并将其时域表达式变换为如下傅里叶级数的形式：

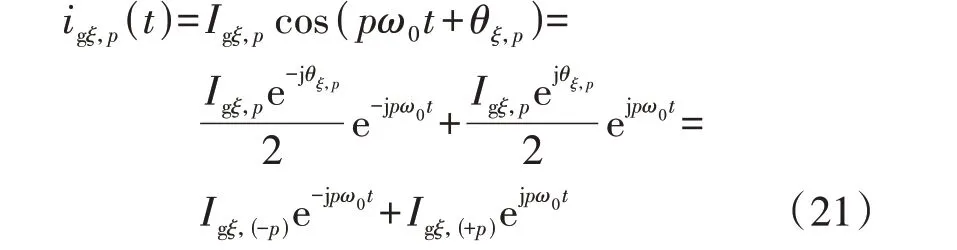
式中：Igξ，p为谐波电流幅值；θξ，p为谐波电流的相角；Igξ，(-p)、Igξ，(+p)分别为p次谐波电流的傅里叶负系数和傅里叶正系数。根据HSS方程推导可知：

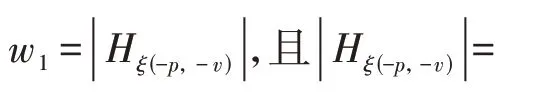
2.5.2 背景谐波电压与直流侧电压

假设在直流侧产生了r次直流扰动电压vdc，r，并将其时域表达式变换为如下傅里叶级数的形式：

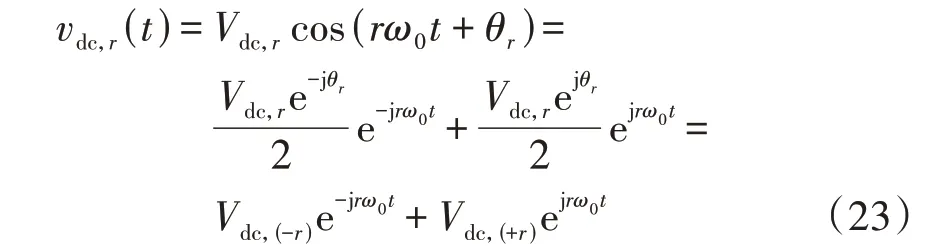
式中：Vdc，r为直流扰动电压幅值；θr为直流扰动电压的相角。根据HSS方程推导可知：

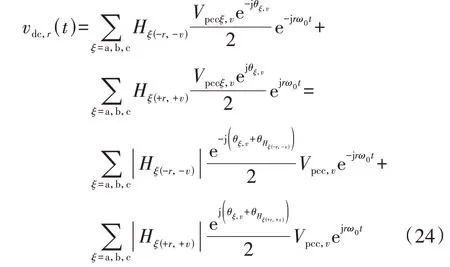
式中：Vpcca，v=Vpccb，v=Vpccc，v；Hξ(±r，±v)表示傅里叶系数为±r次的直流扰动电压与傅里叶系数为±v次的背景谐波电压之间的耦合关系。对比式（23）与式（24）可知，耦合系数w2与Hξ(+r，+v)有关。

2.5.3 直流侧扰动电压与并网电流

根据HSS方程推导可知：

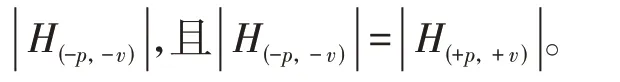
2.6 并网逆变器阻抗建模

传统阻抗特性分析可用于研究谐波谐振的产生。该方法需建立并网逆变器的输出阻抗模型。逆变器的诺顿等效电路如附录A 图A1 所示。通过电网阻抗Zg与输出阻抗Zinv（即1/Yinv）的幅频特性曲线交截频率处的幅值裕度与相角裕度来判断并网系统的稳定性。

逆变器完整的HSS数学模型可表示为：

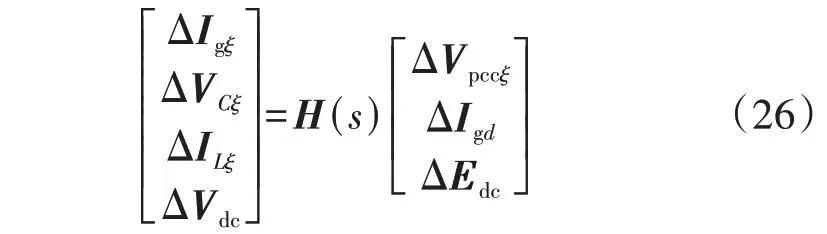
由式（26）可以得到式（27），并进一步获得输出导纳。

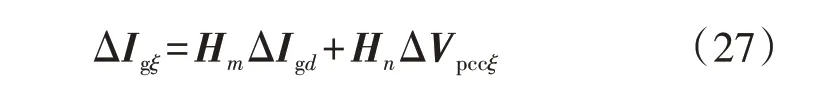
式中：ΔIgξ、ΔVpccξ分别为并网电流ig、PCC 处电压在HSS理论中的谐波系数矩阵；Hm、Hn为相应的谐波传递函数矩阵。获得的输出导纳矩阵示意图如附录A图A2 所示。对所获得的输出导纳矩阵进行求逆来获取输出阻抗矩阵。由于HSS模型是多输入多输出系统，相较于传统模型可获得传统模型不具备的特性，能分析更多的系统不稳定模式。

3 仿真实验

在Simulink 中搭建了逆变器的仿真模型，在MATLAB 中实现了HSS 数学模型，仿真模型参数如附录B 表B1 所示。将仿真结果与数学模型结果进行对比分析。

根据表B1 中的参数绘制式（21）、（22）中输出变量Ig与输入变量Vpcc之间的耦合系数w1示意图，如图3 所示。从图中可看出，输入变量单频次扰动会造成输出变量在该频次下的响应。式（24）、（25）中耦合系数的示意图分别如附录B图B1、B2所示。

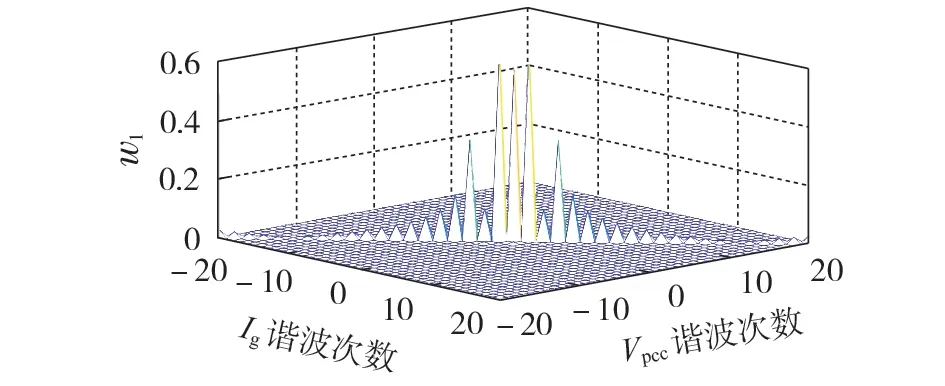
图3 输出变量Ig与输入变量Vpcc的耦合系数Fig.3 Coupling coefficient between output variable Ig and input variable Vpcc

3.1 背景谐波电压对并网电流与直流电压的影响

为了验证HSS 模型的有效性，设置多种背景谐波电压工况，如表1所示。

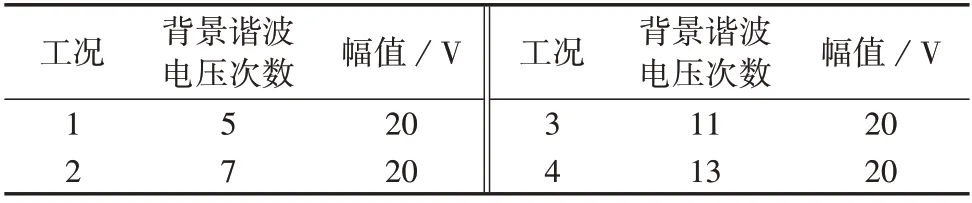
表1 背景谐波电压工况Table 1 Conditions of background harmonic voltage

在HSS 模型中，对20 次及以内的谐波进行分析，工况1下理论与仿真结果对比图如图4所示。由图可见，电网含有5 次谐波电压，会在PCC 处产生5次谐波电流，在直流侧产生6次谐波电压扰动。

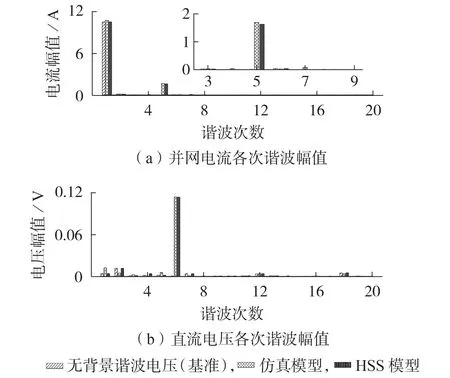
图4 工况1下理论与仿真结果对比Fig.4 Comparison of theoretical and simulative results under Case 1

工况2—4 下理论与仿真结果对比图分别如附录B 图B3—B5所示。表2、3对比了工况1—4下主要响应变量的仿真值与HSS 模型计算值，表中HSS模型计算值为耦合系数与输入变量幅值乘积。

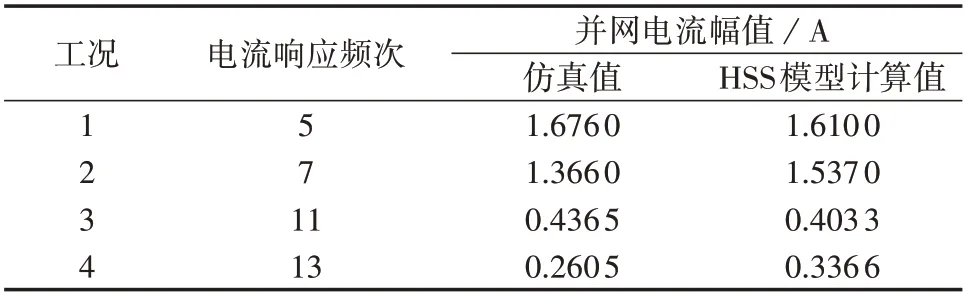
表2 PCC处含背景谐波电压时并网电流幅值对比Table 2 Amplitude comparison of grid-connected current at PCC with background harmonic voltage

由表2、表3、图3 以及附录B 图B1 可知：当PCC处含有6h±1 次谐波电压扰动时，除了会造成同一频次的并网谐波电流外，还会在直流侧产生6h次的谐波电压扰动。

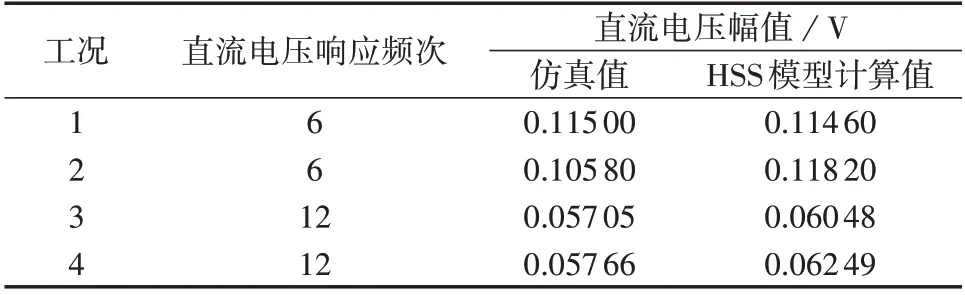
表3 PCC处含背景谐波电压时直流电压幅值对比Table 3 Amplitude comparison of DC voltage at PCC with background harmonic voltage

3.2 直流电压扰动对并网电流的影响

为研究逆变器直流侧与交流侧的谐波交互关系，在直流侧设置了2 种直流电压扰动工况：①工况5 为直流侧含300 Hz 的20 V 电压扰动；②工况6 为直流侧含600 Hz的20 V电压扰动。工况5、6下理论与仿真结果对比分别如附录B 图B6、B7 所示。表4给出了工况5、6 下主要响应变量的仿真值与HSS 模型计算值的对比。

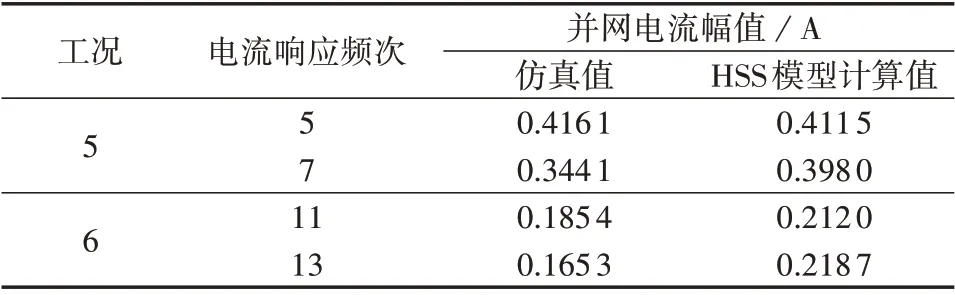
表4 直流侧含谐波电压扰动时并网电流幅值对比Table 4 Amplitude comparison of grid-connected current at DC side with harmonic voltage disturbance

3.3 弱电网下逆变器的稳定性研究

奈奎斯特图可反映弱电网下逆变器稳定性，但不能较好地反映逆变器的谐波特性。基于HSS的逆变器输出阻抗建模可较好地反映弱电网下逆变器的频率特性，能对系统的响应和动态性能的变化进行更细化的分析，具体如附录B 图B8 所示。图中阻抗曲线是由逆变器HSS模型中各个频次下的输出阻抗谐波传递函数绘制而成，如H-1是由Vpccξ，-1与Igξ，-1所对应的输出阻抗。可以看出，不同频次下的输出阻抗具有不同的幅频特性。

由图B8 可以看出：当Lg=1.5 mH 时，电网阻抗Zg的幅频曲线与H-5的幅频曲线在236 Hz处先相交，然后再与H0的幅频曲线相交；当Lg=3 mH 时，Zg的幅频曲线与H-3的幅频曲线在134 Hz处先相交，并且随着电网阻抗的增大，输出阻抗与电网阻抗Zg的交截频率在不断地向左移动；当Lg=6 mH 时，Zg的幅频曲线与H0的幅频曲线在131 Hz 处相交，影响逆变器并网系统的控制性能，会导致系统不稳定。

分别对仿真中的电流数据进行了傅里叶分析，逆变器在Lg=1.5 mH 和Lg=3 mH 情形下运行相较于Lg=0 情形下的并网电流总谐波畸变率（THD）变化值如附录B 图B9 所示。可以看出，当电网阻抗的幅频曲线未与H0曲线相交于236 Hz 和134 Hz，但与其他对数频率特性曲线相交时，该交点频率与测得的逆变器输出电流中的谐波频率密切相关，导致并网电流电能质量变差。

4 实验验证

为进一步验证所提方法的有效性，搭建了基于RT-LAB 的实时仿真平台实验，使用示波器对I／O口输出进行观测。实验参数与仿真参数相同。实验平台如附录C图C1所示。

RT-LAB实验中获得的并网电流波形图如图5所示。数学模型中获得的并网电流波形图如图6所示，分别在0.5 s 和1 s 时对工况进行切换。对比图5 与图6可看出，HSS模型可以反映谐波传递特性，并且实验结果与理论结果一致，验证了HSS模型的有效性。

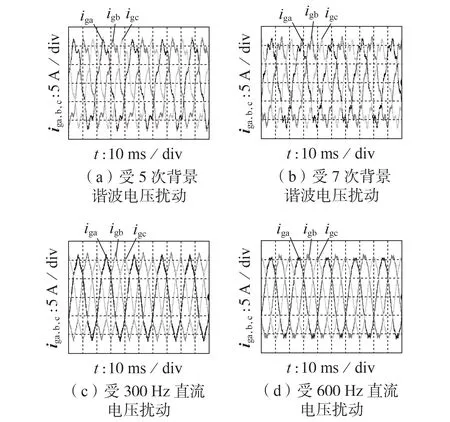
图5 不同工况下并网电流的实验波形Fig.5 Experimental waveforms of grid-connected current under different conditions

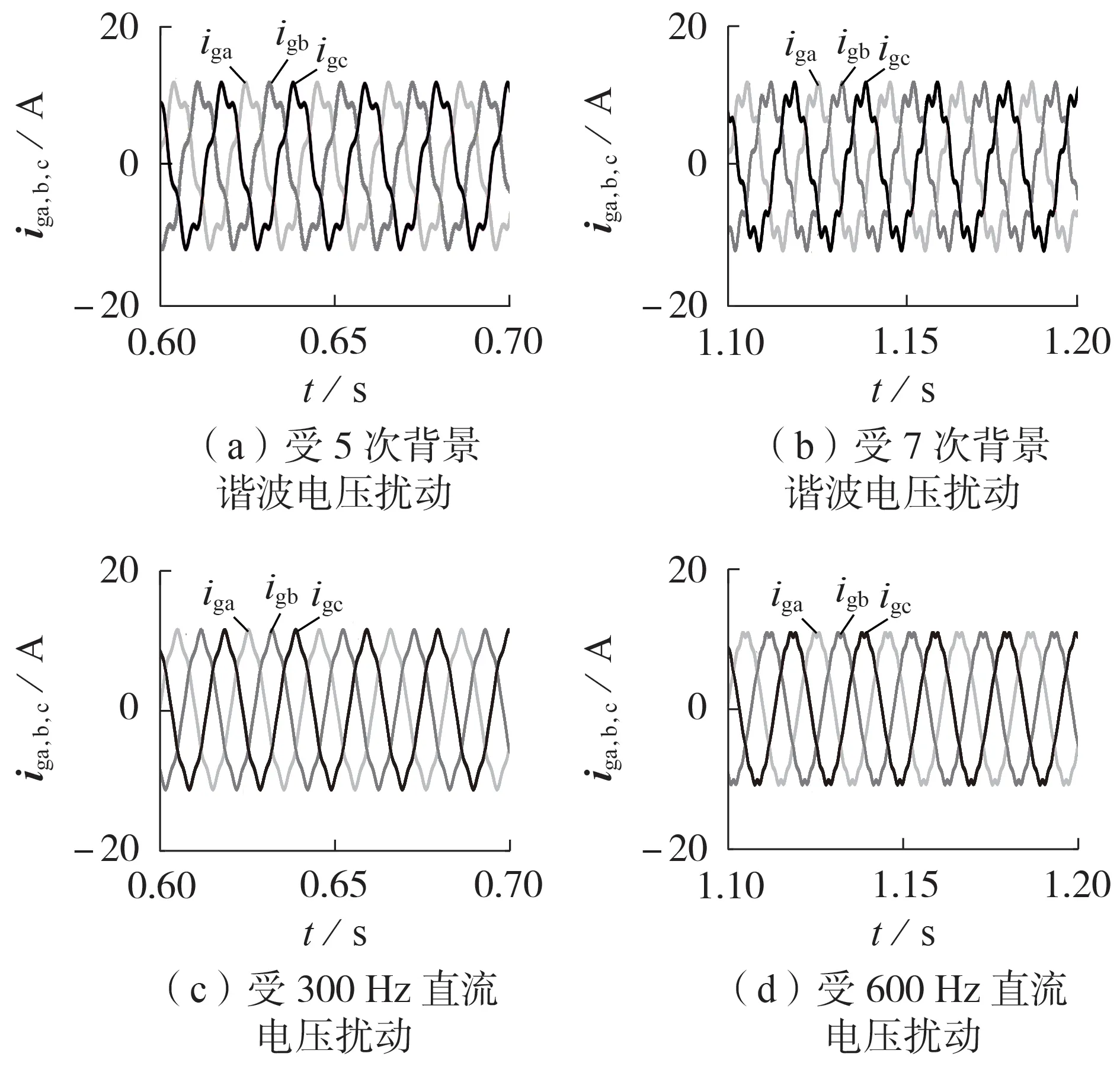
图6 不同工况下并网电流理论波形Fig.6 Theoretical waveforms of grid-connected current under different conditions

附录C 图C2 为不同工况下实验与理论的快速傅里叶变换（FFT）幅值对比图。从图中可看出，HSS模型结果与RT-LAB 实验结果具有较高的符合度。HSS 模型可较好地反映交流与直流系统之间的谐波传递特性。

通过实验对弱电网情形进行了验证，分别在0.5 s 时接入Lg=1.5 mH，在1 s 时接入Lg=3 mH，在1.5 s时接入Lg=6 mH，实验波形如图7所示。可以看出，当Lg=6 mH时逆变器并网系统出现不稳定。

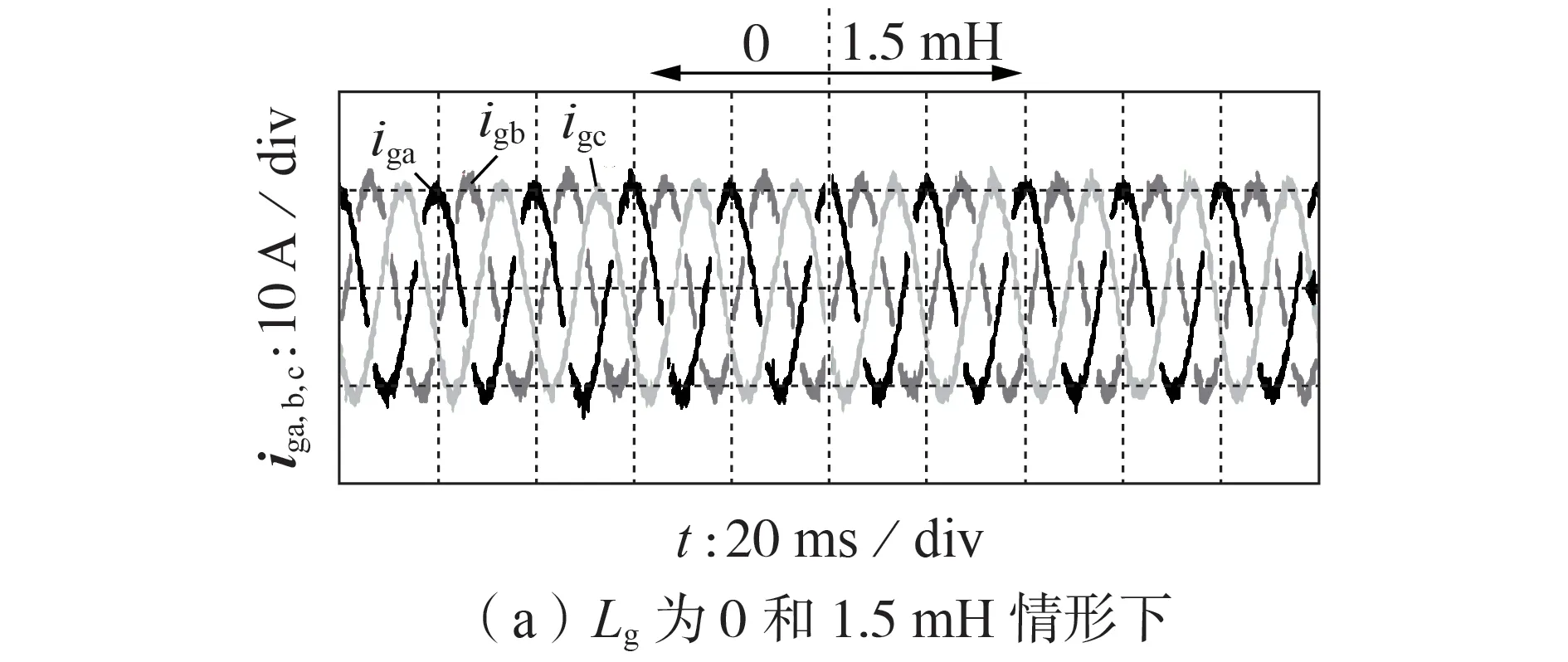
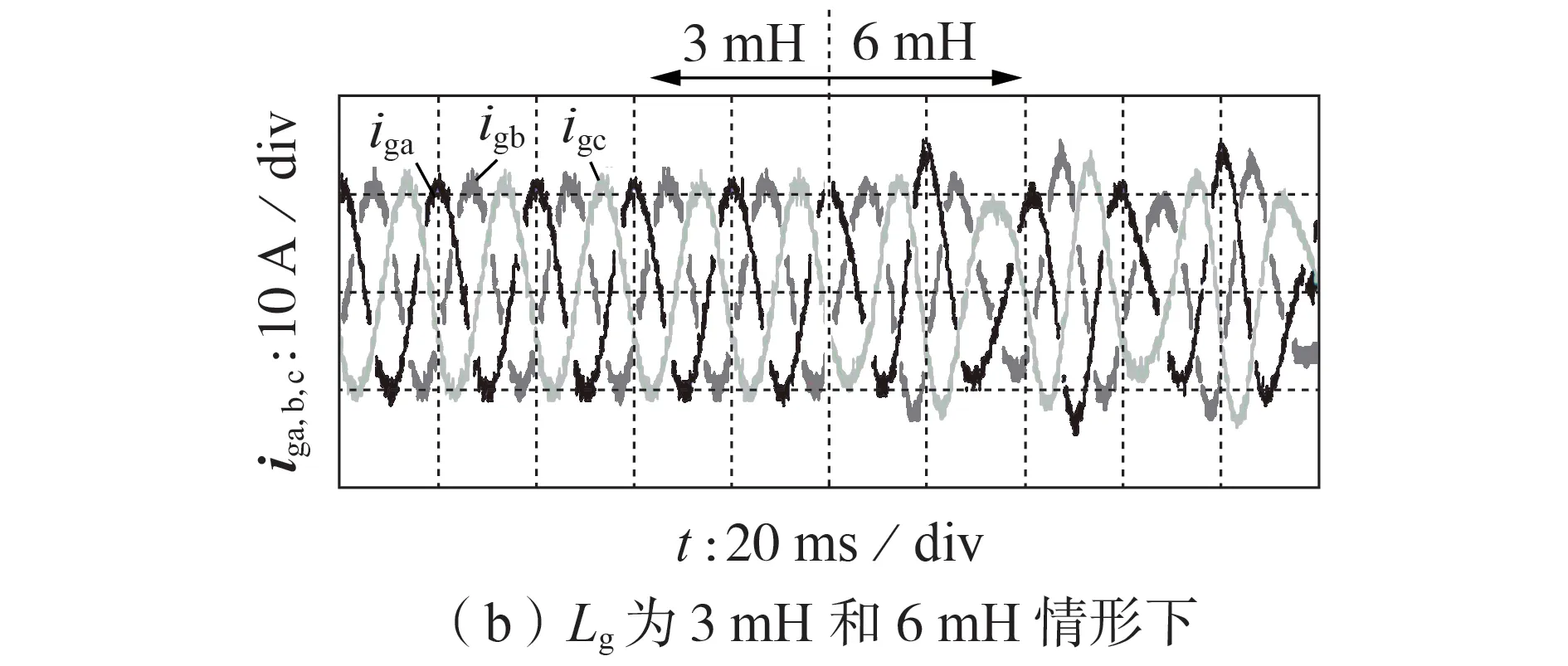
图7 不同电网阻抗下并网电流实验波形Fig.7 Experimental waveforms of grid-connected current under different grid impedances

5 结论

本文采用HSS 理论对PI 调节器和电容电流反馈有源阻尼控制下的三相LCL型并网逆变器进行建模，分析了电网与并网逆变器之间的谐波交互情况，得到如下结论。

1）对于逆变器内部的频率耦合特性，采用HSS法对逆变器进行建模，可以完整地分析谐波耦合过程。当PCC 处含有6h±1 次谐波电压扰动时，除了会造成同一频次的并网谐波电流外，还会在直流侧产生6h次的谐波电压扰动。直流侧含有6h次谐波电压扰动会在交流侧产生6h±1 次的谐波电流响应。利用谐波传递函数矩阵可推导交流侧与交流侧、交流侧与直流侧的耦合系数。利用HSS理论建立的模型可定量分析背景谐波电压对直流侧的影响、直流电压扰动对交流侧谐波电流的影响。

2）弱电网下，利用传统阻抗分析法对系统稳定性分析时不能获得所有的不稳定模式。基于HSS模型的阻抗分析法体现出与传统建模不同的特性，能具体分析不同频率下的逆变器输出阻抗与电网阻抗的谐振情况，可以较好地反映逆变器并网系统谐振特性及稳定性。

附录见本刊网络版（http：//www.epae.cn）。