基于主从博弈的配电网-多综合能源系统协调规划
2022-06-15刘文霞高雪倩刘宗歧邓诗语刘耕铭
刘 畅,刘文霞,高雪倩,刘宗歧,邓诗语,刘耕铭
(华北电力大学 新能源电力系统国家重点实验室,北京 102206)
0 引言
为促进新能源消纳,减少环境污染,提高能源利用效率,有关综合能源系统(IES)的研究日益广泛。IES 通过能源耦合设备实现对多种能源的耦合互济和梯级利用,以满足用户日益多样化的用能需求,同时多能源系统的互补替代性减小了单个能源系统发生故障对整个系统供能可靠性的影响[1],降低了对外部能源网络可靠性的依赖程度。随着IES接入电网的规模逐渐增大,用户对电网的电量与可靠性需求将逐渐减小,导致电网设备利用率大幅降低。如何对电网和IES 进行协调规划,充分利用IES多能耦合带来的可靠性价值,对延缓电网投资、降低整体供能成本具有重要意义。
目前关于配电网和IES 规划的研究主要集中在双方独立规划方面,对两者联合规划的研究较少。在IES 规划方面,文献[2]考虑联络线峰谷差和电网运行效益,以经济性最优为目标建立了IES 规划模型。文献[3]通过对经济性优化模型和可靠性校验模型进行循环迭代,得到协调可靠性与经济性的IES规划方案。文献[4]采用证据理论,建立了计及综合需求响应不确定性的IES 双层规划模型,并采用差分进化算法和求解器进行求解。文献[5]考虑负荷、可再生能源和购能价格的不确定性,构建了基于粒子群优化-区间线性规划的IES 双层优化模型。在配电网规划方面,文献[6]构建了配电网和分布式发电机组扩展规划模型。文献[7]提出了考虑风电不确定性的配电网扩展规划模型,并采用割平面法进行求解。文献[8]构建了考虑不确定性和可靠性的配电网和分布式发电的动态扩展规划模型。文献[9]构建了综合考虑分布式电源和电动汽车时空特性的配电网规划模型,并采用蒙特卡洛模拟嵌入双种群协同进化遗传算法对模型进行求解。在联合规划方面,文献[10]构建了考虑IES、分布式电源和电动汽车充电站的配网规划模型。文献[11]以总成本最小为目标建立了电转气设备、风电场与IES协同规划模型,并将其转化为混合整数线性规划问题进行求解。随着市场开放,IES 将由社会资本投资,与配电网作为独立的主体,利益诉求不同,且在供需关系下彼此相互影响。现有规划方法未考虑配电网和IES 之间的交互行为,以及电价对可靠性投资配置的引导,造成投资冗余、设备利用率低下、经济性差等问题,违背了发展综合能源的初衷。博弈理论能较好地刻画各主体的相互影响,平衡各方收益,其中主从博弈理论在能源供需互动方面已经得到了广泛应用[12]。
本文通过分析配电网投资运营商(DSO)和IES投资运营商在供需互动和共同保障用户可靠性关系下的利益矛盾,提出了利用考虑可靠性的电价为经济手段,调动两者开展协同优化规划思路;考虑可靠性与成本提升的关系,并借鉴国外可靠性奖惩机制,建立了考虑可靠性的分段电价模型;基于此,建立了DSO 与IES 投资运营商的主从博弈协调规划模型,上层领导者DSO 以利润最大为目标同时优化电价制定和扩展规划策略,下层跟随者各IES 投资运营商以成本最小为目标同时优化设备配置和运行策略;采用差分进化算法与OPTI 求解器求解模型,并基于算例仿真验证了本文模型在提高各主体经济效益、降低整体供能成本方面的有效性与合理性。
1 配电网-多IES博弈规划行为
1.1 博弈关系分析
在未来配电系统中大规模接入IES 的情况下,将由DSO 与IES 投资运营商共同承担对终端用户的电能及其他能源供给的责任,DSO 作为配电系统规划与运营的主体,在市场中承担配、售电的角色,从上级电网购电再将电能出售给用户,利用差价赚取收益。IES 投资运营商从配电网购电,从气网购气,通过内部能量生产、传输、转换设备满足用户的电/热/冷能源需求。双方在规划时不仅要保证终端用户的电量需求,还要提高供能充裕性使其有一定的可靠供电能力。DSO与IES之间的关系见图1。
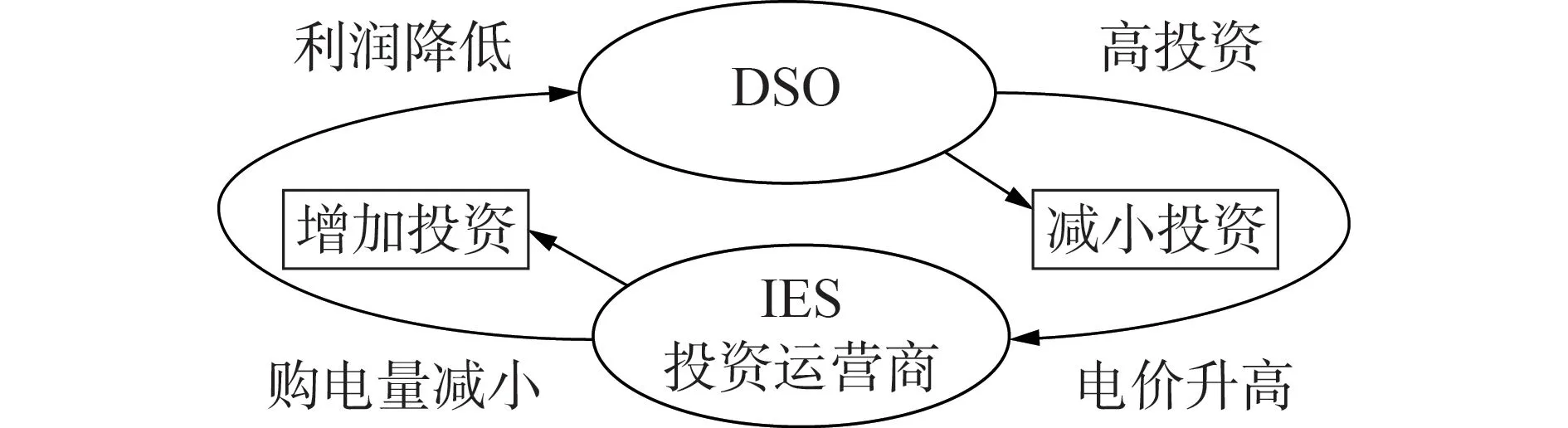
图1 DSO与IES之间的关系图Fig.1 Relationship diagram between DSO and IES
DSO 投资越大,可靠性越高,则接入的IES 只需较少投资就能满足用户的可靠性需求,DSO 的高投资导致电价较高,IES可能更愿意通过增加自身设备投资来提高多能耦合性,以保障对用户的供能可靠性,从而减少购电,造成DSO 售电收入减小,DSO 需要减小投资,否则会引起电价的进一步升高,再次导致购电量缩减,设备利用率降低,经济性更差。
充裕性和可靠性的提升必须追求最经济的原则,仅由一方承担会造成投资冗余,经济性难以保证。双方若能根据各自可靠性提升成本合理分担对用户的可靠性责任,这对降低整体供能成本、提高能源资源利用效率具有重要意义。
IES具有一定可靠性空间,降低了对配电网可靠性的依赖程度,同时希望买到更便宜的电。DSO 希望在满足用户用能需求的前提下,降低投资,提高利润和设备利用率。双方在规划时只有相互协调才能兼顾彼此利益,实现共赢。不仅DSO 制定的电价会影响IES 的需求,需求也会反作用于价格。双方具有彼此独立的利益诉求,均以实现自身利益最大为目标进行决策,且相互影响,自然存在博弈关系。
1.2 主从博弈过程
博弈理论是解决存在利益关联或冲突的多方主体如何制定决策的有效手段。主从博弈属于动态的非合作博弈,参与者地位不平等是主从博弈区别于经典博弈最根本的差别。在主从博弈中,各主体具有不同的地位与决策顺序,领导者具有领导优势,能够在博弈中占据先机或者有利位置,跟随者须跟在领导者之后做出决策。
本文协调规划场景主要涉及DSO 和IES 投资运营商这2类利益主体,DSO 作为多个IES唯一的供能方,在决策中更具主导权,2类主体地位不同。
决策时DSO 先结合市场信息以利润最大为目标,优先制定扩展规划方案及售电电价,各IES 被动接受DSO 制定的决策信息,结合用户负荷需求,灵活调整自身设备配置方案及运行策略,决策存在先后次序,构成了以DSO 为领导者、多个IES 投资运营商为跟随者的主从博弈关系。2类主体顺次决策,彼此影响,并且不断根据对方策略调整自身策略以实现利益最大,主从博弈不断循环迭代最终达到均衡。
2 配电网-多IES主从博弈协调规划模型
首先,由博弈的4 个要素建立主从博弈框架;然后,分别构建2 类主体的规划收益模型,并将其嵌入主从博弈框架,建立一主多从的协调规划模型。
2.1 主从博弈模型框架
博弈模型的4个要素如下。
1)参与者。主从博弈领导者为DSO,跟随者为n个IES投资运营商。
2)策略。DSO 的策略包括规划和定价策略,规划策略为线路的升级改造或新建、变电站的扩容或新建策略,将其分别记作ψl、ψs,定价策略为制定考虑可靠性的电价策略,记作ψρ,则DSO 的策略集合ψDSO={ψl,ψs,ψρ};IES 投资运营商的策略包括规划和运行策略,分别为各设备类型容量的配置策略、各机组出力以及购能策略,将IES 投资运营商m的规划、运行策略分别记作γinv,m、γope,m,则策略集合γIES,m={γinv,m,γope,m}。所有策略只能在其策略空间内取值,将DSO 与IES 投资运营商m的策略空间分别记作QDSO、QIES,m,则ψDSO∈QDSO,γIES,m∈QIES,m。
3)效用函数。DSO 以配电网扩展规划后的年利润最大为目标,效用函数为CDSO;IES 投资运营商以年成本最低为目标,IES 投资运营商m的效用函数为CIES,m。
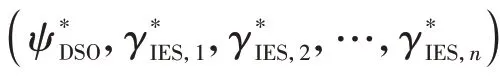
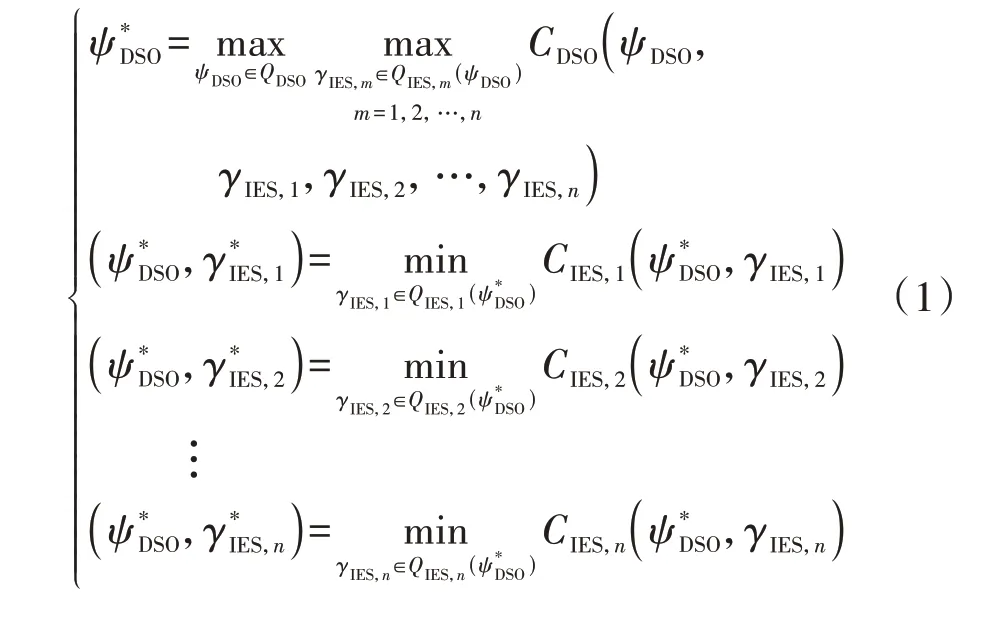
式中:QIES,m(ψDSO)表示当DSO 策略为ψDSO时,IES 投资运营商m的策略空间;QIES,1()、…、QIES,n)表示当DSO 策略取均衡解时,各IES 投资运营商的策略空间。
2.2 DSO规划模型
2.2.1 策略
DSO 随负荷新增和IES 的接入进行扩展规划,决策变量为线路、联络开关、变电站、变压器的投资变量以及各节点电价。
现有研究中DSO 向IES 售电时,均将电能视为同一品质属性的商品,忽略了供电可靠性要求对电价的影响。DSO 提供不同可靠性付出的成本不同,用户享受不同的可靠性服务应支付不同的费用,因此要考虑可靠性进行差异化定价。
本文采用一种考虑可靠性分量的电价定价方法,在原始电价ρ0的基础上叠加与可靠性相关的分量ρE,i,作为价格信号引导系统中所有参与者共同分担对用户的可靠性责任,则配电网中节点i处的电价ρi的表达式为:

参考根据可靠性对电力公司进行奖惩的协议PBR(Performance-Based Rate)制定可靠性分量。首先选定供电可靠率E作为可靠性指标,并对指标值划分出保留区(b*,c*),在保留区内既不奖励也不惩罚,可靠率低于保留区边界时对DSO 进行惩罚,高于保留区边界时对DSO进行奖励。
配电网供电成本随供电可靠性的提高而增大,在供电可靠性较小时,近似呈线性关系,在供电可靠性增加到一定水平后,近似呈指数增长,供电可靠性越高,增加单位可靠性提供的供电成本就越高[13]。由于本文中综合能源并网节点可靠性变化区间不大,因此对电价可靠性分量采用线性模型表示,如图2所示,其最大限值为ρE,max。
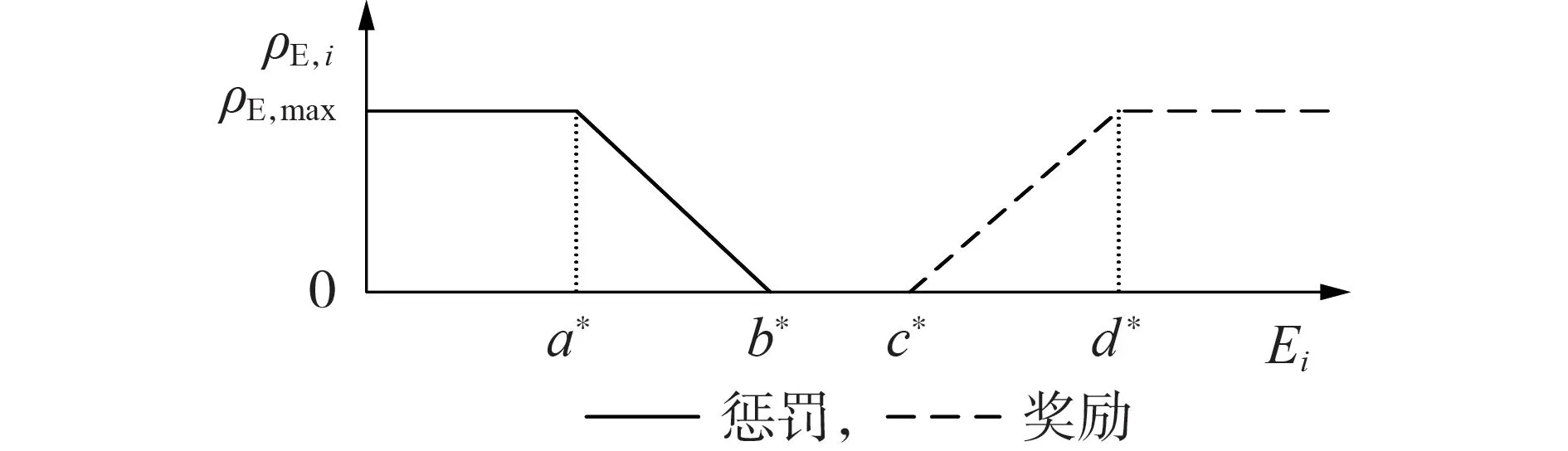
图2 电价可靠性分量奖惩曲线Fig.2 Reward and penalty curve of electricity price reliability component
2.2.2 效用函数
DSO以利润最大为目标,效用函数为:
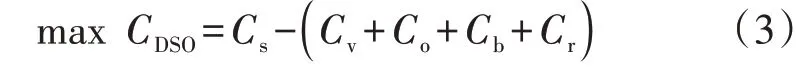
式中:Cs、Cv、Co、Cb、Cr分别为配电网扩展规划后的年售电收入、投资成本等年值、年维护成本、年购能成本和年网损成本。Co、Cr表达式见文献[14],其他变量计算公式如下:
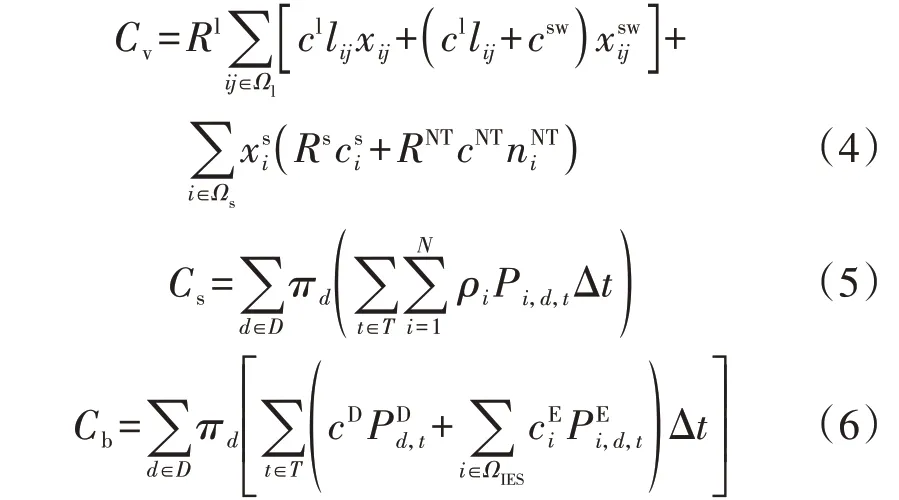
式中:Ωl为待选线路集合;Ωs为变电站节点集合;D为典型日集合;T为典型日的所有时段集合;cl、csw、、cNT分别为单位长度线路、联络开关、节点i处变电站扩容或新建、新增变压器的投资费用;lij为节点i与节点j间的线路长度;xij、分 别为节点i与 节点j间的线路、节点i与节点j间的联络开关、节点i处变电站投资变量,若取值为1 则表示投建,若取值为0 则表示不投建;nNTi为节点i处新增变压器数量;πd为一年中典型日d的累计天数;N为系统的节点数;Pi,d,t为配电网中典型日d的时段t内节点i处用户的购电量;Δt为一个调度周期,取1 h;ΩIES为新增IES节点集合分别为典型日d的时段t内配电网从上级电网和节点i处IES购电电量,cD、分别为相应的购电价格;Rl、Rs、RNT分别为线路、变电站、变压器的等年值因子[14]。
2.2.3 策略空间
DSO 的规划策略是首先在待选线路、待建变电站集合中取值,然后在网架方面要满足网络辐射状约束、连通性约束,最后在运行时要满足变电站容量约束、节点功率平衡约束、节点电压上下限约束、支路容量约束[15]。
1)网络辐射状约束。

式中:M为系统的支路数。2)网络连通性约束。
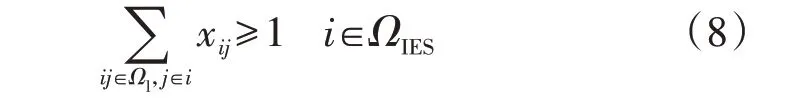
式中:j∈i表示节点j与节点i相连。
3)变电站容量约束。
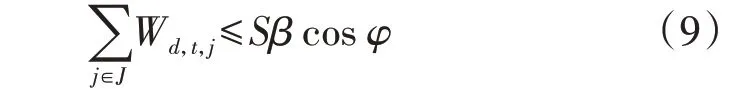
式中:J为变电站供电范围内的节点集合;Wd,t,j为节点j处变电站在典型日d的时段t内的用电功率;S、β、cosφ分别为变电站容量、负载率和功率因数。
2.3 IES投资运营商规划运行模型
2.3.1 策略
IES 投资运营商考虑终端负荷需求以及DSO 制定的电价对自身进行优化,其决策变量包括规划与运行变量。本文IES 考虑可能接入的设备种类为分布式光伏PV(distributed PhotoVoltaic)、燃气轮机GT(Gas Turbine)、燃气锅炉GB(Gas Boiler)、热泵HP(Heat Pump)、电制冷设备EC(Electrical Cooling)和吸收式制冷机AC(Absorption Chiller),并将所有IES统一建立为如附录A图A1所示结构的IES。
实际规划时不仅要考虑设备选型,还要确定相应台数,决策变量为离散变量,由于PV、HP 容量梯级变化较小,忽略不同型号设备容量变化对规划结果影响不大,故将其容量建模为连续变量,其余设备为离散变量,因此规划变量具体为PV、HP 设备的容量,GT、GB、EC、AC 设备的类型与台数,运行变量为各时段的机组出力和购电量、购气量。
2.3.2 效用函数
在DSO 给定电价的基础上,各IES 以总成本最小为目标,效用函数为:
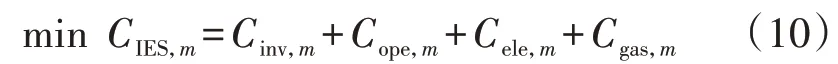
式中:下标m表示IES 投资运营商m;Cinv,m为投资成本等年值;Cope,m为年运维成本;Cele,m、Cgas,m分别为年购电、购气成本。
投资成本等年值表达式如下:
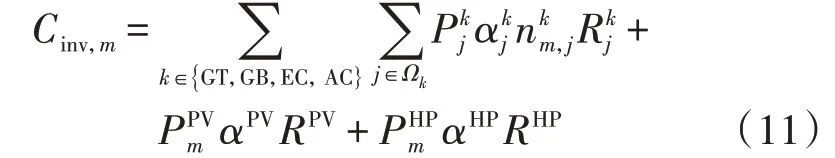
式中:Ωk为设备k(k∈{ G T,GB,EC,AC} )的待选类型集合;为类型为j的设备k的额定容量;分别为PV、HP 设备的安装容量、αPV、αHP分别为类型为j的设备k、PV、HP 设备的单位容量投资成本;为类型为j的设备k的安装台数、RPV、RHP分别为类型为j的设备k、PV、HP设备的等年值因子。
年运维成本表达式如下:
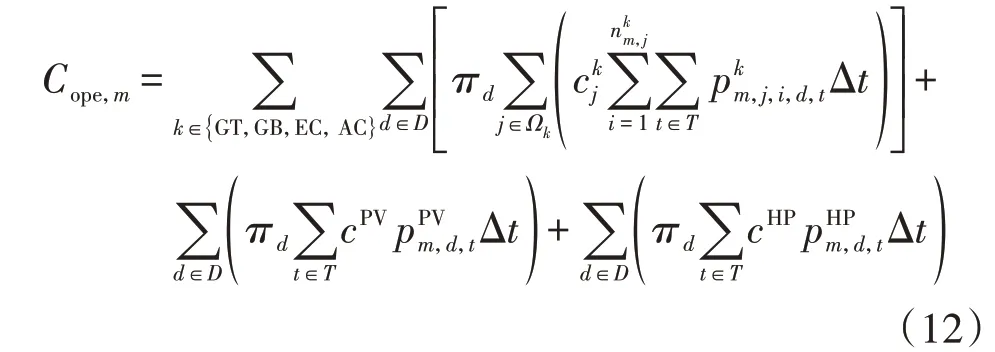
年购电、购气成本表达式分别如式(13)、(14)所示。IES投资运营商以运维、购能成本之和最小为目标制定运行策略。
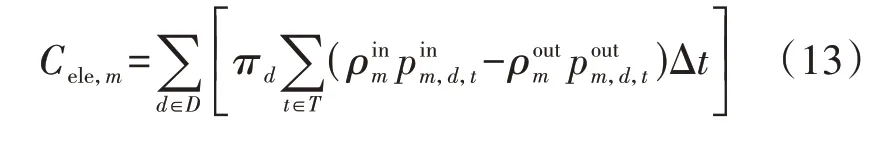
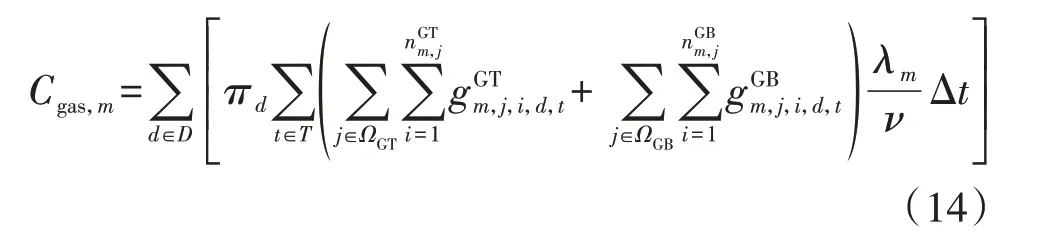
2.3.3 策略空间
IES投资运营商m的策略空间QIES,m包括规划和运行策略空间,规划策略空间由设备投资约束和可靠性约束组成,设备投资约束又分为离散设备和连续设备投资约束,运行策略空间由母线功率平衡约束和设备出力约束[16]组成,各类约束表达如下。
1)设备投资约束。
离散设备投资约束如下:
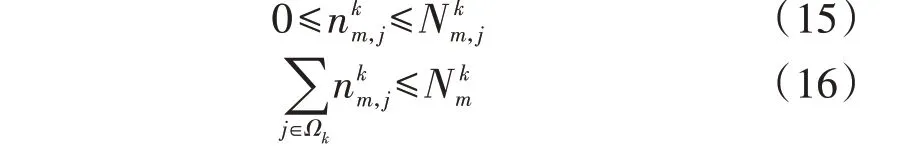
式中:k∈{G T,GB,EC,AC} ;j∈Ωk分别为各IES 中类型为j的离散设备k的安装台数上限和离散设备k的安装总台数上限。
连续设备投资约束如下:

2)可靠性约束。
利用供能可靠性约束可对规划方案进行可靠性校验,具体如下:
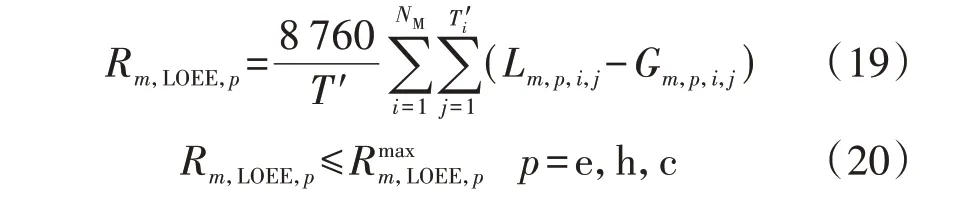
式中:T′为蒙特卡洛模拟时长;NM为抽样时段数;T′i为第i个抽样时段的故障时长;Lm,p,i,j和Gm,p,i,j分别为各IES在第i个抽样故障时段内第j小时下能源类型为p的负荷量和系统可供量;p=e,h,c 分别表示电、热、冷能源;Rm,LOEE,p和分别为各IES中能源类型为p的缺供能量期望和用户允许缺供量最大值。3)母线功率平衡约束。
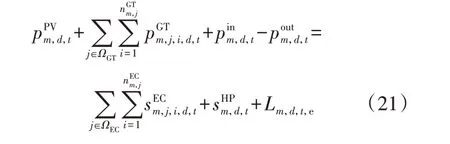
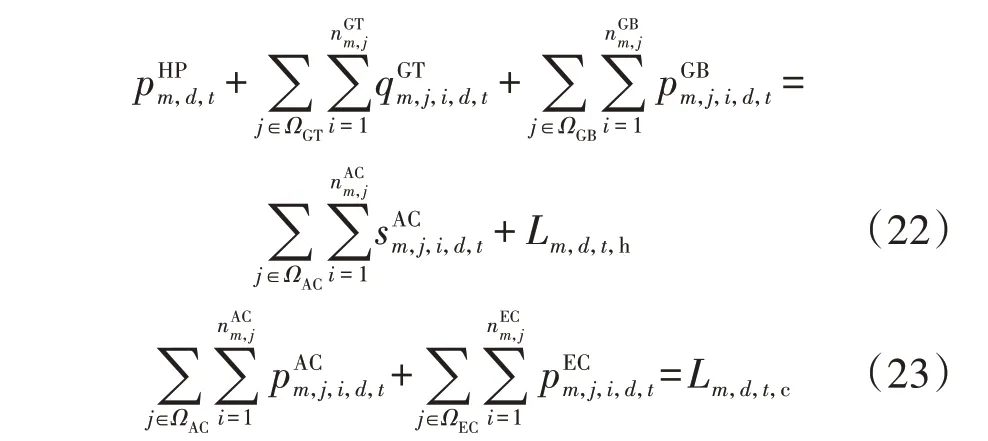
式中:d∈D;t∈T;分别为典型日d的时段t内各EC、AC 设备的输入电功率和热功率;为典型日d的时段t内HP 设备的输入电功率为典型日d的时段t内GT设备的输出热功率;Lm,d,t,e、Lm,d,t,h、Lm,d,t,c分别为典型日d的时段t内各IES 的电、热、冷负荷功率。
3 模型求解
主从博弈的特点在于博弈参与者地位不平等,领导者地位高于跟随者,优先制定决策,主从博弈问题呈现分层结构,上层领导者的决策变量被视为下层跟随者优化问题的已知参数,同时下层跟随者的优化问题是上层领导者优化问题的约束条件,相当于某类双层规划问题[17],均衡解的存在性与唯一性证明见附录B,模型结构如图3所示。
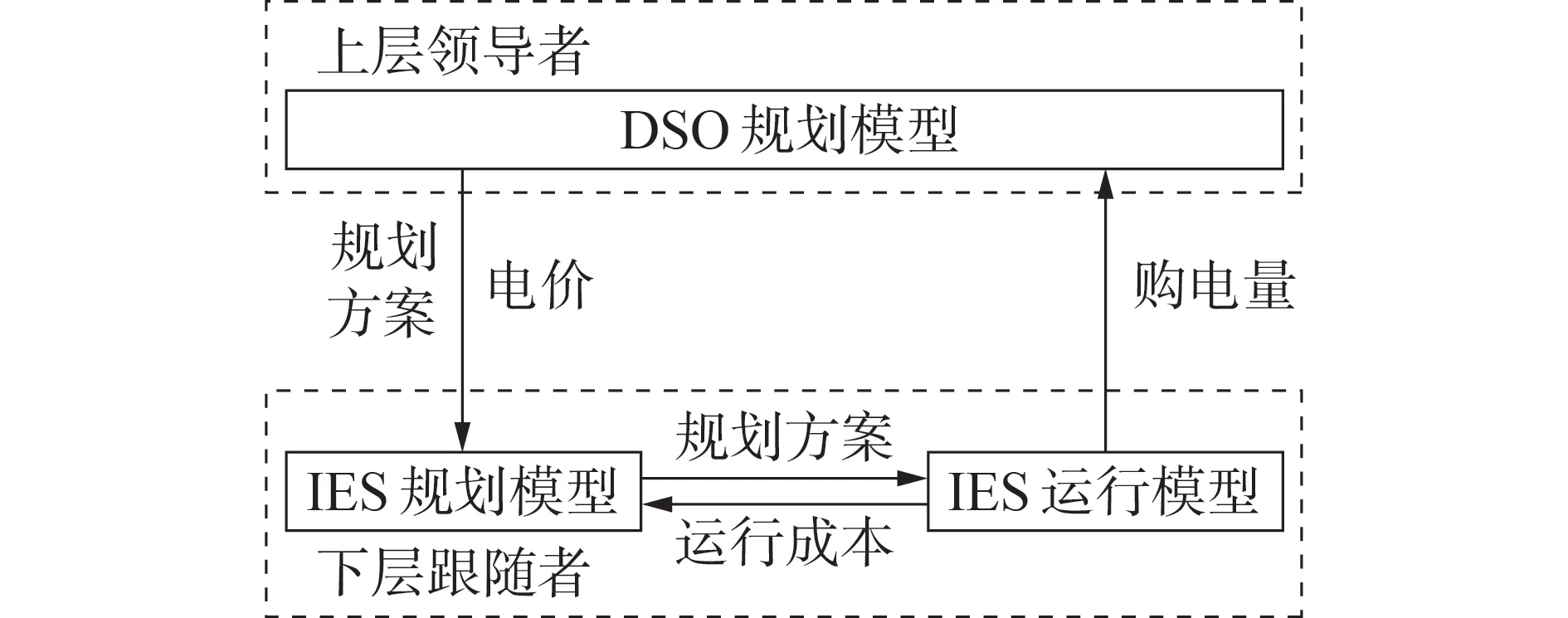
图3 模型结构Fig.3 Model structure
图3中:DSO 规划模型和IES规划模型均为混合整数非线性规划模型,可采用差分进化算法进行求解;IES运行模型为线性规划模型,可采用OPTI求解器进行求解,具体求解流程如附录C图C1所示。
4 算例分析
4.1 基本数据
本文采用改进的IEEE 14 节点配电网系统进行算例分析,系统结构如图4 所示。图中:节点1 为已有变电站节点,与上级电网相连;节点2—14为已有负荷节点;节点15—17分别为新增居民类、商业类、工业类3个IES节点;节点18为待建变电站节点。
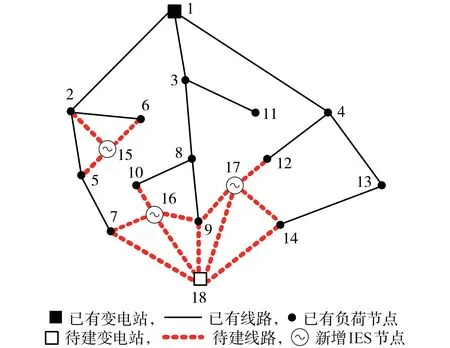
图4 仿真系统结构图Fig.4 Structure diagram of simulation system
系统电压基准值VB=20 kV,节点电压上、下限分别设为1.07VB和0.93VB,已有变电站中有1台额定容量为7.5 MV·A 的变压器。本文选取4 个典型日,其中夏季极端日白天光辐射强度较小,负荷同夏季典型日。各典型日在一年中的累计天数、光辐射强度分别如附录C表C1、图C2所示。
DSO 从上级电网购电电价为0.15 元/(kW·h),向IES 售电原始电价为0.4 元/(kW·h),IES 向配电网售电电价为相应购电电价的70%[18];IES 中待配置设备参数如附录C表C2—C5所示。
4.2 计算结果分析
将各IES 用户允许缺供量最大值设为年负荷的7.5%,DSO定价参数中奖惩区间参数a*、b*、c*、d*分别设置为0.799 65、0.999 65、0.999 90、0.999 99,ρE,max取值在0.1~0.5 元/(kW·h)范围内,求解可得当ρE,max为0.201 元/(kW·h)时,主从博弈达到均衡,DSO 的扩展规划策略为新建线路15-2、16-10、17-12,新增节点15—17 的并网点可靠性分别为88.598 6%、82.724 4%、88.955 3%,电价分别为0.286 3、0.227 6、0.289 9 元/(kW·h),各节点IES 规划结果如附录C表C6所示。
4.3 不同规划方法的对比分析
为充分分析采用主从博弈方法对DSO 和IES 投资运营商规划结果以及整体供能成本的影响,本文设置以下2种场景进行对比分析:场景1,配电网-多IES独立规划;场景2,基于主从博弈的协调规划。
2 种场景下各IES 投资运营商的各项成本对比如图5 所示,图中运行成本为维护成本、年购电和购气成本之和。可以看出,3 个IES 各项成本变化趋势基本一致,采用主从博弈方法使3个IES投资成本分别增加了42.64、54.96、72.52 万元,主要由EC、GT 配置增加引起的,增强了多能耦合,说明IES 分担的可靠性责任增大,但由于购能成本大幅降低,使运行成本分别减小了57.39、134.35、177.22 万元,总成本分别减小了14.75、79.39、104.7万元。
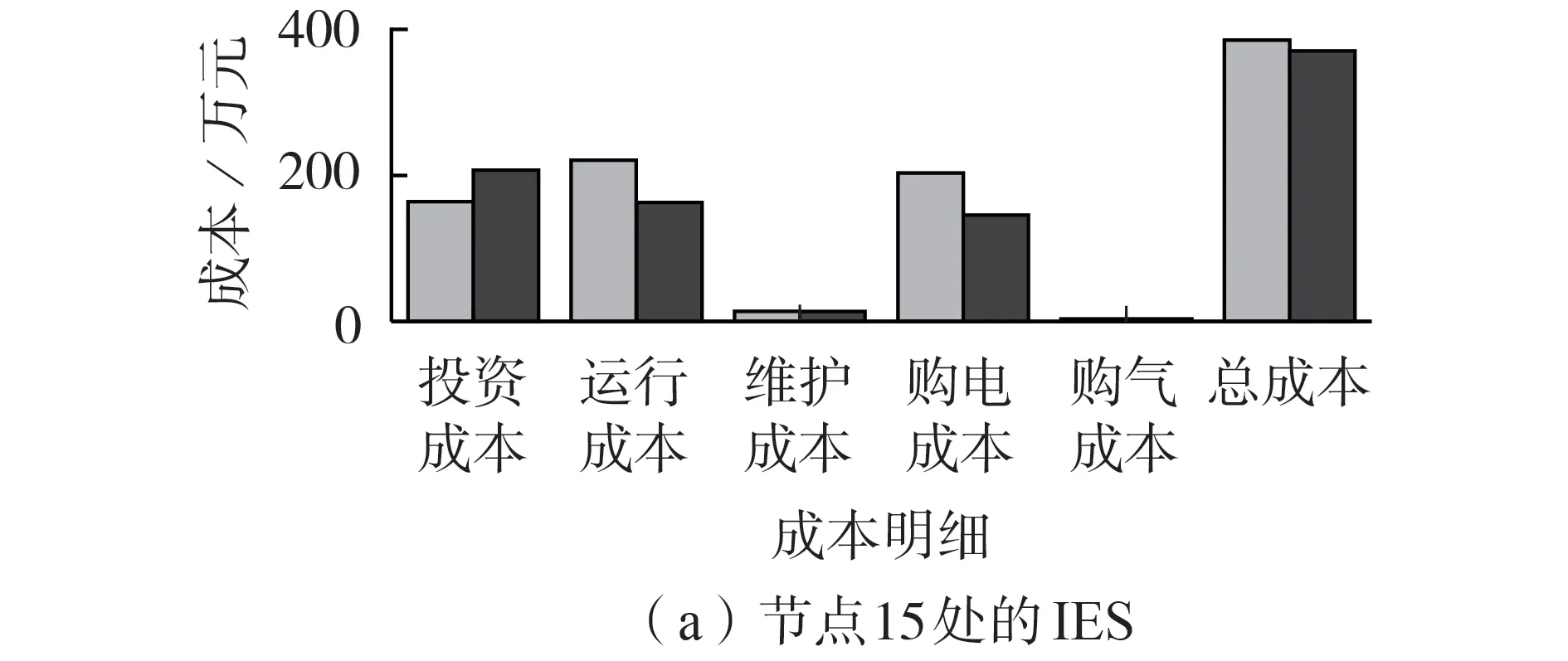
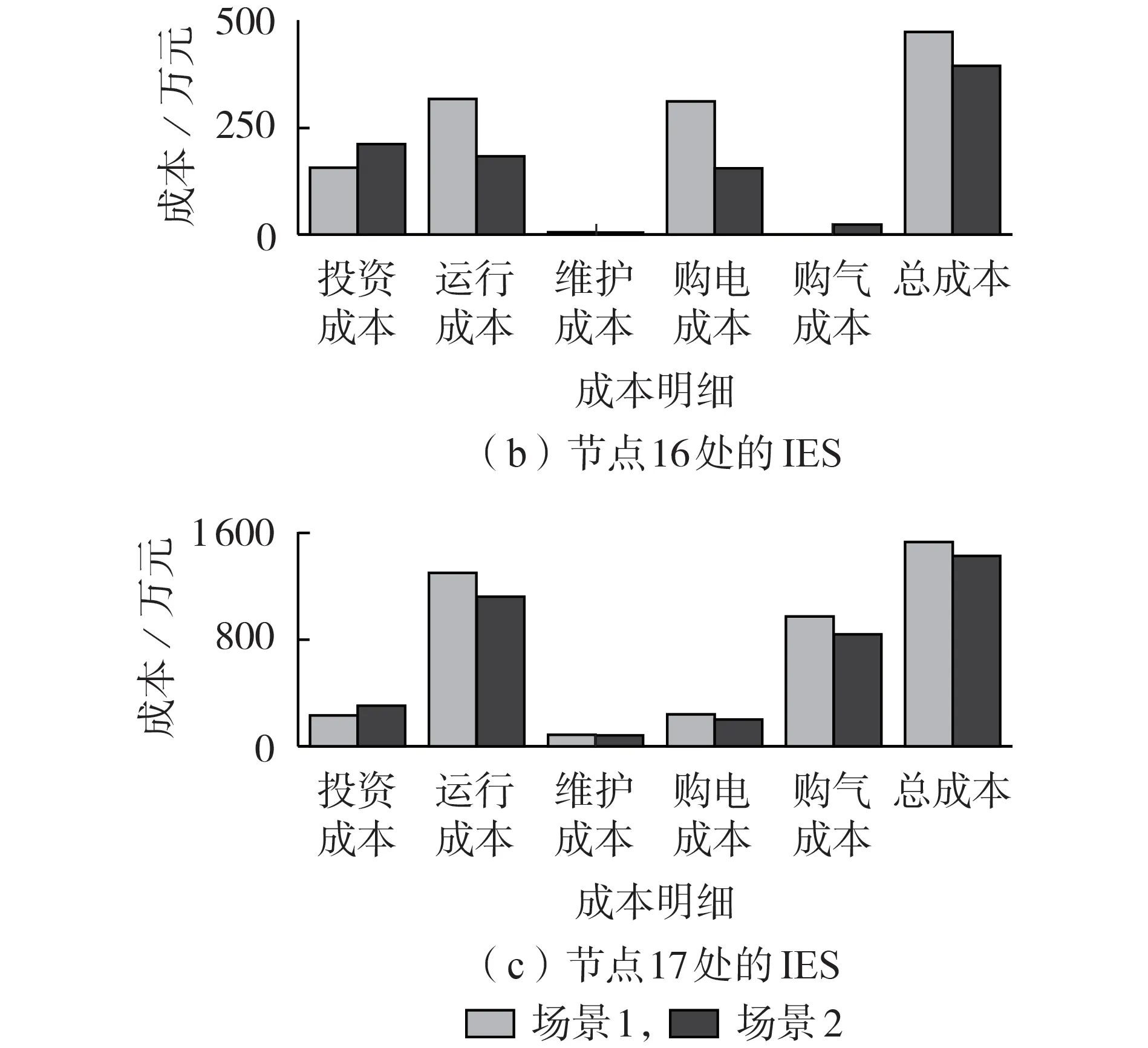
图5 各节点处的IES投资运营商成本明细Fig.5 Cost details of IES operator at each node
DSO 各项费用对比如表1 所示。可以看出,采用主从博弈方法后,DSO 售电量减小,且电价降低,导致售电利润减小了9.76 万元,但由于线路和变电站容量配置减小,配电网投资成本大幅降低,年利润提高了58.72 万元。这说明用户对配电网可靠性的依赖程度降低,减少了配电网可靠性责任。

表1 DSO各项费用对比Table 1 Comparison of expenses for DSO
为分析不同规划方法对配电网和IES 整体供能成本的影响,将2 种场景下整体供能成本明细进行对比,如表2 所示,表中总投资成本、年维护总成本分别为DSO与3个新增IES的投资成本、年维护成本之和,年外购能源成本为DSO 从上级电网年购电成本与3 个新增IES 从天然气网络年购气成本之和。对比可知,场景2 相比场景1 虽然总投资成本等年值增加了104.27 万元,但维护总成本、网损成本、年外购能源成本分别减小了8.55、0.001、120.22 万元,总供能成本减小了24.49万元,这说明采用主从博弈协调规划方法能降低整体供能成本。
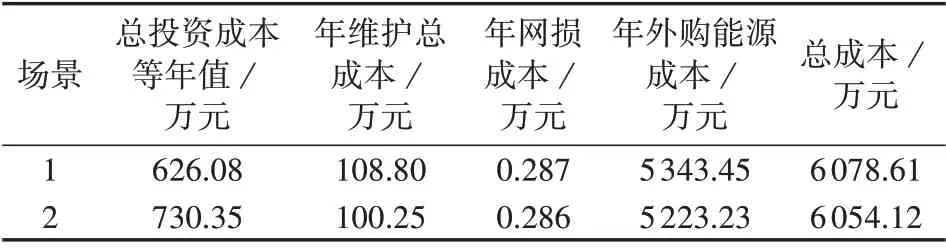
表2 整体供能成本明细Table 2 Cost details of overall energy supply
相比独立规划方法,采用主从博弈方法相当于将DSO 的部分可靠性责任向IES 运营商转移,实现了将对用户供能可靠性的责任在DSO 和IES 投资运营商之间的合理分摊,同时提升了双方的经济效益,且有效降低了整体供能成本,具有重要的社会价值。
4.4 用户可靠性要求对博弈结果的影响
为了分析新增IES 终端用户的可靠性要求对博弈结果的影响,分别设置各节点用户允许缺供量最大值占年负荷比例在2.5%~25%范围内,其余参数不变,采用本文方法对DSO 和IES 双方进行优化,可得到在用户不同可靠性要求下DSO 与各IES 的投资成本变化情况分别如附录C图C3、C4所示。可以看出,当用户允许缺供量最大值占年负荷比例在2.5%~12.5%范围内时,随着用户对可靠性要求的提高,DSO 投资成本逐渐减小,IES 投资成本大幅增加,这说明在用户对供能可靠性要求较高的范围内,随着用户对可靠性要求的提高,DSO 分担的可靠性责任逐渐降低,IES分担的可靠性责任逐渐提高。这是因为当用户的可靠性要求较高时,配电网增加投资主要带来供电可靠性的提升,对供热/冷可靠性的提升影响较小,配电网增加巨额的投资,也只能带来较小的可靠性增量,为满足用户提高的供热/冷可靠性要求,IES 需要增加设备配置,从而使得生产能力增强,外购电量大幅减小,DSO 售电收入减小,只能通过减少投资提高利润。
当用户允许缺供量最大值占年负荷比例在12.5%~25%的范围内时,随着用户对可靠性要求的降低,DSO 投资成本逐渐减小,在12.5%~20%的范围内IES投资成本基本不变,在20%~25%的范围内IES 投资成本逐渐减小。这是因为用户对供能可靠性的要求较低,双方只需承担较小的可靠性责任就能满足用户需求,适当减小设备配置更有利于提高经济性。
2种场景下配电网与IES总供能成本随用户可靠性要求的变化曲线如图6所示。可以看出,2种场景下总供能成本均随用户可靠性要求的提高而增大,主要是由投资成本的变化引起的。另外,随着用户可靠性要求的提高,2 种场景下总供能成本的差值逐渐增大,且场景2 始终低于场景1,这说明随着用户可靠性要求的提高,采用主从博弈协调规划方法在降低配电网和IES整体供能成本方面的效果越显著。
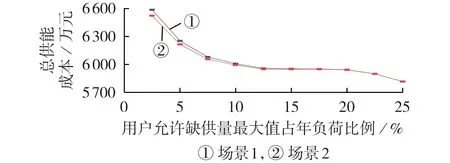
图6 总供能成本随用户可靠性要求的变化曲线Fig.6 Curve of overall energy supply cost vs.user reliability requirement
5 结论
本文提出了基于主从博弈的配电网-多IES 协调规划模型,通过算例分析验证了模型的有效性,得到以下结论:
1)采用主从博弈协调规划方法虽增加了IES 投资成本,但使购能成本减小,总成本降低,且能大幅降低DSO 投资成本,延缓电网投资,同时提升了双方的经济效益;
2)利用电价引导可靠性投资,能更好地协调经济性与可靠性间的矛盾,实现对IES 用户供能可靠性责任在DSO 和IES 运营商之间的合理分摊,充分利用IES潜在的可靠性价值,降低了整体供能成本;
3)IES 用户的可靠性要求不同会影响可靠性责任在DSO 和IES 之间的分摊和最优投资的制定,本文所提方法能帮助双方根据不同用户实际可靠性要求制定最佳规划方案,且用户的可靠性要求越高,降低整体供能成本的效果越显著。
附录见本刊网络版(http://www.epae.cn)。
