缺失数据下空气质量预测的ARIMA乘法季节模型

田文婷，宇世航

缺失数据下空气质量预测的ARIMA乘法季节模型

田文婷，宇世航

（齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161000）

以AQI指数作为评判空气质量状况的标准进行探究，对存在缺失值的AQI指数进行填充，经探究发现，填充后的AQI指数存在明显季节特征，提出在原ARIMA模型上加入季节特征，建立ARIMA乘法季节模型。首先选东北四个城市进行实证分析，用均值法和缺失森林法对缺失数据进行填充，依据存在的季节特征分别建立适当的ARIMA乘法季节模型，对未来12个月空气质量进行预测并拟合未来变化趋势，将预测的数据与真实数据进行对比，得出ARIMA乘法季节模型在预测空气质量时优于单纯的ARIMA模型，使用缺失森林填充后建立的ARIMA乘法季节模型优于用均值法填充。最后，确定基于缺失森林填充的缺失数据建立的ARIMA乘法季节模型为较优的预测模型。

AQI指数；缺失森林；季节性；ARIMA乘法季节模型

目前，环境问题日益显著，从国家长远发展来看，环境问题必须解决。近来，诸多城市出现雾霾天气，空气污染问题迫在眉睫，为解决环境问题，我国出台了很多相应政策。目前，有多位学者就环境问题、空气质量问题进行了多方面的探究，以便提供合理的建议。余晓美[1]，孙铭[2]，孔朝莉[3]，王雪娇[4]，王未来[5]等学者探究了空气质量的变化特征；严宙宁[6]，黄珊[7]等学者对空气质量进行预测，肖悦[8]等对空气质量的空间分布特征进行探究。先前学者均是基于数据完整的前提下提出的，但实际生活中，收集到的数据并非完整数据，可能存在缺失值。对于存在缺失值的数据，若直接删除数据将会导致预测模型产生较大误差，因此如何构建预测模型至关重要。

1 数据来源

本文数据主要来源于中华人民共和国生态环境部，部分数据来源于http://www.tianqihoubao.com/。选取了2013年5月到2020年4月的大连市、沈阳市、哈尔滨市、长春市AQI指数的月度数据，对数据中存在的缺失值本文采取两种处理方法。根据填充后的数据进行分析，文章中进行的数据分析均采用R语言[9-10]实现。

2 填补方法

本文对选取的数据集进行缺失值处理，主要采用了均值填补法和缺失森林填充。均值填补是最常用的缺失值处理方法，其核心是用未缺失的数据均值代替其缺失值，因均值本身受异常值影响较大，使用该方法填充存在较大误差。缺失森林[11]填补是利用随机森林填充缺失值的非参数方法，其先是将缺失值从少到多进行排序，用随机森林回归填补缺失值最少的，然后不断进行迭代即可得到填充后的数据，因缺失森林主要利用回归进行填补，所以该方法存在的缺点是可能存在过拟合。

3 模型介绍

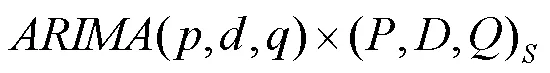
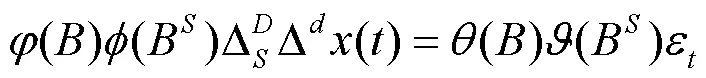
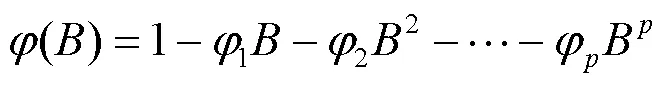
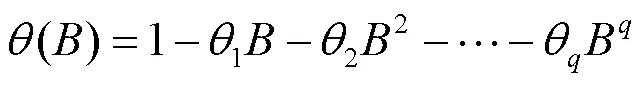
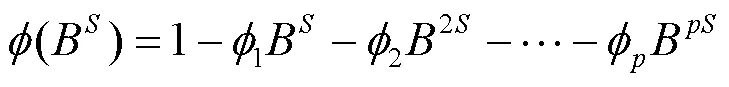
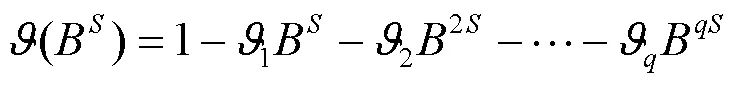
4 实证分析

4.1 缺失值处理

为进行建模，对选取的空气质量数据进行缺失值处理，其缺失值情况如图1所示。

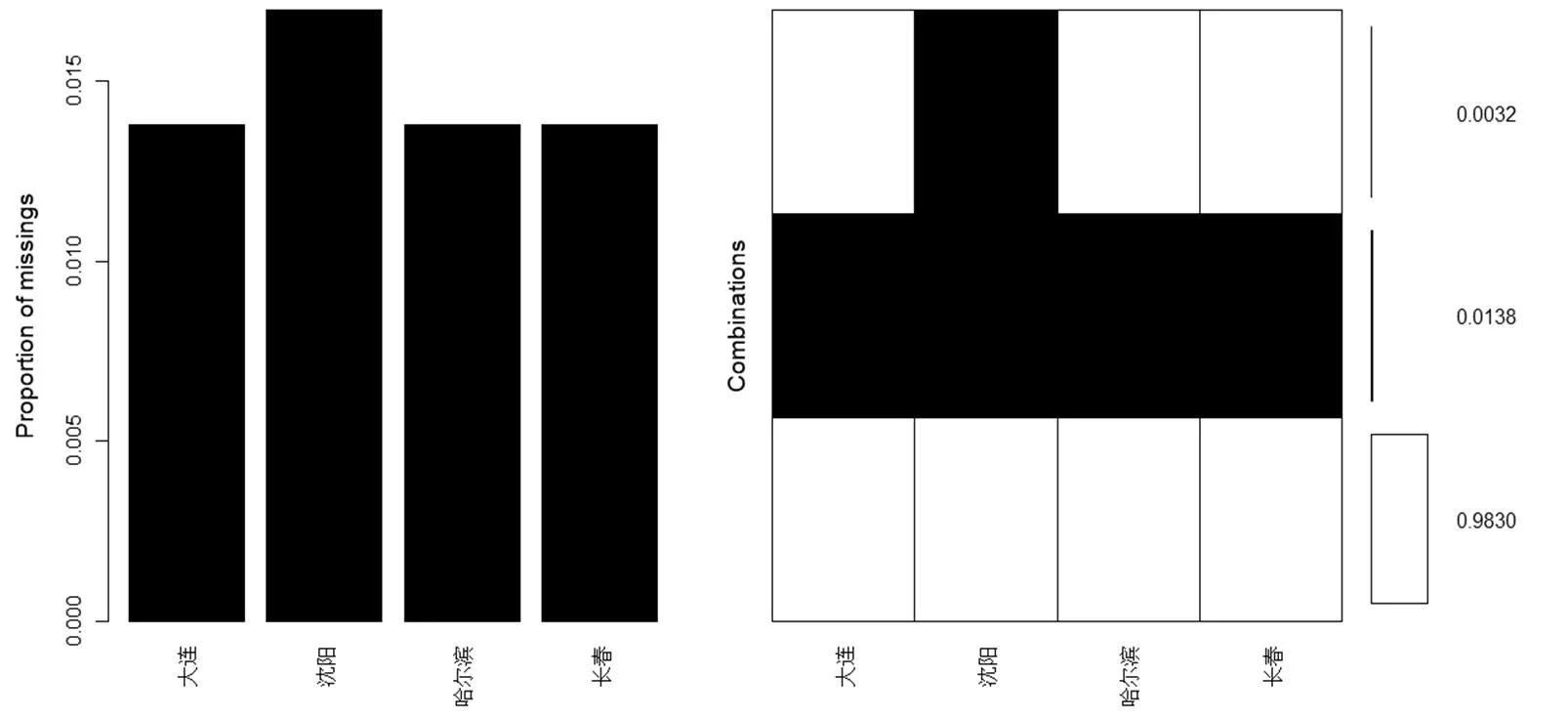
图1 四个城市数据缺失率

图1中，大连市、哈尔滨市以及长春市的缺失率均为0.0138，而沈阳市的缺失率达到了0.0170。对缺失数据分别采用均值法和缺失森林进行填补，后续建立ARIMA乘法季节均依据填补后的数据，下文中出现的绘制图均依据于缺失森林填补的数据。

4.2 绘制各个城市的曲线图

为探究AQI指数的变化特征，根据选取的大连市、沈阳市、哈尔滨市以及长春市2013年5月到2019年12月的AQI指数数据绘制趋势图如图2所示。

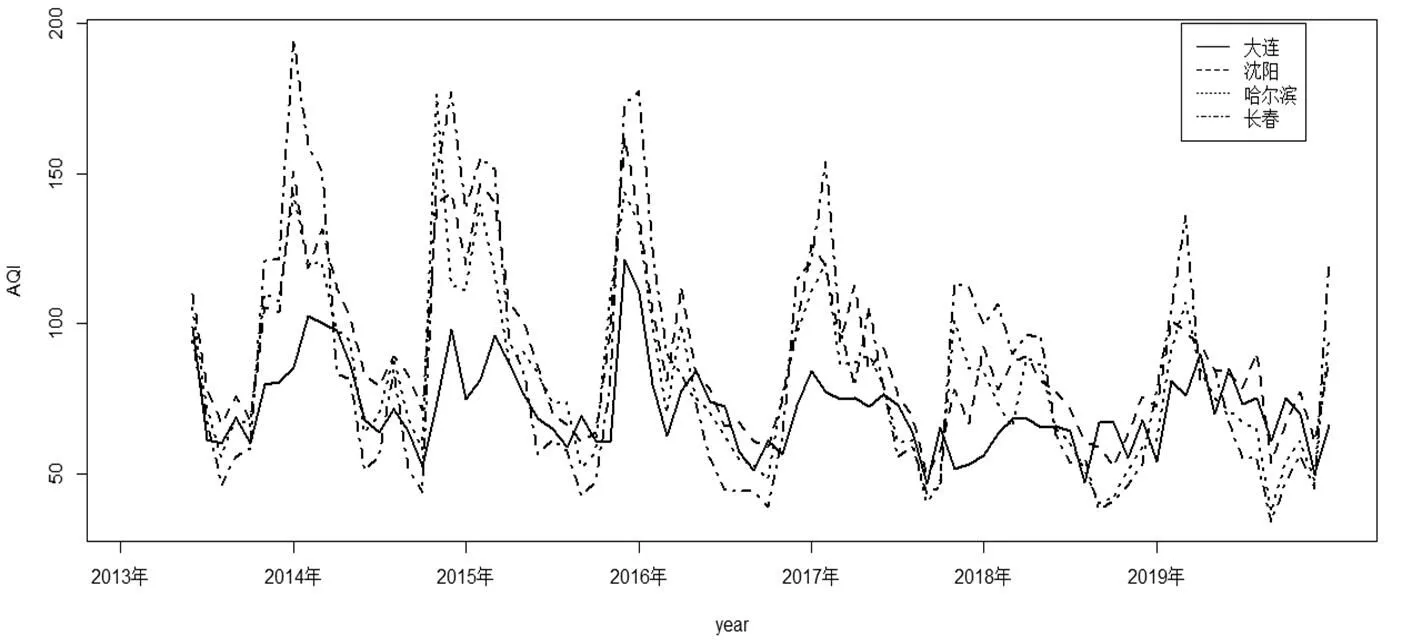
图2 AQI指数趋势图

如图所示：（1）东北地区四个城市的AQI指数曲线呈现出季节变化特征。从2013年5月到2019年12月，每年呈现三个变化过程，第一个过程为下降阶段，大约为每年一月到五月份，第二个过程为小幅波动过程，平稳期大约为每年六月到九月左右，第三过程为急剧上升过程，大约为每年的十月到十二月。全年AQI的峰值基本出现在每年的冬季，出现这一现象的原因为东北地区依靠燃烧煤炭、秸秆等燃料进行取暖，造成AQI指数增大，空气污染严重。

（2）4个城市中AQI指数曲线存在差异。图2中可知大连市的AQI指数曲线不同于其他城市，相比之下，大连市AQI指数在各个季节变化较小。相反，长春市在各个季节变化较大。出现该现象的原因与其城市所在的地理位置，经济发展水平及主要特征等因素有关。

4.3 平稳性检验及相关性检验

4.3.1 平稳性检验

各个城市AQI指数数据呈现明显周期性，且具有不显著向下的趋势性，为消除时间趋势项，进行一阶差分得到新序列，对新序列进行平稳性检验，检验结果如表1所示。取显著性水平为0.05时，ADF检验的P值均小于0.05，说明拒绝原假设，接受备择假设，即不存在单位根，认为差分后序列是平稳的，故本文中选取=1,=1, 构造预测模型。

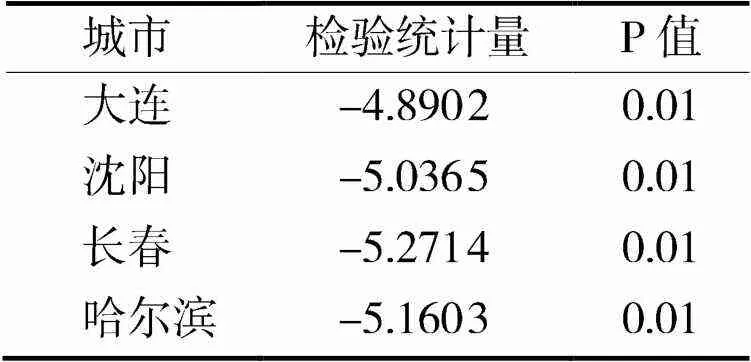
表1 ADF检验表

4.3.2 相关性检验

根据各个城市的AQI指数绘制其自相关图3所示。

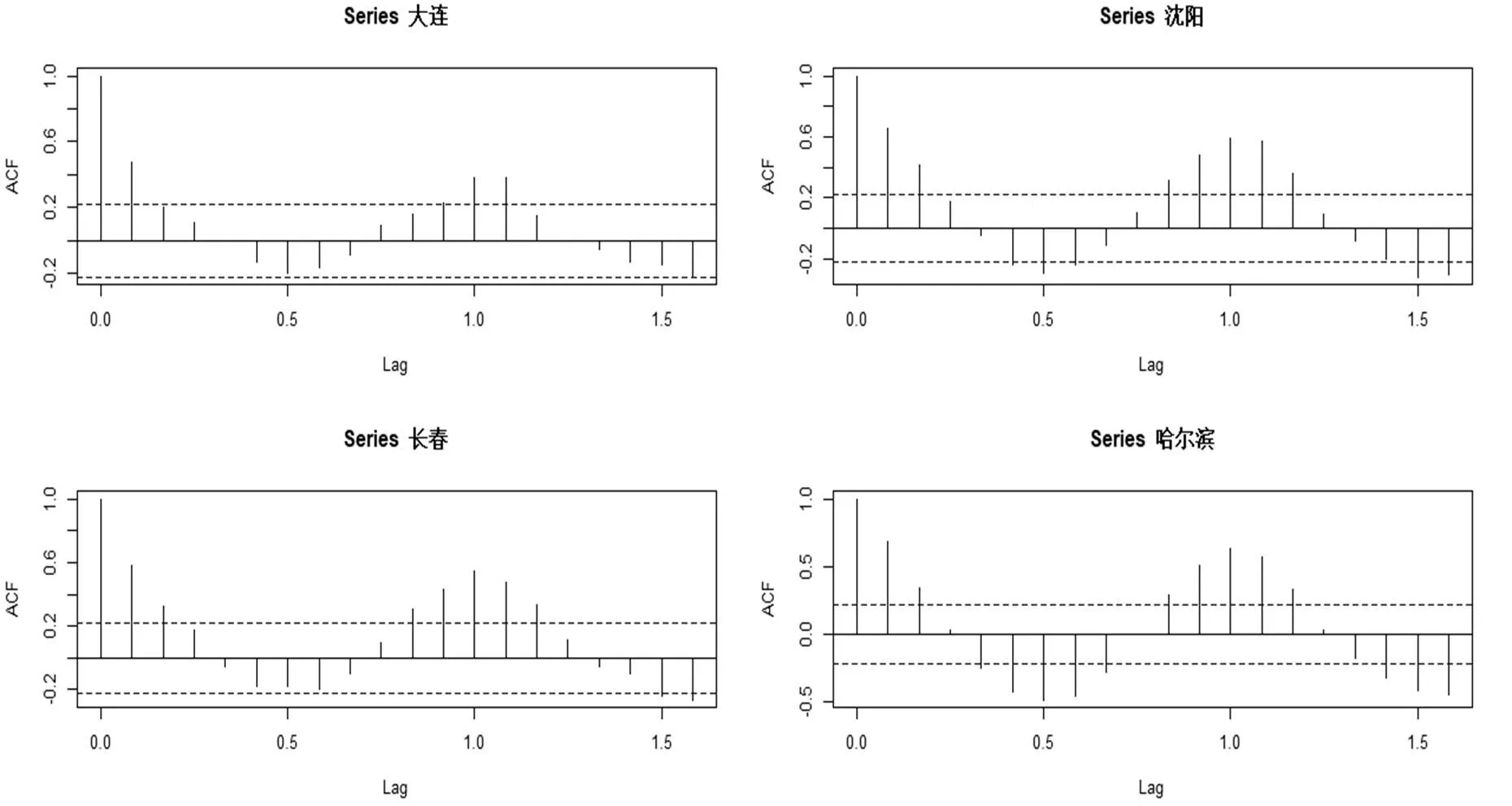
图3 原始数据自相关图

如图3所示：各个城市的AQI指数存在明显季节特征，根据自相关图显示，自相关函数之间存在较强的相关关系，故进行季节差分，消除季节趋势，使序列变为平稳时间序列。

4.4 预测模型建立

4.4.1 大连市预测模型

根据大连市2013年5月到2019年12月的AQI指数数据建立预测模型，为建立较优的模型，建立了多个模型对比得表2。

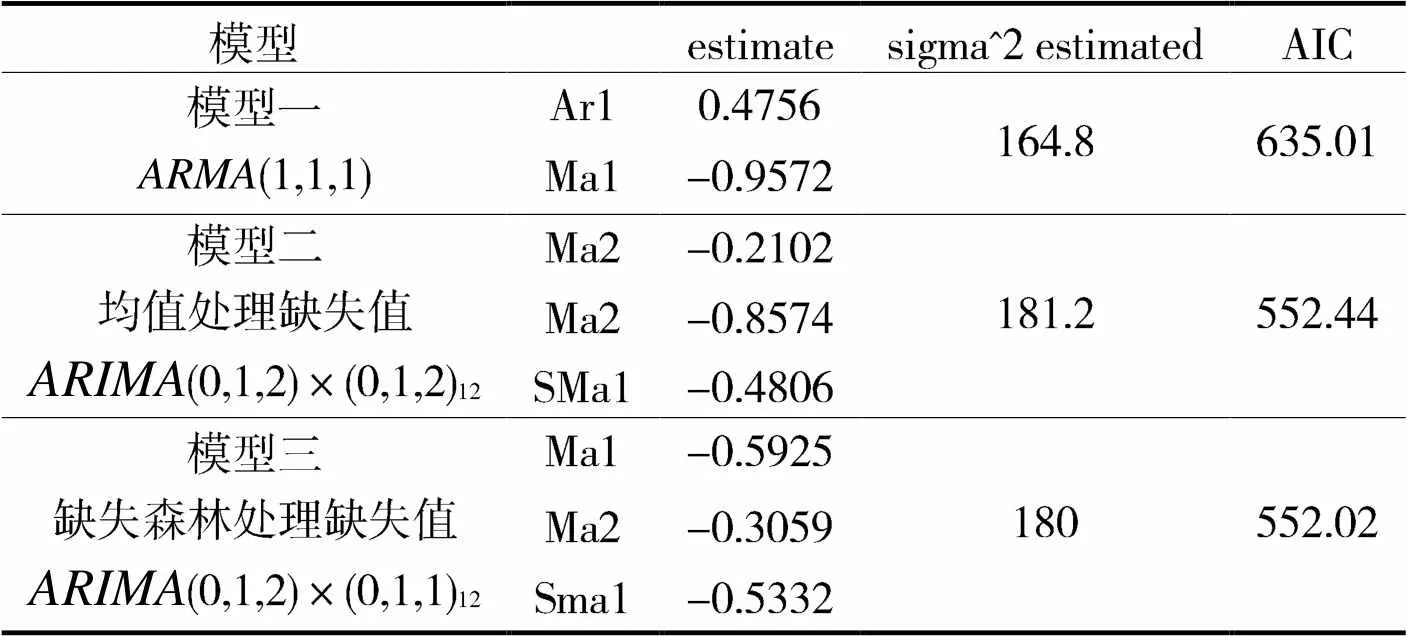
表2 大连市预测模型表

如表2所示：模型一为传统的时间序列模型，其建立依据于均值处理缺失值数据，不含季节性，此时其AIC的值为635.01，当将数据的季节性考虑进去时，建立模型二，其AIC的值明显减小，当采用缺失森林填充数据时，建立了模型三时，其AIC的值变成552.02，略有减小，故此时选择模型三。对模型三残差序列绘制自相关图和偏自相关图，其并无显著自相关，故该模型是充分的，模型的表达式为

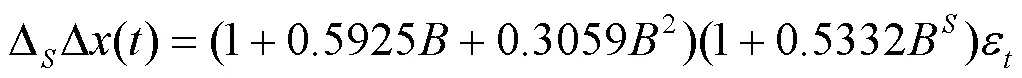
将=12带入上式即可得模型表达式，进一步对该模型的残差序列进行Box-Ljung检验，检验结果中P值为0.9123大于显著性水平0.05，故接受原假设，认为残差序列为白噪声。与传统模型相比，加入季节乘法模型后其AIC显著减小。

4.4.2 沈阳市预测模型

根据沈阳市2013年5月到2019年12月的AQI指数数据建立预测模型，为建立较优的模型，建立多个模型对比得表3。

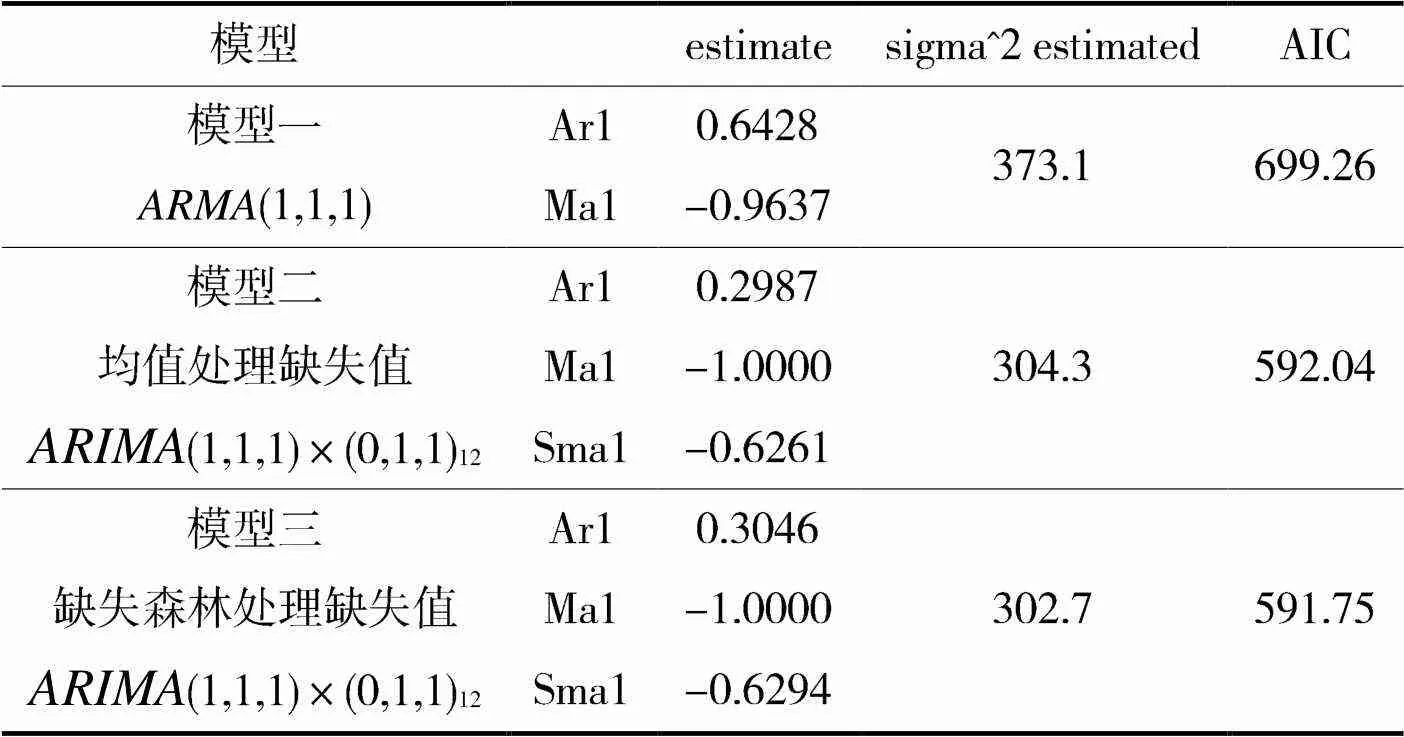
表3 沈阳市预测模型表

如表3所示，模型一是传统的模型预测方法，即不含季节乘法模型的ARIMA模型，其数据依据于均值填充的数据，模型的AIC为699.26，在此模型的基础上加入季节乘法项，其AIC减小为592.04，AIC的值显著减小，将原数据使用缺失森林填充，再依据该数据建立ARIMA乘法季节模型三，其AIC的值继续减小。为检验模型三是否充分，绘制残差序列的自相关图和偏自相关图，其并无显著关系中系数显著，所以该模型是充分的，模型的表达式为

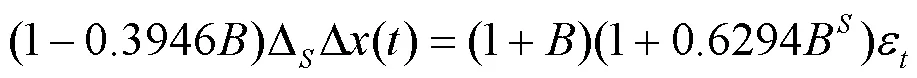
将=12带入上述模型即得到预测模型，进一步对该模型的残差序列进行Box-Ljung检验，检验结果中P值为0.9068大于显著性水平0.05，故接受原假设，认为残差序列为白噪声。

4.4.3 长春市预测模型

根据长春市2013年5月到2019年12月的AQI指数数据建立预测模型，为建立较优的模型，建立多个模型对比得表4。

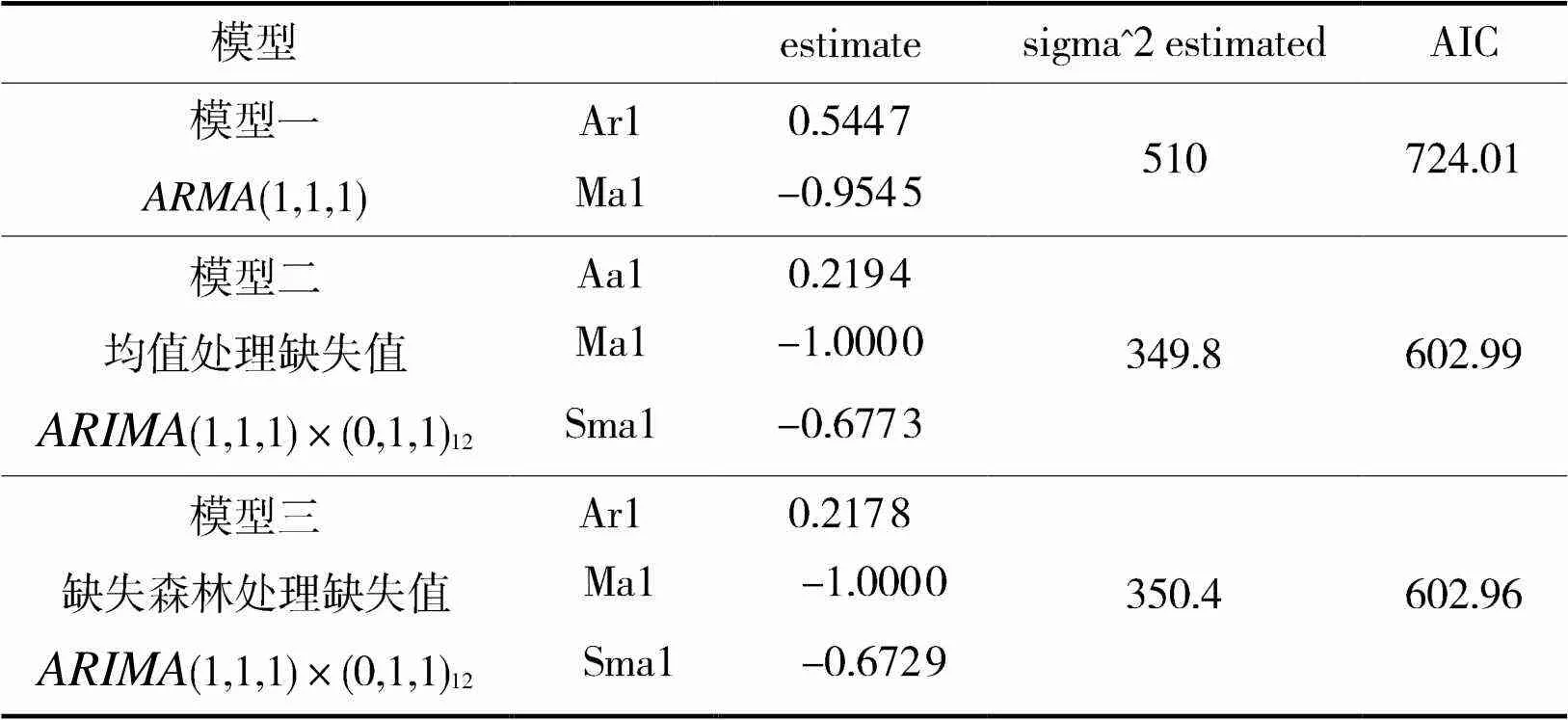
表4 长春市预测模型表

如表4所示：模型一使用了均值填充缺失值的数据，建立了不含季节项的(1,1,1)，其AIC的值为724.01，当给模型一加入季节乘法项时，得到模型二，其AIC显著降低，降低到602.99，进一步探究，采用缺失森林填补缺失值时，建立了模型三，与前两个模型相比，AIC的值降低，其值为602.96。在模型三中取显著性水平为0.05时，所有系数均显著，该模型的残差序列的自相关图和偏自相关图都没有显著的自相关，所以该模型是充分，模型的表达式为

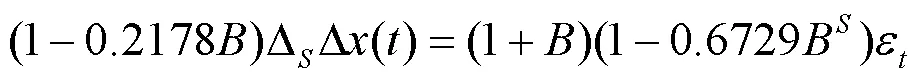
将=12带入上述模型得到长春市预测模型，进一步对该模型的残差序列进行Box-Ljung检验，检验结果中P值为0.7649大于显著性水平0.05，故接受原假设，认为残差序列为白噪声。

4.4.4 哈尔滨市预测模型

根据哈尔滨市2013年5月到2019年12月的AQI指数数据建立预测模型，为建立较优的模型，建立多个模型对比得表5。

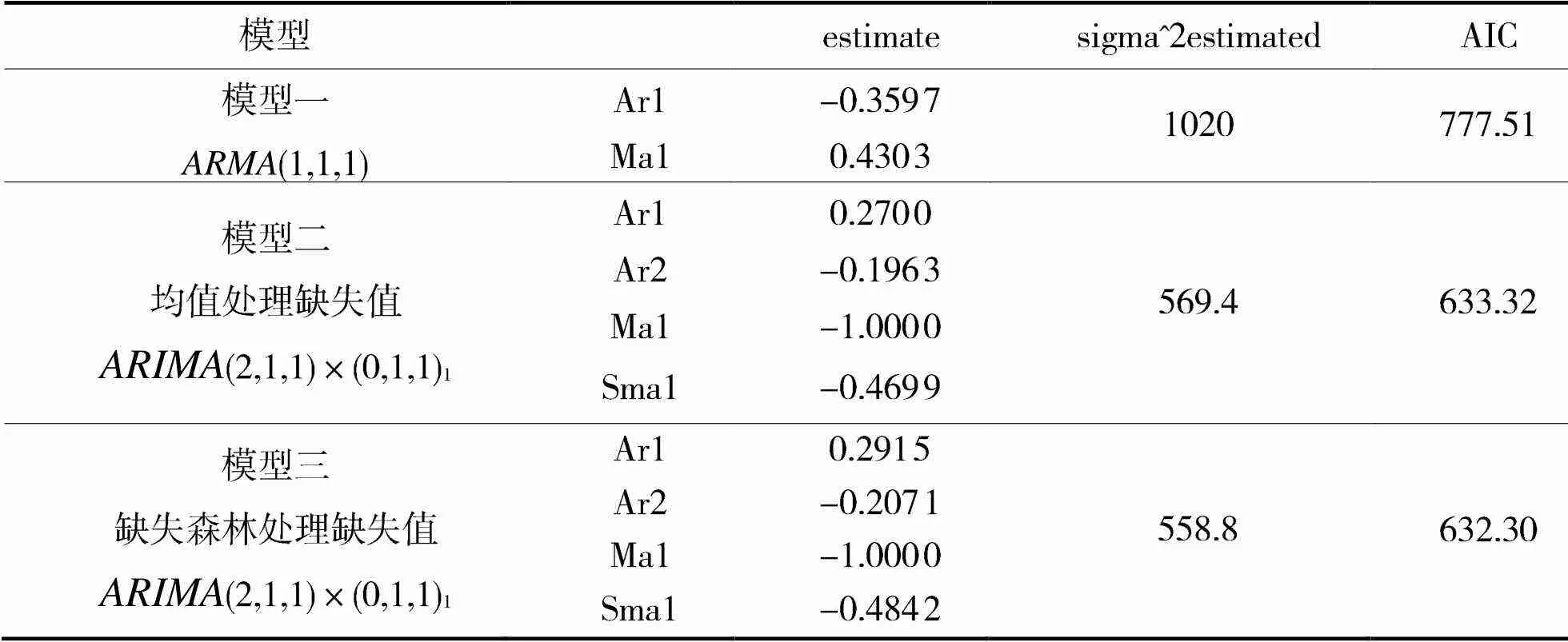
表5 哈尔滨市预测模型表

如表5所示：模型一为不含有季节效应的模型，其AIC的值为777.51，在模型一的基础上增加季节模型并进行修正，得到模型二，模型二的AIC显著降低。同理，将原始数据使用缺失森林进行填充，然后建立模型三，绘制模型三的自相关和偏自相关图可知，该模型的残差序列的自相关图和偏自相关图不存在显著的相关性所以该模型是充分，模型的表达式为

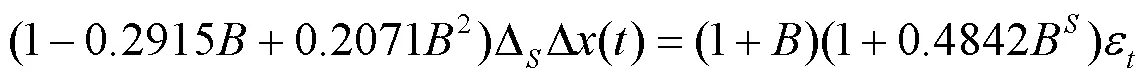
进一步对该模型的残差序列进行Box-Ljung检验，检验结果中P值为0.6437大于显著性水平0.05，故接受原假设，认为残差序列为白噪声。

4.5 残差序列相关图检验

根据上述模型中，绘制相应的自相关图与偏自相关图如图4所示。

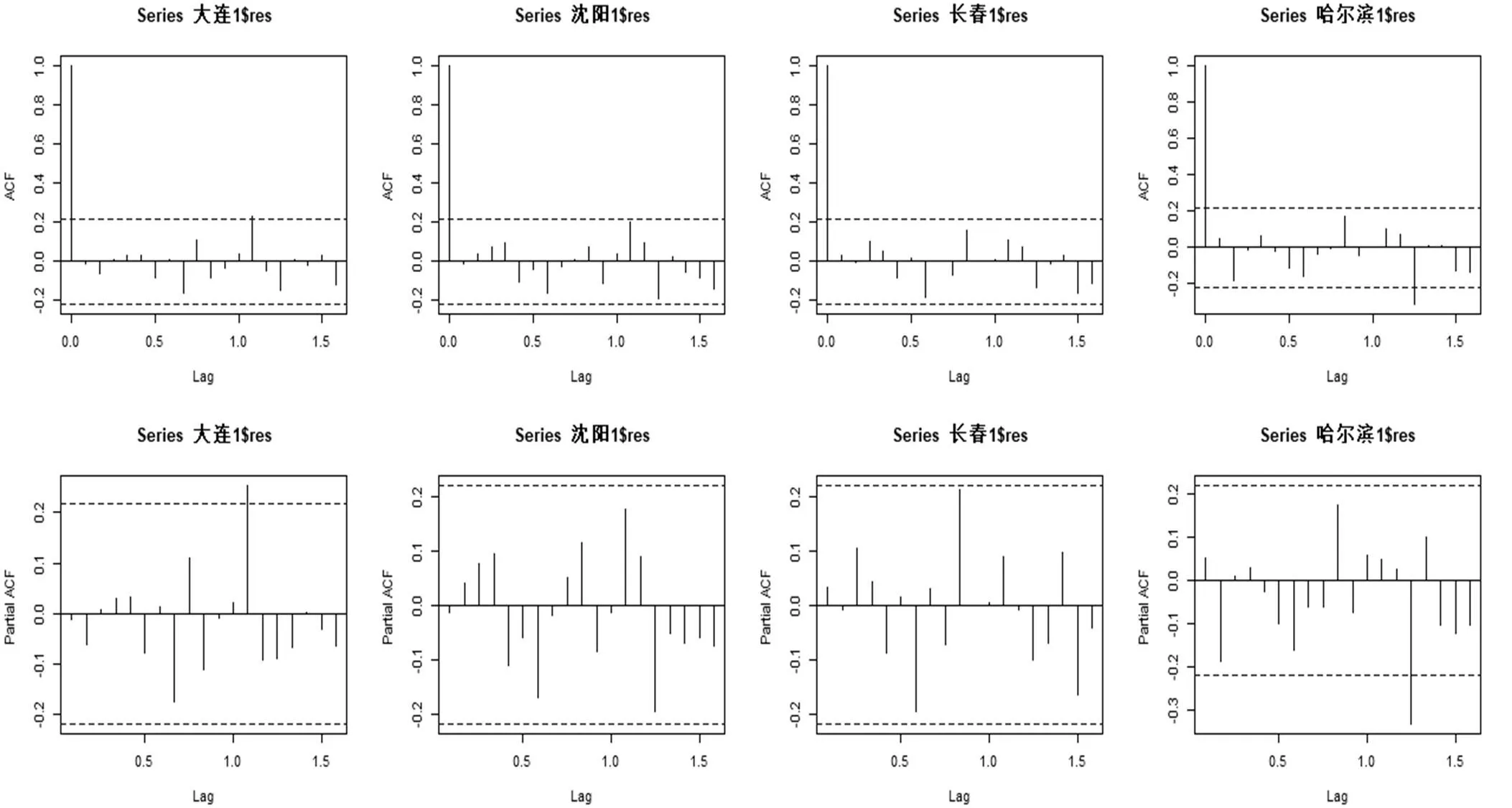
图4 残差相关性图

根据图4各个模型残差序列的相关图显示，残差的自相关系数和偏自相关系数均落在2倍的标准差以内，其无显著相关性，故上述模型均是充分的，且其残差序列为白噪声序列。

4.6 绘制预测图并得出预测数据

4.6.1 绘制预测图

根据四个城市建立的预测模型分别预测未来12个月的AQI指数，得到预测图如图5所示。

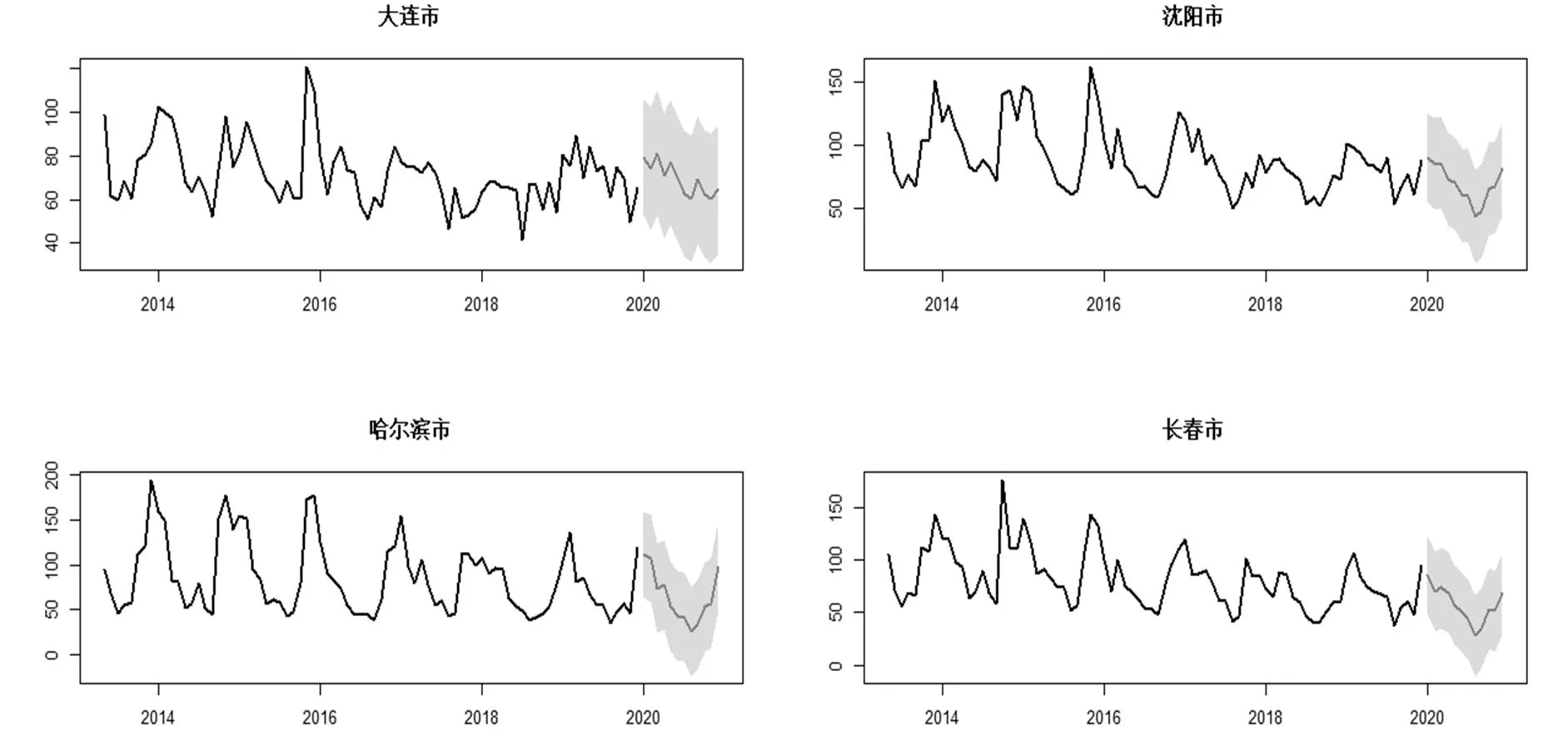
图5 预测趋势图

图5中，沈阳市、哈尔滨市与长春市预测情况相似，各个城市AQI指数大致趋势相同，根据预测图可知，大连市未来一年的AQI指数出现波动，但整体呈下降趋势，其他三个城市仍呈现先减后增的趋势，符合对原有数据探索的规律。总而言之，其AQI指数在未来一年中有所降低。为检验预测模型是否能较好地预测数据，对各个城市的预测数据提取四个月作为参照，将其与真实数据进行对比。

4.6.2 预测数据与真实数据进行比较

根据各个城市预测模型得到的数据与真实数据进行对比得到各个城市的误差表6。

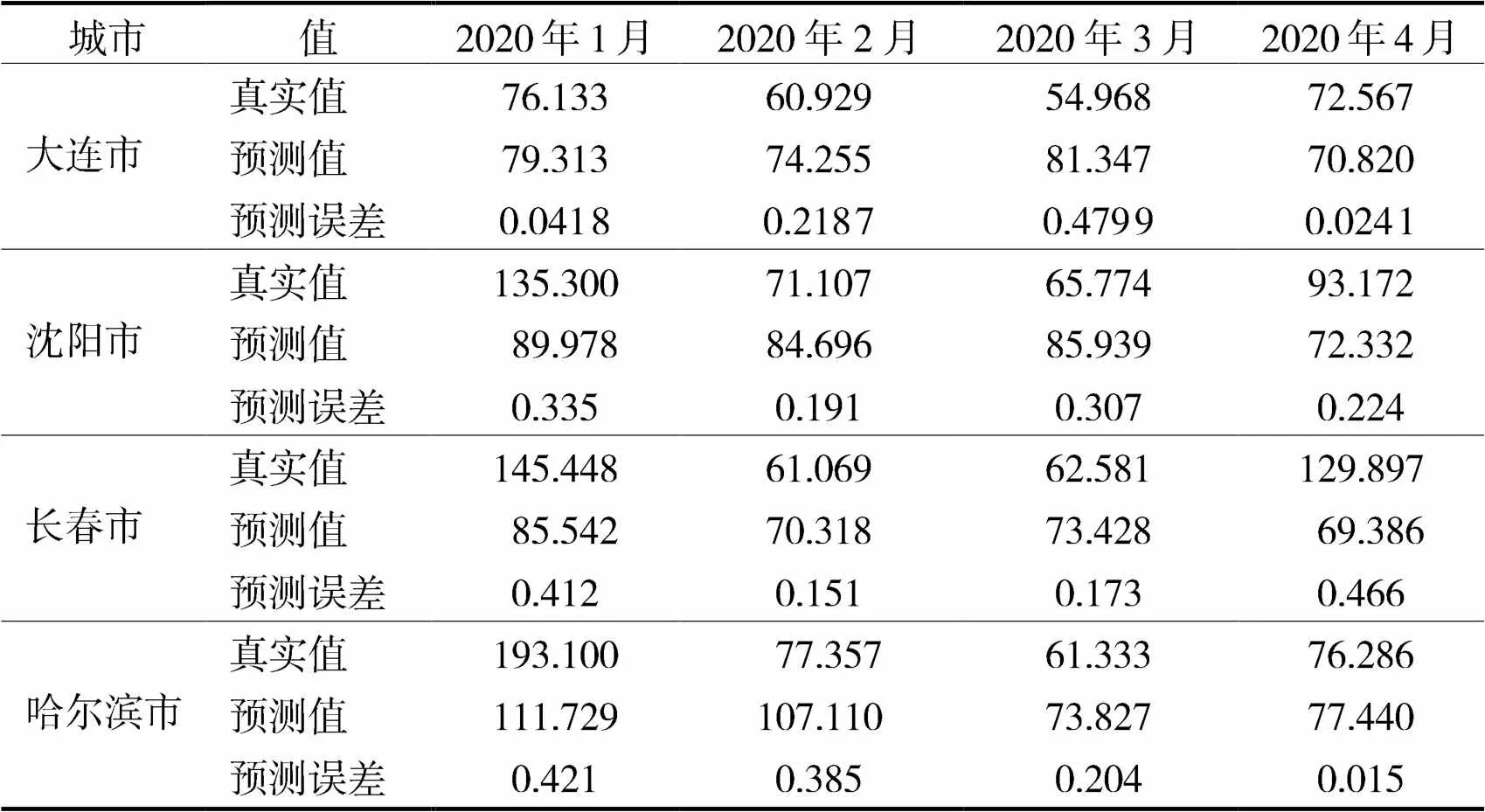
表6 误差表

如上述表所示：上述表为东北四个城市的AQI指数误差表，根据误差表显示，各大城市的预测模型预测效果一般，存在预测误差，但与传统不含季节乘法模型的ARIMA模型相比，其预测效果较优。

5 结论

研究结果表明，在针对含有缺失值的AQI指数数据时，采用缺失森林法填充数据要优于采用均值法填充数据建立的模型，而针对AQI指数的预测模型中ARIMA乘法季节模型优于ARIMA模型。对于东北这四个城市的AQI指数。该四个城市的AQI指数呈现季节变化特征，根据这一变化特征对四大城市分别建立了基于缺失森林填补缺失值数据下的预测模型，预测结果显示各个城市预测效果一般，但与传统不含季节乘法模型的ARIMA模型相比，其预测效果较优。在实际生活中存在一些不可抗因素导致AQI指数的浮动较大，无法做到精准预测，但该模型能比较好地揭示AQI值的发展规律，与未加入季节效应的ARIMA模型相比，效果较为理想。

研究结果显示，在对数据进行随机森林填充后建立的ARIMA季节乘法模型拥有比传统模型较优的预测效果，但仍存在误差，其主要原因如下：

（1）各个城市空气质量变化趋势相似，但具体变化幅度存在差异。根据研究结果表明，针对不同城市，其变化幅度不同，该模型相对而言对变化幅度较小的城市，预测效果较优。

（2）数据受疫情影响较大。本文选取的预测的数据为2020年1月到4月的数据，但2020年初正值疫情爆发时期，突如其来的疫情使得各项生产活动不能如期进行，而选择用疫情之前的数据预测疫情期间的数据，使得预测存在一定误差，现疫情已经得到有效控制，后续会继续收集近期数据进行预测，可以有更高预测精度的预测结果。

[1] 余晓美，沈永昌. 中国环境保护重点城市空气质量的动态特征分析[J]. 统计与决策，2019, 35(11): 91-94.

[2] 孙铭，许梦婷，谢佩锦，等. 基于ARMA模型的哈尔滨市空气质量研究[J]. 哈尔滨师范大学学报（自然科学版），2018, 34(04): 21-25.

[3] 孔朝莉，何文炜. 我国环保重点城市空气质量统计分析和评价[J]. 统计与管理，2020, 35(05): 28-36.

[4] 王雪娇. 黑龙江省不同类型城市空气质量变化特征研究[D]. 哈尔滨：哈尔滨师范大学，2019.

[5] 王未来，李明艳，张美航，等. 我国31个重点城市2014-2018年空气质量变化特征分析[J]. 中国公共卫生管理，2020, 36(04): 441-445.

[6] 严宙宁，牟敬锋，赵星，等. 基于ARIMA模型的深圳市大气PM_(2.5)浓度时间序列预测分析[J]. 现代预防医学，2018, 45(02): 220-223, 242.

[7] 黄珊. 数据驱动模型下的郑州大气污染预测[D]. 郑州：华北水利水电大学，2020.

[8] 肖悦. 中国空气质量时空分布特征及影响因素分析[D]. 重庆：西南大学，2018.

[9] 刘强，裴艳波，张贝贝. R语言与现代统计方法[M]. 北京：清华大学出版社，2016: 299-307.

[10] 李亚伟，刘玲，宋士勋，等. ARIMA乘法季节模型的R软件实现[J]. 环境卫生学杂志，2018, 8(04): 345-349.

[11] 刘佳星，张宏烈，刘艳菊，等. 基于缺失率的不完整数据填补算法[J]. 统计与决策，2021, 37(02): 39-41.

[12] 唐继强，钟鑫伟，刘健，等. 基于时间序列季节分类模型的轨道交通客流短期预测[J/OL]. 重庆交通大学学报（自然科学版）:1-9[2021-04-11].

Air quality prediction based on ARIMA multiplicative seasonal model

TIAN Wen-ting，YU Shi-hang

(College of Science, Qiqihar University, Heilongjiang Qiqihar 161006, China)

In this paper, we use AQI as a standard to evaluate the air quality, and fill in the missing AQI, it is found that the filled AQI has obvious seasonal characteristics, and seasonal features are added to the original Arima model to establish a multiplicative seasonal Arima model. Firstly, four cities in northeast China were selected for empirical analysis, and the missing data were filled in with the mean method and the missing forest method, and then the proper Arima multiplicative seasonal models were established according to their seasonal characteristics, the air quality in the next 12 months is predicted and the future trend is fitted. Finally, the forecast data is compared with the real data, and the Arima model is better than the Arima model in the forecast of air quality, the Arima multiplicative seasonal model with missing forest is better than that with mean value method. All in all, the Arima multiplicative seasonal model based on missing data of missing forest filling is determined to be a better prediction model.

AQI；missing forest；seasonality；arima multiplicative seasonal model

2021-09-11

黑龙江省自然科学基金（LH2019A027）；黑龙江省教育厅科学技术与研究项目（135309477）

田文婷（1998-），女，甘肃定西人，在读硕士，主要从事时间序列应用研究，1549358806@qq.com。

宇世航（1971-），女，黑龙江齐齐哈尔人，教授，博士，主要从事整值时间序列和复杂数据统计推断研究，qqhrysh@163.com。

X831

A

1007-984X(2022)04-0083-07