语音信号频谱的获取

罗海涛

（广东外语外贸大学信息学院，广东 广州 510420）

1 引言

语言是人类特有的能力，是人类信息交流最方便、最快捷的一种方式。[1]信息技术和计算机技术的发展，为人们用计算机处理语音信号提供了方便。通过声音传感器，人们把人类语音转换为连续的语音信号，这是一种电信号。再通过采样技术，对连续的语音信号采样，得到时间和幅度都离散的采样数据。采样数据是离散的数据，便于计算机保存、传输和加工处理。wav文件格式是一种重要的数字音频文件格式，是目前应用很广泛的一种音频格式。相比于其他格式如MP3、MP4、RAM等压缩效率更高的音频文件格式，wav文件没有采用压缩技术，因而其文件要大很多，一般都在几兆字节，甚至更大。[2]本文处理的语音信号采样文件都是wav格式。语音信号的处理包括语音信号的特征分析、语音信号的线性预测分析、语音信号的编码、语音的合成、语音的识别。[3]

语音信号的特征可以应用于语音的基音周期估计、语音共振峰估计、语音识别、说话人识别等领域。语音信号分析包括时域特征分析、频域特征分析。时域特征包括短时能量、短时过零率、短时自相关。时域特征应用于语音的端点检测、语音的分割等。语音信号的频域特征包括语音信号的频谱、相位谱、复倒谱。这些频域特征参数同样可应用于语音的识别、处理、分割等领域。[4]

本文采用快速傅里叶(FFT)算法，计算语音采样数据的频谱和相位谱，为下一步的语音信号处理做准备。

2 语音信号的频谱和相位谱

语音信号的频谱是语音信号在各频率的幅度谱。如果是连续时间信号，则通过傅里叶变换可以得到该信号的频谱，其频谱也是连续的函数。为了用计算机处理语音信号的频谱，只能对语音信号进行采样。采样就是离散化，在时间上离散，在幅度上也离散。离散化后再进行傅里叶变换得到信号的频谱。离散傅里叶变换DFT正是这样一种在时域和频域都离散的变换，其结果是信号的离散的频谱。

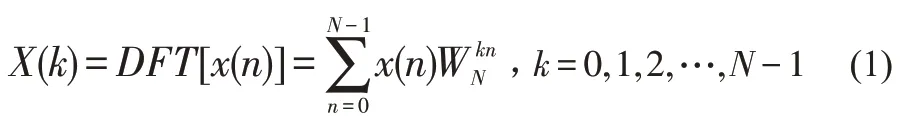
上式中，x(n)是离散化的语音信号，长度为称为旋转因子。该式是N个点的离散傅里叶变换，得到N点的离散频谱[5]。

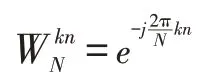
WN是复数，因此由式(1)计算每个X(k)都需要做N次复数乘法和N- 1次复数加法运算，总共需要计算N个点，因此，完成一次DFT变换总共需要N2次复数乘法和N(N- 1)次复数加法运算，运算量非常巨大。特别是在语音信号处理时，其离散点数通常很多，例如，一个英文单词“important”，按照正常语速朗读，当采样频率为44100Hz时，如果没有进行端点检测，采样数据可超过46700；即使通过端点检测，把开始和结束端点以外的采样数据去除，剩余的有效语音采样数据也超过39000。这样大的数据量和运算量，很难进行实时处理，所以通常采用快速傅里叶算法FFT来计算语音信号的频谱。

3 FFT算法

FFT算法分为按时间抽取的基-2算法和按频率抽取的基-2算法两种，这两种算法思路类似，运算量相同。本文采取按时间抽取的基-2算法，在Visual C++环境下编程实现。

按时间抽取的基-2FFT算法的基本原理是在时间域把采样数据平均分为两组，分别是偶数组和奇数组，每组分别进行DFT运算，再合并为最终的结果。而实际做的时候，这两组进一步平均分为4组，4组再进一步平均分为8组，这样一直分下去，直到每一组只有两个采样数据为止。这里有个前提条件是，原始采样数据个数必须是2的幂，即N= 2M，否则需要通过补零的办法，凑够2的幂。

从分解过程可以看出，最后分解到每组只有2个采样数据，这两个数据进行所谓的蝶形运算，生成下一步需要的蝶形运算数据。以8个采样数据的FFT运算为例，其计算路径如图1所示。

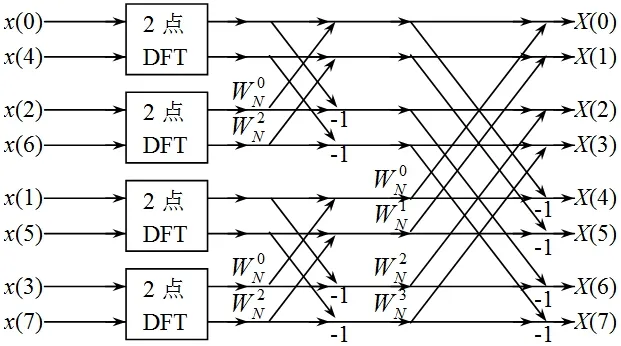
图1 八点采样数据的FFT运算路径

图中，左边输入的是8个采样数据，经过FFT运算，右边得到8个结果数据。其中的两点DFT，以最上面的为例，它的输入x(0)和x(4) ，其上面的输出为：

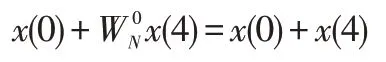
下面的输出为：

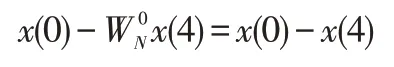
从图中可以看出，输出的运算结果按照十进制顺序X(0)、X(1)、X(2)……X(7) ，但是输入采样数据的次序不是按照x(0)、x(1)、x(2)……x(7)的顺序，而是看上去很“乱”的一个次序。其实把这个输入数据的次序转换为二进制，就可以发现它不仅不“乱”，而且是有规律的。这个规律就是所谓的“倒位序”。

十进制数0到7的二进制数，及其相应的倒位序如表1所示。

表1 0—7的二进制数及其倒位序

实际的采样数据个数往往很多，一般取2的幂，但获得倒位序的方法是相同的。有了倒位序，进行FFT的另一个重要的参数是蝶形运算上下两个节点的间距以及旋转因子WN的变化规律。从图1可以看出来，第1级蝶形运算(图中的2点DFT框)旋转因子只有一个，上下两个节点之间的间距为1。第2级蝶形运算旋转因子有和两个，上下两个节点之间的间距为2。第3级蝶形运算旋转因子有、、和共4个，上下两个节点之间的间距为4。从中可以总结出来规律，设参与运算的采样数据个数总共有N= 2M，则蝶形运算的级数为M级。第M级(最后一级)的旋转因子为、、……以及共M个，上下两个节点之间的间距为N/2 。第M- 1级的旋转因子为第M级的偶数序号的旋转因子，上下两个节点之间的间距为N/4 。依此类推，第1级的旋转因子只有一个，上下两个节点之间的间距为1。

考虑到语音信号的采样数据量很大，一个单词的数据量都接近4万，因此，为了获得语音的频谱，先对语音信号分帧，把采样数据等分为多帧，每帧数据个数相同，这样便于处理。分帧相当于在时域给语音信号施加一个矩形窗。分帧后再计算每一帧数据的FFT变换，这样得到每一帧的频谱。

综上所述，由FFT计算语音信号频谱的运算过程如下：

（1）采样数据分帧，每帧长度相同，帧长取2的整数次方；

（2）根据帧长确定倒位序；

（3）取得第一帧采样数据，加窗，补零使帧长为2的整数次方；

（4）按照倒位序调换该帧采样数据的次序，注意第1个和最后一个采样数据位置不变；

（5）计算帧数据的第1级蝶形，即图(1)中的两点DFT框，旋转因子取为；

（6）由该级蝶形的输入数据，计算该级蝶形输出数据，分别计算实部和虚部；

（7）蝶形的级数加1；

（8）判断级数是否等于M，若等于M，转第(10)步；

（9）计算本级蝶形的旋转因子，转第(6)步；

（10）数据帧序号加1；

（11）判断帧序号是否达到最大，若是，表明所有帧数据处理完毕，结束；

（12）转第(3)步。

上述运算过程完成了一个语音文件的所有帧的FFT运算，得到了每一帧数据的频谱。

4 运算结果

本文在VC++环境下，编程对英文单词进行分帧以及FFT变换，得到相应的帧频谱和相位谱。

第一个对单词“dictionary”的音频文件进行处理，首先进行端点检测，去除起始端点和结束端点之外的采样数据，以减少需要处理的数据量。再分帧并进行FFT变换，以获得每帧的频谱和相位谱，分帧结果如下：

Total # of samples: 33547

Bits per sample: 16

Sample Rate: 44100

Frame length: 20.58(ms).= 907(points)

Frame shift: 0.7529 = 682(points)

Total # of frames: 49

Last frame, # of speech data (iNLast=): 811(points)

data window style: Rectangle(default) iWinStyl= 1

Frame length for FFT : 1024 = 2 ^ 10

分帧后画出语音波形、选中第一帧并画出该帧语音波形，再进行FFT变换得到频谱及相位谱如图2所示。

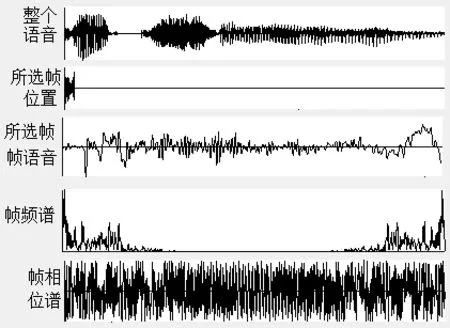
图2 “dictionary”语音及其第1帧波形及频谱和相位谱

第2帧运算结果如图3所示。

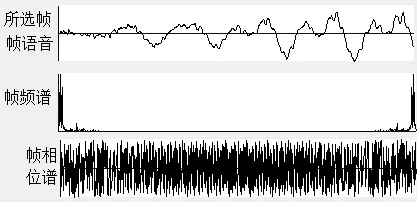
图3 “dictionary”第2帧波形及频谱和相位谱

第30帧运算结果如图4所示。

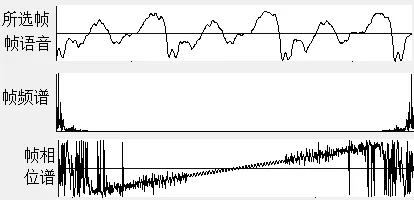
图4 “dictionary”第30帧波形及频谱和相位谱

其他语音音频文件的运算结果不再一一列举。

5 结语

计算机处理语音信号，必须采用时域和频域都离散的形式。而语音信号离散化后，实际上就是一些采样数据，其处理方式需要采用数字信号处理技术。时域处理可以获得信号的时域特征，例如帧能量、帧过零率等等。而频域处理获得频域参数，例如频谱、相位谱，这些频域参数可以用在语音信号数字滤波器的设计、语音语谱图的形成等领域。