气-液横向流动下悬臂柱体结构涡激振动机理研究*

严 浩，代胡亮，王 琳，倪 樵

（1.华中科技大学 航空航天学院 工程力学系，武汉 430074；2.工程结构分析与安全评定湖北省重点实验室，武汉 430074）

引言

涡激振动是工程实际和日常生活中一种常见的流致振动现象，其主要原理是：流体以一定的流速流经钝体(如圆柱体)时，会在结构后方两侧产生周期性漩涡脱落现象，进而产生作用于结构之上的周期性流体力，从而导致结构振动.尤其当旋涡脱落频率接近结构的固有频率时，“锁频(lock-in)”现象[1]出现，导致结构发生大振幅的共振运动.而这种共振恰恰是诱发诸如热交换器、桥梁、海洋立管和海底管线等工程结构发生疲劳损伤和破坏以及工质泄漏的主要原因之一.因此，涡激振动问题成为当前学术界和工业界关注和研究的重点.

早期的研究主要集中在刚性圆柱体的涡激振动问题上，且已取得了大量的研究成果.近几十年来，细长弹性结构的涡激振动问题吸引了大量学者们的关注和研究，其研究途径主要为实验研究[2]、数值模拟[3]和经验模型[4]等.相较于前两种方法，经验模型具有成本低、效率高、预测效果较好的优势.因此，经验模型得到了许多学者的青睐，其中尾流振子模型是应用较为广泛的经验模型之一.

1964年，Bishop 和Hassan[5]认为尾流对于圆柱体的作用相当于一个非线性振子，于是提出了尾流振子模型来研究圆柱体的涡激振动问题.随后，Griffin 等[6]结合实验和理论，验证了他们所提出的新改进尾流振子模型，并发现圆柱体在锁频区内的位移和升力之间的相位角可能发生突变.1975年，Skop 和Griffin[7]在研究弹性圆柱体的涡激振动问题时，将应用于刚性圆柱体的涡激振动模型改进为适用于弹性圆柱体的模型.进入20世纪90年代后，Skop 和Balasubramanian[8]发展了Skop 和Griffin[7]此前所提出的模型，并将新模型成功应用到细长弹性圆柱体的涡激振动研究中，这种新模型能够在无阻尼条件下保证圆柱体响应的渐近性和自控性.2004年，Facchinetti 等[9]分别研究了基于位移耦合、速度耦合和加速度耦合的尾流振子模型来研究结构的涡激振动行为.通过实验和理论的对比分析，结果表明加速度耦合更能准确地预测结构的涡激振动响应.此后，Violette 等[10]利用Facchinetti 等[9]提出的加速度耦合模型，研究了受均匀流和剪切流作用下细长弹性圆柱体的涡激振动问题，所得预测结果通过了数值模拟和实验的验证.目前，尾流振子模型已被广泛应用于水和空气中圆柱体的涡激振动研究，且被证明对于均匀和非均匀流都能得到一定的应用.

当潜艇在水下航行进行侦查时，其望远镜将举升出水面.此时，望远镜的下部和上部将分别受到水流和气流的作用，且在一定情况下将发生涡激振动现象，这将严重影响观测精度.受此启发，本文基于尾流振子模型，建立了悬臂柱体结构受气-液两种不同横流作用下的涡激振动理论模型，并研究了这两种横流分布比和密度比等参数对结构涡激振动响应的影响.

1 理论建模

考虑如图1所示的悬臂圆柱体，其沿x轴的长度为L，截面外直径为D，内径为Di，密度为 ρc，抗弯刚度为EI.该圆柱体在气-液两种横流的作用下发生涡激振动.其中，气-液两种横流分别分布于圆柱体结构的上下两部分，它们之间的分界线位于x=L1处.此外，液体横流的流速和密度分别为U1和 ρ1；气体横流的流速和密度分别为U2和 ρ2.为了便于研究，本文做出如下假设：1）圆柱体为细长、等截面结构，采用Euler-Bernoulli 梁建模；2）仅考虑圆柱体y方向上的振动；3）忽略圆柱体结构的重力、浮力、剪切、扭转和Poisson 比的影响；4）考虑圆柱体为黏弹性材料(Kelvin-Voigt 型)，E∗为黏弹性系数.

图1 气-液横流作用下的悬臂圆柱体涡激振动模型示意图Fig.1 The vortex-induced vibration model for a cantilever cylinder under gas-liquid cross flow

基于上述假设，悬臂圆柱体在气-液两种横流作用下的非线性涡激振动控制方程可以通过Hamilton 原理推导得到[11]，其具体形式如下：

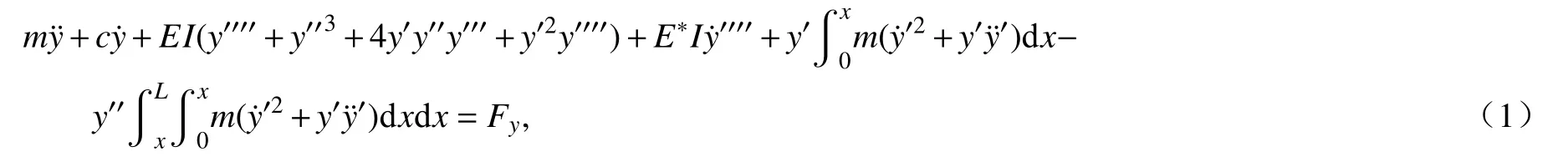
其中y(x,t)表示圆柱体的横向振动位移，x和t分别表示柱体轴线坐标变量和时间变量，上标符号“·”和“′”分别表示变量对t和x的偏导数.

2 求解方法

3 结果与分析

理论上讲，Galerkin 截断数N越大，数值结果越收敛，越接近精确解.因此，我们首先需要确定一个合适的Galerkin 截断数N，以便高效地得到可靠的数值结果.截断数N的收敛性分析如图2所示.图2(a)给出了圆柱体仅受折合流速为5 的单一外流(水)作用时的自由端振动响应，可以看出，N=5,6,7,8,9 的结果基本一致.图2(b)给出了圆柱体受折合流速均为5 的两种外流(空气、水)作用的自由端振动响应，可以看出，N=5,6,7 的结果与N=8，9 的结果有明显差异.结合图2(a)和2(b)，基于数值计算的可靠性和计算效率，选取N=9.

图2 不同模态截断数N 下的圆柱体自由端振幅：(a)仅有水作用的情况，Ur1=5；(b)空气和水共同作用的情况，Ur1=Ur2=5Fig.2 Amplitudes at the cylinder’s free end for different Galerkin truncation number N values:(a)only water case,Ur1=5;(b)air-water case,Ur1=Ur2=5

为了研究圆柱体在气-液两种横流作用下的涡激振动响应，图3 给出了圆柱体自由端振幅ymax/D随折合流速Ur1和Ur2变化的云图.可以看出，圆柱体振幅在Ur1≈5区域内的值明显高于其他区域，且振幅的最大值出现在Ur1=Ur2=5处.这说明，在空气和水两种横流共同作用下，圆柱体的涡激振动响应主要受水流的影响，而空气的影响甚微.这种现象的主要原因在于水的密度远大于空气的密度，黏附于圆柱体表面的附加水质量远大于附加空气质量，进而导致与水相关的流体力远大于空气的.

图3 圆柱体自由端振幅随折合流速U r1和U r2变化的云图Fig.3 The contour of amplitudes at the free end of the cylinder，as a function of reduced velocities U r1 and Ur2

考虑到Ur2对圆柱体振动响应的影响较小，在后续的数值计算中默认Ur1=Ur2.接下来，本文将详细讨论流体分布比χ 和密度比κ 以及黏弹性系数α对圆柱体振动响应的影响.

流体分布比χ 对圆柱体在锁频区内振动响应的影响如图4所示.根据该图可知，随着χ 的增大，圆柱体的锁频区域逐渐扩大，振幅的最大值先增大后减小，且在χ=0.5，Ur1=Ur2=5.1处出现极大值.当χ 逐渐减小至0.1 时，自由端振幅随折合流速的变化逐渐趋同于仅有空气横流的情况.这是因为χ 趋近于0 时，系统将退化为只有空气外流作用下的涡激振动模型.当χ 逐渐增大至0.9 时，自由端振幅随折合流速的变化逐渐趋同于仅有水流的情况，因为χ=1 时，系统退化为仅有水流作用的涡激振动模型.这种可以退化的现象反映出本文所建立的两种流体作用下圆柱体的涡激振动模型的合理性和正确性.

图4 不同分布比时，圆柱体自由端振幅随外流折合速度的变化曲线Fig.4 The relationship between the amplitude at the free end of the cylinder and the reduced velocities of external fluids with different fluid distribution ratios

由上述分析可以看出，圆柱体在Ur1=Ur2=5附近振幅达到最大值.在下面的数值分析中，为了更准确地探究其他参数对圆柱体振动响应的影响，均选取Ur1=Ur2=5为例进行计算.

由图5 可知，圆柱体自由端振幅受到分布比χ 和密度比 κ 的共同作用.当χ≤0.3时，振幅随着κ的增大而增大；当χ≥0.4时，振幅随着κ的增大而减小.当κ不断减小时，振幅随分布比χ 变化的曲线逐渐与空气-水的结果重合，且曲线峰值不断增大；当κ不断增大时，曲线逐渐拉直趋于水平，且曲线峰值逐渐减小.这说明振幅的最大值与κ之间呈反比例变化.此外，圆柱体自由端振幅随着分布比χ 的增大先增大后减小，该现象与图4 中的结果吻合.

图5 Ur1=Ur2=5 时，不同密度比作用下圆柱体自由端振幅随流体分布比的变化曲线Fig.5 The relationship between the amplitude at the free end of the cylinder and the fluid distribution ratios with different fluid density ratios,Ur1=Ur2=5

黏弹性系数 α对圆柱体振动响应的影响如图6所示.可以发现，不论分布比χ 为何值时，圆柱体自由端振幅随着黏弹性系数α的增大均不断减小.这说明分布比χ 和黏弹性系数α之间的耦合作用并不明显.

图6 Ur1=Ur2=5 时，不同黏弹性参数作用下圆柱体自由端振幅随流体分布比的变化曲线Fig.6 The relationship between the amplitude at the free end of the cylinder and the fluid distribution ratios with different viscoelastic coefficients,Ur1=Ur2=5

为了探究气-液两种横流作用下圆柱体涡激振动的具体运动形式，图7 和图8 分别给出了不同分布比χ 作用下圆柱体自由端振动响应的相图和功率谱密度图.由图7 可知，当χ 为0.3 和0.6 时，圆柱体的相图均为标准极限环；当χ 为0.9 和1 时，圆柱体的相图均为有限数目的圆环.分布比χ 分别为0.3 和0.9 时，圆柱体振动响应的功率谱密度曲线如图8(a)和(b)所示，可以发现，两条曲线均十分光滑.但是，χ=0.3 时的曲线仅含一个主峰，χ=0.9 时的曲线有多个峰值.结合图7 和图8 可知，当分布比χ 接近1 时，圆柱体做多周期运动，当分布比远离1 时，圆柱体做单周期运动.

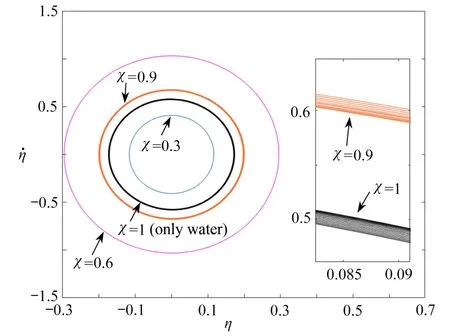
图7 Ur1=Ur2=5 时，不同流体分布比作用下的相图Fig.7 The phase portrait with different fluid distribution ratios,Ur1=Ur2=5

图8 Ur1=Ur2=5 时，不同流体分布比作用下的功率谱密度图Fig.8 The power-spectrum-density diagrams with different fluid distribution ratios,Ur1=Ur2=5

4 结论

本文构建了悬臂柱体结构受气-液两种不同横流作用下涡激振动的理论模型.基于Galerkin 法和Runge-Kutta 法进行了数值求解，研究了柱体结构在气-液两种横流作用下的涡激振动机理和规律.研究表明，圆柱体的涡激振动响应主要受到液流的影响，其主要原因为液流的密度远大于气流.当流体分布比越大，即液流占比越大时，圆柱体的涡激振动锁频区越大.但是，圆柱体在锁频区内的最大振幅随着分布比的增大呈现先增大后减小的趋势，且峰值出现在分布比约为0.5 附近.此外，该峰值随着流体密度比的减小呈现明显的增大趋势.这说明，当两种横流间的密度相差越大，其可能出现的振幅极值也越大.因此，为防止柱体结构出现过大幅度的振动，应避免两种横流均等分布的情况.当分布比较小时，柱体结构做单周期运动，而当分布比接近1 时，柱体结构做多周期运动.本文的研究成果对潜艇侦查望远镜结构的设计、分析与使用具有一定的理论指导意义.