主动冷却点阵夹层防热结构温度响应计算模型*

彭世彬，郭 瑞，冯上升，金 峰

（1.西安交通大学 机械结构强度与振动国家重点实验室，西安 710049；2.西安交通大学 仿生工程与生物力学研究所，西安 710049；3.西安交通大学 生物医学信息工程教育部重点实验室，西安 710049）

引言

点阵夹层结构由于同时具备承受机械载荷和热载荷的双重功能而在航空航天领域具有广阔的应用前景[1-3]，如超高音速飞行器的热防护部件[4]，火箭发动机的燃烧室[5]，以及航空母舰上的偏流板[6]等.现有关于点阵夹层结构热学特性的研究主要集中在稳态传热，然而在上述应用中，结构表面的热载荷通常是随时间急剧变化的，因此，探究点阵夹层结构在非稳态热载荷作用下的温度响应十分必要.

相比于孔结构随机排列的开孔金属泡沫，具有周期性单胞的点阵夹层结构在力学载荷作用下芯体变形以杆件拉伸为主导，因此在相同的孔隙率下具有更优异的比强度/刚度[7].在传热方面，点阵结构既增加了散热面积，又可在芯体通道内产生流动漩涡并促进流体扰动，从而增大表面对流换热系数；而且其内部流动更加有序，比随机开孔金属泡沫具有更低的压降[7].因此，点阵夹层结构在承载-散热多功能应用场合更具综合优势.Kim 等发现四面体夹芯板的散热效率是空通道的6 倍左右[8].Lu 等利用PIV 粒子成像技术揭示了四面体点阵夹芯板中的流场分布，证明夹芯杆与面板之间形成的涡流是引起传热强化的主要原因[9].Yan 等通过冲压金属薄板制作了一种轻质X 型点阵结构并研究了其对流换热性能，研究发现X 型点阵独特的结构形态导致大规模的螺旋主流，它与二次流相互作用提高了换热能力[10-11].截至到目前，大部分研究集中在对点阵结构内部流动换热机理的探究方面，而对其在非稳态热载荷作用下的温度响应鲜有研究.此外，在理论模拟方面，过去的研究主要针对均匀热边界条件，采用CFD 数值方法模拟一个或者一排单胞内的流动传热[12]，然而对于工程中的非均匀热边界条件问题，需要的计算区域更大，计算非常耗时.现有理论建模一般是基于翅片理论，将点阵夹芯杆中的热传导简化为表面对流的一维翅片导热[8]，翅片根部的温度认为等于连接面板表面的平均温度；实际上，由于芯体杆件根部的面积较小，热量在透过面板的过程中逐渐向杆件根部聚集，导致杆件根部的温度要低于连接面板表面的单元平均温度，而现有的研究都忽略了这一重要影响因素.

综上，本文以金字塔点阵结构为研究对象，研究了主动冷却下承受非稳态热载荷的点阵夹层结构及内部流体的温度响应问题，建立了夹层结构导热与冷却剂对流耦合的理论模型，利用分离变量法推导了夹芯杆根部与连接面板之间收缩热阻的近似解析解，并开展数值模拟验证了理论模型.

1 理论模型

1.1 模型介绍

图1 为本文研究的金字塔型点阵金属夹芯结构的对流换热示意图.考虑该金字塔型点阵夹芯结构在主动冷却作用下承受非稳态热流密度时的温度响应问题.外界热量由上面板输入，下面板底部处于绝热状态，冷却液以初始温度Tcool= 300 K 流入夹芯板带走热量.上、下面板厚度为tb= 0.8 mm，夹芯高度为H= 5 mm，夹芯杆直径为d= 1 mm，夹芯杆与下面板的夹角为θ = 45°.

1.2 非稳态传热控制方程

1.3 控制方程离散化

1.3.1 结构体控制方程离散化

针对点阵结构周期排列的特点，以流动方向上每个单胞的上、下面板为面板离散的最小单元，以单胞内流体区域为流体域的最小离散单元，每个单胞内的夹芯杆沿着长度方向进行区域离散，点阵夹层结构及内部流体的离散示意图如图2所示.

图2 点阵夹层结构及内部流体的离散示意图Fig.2 Discretization of the lattice sandwich structure with internal fluid

1.3.2 流体控制方程离散化

在MATLAB 中对结构和流体的非稳态传热代数方程进行迭代求解，具体的过程如下：

1)选取合适的时间步长Δt和空间步长Δη；

2)为结构域和流体域赋予初始温度(300 K)；

3)计算下一时刻上、下面板和夹芯杆及流体域离散方程中的附加热源项；

4)计算下一时刻结构域和流体域中离散单元内的温度；

5)将下一时刻结构域和流体域的温度作为初始温度，重复步骤3)～5)，直至整个非稳态过程结束.

计算在满足收敛条件的情况下，取Δt= 0.004 s，Δη = 0.35 mm 足够满足计算精度.

1.4 确定对流换热系数

上述离散后的代数方程中出现的两个对流换热系数hb和hfin是未知的，因此理论模型并不完整.为此，采取基于单胞的周期性流动传热模型进行仿真求解，具体做法如下.

7）如果 len（Lborder[]）＞len（Rborder[]），就把 w-1加入到右边界列表中（防止没有检测到最后一个字符的右边界）。进入步骤8）。

首先根据结构对称性建立只有半个单胞的周期性流动传热模型.将流体进出口设置为周期性边界条件，流体进口的平均速度在u0= 0.2～1.0 m/s 范围内变化，固体域及流体域左右侧均设置为对称边界，流固交界面设为无滑移耦合传热边界条件，单胞上面板给定恒定的热流密度128500 W/m2，其他壁面设置为绝热边界.在Fluent Meshing 中对当前模型进行网格划分，网格类型采用多面体型，对壁面边界层处进行加密处理确保y+<1，湍流模型选用k-ω SST，该模型在计算复杂分离流时具有优越性，能够很好地预测剪切流动中的流动分离现象[14]，因此非常适用于当前流动模型中漩涡流的模拟.采用SIMPLE 算法耦合压力和速度进行数值分析，对流项的离散采用二阶迎风格式，动量方程的迭代收敛准则为10−3，能量方程的迭代收敛准则为10−7.图3中展示了模型的计算域、边界条件和网格.

图3 周期性流动传热数值模拟：(a)计算域及边界条件；(b)网格Fig.3 Numerical simulation of periodic flow and heat transfer:(a)the computational domain and boundary conditions;(b)the mesh

定义Red，hb和hfin为[9]

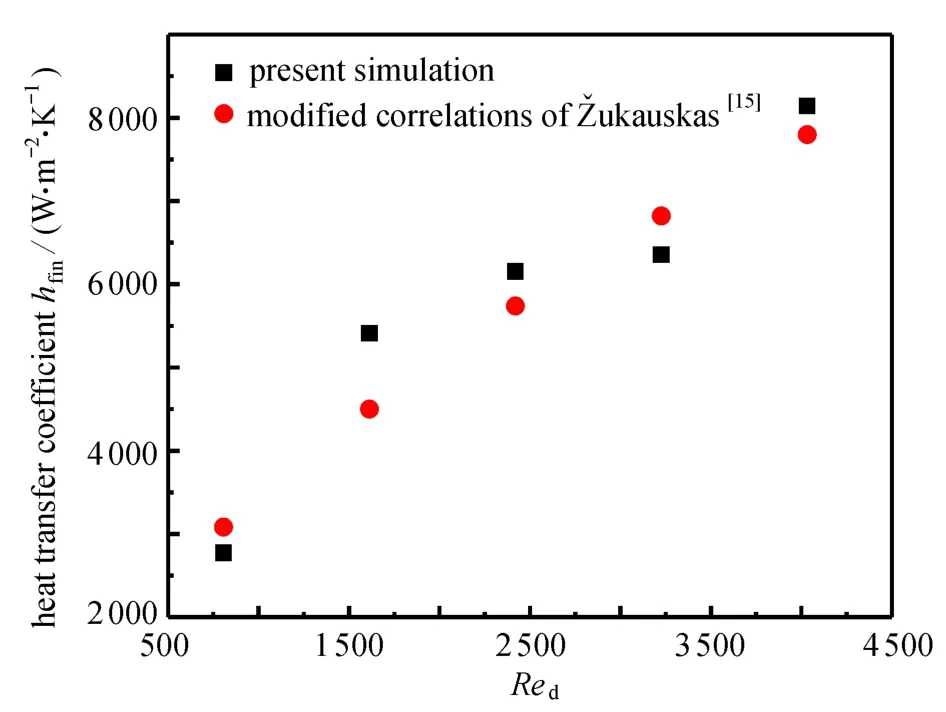
图4 不同Red 下，夹芯杆表面的对流换热系数Fig.4 Heat transfer coefficients on the surface of lattice struts under different Red values

1.5 求解收缩热阻

面板-点阵之间的收缩热阻的求解可以等效为以下问题：如图5所示，一块矩形板顶部承受均匀热流，四周绝热，底部分别受到不同程度的对流冷却作用，即在面板内表面的中间与翅片连接界面上的等效对流换热系数为heff，而其他直接接触冷却流体区域的表面对流换热系数为hb.由于模型的对称性，可取图5 中模型的1/4 进行求解，因此该问题的控制方程和边界条件可表示为

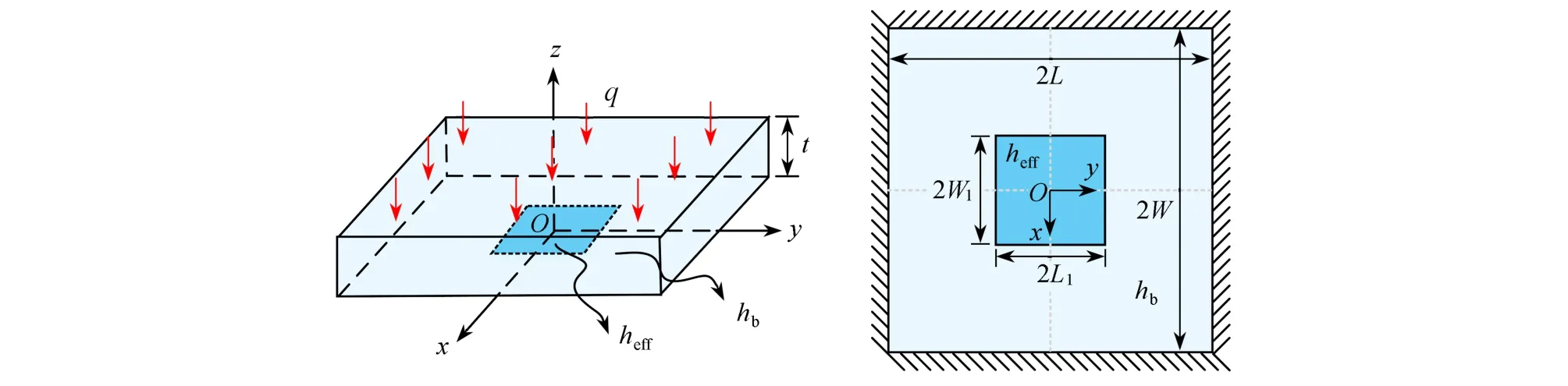
图5 求解收缩热阻的等效模型Fig.5 The equivalent model for solving the constriction thermal resistance

对于一般的情况，由于方程的复杂性，可在MATLAB 中进行迭代求解，具体过程如下：

1)选择所需的扩展项数量(N×N)；

2)令cmn=dmn= 0(下表面均匀换热)作为初始值；

3)将dmn代入式(45)和(47)计算新的A，B和cmn；

4)将cmn代入式(46)得到新的dmn；

经过验证，N= 30 足够满足求解精度，并设置两次迭代之间dmn的变化小于0.001.

2 数值模型

为验证当前理论模型的准确性，对所示的点阵结构进行数值模拟，考虑到计算资源的限制，沿流动方向的单胞数量取n= 10，但对理论计算模型n可以远大于10.结构材料设为钢，其密度ρs= 8 030 kg/m3，热导率ks=16.27 W/(m·K)，定压比热容cps= 502.48 J/(kg·K).冷却剂为航空煤油JP-7[18]，密度ρf= 800 kg/m3，定压比热容cpf= 2575 J/(kg·K)，热导率kf= 0.11 W/(m·K)，黏度µf= 1.984 × 10−4kg/(m·s).

图6 展示了模型的计算域及边界条件：本文中首先按照1.4 小节中的方法对单胞进行周期性流动传热模拟，为避免入口效应，入口边界上的速度直接读取周期性流动传热模拟得到的周期边界上的速度分布，出口采用压力边界，上面板外表面采用非稳态热流边界，时间步长设置为1 s，两侧为对称边界，流固交界面采用无滑移耦合传热边界条件，其余面均为绝热边界.网格类型、划分方式及湍流模型均与单胞周期性模拟一致.为确保计算结果与网格数量无关，取加热表面平均温度为监测值进行网格独立性验证，测试网格数从120 万增加到400 万，发现在网格数量超过340 万时计算结果已无明显变化，如图7所示，因此最终采取的网格数为340 万.

图6 含多个单胞点阵夹层结构数值模拟计算域及边界条件Fig.6 The numerical simulation domain and boundary conditions for the multi-cell lattice sandwich structure

图7 加热面平均温度随网格数量的变化曲线Fig.7 The variation of the average temperature of heating surface with the number of meshes

3 结果与讨论

3.1 理论与仿真对比

本文算例中采用可重复使用运载器(RLV)进入大气时表面产生的瞬时热通量作为外加热源，以确定理论模型的适用性.RLV 表面的气动加热曲线如图8所示，瞬时热通量从0 s 变化到2200 s，其中qmax= 128500 W/m2是热通量的最大强度，2200 s 是再入过程的最后时间.RLV 表面的热通量分布假定为分段多项式，各阶段具体的表达式见文献[19]中的表1.

图8 RLV 再入过程中表面的入射热通量随时间的变化曲线Fig.8 The incident heat flux profile vs.the re-entry time on the RLV surface

将整个点阵结构的最大温度Ts,max(沿流动方向最后一个单胞的上面板外表面平均温度)以及流体出口的温度Tf,out作为考核目标并进行理论与仿真结果对比.图9(a)为不同流体平均进口速度(u0= 0.2～1.0 m/s)下点阵结构的最大温度随时间的变化曲线，从图中可以看出，理论结果与CFD 仿真结果吻合良好，最大误差低于1%.图9(b)为流体出口温度随时间的变化曲线，在当前的验证模型中，由于总尺寸较小，同时冷却剂流速较大，导致与入口温度相比，出口温度并无明显上升，但在整个非稳态过程中理论结果与CFD 结果高度吻合.

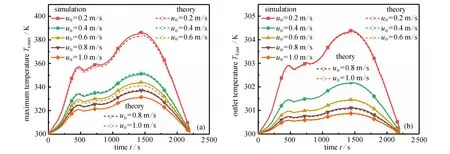
图9 结构最大温度与流体出口温度的变化曲线：(a)结构最大温度；(b)流体出口温度Fig.9 Variations of the maximum temperature of the sandwich structure and the outlet fluid temperature with time:(a)the maximum temperature of the sandwich structure;(b)the outlet fluid temperature

3.2 收缩热阻对模型精度的影响

图10 给出了u0= 0.2 m/s 时，不同的恒定热流密度下点阵结构所能达到的最大温度，从图中可以看出，忽略收缩热阻使得计算结果偏低，并且随着热流密度不断增大，忽略收缩热阻使得计算结果造成的误差呈放大趋势，因此在外界热载荷较高时不能忽略收缩热阻的影响.

图10 不同热流密度下结构的最大温度Fig.10 The maximum temperature of the structure under different heat flux densities

3.3 导热率和面板厚度对收缩热阻的影响

图11 和12 分别给出了在不同流体进口速度下收缩热阻随导热率和面板厚度的变化曲线.结果表明，在不同的流速下，收缩热阻随着导热率以及面板厚度的减小而增大，并且随着流速增大而减小，因此在冷却剂流速比较小时，忽略收缩热阻会造成较大的误差.

图11 不同流体进口速度下收缩热阻随导热率的变化曲线Fig.11 Variations of the constriction thermal resistance with the thermal conductivity under different inlet fluid velocities

图12 不同流体进口速度下收缩热阻随面板厚度的变化曲线Fig.12 Variations of the constriction thermal resistance with the facesheet thickness under different inlet fluid velocities

4 结论

本文建立了可用于非均匀、非稳态复杂热载荷下快速预测点阵夹层结构温度响应的非稳态传热理论模型，首次考虑了夹芯杆根部与连接面板之间收缩热阻对点阵夹层结构传热的影响，并用数值方法进行了验证.得到的结论如下：

1)理论模型能够准确预测金字塔点阵结构以及内部流体的温度场变化，理论结果与模拟结果吻合良好，最大误差不超过1%，在考核算例下计算耗时仅为CFD 模拟的4%.

2)随着外加热流密度不断增大，忽略收缩热阻使得计算结果造成的误差不断增大.

3)收缩热阻随着导热率以及面板厚度的减小而增大，随着冷却流体进口流速增大而减小.因此，在高热流密度、薄面板厚度以及低冷却剂流速条件下预测点阵夹层结构传热特性，必须考虑面板与点阵芯体之间的收缩热阻.