基于多因素不确定环境的受扰航班恢复建模与仿真*

□ 田倩南,张成勇,李 杰,冷凯君

(1.湖北经济学院 湖北物流发展研究中心，湖北 武汉 430205；2.华中科技大学 管理学院,湖北 武汉 430074)

据国际航空运输协会(International Air Transport Association,IATA)的数据，2019年全球航空业的旅客总量为45.8亿人次，比2018年增长6%。其中，2019年中国民航旅客运输量6.6亿人次，同比增长7.9%。民航进一步与综合交通深度融合，其旅客周转量在综合交通运输体系中占比达32.8%，同比提升1.5%，与其他运输行业相比，航空运输具有速度快、效率高、覆盖范围广等多种优势，与此同时，也容易因天气(大规模台风和雨雪雾等)、航空公司(机组人员空勤或航班计划调整等)、空管(流量控制等)及其他因素(旅客等)(如表1所示)而产生延误。比如，2018年我国主要航空公司(全年航班量排名前十的航司)平均航班正常率只有75.62%。据估算，我国民航业由于各种因素导致的延误带来的总经济损失每年不少于500亿元人民币。

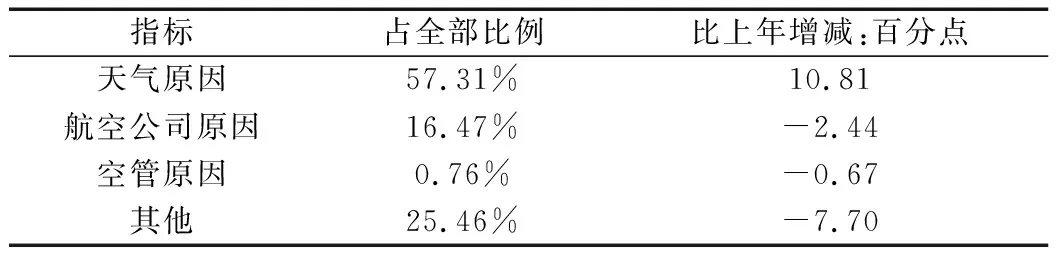
表1 2020年航班不正常原因分类统计

受扰航班恢复问题是指当原来的航班计划遇到干扰(如飞机故障等因素)使得部分航班延误甚至取消，出现原航班计划不可行的情况，这就需要对原来的航班计划进行重新排列以快速恢复飞机航线(航线是由航班组成的)，降低航空公司的损失。当航班发生延误时，航空公司运行调度人员需要对航班计划进行实时调整，使航班在最短时间内恢复正常，同时还要确保公司为此支付的成本最小。其中，航班计划是航空公司在整个航线网络上对所有航班进行设计和优化的过程，完整的航班计划包含航线、航班(航班号、起降时刻、起降机场等信息)、班期(某航班在周期内的哪几天被执行)、班次(每个航线上有多少航班)、机型(飞机型号)等信息，它是航空公司运营活动的基础，也是航空公司整个运营计划的核心，飞机排班、机组人员排班等都是在此基础上展开的。因此，研究受扰航班恢复问题有着重要的现实意义，不仅能够提高航空公司的运营效率，还可增强调度方案的灵活性，也为接下来机组排班计划的研究提供科学依据。

从上个世纪六十年代开始就有关于航空公司受扰航班恢复问题的论述。Jedlinsky[1]提出了一个最小费用流模型来对该问题进行建模，建立实时信息系统，采用网络流理论中的out-of-kilter算法对问题进行求解。Gershkoff[2]采用时空网络方法求解受扰航班恢复问题，但在该研究中没有考虑实际生活中出现的情况，如允许航班延误、允许航班交换等，从而缺乏可行性。Teodorovic和Stojkovic[3]对已有的模型进行改进，将目标函数分为两阶段：在第一阶段中要求最小化航班取消的总数量，在第二阶段中要求最小化旅客的总延误时间。该文是第一个提出同时考虑恢复航班时刻和飞机路线的，并且还考虑了机场宵禁约束的要求，遗憾的是文中并没有给出具体算例的测试。Bierlaire等[4]以最小恢复成本为目标函数，采用列生成算法对该问题进行求解，但是在子问题的求解过程中，只考虑了取消航班和延误航班，这样就会导致大量的航班被取消或者航班延误时间过长，因此给旅客带来极大的不便。白凤等[5]研究了因飞机资源短缺和机场关闭造成的航班不正常情况，不足的是该文献没有考虑飞机维修的情况。Bisaillon等[6]将航班恢复与乘客重新安排一起考虑，采用宽领域搜索算法，其枚举式的搜索效率比较低，解决问题规模小。Hu等[7]是以飞机延误成本和旅客退票重新分配成本之间费用的平衡为目标，在算法GRASP基础上进行求解的。乐美龙等[8]以最小化乘客总延迟时间为目标，用计算机软件进行求解。杨欢等[9]研究了基于动态环境的机场航班实时调度优化的初级阶段，采用遗传算法求解优化模型。陈茂林等[10]对民航调度系统中的空管、机场和航空公司之间复杂的协同调度问题进行研究。Sinclair等[11]对航班恢复和旅客恢复进行了综合研究，采用启发式算法进行求解，增加了问题的求解规模，但是在恢复措施中，航班推迟采取的是分段推迟，而不是连续推迟。Liang等[12]考虑了有维修情况的航班恢复问题。Lan等[13]和田文等[14]分别对航班延误时间序列特性和航班延误传播的分析方法进行了研究，构建航班延误时间序列并构建了基于航空演化网络的延误传播模型。刘盼等[15]研究了航班延误及储备员工分配的机组分配问题。

综上所述，现有研究成果为进一步研究受扰航班恢复计划问题提供了借鉴和思路。在关于受扰航班恢复计划问题研究方面，可以看出较少研究同时考虑了飞机资源短缺、机场关闭、计划外的飞机维修、旅客等多因素的情况，更少有研究同时采用航班延误(维修不允许延误)、航班取消、航班交换等多种恢复措施。本文以航空公司原航班计划受干扰后需要快速恢复为研究背景，基于航空公司遇到的实际情况，对飞机航线恢复问题进行分析，建立数学优化模型，设计适用于该模型的算法，并结合实际案例进行测试，对算法求得的结果进行对比分析，为航空公司的运行决策提供有力的支持。

1 问题描述及数学建模

1.1 问题描述

每个机场有固定的开始时间和关闭时间，在机场的可利用时间段内安排航班任务和维修任务，航空公司根据机场、飞机以及航班需求等信息制定正常的航班计划。但是在航空公司的运营中，导致航班延误甚至取消的原因有很多，比如飞机机械故障、机场关闭、机组人员缺乏、恶劣天气影响等。

文中只考虑造成航班受扰的两个主要因素：机场关闭、飞机维修(计划外机械故障引起)，机场关闭意味着在一段时间内，飞机不允许离开或者达到关闭的机场，然而已经达到该机场的飞机可以在机场内完成维修任务(如果有维修需求)，在这里我们把航班和维修都当成是飞机的任务(飞行任务和维修任务),如图1所示。

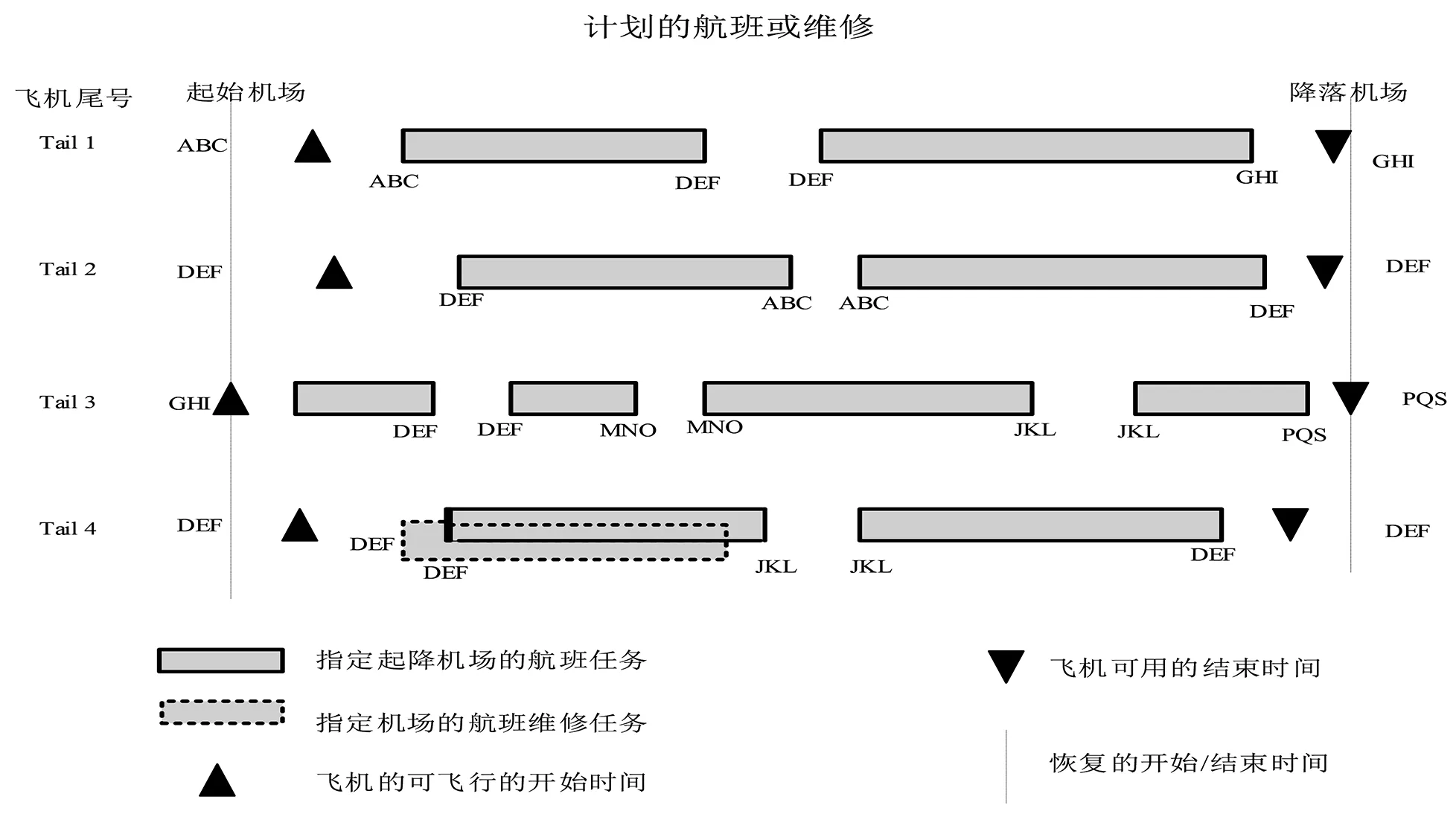
图1 计划的航班或维修

在实际情况中，如果一架飞机出现计划外的故障，就需要对飞机进行维修(计划外的)。飞机维修需要在固定的机场和固定的时间段内完成维修任务，这样的情况本文称为非计划的维修任务。因为维修不是计划内的，飞机一旦选择维修，就有可能出现原航班计划中的飞行时间与维修时间重叠的情况，因此该架飞机在维修时间内不能执行任何航班任务。本文中飞机维修任务的时间窗是开集，意味着飞机一旦降落到指定的机场就可以马上进行维修，同理维修任务一旦完成，飞机可以及时起飞离开机场。因此，如果出现机场关闭或者维修任务，原有的航班计划就会出现冲突，比如航班原有的降落机场不能降落，飞机维修不能执行接下来的航班任务等，造成原航班计划不可行的情况，为了恢复航班计划的可行性，同时降低损失，则有推迟航班、交换航班、取消航班以及取消维修四个选项。其中，推迟航班：航班实际的“起飞和到达时间”与“原航班计划中航班的起飞时间和到达时间”不一样。例如，图2列出了飞机尾号为Tali 1的一个航班任务信息，即航班5183的原航班计划的信息。在实际情况中，这个航班可能会因为上述一些原因延误一段时间，比如，延误30分钟，那么航班的起飞时间就变成同一天的上午8∶05和10∶25，其他信息保持不变。全球规定的航班推迟时间阈值为180分钟，意思就是航班5183可以在0-180分钟内选择任意时间段的推迟，但是航班推迟是有惩罚的，要求推迟时间越短越好。交换航班：在原航班计划中每个航班都有指定的飞机去执行，即飞机尾号，如果一个航班最后被执行的飞机尾号与原计划航班的飞机尾号不一样，我们就称该航班为交换航班。航班交换是有惩罚的，要求航班交换的数目越少越好。取消航班：如果一个航班不能指派给任何一架飞机去执行，那么就取消；取消维修：如果维修任务无法指定给原计划的飞机，那么只能取消，这里要注意的是维修任务是不能指派给别的飞机的。取消航班或者取消维修的惩罚相对于上面其他恢复措施惩罚更严重，要求取消的个数越少越好。

图2 航班信息

本文研究的受扰航班恢复问题，目标是尽快恢复受扰航班和尽量减小航班延误时间、航班取消个数、维修取消个数以及航班交换个数，这些恢复措施有不同的惩罚系数。除了上述提到的情况，在研究飞机路线恢复问题时还要遵守以下的约束：(i)任何时候，最多只能有一个任务(航班或者维修)安排给一架飞机；(ii)每一架飞机刚开始都有一个指定的可获得机场，那么该架飞机开始执行任务(航班或者维修)时必须和任务的开始机场相匹配；(iii)指派给同一架飞机的任何两个连续的任务(航班或者维修)应该“首尾”相连，也就是说，前面任务完成时的机场和后面一个相连任务开始时的机场是一样的；(iv)对于每一个机场尽量保持机场飞机数目的平衡，例如，图1中在最后的降落机场“DEF”上有两架飞机，那么在接下来的飞机航线恢复问题的可行解中，当恢复问题完成时尽量保持有两架飞机降落在机场“DEF”上，然而此约束为软约束，如果有机场最后没有保持这个平衡，我们会在目标函数中添加惩罚；(v)每架飞机的第一个任务(航班或者维修)的开始时间不能早于该飞机可飞行的开始时间，同理，最后一个任务(航班或者维修)的结束时间也不能晚于该飞机的结束时间；(vi)对于每架飞机所执行的连续的两个航班任务之间都必须满足一个周转时间(30分钟)，这个周转时间是飞机为执行接下来的航班任务做准备，包括旅客下机、食物补给、清洁等。

1.2 数学建模

在这里我们基于飞机的航线建立一个整数规划模型以更准确地描述问题，首先，给出模型的参数定义。

集合

P-飞机集合;R-飞机飞行路线集合;F-航班集合;A-机场集合;MT-维修任务集合

参数(下面的参数都属于整数)

机场方面的(原计划中)：

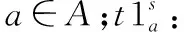
飞机方面的(原计划中)：

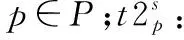
航班方面的(原计划中)：

维修方面的：

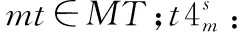
决策变量

xpf：如果航班任务f最后指派给了飞机p去执行则为1，否则为0，f∈F,p∈P;

ymt：如果维修任务mt在给定的机场被完成则为1，否则为0，mt∈MT;

zf：如果航班任务f属于交换航班则为1，否则为0，f∈F;

πf：如果航班任务f被取消了则为1，否则为0，f∈F。

目标函数：

(1)

约束条件：

(2)

ymt≤1,∀mt∈MT

(3)

(4)

(5)

(6)

(7)

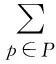
(8)

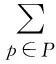
(9)

xpf∈{0,1},∀p∈P,f∈F

(10)

ymt∈{0,1},∀mt∈MT

(11)

zf∈{0,1},∀f∈F

(12)

该模型中，目标函数(1)最小化航班取消成本、航班交换成本、航班延误成本、维修取消成本以及机场飞机数目不平衡成本的惩罚的总和；约束(2)要求每一个航班要么被安排到某一架飞机，要么被取消；约束(3)维修任务也是，要么被完成，要么被取消，这里要注意，维修任务不能交换也不能推迟；约束(4)要求任何一个航班的延误时间不能大于规定的最大延误时间；约束(5)要求任意两个连续航班之间的周转时间不能小于TT；约束(6)保证每架飞机所飞行航线中的第一个航班的起飞机场与该飞机的可飞行开始机场一致；约束(7)表示每架飞机所飞行航线中任意两个连续的航班要满足前航班的结束机场与后面一个航班的开始机场相一致；约束(8)表示原航班计划中每个机场最后降落的飞机数目；约束(9)表示恢复航班计划之后每个机场最后降落的飞机数目；约束(10)～(12)表示决策变量是0-1变量。

2 模型的求解算法

2.1 基于满足不同中断要求的启发式序列延迟算法求解可行解

此算法的目的是针对原航班计划遇到干扰时进行恢复，使恢复之后得到一个可行的飞机航班计划表。在算法求解的过程中，首要目标是产生一个可行解，在此基础上尽可能获得较优的解。启发式序列延迟算法是基于满足不同的中断情况对航班进行推迟或者取消。首先，选择一个原计划航班中的航线，当飞机遇到维修任务或者机场关闭的情况时，筛选出受影响的航班；其次，调整这些航班使其不再受影响，对于满足约束条件的航班给予指派，对于不满足约束条件的航班进行取消，由于相连航班要求满足“首尾相连”的特性，所以航班的取消会成对出现，当这个航线处理完之后转入下一个航线。

2.2 构建启发式算法的基本框架

飞机航线恢复问题是非常复杂的组合优化问题，上面我们针对该问题建立整数规划模型，考虑精确算法求解此问题时，需要对每一架飞机p∈P给出所有的可能路线，然而由于实际中的飞机航线恢复问题涉及的约束繁多、规模庞大，问题的搜索空间也非常大以及算法的求解过程非常耗时等，使得精确算法在实际问题求解过程中不切实际，达不到实时调整的要求。

构建启发式算法，是两种常用的启发式算法之一。算法描述如下：

①根据输入的航班信息，对同一航线的航班根据其起飞开始时间的大小做非减排序，同时，根据机场关闭信息和航班信息，找出一定被取消的航班(由于机场关闭这些航班延误时间大于给定的最大延误时间阈值，所以此时只能取消)；

②先选定一架飞机，然后开始选择航班，在选择航班中，飞机可能会遇到维修任务和机场关闭的情况，根据维修以及机场关闭的信息，航班做出相应的调整，否则取消航班，当这架飞机的航班都被安排完毕，则结束该架飞机的飞行路线，并转向下一架飞机；

③当所有的飞机和航线都被安排完毕，则算法停止，输出恢复后的可行航班计划。

在实际情况中，由于飞机的维修对旅客的安全有着极其重要的影响，因此飞机的维修任务取消的惩罚成本在所有的惩罚成本中是最大的，所以本文选择以维修任务优先的构造启发式算法，即当飞机起飞之后遇到维修任务的干扰且不能满足延误条件时，就优先安排维修任务，删除不能满足延误条件的航班。

3 实验

3.1 案例背景以及案例数据

本文中的程序使用C++编码，采用2GB内存和2.8GHz英特尔双核处理器进行测试运行。为了验证本文所提出的构建启发式优化算法的有效性，本文结合S航空咨询公司实际案例进行测试，即测试数据来源于S公司的真实数据。本文中测试了9个不同案例来反映实际中可能遇到的情景，其中，每个案例对应一种场景，每个场景的中断情况有所不同，并且每个案例对应的恢复措施的惩罚成本也各不相同。虽然这些成本有所不同，但是在每个场景中，取消航班或者取消维修任务的惩罚成本都是最严重的。表2给出了每个场景中恢复措施的惩罚成本。其中，“F”与“P”分别表示航班数目与飞机数目，即“F24-P2”表示这个算例中有24个航班和2架飞机。表2中第一列是算例，后面的各列给出了不同飞机航线恢复措施的惩罚成本。另外，每个算例中航班的最大延误时间是180分钟(或者10800秒)、连续航班之间的最小周转时间是30分钟(或者1800秒)。为了清楚表示每个算例中遇到的扰乱情况，本节给出了每个算例的基本情况，如表3所示，在表3中算例 “F24-P2”遇到1个维修任务和1个机场关闭的情况、算例“F33-P10”遇到16个维修任务、算例“F43-P3”遇到1个机场关闭的情况、算例“F53-P4”遇到1个维修任务和1个机场关闭的情况、算例“F59-P16”遇到23个维修任务、算例“F95-P12”遇到1个机场关闭的情况、算例“F417-P85”遇到25个维修任务和1个机场关闭的情况、算例“F586-P44”遇到24个维修任务和1个机场关闭的情况、算例“F638-P44”遇到29个维修任务。每个算例的维修任务和机场关闭的具体情况也所不同，比如维修任务指定的飞机或者完成这个维修任务需要的时间各不相同。

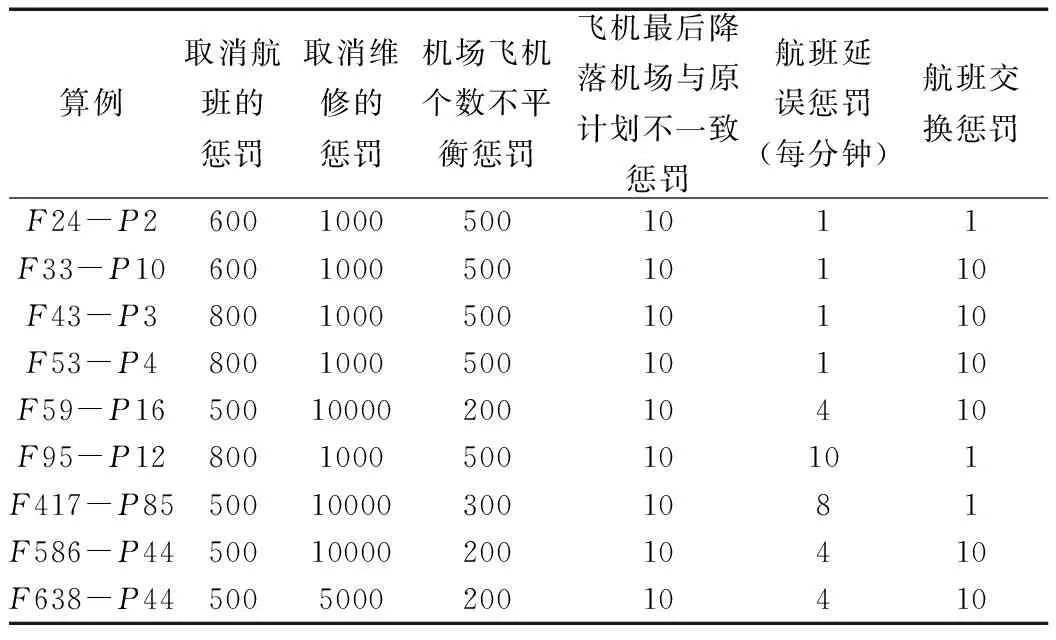
表2 恢复措施的惩罚成本

表3 每个算例的基本情况

3.2 优化方法测试结果以及与启发式序列延迟算法的对比

本文选取的案例数据具有代表性，案例的规模大小不同，每个案例所涉及的不同受扰中断情况也更加贴近现实。通过启发式序列延迟算法和构建启发式算法去求解这些算例，由于飞机的维修任务惩罚成本最大，航空公司实际运营中也是以维修为主，所以本文在算法构造上采用了以优先考虑维修任务为主的策略。

关于程序运行方面，程序使用C++编码，采用2GB内存和2.8GHz英特尔双核处理器进行测试运行。每个案例的测试时间都不超过5分钟，最短的只需要0.17分钟，因此，从时间上看，该算法完全满足公司在时间方面时效性的要求。首先，表4给出了构建启发式算法求解算例的结果，其中，第二列给出了目标函数值，其余各列给出了飞机航线恢复中恢复措施的采取情况。由表4第四列“取消维修数”可知，所有算例中的维修都被优先考虑。以算例“F53-P4”为例，原航班计划中包含53个航班、4架飞机，所有的航班和飞机信息中包含有6个不同的机场，分别用“1、2、3、4、5、6”表示六个机场，但是在原航班计划实施前遇到了维修任务和机场关闭的情况，其中，维修任务要求第四架飞机在第2个机场进行维修，维修时间为425分钟；机场关闭要求第2个机场在第“1336086000秒至1336100400秒”的时间段内关闭。维修任务的时间和第四架飞机航线内航班任务的时间有冲突，机场的关闭对这个时间段内航班(航班起飞机场或者降落机场是关闭机场的)有影响，比如航班编号为“2457074”的航班的起飞机场是机场“2”，起飞的时间正好在机场“2”的关闭时间段内，这就需要对原航班计划进行航班恢复，结果显示飞机航线恢复之后的可行计划中取消了4个航班，有两个机场的飞机数目没有保持平衡，有2架飞机与原计划飞机的位置不一样，有20个航班进行了交换，所有的航班总共延误了145分钟。

表4 航班恢复情况

表5 算法分析对比

4 总结

本文研究了基于多因素不确定环境下受扰航班计划的恢复问题，其主要任务是在考虑干扰因素的情况下尽量完成航班任务，形成可行的飞机航线，即以最小化航班取消、航班交换、航班延误、维修取消以及机场飞机数目不平衡惩罚成本的总和为目标。结合S航空公司实际操作的案例，针对该问题建立符合航空公司实际调整规则及制度的数学模型，根据不同的策略，通过对比分析，设计有效的构建启发式求解算法，并通过S公司实际的案例进行测试分析，分析结果显示，构建启发式算法比“算法1”的结果平均提高了32.47%，在求解规模上完全达到航空公司实际应用规模的受扰航班恢复问题，并且在时间上完全符合实际操作的实时性要求，本文提出了适用性较高的算法，为航空公司的运行决策提供有力的支持。

本文研究的内容只是航空公司运营计划中的一部分，它与机组人员排班、机型分配以及乘客安排等其他环节紧密相关，因此对于航班恢复问题还需要更加深入的研究。同时，本文研究的内容具有一定的局限性，后期还可以进一步研究，设计出综合的优化方案，提升解的质量。