基于Crank-Nicolson差分法的KdVB方程有限元解的误差分析

姚富霞

(延边大学 理学院， 吉林 延吉 133002)

0 引言

本文考虑具有如下初边值问题的Korteweg-de Vries-Burgers (KdVB)方程：

ut+εuux-νuxx+μuxxx=0,x∈Ω, 0≤t≤T;

(1)

u(0,t)=u(L,t)=0,x∈Ω, 0≤t≤T;

(2)

ux(0,t)=ux(L,t)=0,x∈Ω, 0≤t≤T;

(3)

u(x,0)=u0(x),x∈Ω.

(4)

其中Ω=[0,L],ε、ν、μ为正数，x是空间变量，t表示时间变量.

KdVB方程是一类同时包含阻尼和色散的非线性系统方程[1]，因其在物理学和数学中具有广泛的应用，因此受到学者的关注.1970年， Johnson首次研究了KdVB方程在相平面上的行波解，并给出了解的渐近展开式[2].1985年， Bona等证明了KdVB方程有界行波解的存在唯一性[3].随后一些学者利用有限元[4]、tanh方法[5]、指数有理函数法[6]和有限差分格式[7]等方法求解了KdVB方程的数值解.

Crank-Nicolson差分法因具有无条件稳定性和二阶隐式的差分格式，因此近年来被广泛地应用于偏微分方程的数值计算中.在文献[8]中，作者采用Crank-Nicolson差分格式求解了Kdv浅水波方程的定解问题，并从理论上分析了定解问题的截断误差、稳定性和收敛性，同时通过数值实验验证了Crank-Nicolson差分格式的有效性.在文献[9]中，作者建立了一种兼具稳定性和并行性的交替分段Crank-Nicolson格式，并通过理论分析得到了此差分格式解的存在唯一性、稳定性和收敛性.在文献[8-9]研究的基础上，本文利用Crank-Nicolson差分法对KdVB方程和KdVB方程降维模型的时间变量进行离散，并分别给出KdVB方程和KdVB方程降维模型的H1误差估计.

1 准备工作

(5)

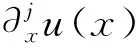
(6)

设M∈N+为正整数， {Τh}h >0为空间变量的网格，h=L/M为网格尺寸.记网格节点为xj=jh,j=0,1,…,M.记子区间为Ij=[xj,xj +1],j=0,1,…,M-1.设Pr(I)为区间I上次数不大于r∈N+的多项式空间.为了求方程(1)—(4)的近似解uh， 定义Sh(Ω)为:

(7)

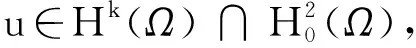
(8)

为了误差估计，在Sh(Ω)上引入Ritz投影Ph， 使得对于v∈H1(Ω)， 有:

((Phv)x,χx)=(vx,χx), ∀χ∈Sh(Ω).

(9)

引入以下3个引理，证明过程可参考文献[10-11].

引理1在式(9)的条件下，当v,vt∈Hk(Ω),k>r，Phv∈Sh(Ω)时，下列不等式成立：

(10)

(11)

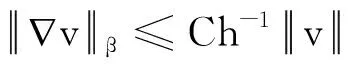
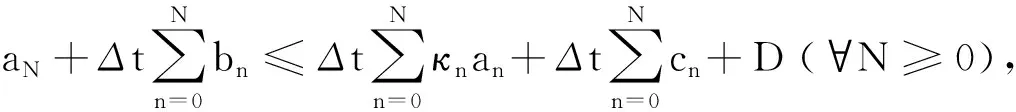
2 全离散的Crank-Nicolson有限元解的误差估计

(12)

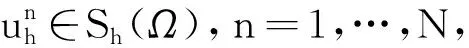
(13)

将误差en分解为如下形式：

(14)

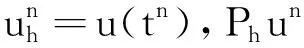
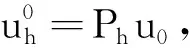
(15)

其中C是与h和k无关的常数.

证明因已知ξn的估计值，因此可以用ξn来估计ηn.用式(12)减去式(13)可得如下等式：

(16)

(17)

再利用Young不等式和引理2可得：

(18)

整理上式可得如下不等式：

(19)

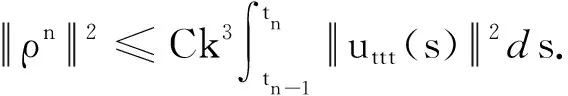
将上式从n=1到N求和可得：

选择适当的k使(1-Ck)≥0， 则有：

(20)

3 基于POD方法的Crank-Nicolson有限元解的误差估计

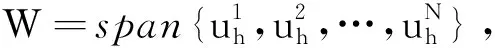
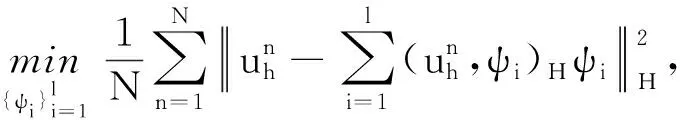
引理4[13]若un∈Hr +1(Ω)和Pdun∈Sd(Ω)， 则有如下不等式：

(21)

在式(6)中，若v∈Sd(Ω)， 则可得：

(22)

(23)

将误差en分解为如下形式：

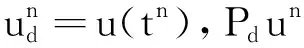
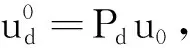
(24)

其中C是与h和k无关的常数.

证明用式(22)减去式(23)得到如下等式:

(25)

再利用Young不等式和引理2可得：

(26)

对式(26)进行整理可得如下不等式：

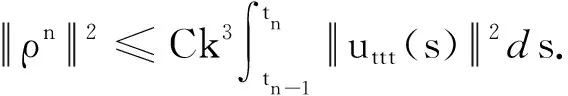
将上式从n=1到N求和可得：

选择合适的k使1-Ck≥0， 则有：

(27)