借形识数 逐级抽象

“数的认识”这一领域主要指向的核心素养是数学抽象思维，而小学生主要以具体形象思维为主，那么如何借“形”让学生经历逐步抽象出“数”的过程就至关重要。接下来我以苏教版教材三年级下册《小数的初步认识》为例，谈谈自己的一些思考。

一、巧用“直条”，识小数

（一）直条充当“米尺”，认识零点几的小数

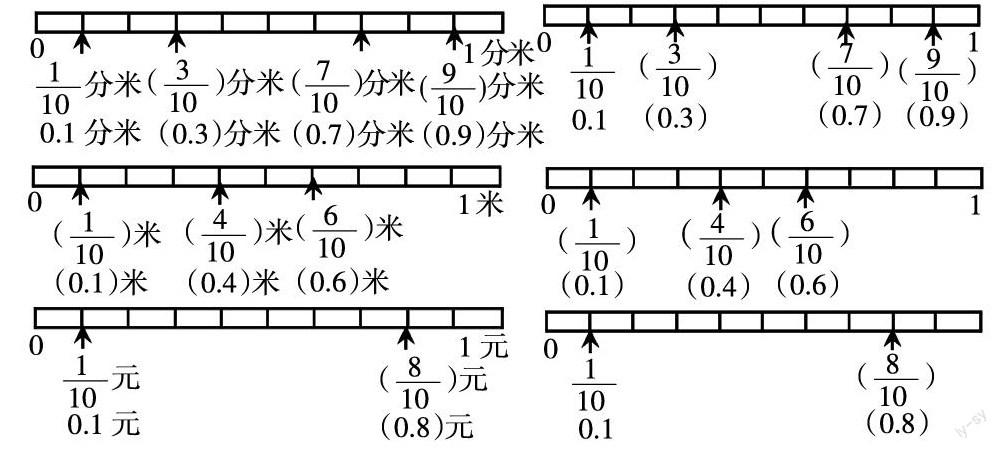
华罗庚曾说过：“数来自数，量来自量。”通过用直条表示米尺，测量小棒的长度，思考讨论1分米是几分之几米？交流引出：1米=10分米，1分米是1米的_______，是_______ 米。指出：_______  米还可以写成0.1米，0.1米也表示_______ 米。在此基础上，用带有一组数的直条测量课桌面的长和宽，认识0.4米和0.6米。

就数学本质而言，小数是一类特殊的分数，是十进分数的另一种形式。结合学生的学习经历，让学生在直条上找一找“□/10米和0.□米”这样一组组的数，用数学的眼光观察这些一组一组的数，学会用数学的语言表达自己的发现，突出“□/10米和0.□米”的联系。

（二）直条化身“1元”，认识几点几的小数

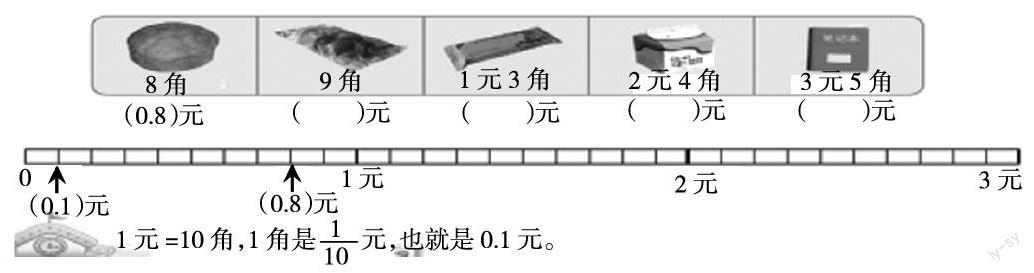
直条和米尺，这两者形似，也因此学生很容易建立联想。基于学生在上述学习中积累的活动经验，引发学生思考“用这根1米的直条量出黑板的长度，不够该怎么办”，使学生在脑海中自然想象出在原有直条的后面再接一根直条的画面，在此基础上，告诉学生此时的这根直条表示1元，从长度情境迁移到元、角、分的情境，追问2元在哪里，3元呢？并把表示1元的直条平均分成10份，从而引出1元=10角，1角是元，也就是0.1元。

结合学生的生活经验，借助直条图的直观形象，学生用小数在括号里表示商品价格，在直条图上标一标。学生通过在已有的直条后面自己添加直条表示出3.5元，想象3.5元后面的小数，学生的思维一次次碰撞，在数的过程中认识更多的小数，初步体会小数的个数是无限的。

二、数形结合，悟小数

（一）观察比较，建构一位小数的认识

学生经历了1米直条图、1元直条图，在练习时加入1分米直条图的填空，重温把十分之几写成一位小数的活动，让学生继续体验一位小数的意义。进而启发学生比较“1米直条图”“1元直条图”和“1分米直条图”相同的地方，学生通过观察比较具体情景下的三幅直条图，体会“情景不同，但只要把1平均分成10份，这样的1份或几份都可以用十分之几的分数表示，也可以写成一位小数”。在直条上隐去单位，从而帮助学生实现一位小数的认识建构。

（二）直观变化，理解一位小数的含义

上述练习从用“数量”表示的直条抽象到用“数”表示的直条，在此基础上让学生再根据直条图涂色部分的变化按序数出小数，形成比较完整的认识。并结合空白的正方形图，交流怎样分别表示0.1，0.5和0.9，由直条图数小数，到看小数描述正方形图，从不同角度不断强化学生对一位小数含义的认识。

紧接着引发学生思考在0至1的线段上能表示小数吗？（把线段十等分）說出线段上的点表示的小数。

通过借助直条、正方形、线段直观变化“1”的表示，帮助学生进一步抽象，初步形成“十等分模型”，理解一位小数的本质含义。

（三）抽象概括，完善小数的认识

数轴上的数才是真正意义上的数，最后通过线段0至1的不断延伸，引出数轴，回归数轴，让学生在数轴上写一写，数一数，在活动中增强学生的数感。

结合数轴上标出的数，让学生分成两类，渗透分类思想，并用不完全举例归纳指出自然数、整数及小数的概念，比一比小数相同的地方，让学生在比较中认识小数的各部分名称，完善对小数的认识。

虽然数是抽象的，但若借助“形”识数，以 “形”作为载体，在“形”上多思考研究，数形结合，逐级抽象，那“数”也就没那么抽象了。

作者简介：蒋海兰（1987—），女，汉族，江苏苏州人，本科，中小学一级教师，研究方向：小学数学。