结合卷积神经网络的DFT-Like信道估计算法

谢思琪，赵宏宇

（西南交通大学，四川 成都 611756）

0 引言

随着物联网、车联网（Vehicle to Everything，V2X）和5G及其下一代通信技术的发展，为了支持快速增长的移动互联网流量需求，现代无线网络的主要功能是为用户提供高速的数据速率。在这种环境下，传统的信道估计技术已不再适合。

目前研究人员已将深度学习（Deep Learning，DL）应用于信道估计[1-9]、信道检测[1,7,8,10]和信号分类等问题中。其中，在信道估计领域，人工智能得到了极大关注。文献[2]提出的符号检测器最小冗余（Symbol Detector Minimum Redundancy，SDMR）网络跟踪信道特性，既减少了循环前缀的冗余，又提高了恢复的精确度，虽然其性能略优于线性最小均方误差（Linear Minimum Mean Square Error，LMMSE），离性能上限还有1 dB的差距。文献[3]提出的ChannelNet把带估信道矩阵转化成低分辨率图，用超分辨率网络获得时频信道矩阵，然而，该算法性能仅接近最小均方误差（Minimum Mean Square Error，MMSE）方法，且不知道最佳导频模式。文献[4]中提出的接收机包含残差结构中级联的深度可分离卷积，改善了信道性能，然而，结果略差于LMMSE方法。

由于之前TensorFlow、Keras等深度学习平台不支持复数神经网络（Complex-Valued Neural Network，CVNN）[6,11]，因此，上述文献多是将待估计的信道信息简单地视为实数，然而无线信号及滤波器是使用复数定义的。部分研究使用深度学习算法[1,2,5,8]，其估计的误差性能不能优于理想的LMMSE方法。此外，现有的一些基于深度学习的信道估计算法[1,2,4]和通信自动编码器（Communication Auto Encoder，Com-AE）[9]仅限于依赖（逆）离散傅里叶变换（Discrete Fourier Transform/ Inverse，DFT/IDFT）来处理波形，这限制了网络的扩展性。

基于这些因素，本文提出一个基于卷积神经网络的信道估计算法，利用复数残差信道估计网络（Complex-valued Residual Estimation Network，Cv-ReEsNet）和卷积估计出信道的频域响应，设计了DFT_Like网络学习转换正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）波形，并通过在衰落信道下的实验，验证了算法性能。

1 系统模型

OFDM系统在衰落信道中具有带宽效率高、鲁棒性好等优势，其信道估计仍是现代通信网络和5G的研究重点。因此，本文考虑一个单输入单输出（Single-Input Single-Output，SISO）链路上N个子载波的OFDM系统。OFDM符号的长度为S=N+Ncp，其中Ncp为CP的长度。输入信号可以从M-正交调幅调制（Quadrature Amplitude Modulation，QAM）转换为并行数据流X。然后利用N点IDFT或者逆快速傅里叶变换（Inverse Fast Fourier Transform，IFFT），将信号从频域X转换到时域x。加入CP后，无线信道的模型为：

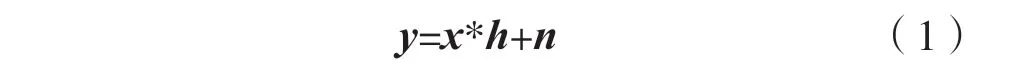
式中：向量x,y,n∈CSF×1（去除CP时，x∈CNF×1）分别代表时域的发送信号、接收信号和时域白噪声，信号包含振幅和相位信息；C为复数集；*为卷积；F为每个相干时隙OFDM符号数；向量h=[h(0),h(1),…,h(L)]T∈CL×1为时域信道系数；L为信道滤波器长度。在多路径衰落信道中，信道系数随子载波而变化，因此信道表现出频率选择性，同时信道会产生码间干扰（Inter-Symbol Interference，ISI）效应。

本文采用具有导频的辅助信道估计，使用长期演进（Long Term Evolution，LTE）系统的[12]导频插入模式，它与格状导频模式一致，既适用于频率选择性衰落，又适应快衰落。基于导频的信道估计通常用于获取完整的信道状态信息（Channel State Information，CSI）。在传统的估计方法中，最小二乘（Least Squares，LS）方法和LMMSE方法是两种典型的方法。LS方法虽然简单，但其估计精度往往不令人满意。为了获得更精确的CSI，还可用LMMSE方法[13]：

式中：=X-1Y为最小二乘算法获得的信道响应；RHH=E{H*H*H}为基于实际信道实现H*的频域协方差矩阵；为近似的信噪比；β为特定调制下的定义常数。LMMSE需要先验信道信息RHH和噪声方差先验知识，在实际中不可实现，且复杂度也 很高。

2 算法设计

2.1 模型结构

本文模型包含了线性激活的残差连接（Residual Connections）网络和跳连（Skip Connection）网络的新结构。多数研究简单地分开处理复数的实部和虚部，很可能会影响深度神经网络（Deep Neural Network，DNN）充分利用信号的相位和振幅的关系，从而增加复杂性、降低性能且限制其可解释性。与现有的由全连接层和非线性激活组成的深度学习方法相比，所提方法提供了复数神经网络的表达，包含全连接层和复数卷积神经网络，且大多数使用线性激活。此外，设计的DFT-like网络能够学习处理高级波形，证明了DL在学习除OFDM外其他高级波形，如滤波器组多载波（Filter Bank MultiCarrier，FBMC）的能力，适用于5G和下一代新型通信系统。本文所提算法的网络结构如图1所示，其中灰色块为复数域，白色块为实 数域。

图1 算法的网络结构

2.2 基础接收器

首先设计一个基于加性高斯白噪声（Additive White Gaussian Noise，AWGN）信道的基础接收器。该网络模型输入待估计的发送信号，该信号随后被基本接收器转换为估计的软比特。该模型算法流程包括3个步骤：

（1）输入尺寸为[B,F,S]的时域符号。开始为可选操作，用于加入或去除CP；然后设计一个复数卷积层转换时域符号，尺寸大小为N×S×1（去除CP时为N×N×1）。

（2）特征提取，用于提取OFDM帧。由一层全连接神经层实现，得到数据尺寸为[B,D,2]。

（3）解调。将复数的IQ数据转换成软比特。将复数IQ数据分离为2个实数，使用实数LRelu激活函数，用于减少可训练参数的数量；然后，将原始的IQ数据和LRelu激活的输出相结合设计成跳连网络，得到输出数据尺寸为[B,D,4]；再输入给最终的全连接神经网络（Fully Connected Deep Neural Network，FC-DNN）层；最后，调整输出尺寸并使用softmax激活，得到尺寸为[B,D,1,2]的软位流输出，即用2个实数表示每个位（例如0和1的对数似然）。

2.3 基于卷积神经网络的信道估计

为无线物理层（Physical Layer，PHY）卷积神经网络的设计和分析提供CVNN的近似实现。忽略偏置和激活函数，一个复数神经元可以表达为[11]：

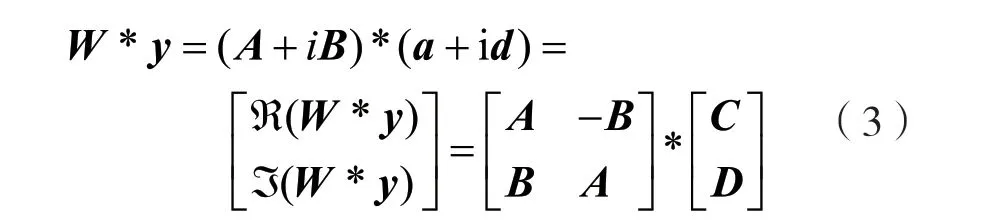
式中：输入向量y=a+id∈C，并且引入一个权重W=A+iB∈C，R(W*y)和ℑ(W*y)分别代表W*y的实、虚部。

在式（3）的基础上，一个复数层（尺寸fn×fs×fc，fn代表滤波器个数，fs代表形状尺寸，fc代表信道数）可由大小为2fn×fs×fc的高维实数层实现，如图2所示。

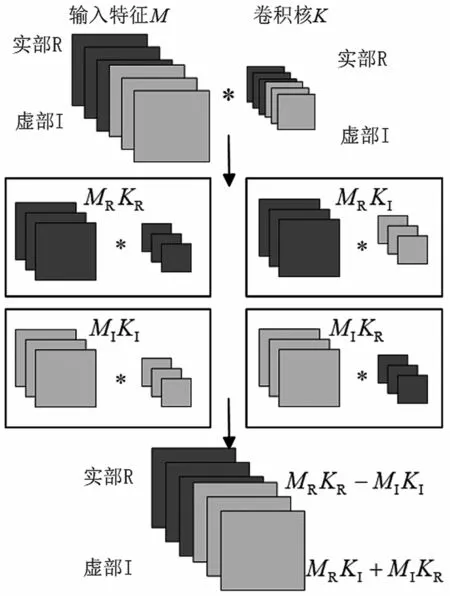
图2 一维复数卷积处理过程

均衡器的网络组成如图1左侧所示。该网络将时域接收信号ycp转换为待估计的发送信号x^cp。第一模块（第1～4层）是用于执行时域/频域变换。输入接收信号y∈CS×N，其输出形状为[B,F,N]，B代表小批（Batch）迭代时隙。然后，通过一个DFT-like网络，尺寸为N×N×1，即长度N的N个1D滤波器，将时域ycp转换为频域Y。复数卷积神经网络结构包括复数批量标准层、复数卷积层等结构。该网络自定义为layers_conv2d_complex，如算法1。

第二模块用于估计信道频率响应，并实现信道均衡。第三模块（最后2层），利用复数Conv层设计IDFT-like滤波器执行频域/时域变换。第二模块主要包括多层FC-DNN、二维复数卷积网络以及复数残差网络。最后，通过复数除法实现频域信道均衡，如算法2所示，为部分伪代码。

算法的具体流程如下：

（1）设计一层FC层，尺寸为[B,P]。该层采用线性激活，用于对输入的OFDM帧Y定位和提取的导频P。然后，设计第二层FC层，尺寸为[B,P]，输入LS信道估计值，得到∈CFN×FN。

（2）跟踪3层FC层来估计先前估计信号的残差，尺寸为[B,P]，采用线性激活。其中，包含残差网络是一种优化的卷积神经网络[14]。ResNet能解决网络层数加深带来的退化问题，即提高模型的准确率。一个复数残差块模块的结构是直接由实数域残差网络的改进而来，如图3所示[11]。若该单元的输出为y=F(x)+x，当继续增加网络参数时，令F(x)=0可得y=x的浅层网络来达到最优网络。

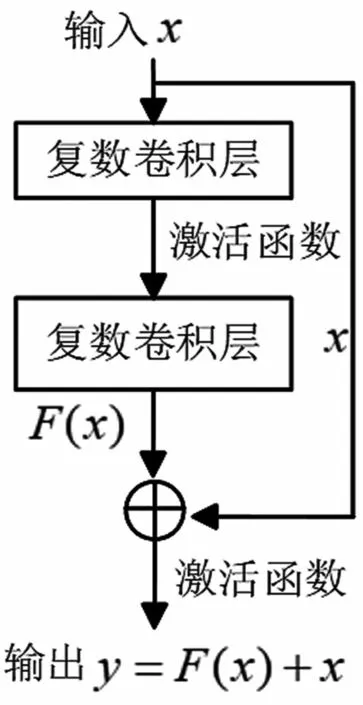
图3 复数残差块结构

（3）导频层、一阶LS估计和残差估计值均通过Concat函数组成跳接结构，然后送入下一个插值块。

（4）内插块包含3个FC层，尺寸为[B,F,N]。由于数字IQ信号实、虚部都有正负分量，因此，把复数的IQ数据当作两个独立的实数，使用tanh激活函数。

（5）通过layers_ conv2d_complex网络层，作为滤波器处理复数来得到，尺寸为1×(F,N)×1。输出的尺寸类似于LRA-LMMSE[11]的二维滤波器(F,N)，计算方式为：

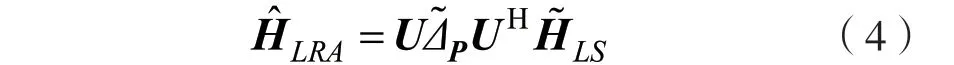
式中：U为带近似的协方差矩阵奇异向量的酉矩阵；是包含对角项δk的矩阵的特征分解值。则有：

2.4 模型训练

模型的训练过程和训练设置如图4和表1所示。其实验环境为，CPU处理器AMD Ryzen 7 4800U，显卡AMD Radeon Graphics，操作系统WINDOWS 10，内存16 GB；编程环境分别为MATLAB R2018a和基于Python3.6编程语言的Pycharm2020.2；框架为TensorFlow 1.1.12。参数在每次迭代中，通过遗留的OFDM发射器和信道模型生成新的随机比特流（标签），并将其转换为训练数据。网络采用二阶段训练，首先，在AWGN信道训练基本接收器；其次，加载已训练好的AWGN模型插入在加入衰落信道的均衡器网络之后，分别进行图形编辑和训练，利用网络可训练超参数学习系统的信道状态信息，提高误码率性能。

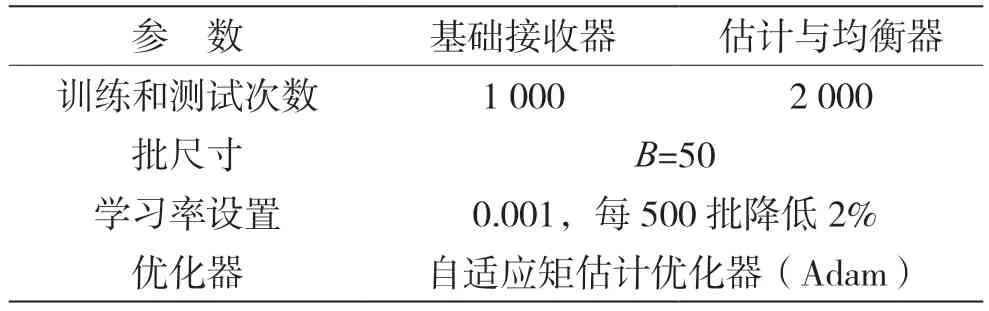
表1 训练设置

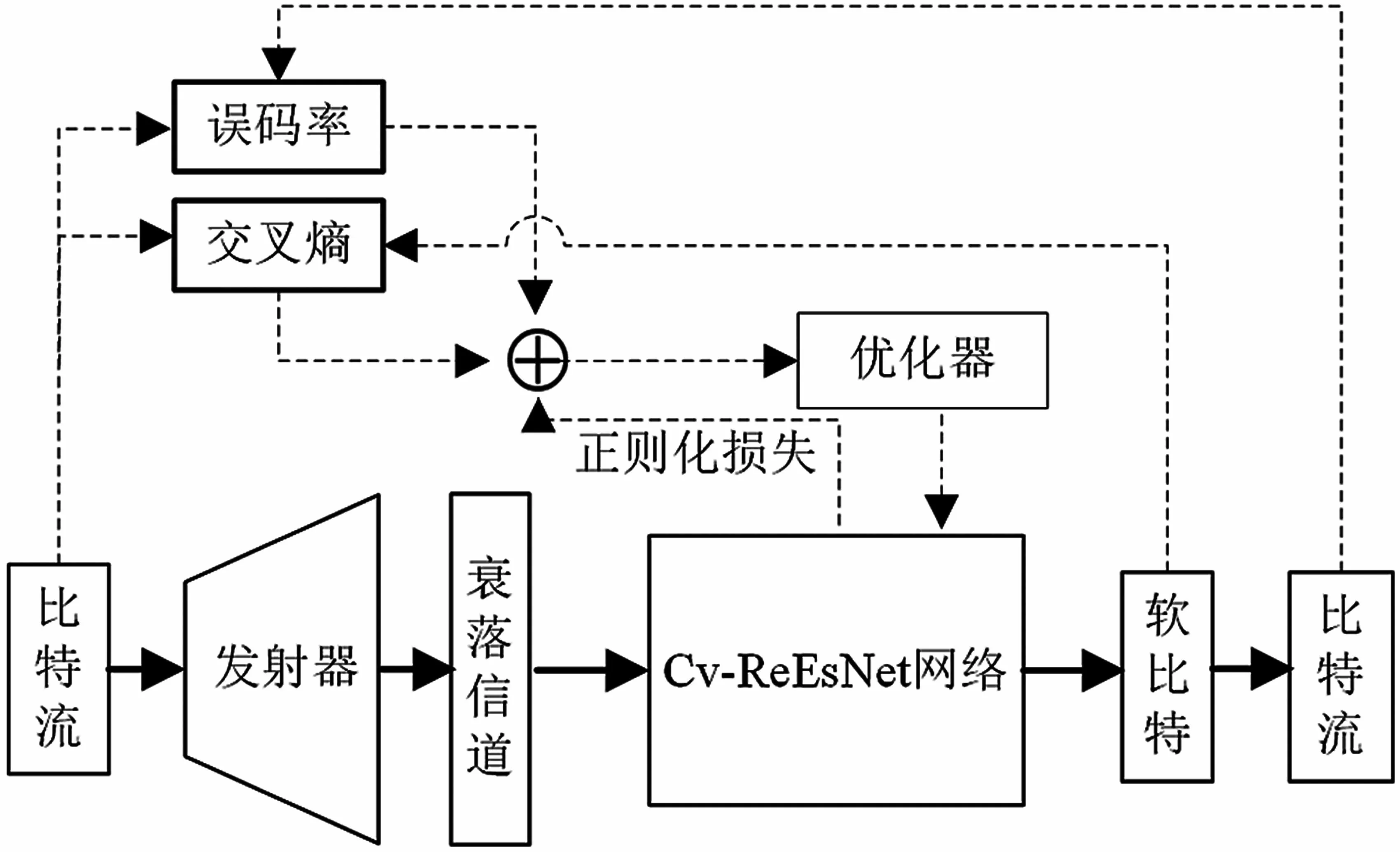
图4 网络训练过程

在MATLAB环境下，在线随机生成二进制流b=[b1,b2,…,bB]T，由发射器将其转换为时域符号。然后在发送信号xcp中创建增加衰落和噪声，得到包括CP在内的同步时域接收传输位：

式中：Ω为Cv-ReEsNet的可训练超参数集。

设计的损失函数L(b,,Ω)代表交叉熵（Cross Entropy，CE）损失和正则化损失（regularization Loss，Lreg）的加权和，计算方式为：

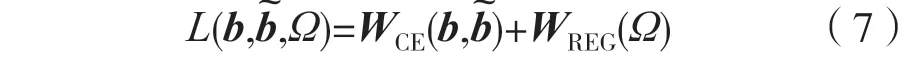
式中：b为训练数据ycp对应的标签；为模型输出的软比特位。输出比特硬判决得到的。提出的端到端损耗函数既能防止训练中梯度消失，又能使用混合信噪比和衰落模型平滑损失。

3 仿真分析

在本节中，将与其他同类信道估计算法以及传统信道估计方法进行比较，评估所提频域信道估计方法在不同环境下的估计性能。评估的OFDM系统的仿真如表2所示。

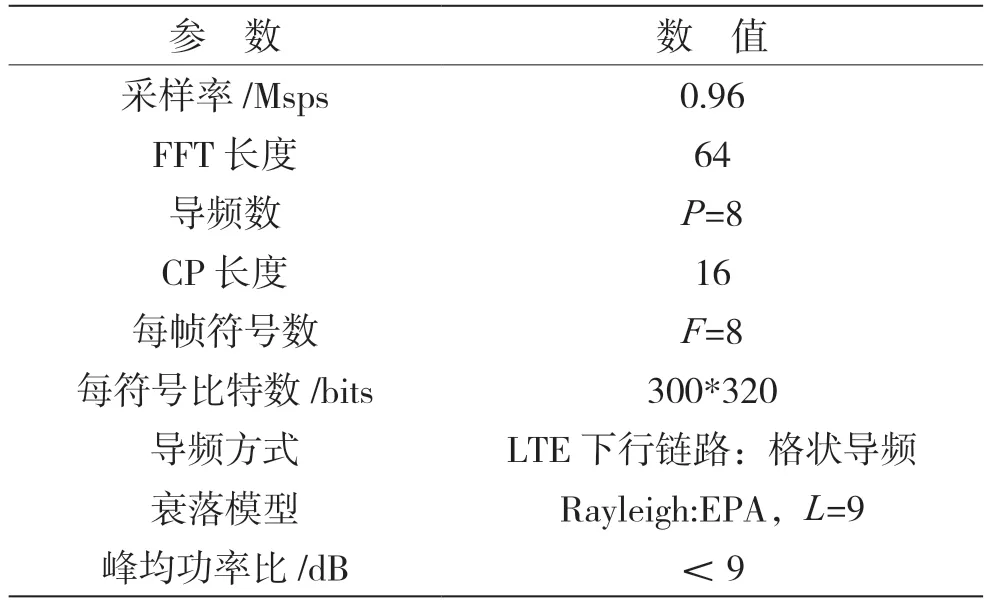
表2 OFDM系统仿真设置

3.1 误码率

对本文算法进行评估，图5是不同调制下Cv-ReEsNet的CE误差性能。每个外部训练迭代包含200个小批量，从−10 dB到20 dB，每个信噪比点的测试数据为300个相干时隙。由图5可知，首先模型能够快速拟合，其次在多次迭代中缓慢下降，到达一定的信噪比后稳定至0.32，模型得到了较优的训练。图6是在信噪比−10～20 dB中BPSK、QPSK、8QAM和16QAM调制下加入CP的Cv-ReEsNet的误码率（Bit Error Rate，BER）对比。由此可见，Cv-ReEsNet能迅速改善误码性能，但是增加调制级数性能有略微下降。

图5 不同调制下Cv-ReEsNet的CE性能

图6 不同调制下Cv-ReEsNet的BER对比

图7给出了BPSK调制下的Cv-ReEsNet方法与其他4种方法误码率性能对比。结果表明，当信噪 比（Signal-to-Noise Ratio，SNR）≤5 dB时，Cv-ReEsNet与需要信道协方差矩阵先验信息的理想的LMMSE相比性能略好。Cv-ReEsNet可以从数据中充分学习信道统计信息。在加入CP条件下，本文方法性能整体优于理想的LMMSE约1 dB。在低到中信噪比范围内，Cv-ReEsNet几乎与perfect曲线重叠，但在高信噪比下性能也有所下降。可见，接收器能够利用CP中所携带的冗余信息来获得性能增益。

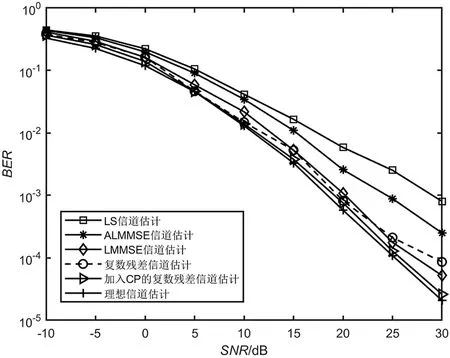
图7 BPSK调制下Cv-ReEsNet与传统方法BER对比

3.2 模型对比

本文还测试了其他实验，用于证实Cv-ReEsNet的优势。首先，验证了用两个分离的Conv层处理实部和虚部的简化实现替换C-Conv层，模型不能成功训练，BER始终为0.31。其次通过实验，笔者发现相似的模型如果没有残差分量和跳跃连接，性能会明显变差。此外，与其他简化模型进行了对比，如图8所示。将3.3节的算法2的layers_conv2d_complex层都改为实数网络模型或者删除，结果表明只有IQ向量分开处理不能取代本文方法的组合，复数神经网络比实数神经网络有更优效果。本文同样证实了文献[1]中的结论，如图9所示，设置信噪比为0～25 dB，FC-DNN可以在中低信噪比下匹配MMSE，总体误码率高于理想信道估计1～2 dB，显然没有优于本文方法。

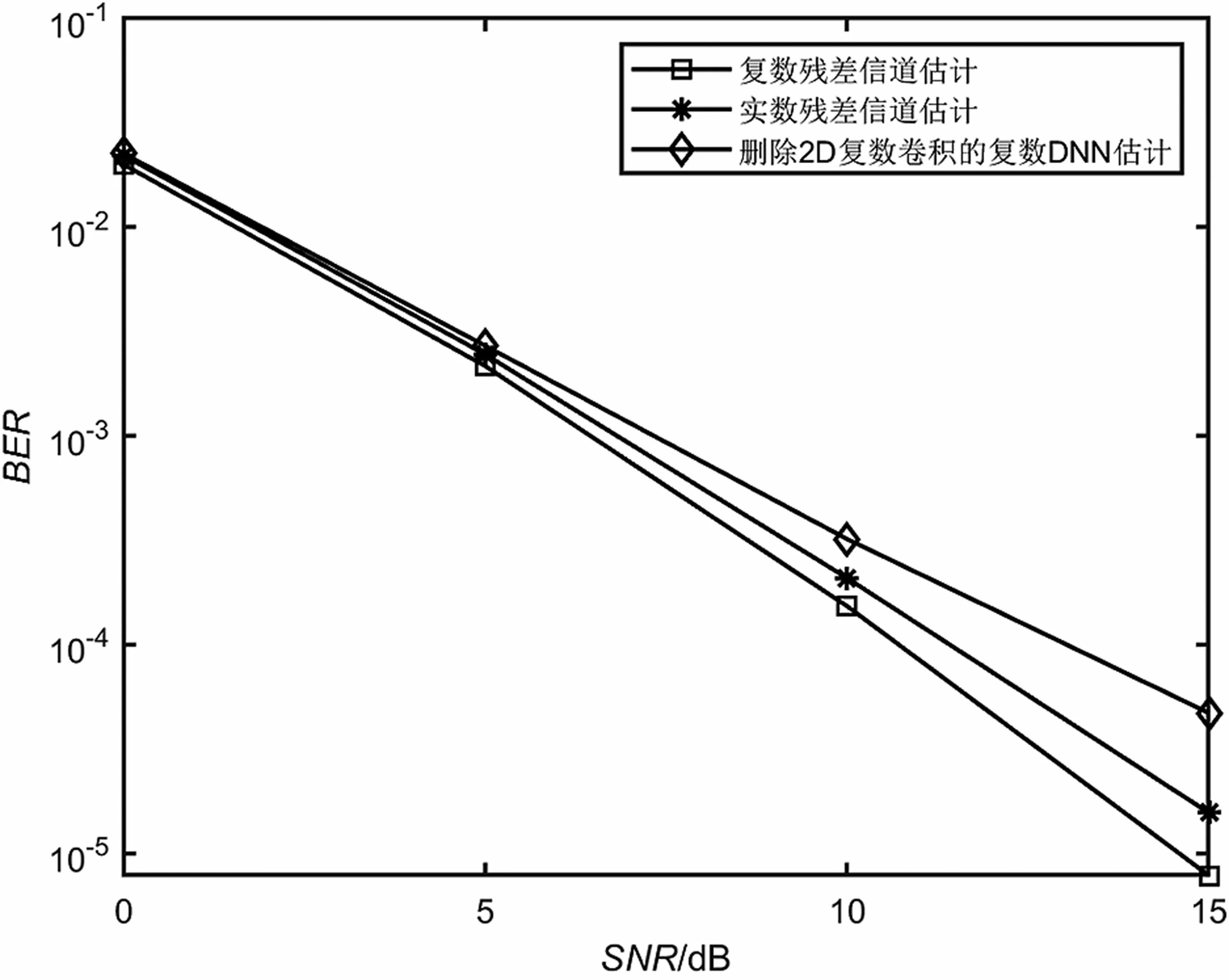
图8 本文方法与其他简化方法BER性能对比

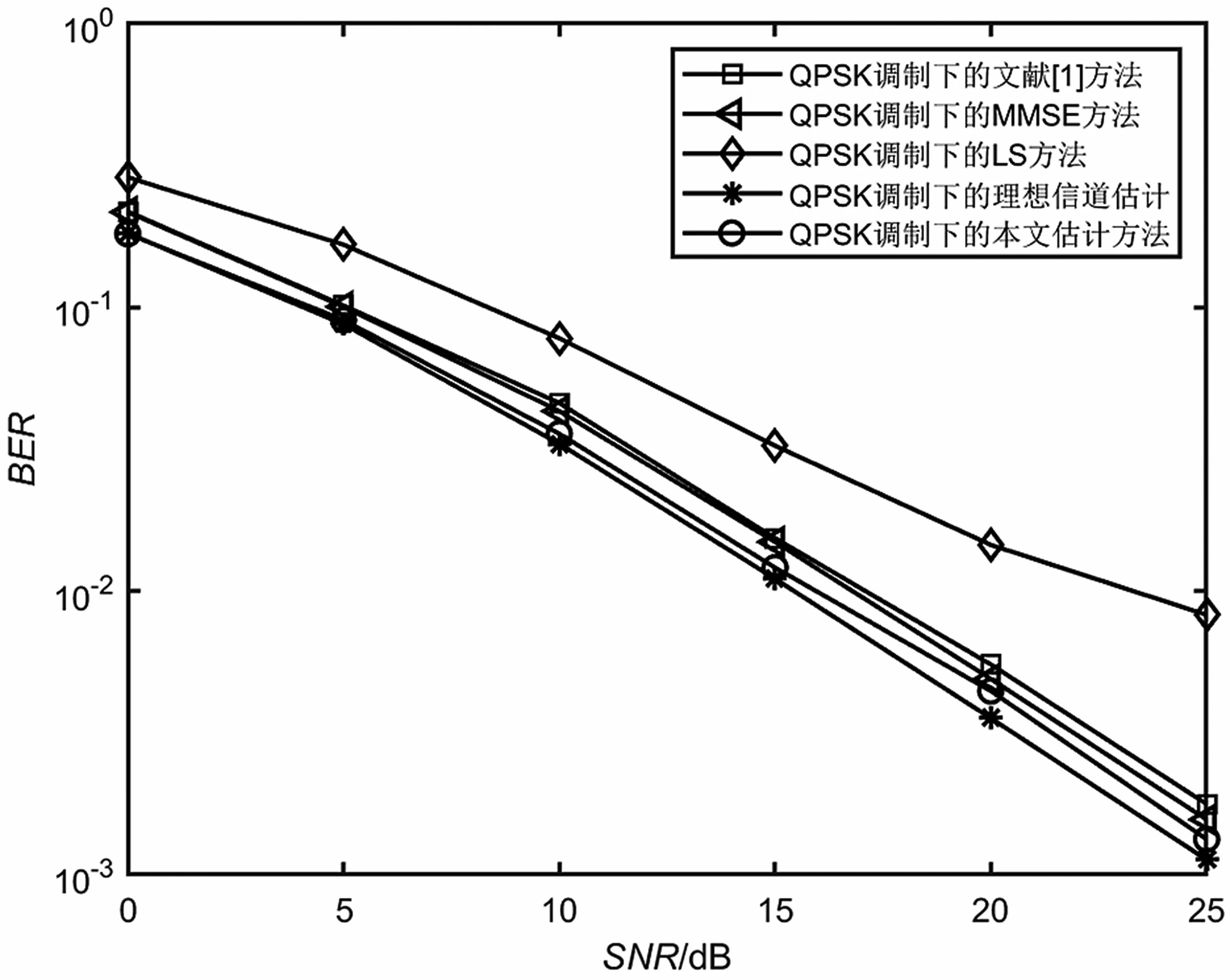
图9 各种估计方法BER性能对比

3.3 计算复杂度分析

如表3所示，理想的LMMSE信道估计算法的计算复杂度最高，去除CP的Cv-ReEsNet的计算复杂度次之。这表明Cv-ReEsNet较传统方法在训练过程中在不显著提高复杂度情况下能改善性能。

表3 算法的计算复杂度对比

4 结语

本文提出了一种卷积神经信道估计网络，用于从系统中恢复未编码比特。输入复数信号利用残差网络实现信道估计，同时用卷积神经网络代替DFT/IDFT转换波形。结果表明，本文算法误码率性能优于LMMSE等传统接收器，并且优于数据驱动和实数深度学习方法。此外，所提网络还证明了复数神经网络处理OFDM家族波形的能力。