车轮多边形激励下的滚动接触疲劳裂纹瞬态扩展行为研究*

2022-06-11张笃超黄双超温泽峰金学松

润滑与密封 2022年5期

张笃超赵鑫黄双超温泽峰金学松李伟

(西南交通大学牵引动力国家重点实验室四川成都 610031)

轮轨滚动接触疲劳是一种常见的轮轨损伤，是轨道交通领域持续关注的热点问题之一。一般认为滚动接触疲劳是循环载荷作用下材料塑性变形逐渐累积并超过其延展极限的后果，由高速移动的法向、切向接触载荷共同决定，且其发展与轮轨廓形演化紧密相关[1-2]。图1展示了我国某城际线路上发生的连续型钢轨滚动接触疲劳裂纹[1]。多裂纹情况下，容易发生裂纹相互贯穿，继而造成表层材料剥离掉块，恶化轮轨间相互作用；极少数情况下，钢轨裂纹会持续向下发展，最终或导致断轨[1,3]，威胁行车安全。

图1 某城际线路上出现的连续型钢轨滚动接触疲劳裂纹[1]

滚动接触疲劳发生在接触表层和次表层，相关材料受到复杂的三维接触应力，使得其裂纹萌生与扩展研究非常困难。针对滚动接触疲劳裂纹的扩展，国内外学者已做了大量研究，但是多为二维分析，且隐含了静态或稳态假设，常用移动载荷法来模拟接触载荷，即忽略了轮轨瞬态滚动接触行为及其之间的高频动力作用。FLETCHER等[4]采用边界元法，建立了多条钢轨滚动接触疲劳裂纹的二维扩展模型，通过计算裂尖应力场强度因子，评判了裂纹间的相互影响。OLZAK等[5]建立了二维准静态有限元模型，分析了滚动接触过程中单条斜裂纹应力状态分布及裂尖应力场强度因子随时间的变化。GOSHIMA和KEER[6]建立二维滚动接触疲劳斜裂纹的解析模型，利用复变技术求解积分方程，研究了摩擦热对裂尖应力场强度因子的影响。李伟等人[7]利用有限元法模拟了热机耦合下的多裂纹二维模型，考虑了摩擦温升对材料本构的影响，分析了裂纹间相互作用和裂纹数量对裂纹扩展行为的影响。曹世豪等[8]基于二维有限元斜裂纹模型，研究了裂纹由0.1 mm深扩展到2 mm深时的规律，指出初期裂纹扩展由张开型扩展主导，之后逐渐转变为滑开型主导，达到0.3～0.5 mm波深后，裂纹倾向于向钢轨表面扩展，并最终导致剥离掉块。杨鸿达等[9]建立了二维单条斜裂纹的有限元模型，并在主裂纹尖端虚设了不同角度的次裂纹，用来计算斜裂纹扩展路径，预测的扩展方向与实际观测相符合。汪鹏鹏等[10]在单条斜裂纹扩展有限元模型的基础上，通过雷诺方程计算了侵入液体时裂纹面上压力，分析了移动赫兹载荷通过钢轨裂纹时，不同黏度液体对裂纹扩展角度和速率的影响。

为研究钢轨滚动接触疲劳裂纹的动态扩展行为，ZHAO等[11]建立了包含轮轨瞬态滚动接触行为模拟的三维平面裂纹瞬态扩展模型，裂尖三向应力场强度因子由虚拟裂纹闭合法[12-13]来计算。该模型为时域内分析模型，最高模拟速度500 km/h，可精确模拟牵引、制动、曲线通过等不同工况下，接触斑经过裂纹时的法向、切向接触载荷瞬变过程，考虑了多轴接触应力场、材料应变率效应、第三介质等因素。利用上述模型，赵小罡等[14]分析了黏着系数对裂纹扩展的影响，王喆等人[15]分析了多裂纹之间的相互影响及裂纹临界间距。

以上研究均未分析车轮多边形的影响，而车轮多边形作为一种短波几何不平顺，极大地恶化了轮轨间的接触关系，使得高速运行的车轮产生高频受迫振动，增大了轮轨接触力和接触应力的高频和瞬态效应[16-17]，进而改变了接触表面裂纹的载荷边界条件，不可避免地影响裂纹扩展行为。

本文作者建立考虑带车轮多边形的三维钢轨裂纹瞬态扩展分析模型，分析车轮多边形对多裂纹扩展行为的影响。

1 模型建立

1.1 三维轮轨滚动接触疲劳裂纹扩展模型

图2所示是基于ANSYS/LS-DYNA建立的三维轮轨滚动接触疲劳裂纹扩展模型。鉴于我国高速铁路以直线和大半径曲线为主[18]，所以只模拟了直线段轨道。模型从上到下依次为簧上质量、一系悬挂、车轮、钢轨、扣件、轨道板和砂浆层，考虑其结构对称性，模型只考虑1/2轮对和轨道，忽略轮对横移，以降低模型规模。由于多边形激励下轮轨间动力作用属于高频范畴，而车辆-轨道耦合系统的高频响应主要由轮对和轨道的柔性决定，因此一系悬挂以上的所有部件简化为刚体并通过一系悬挂与车轴相连[19]。总轨道长14.43 m，车轮型面采用S1002CN型，钢轨型面采用CN60型，轨底坡1∶40。以初始位置为原点O，建立如图2所示的笛卡尔坐标系Oxyz。模型的主要计算参数见表1,材料参数见表2。

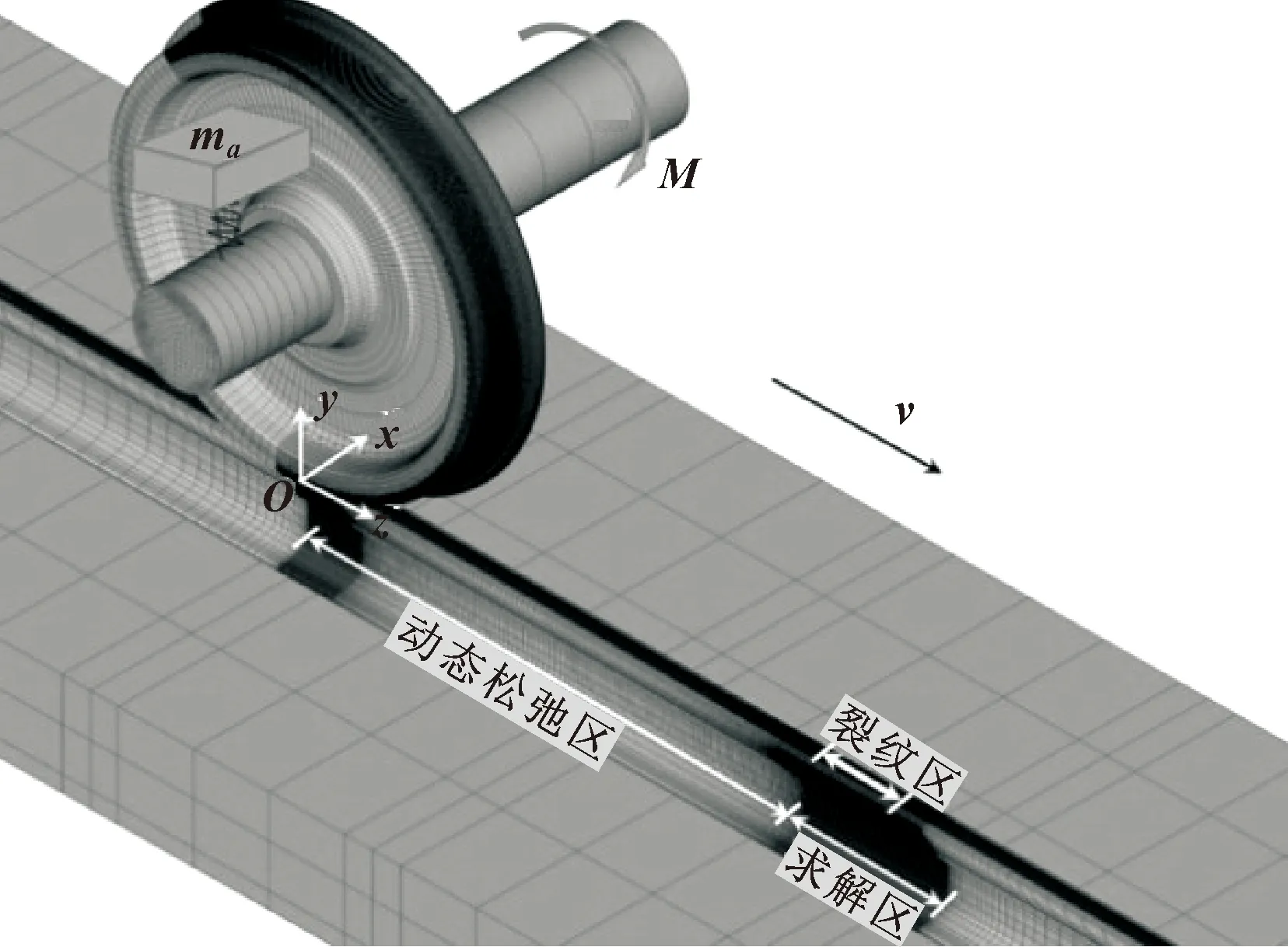
图2 三维轮轨滚动接触疲劳裂纹有限元模型

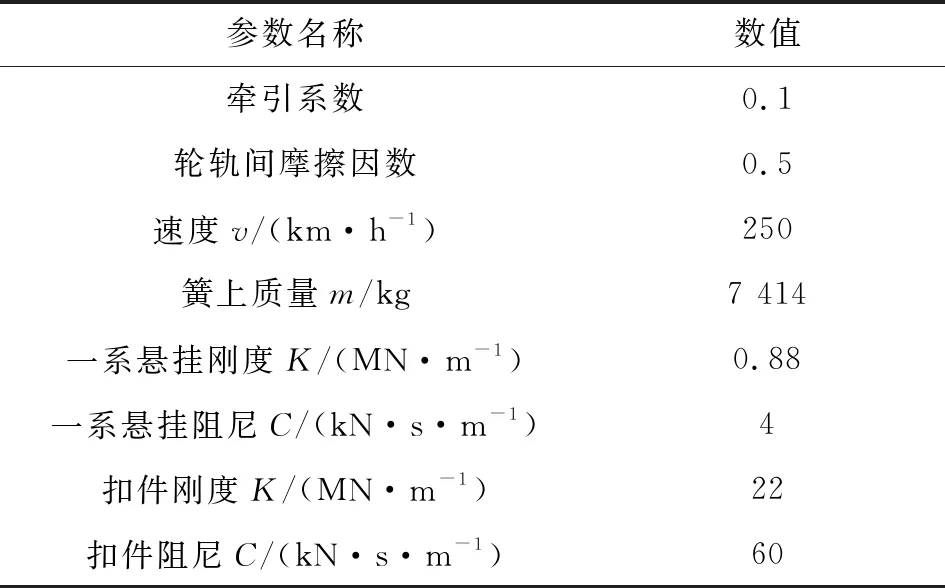
表1 模型计算参数

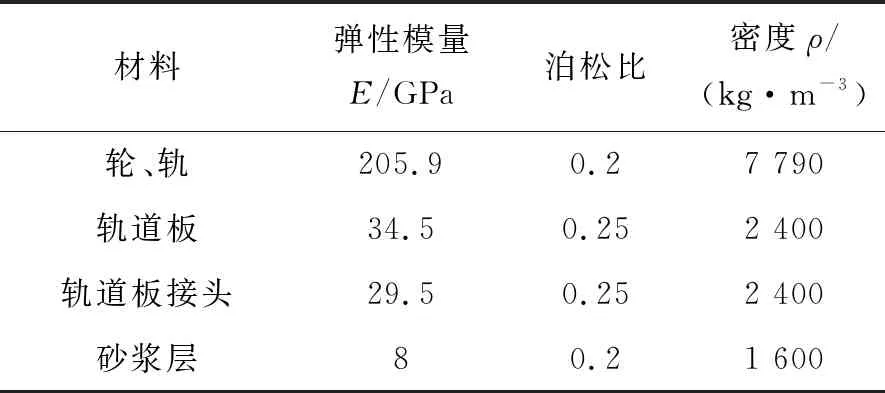
表2 材料参数

钢轨裂纹置于图2中纵向长0.33 m的求解区，之前的动态松弛区，旨在保证车轮在滚入求解区时，达到近似稳态滚动状态[19]。求解区内施加裂纹的区域，进一步称为裂纹区。为保证求解精度和降低模型规模，采用非均匀网格进行离散，求解区内采用细密网格，最小网格尺寸0.25 mm，其他区域，尤其是非接触表面，采用尽可能大的网格。模型总单元和节点数量分别为210万和228万。

为应对网格过渡难题，求解区纵向两端采用了非连续网格，边界左侧的动态松弛区最小网格为1 mm，而求解区内0.25 mm。非连续边界面上设置了摩擦因数设为100的“面-面”接触，来近似模拟连续材料。考虑此边界影响，裂纹区边界设在非连续边界内90 mm处，如图3所示。根据现场裂纹实际观测[20-27]，多裂纹均假设为半椭圆形裂纹面，其特征长度l=15 mm，深度h=3 mm，倾斜角度30°，裂纹间距d=5 mm，且假设所有裂纹相同，具体施加位置及尺寸也示于图3。共施加31条裂纹，即裂纹区总长150 mm。

图3 裂纹施加位置及尺寸

裂纹通过复制节点的方法来施加，即由离散完的模型中选取裂纹面内节点，复制出位置完全相同的一组节点构成另一裂纹面，裂纹面内节点和裂纹面外节点交界的地方即为裂尖，2个裂纹面之间设置“面-面”接触，即模拟了零间隙裂纹。图4给出了一条裂纹面内节点位置在xy平面的投影，黑线为裂尖。为描述裂尖位置，以裂纹表面中心为原点，建立如图4所示的极坐标系O′rθ。以往的研究表明，液体侵入导致的裂纹面间低摩擦因数会促进裂纹的扩展[11]，因此所有裂纹的两裂纹面间摩擦因数设为0，模拟最恶劣工况。裂尖应力场强度因子，由虚拟裂纹闭合法计算，具体公式及验证见文献[14-15]。

图4 某一裂纹面节点在x-y平面投影

1.2 多边形的施加

车轮多边形是指车轮踏面周向不均匀磨损导致的车轮非圆化，我国高速列车大量出现了高阶多边形现象[28]。文中考虑文献[28]中报道的某城际动车组出现的23阶车轮多边形，并将多边形抽象为23阶简谐波，波深取实测典型值0.1 mm，宽度取足够宽的40 mm(假设深度在横向上呈抛物线分布)，见图5。具体施加车轮多边形时，通过修改车轮表面相关节点坐标的方式来实现。多边形施加范围从距离初始接触位置(车轮最下部)45°处开始，至对应钢轨求解区末端的位置结束，防止恶化模型的初始条件设置和动态松弛效果。

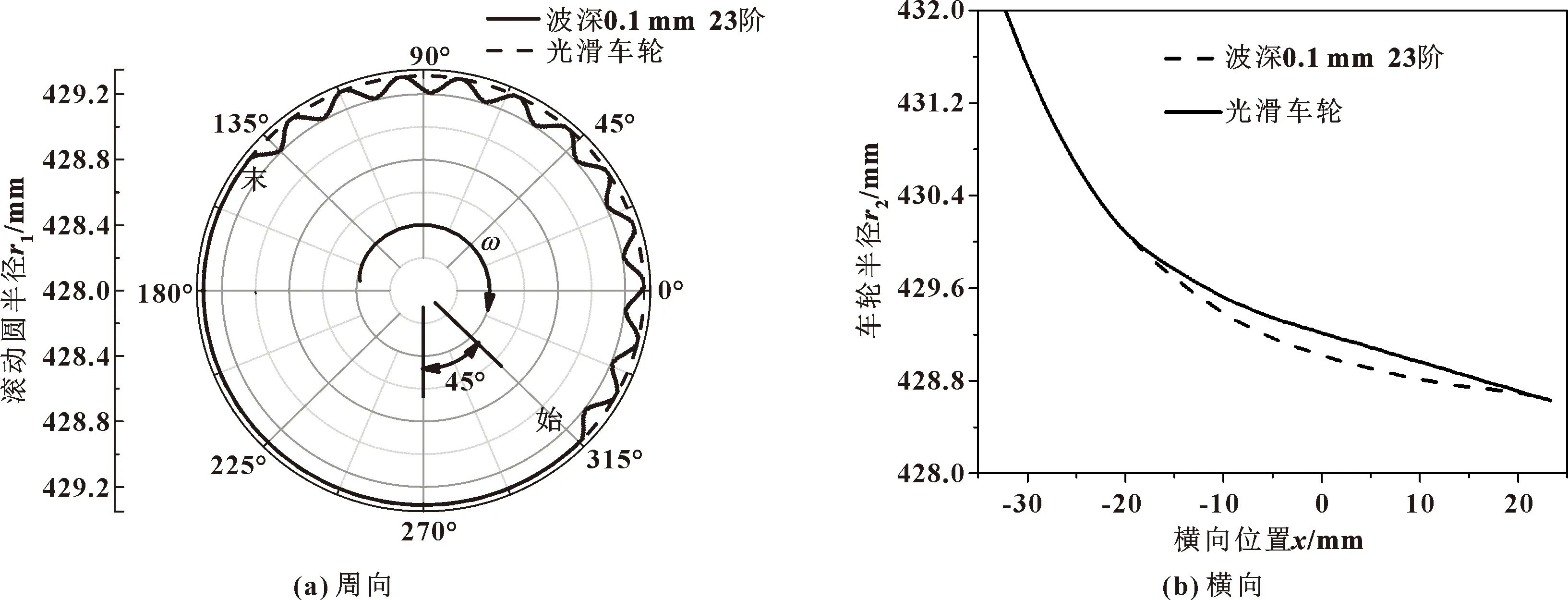
图5 施加的车轮多边形几何示意

2 模拟结果及分析

2.1 轮轨接触力

仅钢轨裂纹、仅车轮多边形及钢轨裂纹和车轮多边形同时存在等3种工况的轮轨力计算结果如图6所示，具体为原始轮轨力结果与无缺陷工况(无裂纹和多边形)相应结果之差，即所示结果为裂纹和多边形造成的轮轨力波动。

图6 裂纹和多边形引起的轮轨力波动

可见，31条零间隙裂纹对法向轮轨力的影响可以忽略，但会使切向轮轨力产生幅值达到2.02 kN的波动。导致这样的原因是车轮驶入裂纹区时，钢轨材料从连续变为不连续，对轮轨相互作用而言，实质上引入了一种激励作用，而法向轮轨力的绝对值远大于切向，且忽略了裂纹面间的间隙，使得裂纹对法向轮轨力的影响可以忽略，但裂纹面间的零摩擦因数等因素，使得切向轮轨力产生了不可忽略的波动。0.1 mm波深的23阶多边形会造成法向、切向轮轨力的显著波动，在裂纹区内的最大幅值分别为28.3和1.88 kN。所以，当裂纹和多边形同时存在时，法向轮轨力不受裂纹的影响，与仅多边形工况基本一致，而切向力受到裂纹的激励，波动幅值更大，达3.64 kN。

2.2 裂纹面接触力

图7展示了圆顺和带0.1 mm波深23阶多边形车轮滚过裂纹区过程中，各条裂纹的裂纹面所承受的最大法向、切向接触力，横坐标为裂纹编号(裂纹从左到右依次编号，也代表了各裂纹在钢轨上的纵向位置)。可以看出，在圆顺车轮工况下各裂纹面的法向、切向裂纹面最大接触力基本相同，分别稳定在11.9和0.041 kN，说明车轮处于近似稳态滚动状态；引入车轮多边形后，各裂纹的状态呈明显波动，最大法向、切向裂纹面最大接触力分别达14.3和0.055 kN，比上述稳态值分别高了19.6%和34.1%，具体发生位置在多边形几何的上升段。

图7 裂纹编号及各裂纹面最大接触力

以裂纹面接触力最大的裂纹16 (见图7)为例，选取了图8所示的5个时刻(t1～t5)来展示裂纹面上应力分布的瞬态变化，见图9和10。其中，t1时刻接触斑前沿抵达裂纹16，t3时刻接触斑中心抵达裂纹16，t5时刻接触斑后延刚好离开裂纹16。由图9所示裂纹面内法向接触应力云图可见，法向接触应力在t3时刻达到最大；就空间分布而言，最大值发生在约0.62 mm波深处，更靠近钢轨外侧；t1～t3时刻，带多边形工况的结果明显大于圆顺车轮工况，以t3时刻为例，高了7.3%；而在t4～t5时刻，却是圆顺工况下更高，对应图6和7中的动力减载段(即载荷低于静载)。

图8 5个不同时刻下接触斑位置示意

图9 不同时刻下裂纹16裂纹面内法向接触应力分布云图

图10展示的是裂纹16裂纹面内切向接触应力的矢量分布，箭头尾部为节点位置，箭头方向代表节点处的切向接触应力方向，箭头的长度则代表应力的幅值。可以看出，带多边形激励的5个时刻切向接触应力幅值均大于圆顺车轮工况；多边形激励下，切向接触应力也是在t3时刻达到最大，但其方向存在突变，t1、t2时刻大致向上，大约在t3时刻开始转为大致向下，这是由于轮轨接触载荷的施力位置在此时刻由裂纹左侧移至右侧所致。

图10 不同时刻下裂纹16裂纹面内切向接触应力矢量分布

2.3 裂尖应力场强度因子

2.3.1 裂纹间差异

裂纹16位于裂纹区中间，受到裂纹区边界的影响最小，图11给出了其在圆顺车轮整个滚动过程中裂尖各处所承受的最大应力场强度因子。可以看出，KII的最大值出现在6.03 rad处,KIII的最大值出现在3.92 rad处；KII的最大值是KIII最大值的2.24倍。这意味着裂纹如果能扩展，外侧裂尖应该以II型扩展为主，而内侧(轨距角侧)裂尖以III型为主。计算结果表明该裂纹并未发生I型扩展，原因是钢轨受到垂向载荷的作用，发生垂向弯曲变形，使2个裂纹面始终处于紧密贴合、相互挤压状态[30]，故图中只给出KII和KIII(后文其他结果亦如此)。

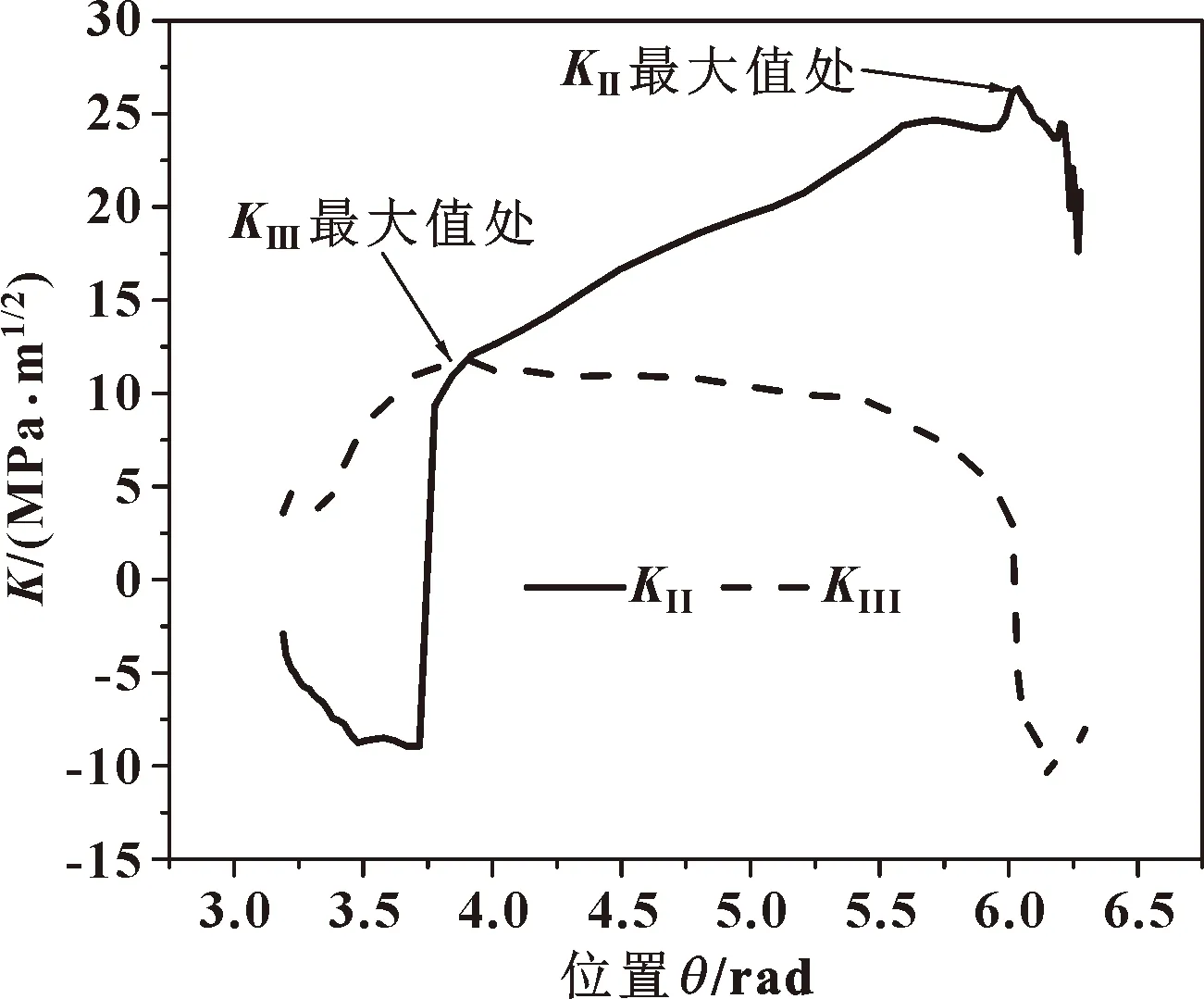
图11 圆顺车轮下裂纹16裂尖的最大应力场强度因子分布

选取每条裂纹裂尖上的KII和KIII最大值发生位置，图12展示了圆顺车轮滚过31条裂纹(从左往右依次示出)时该选取位置上K因子的时变特性曲线，横坐标纵向距离代表轮心在不同时刻下的滚动距离。

图12 圆顺车轮下31条裂纹裂尖应力场强度因子的时变特性曲线

从图12(a)中可以看出，中间29条裂纹的KII时变特性基本一致(峰值最大差别仅0.43%)，裂纹1和31的幅度分别低了12.5%和11.7%。原因是当车轮驶入和驶出裂纹区时都会导致轮轨接触状态突变，而在裂纹区以内(中间29条裂纹)达到近似“稳态”。这与文献[15]中得出的3条裂纹可以捕捉到多裂纹间相互影响的结论一致。从图12(b)中可以看出，KIII的最大值在各裂纹间存在较明显的小幅波动，使得裂纹1和31的特殊性大大降低，并无像KII一样的差异，原因是KIII主要受横向力主导，而文中分析忽略了轮对横向运动，即横向轮轨力近似为0，这对应着高速列车运行时的高平稳性。

2.3.2 车轮多边形影响

图13对比展示了圆顺和带0.1 mm波深23阶多边形车轮分别滚过裂纹区过程中，各裂纹裂尖6.03 rad处的最大KII值和3.92 rad处的最大KIII值。考虑到裂纹1和31的特殊性(见2.3.1小节)，分析中忽略掉它们的相应结果，24条裂纹(例如4～27)刚好对应一个多边形波长(117 mm)。

图13 波深0.1 mm的23阶多边形对裂尖应力场强度因子的影响

从图13可以看出，车轮多边形的存在，使得最大裂尖强度因子呈现出与多边形周期对应的周期性波动，且KII和KIII大致同相位波动，均超前于多边形几何约60°。另外较圆顺车轮工况而言：KII、KIII的波动并未围绕其作等幅波动，而是正向波动幅度远小于负向波动。这主要是因为多边形工况下的接触载荷边界(即轮轨力)并非在静态值上下呈等幅波动。与圆顺工况相比，一个周期内KII波峰和波谷处的变化量分别为4.2%和-18.9%，而KIII峰、谷处变化量分别为7.9%和-20.4%。需指出，若裂纹区足够长，也会存在增加值大于减小值的区域。进一步考虑到裂纹扩展速率并不是与K因子线性相关，所以车轮多边形会加速钢轨滚动接触疲劳裂纹的扩展。

2.3.3 多边形波长与波深影响

我国高速列车车轮多边形的现场观测表明，其阶数和深度会随不同线路、运营速度、车型及车轮服役运营里程等变化[28]。因此，有必要研究车轮多边形阶数和深度对裂纹扩展的影响。

保持2.3.2小节中的23阶多边形不变，改变其波深在0.05～0.35 mm范围内变化，分析一个周期内各裂纹最大裂尖应力场强度因子波动范围。跟图13一样，选取裂尖6.03、3.92 rad处的KII、KIII结果，得到的变化范围对比结果见图14(周期定为裂纹4～27，见图13)。

图中的实心符号代表圆顺车轮工况下该选定周期范围内裂纹K因子的平均值，上限和下限代表带多边形时选定周期内K因子波动的峰值和谷值(对应图13中的峰、谷值)。从图14可以看出，随着波深的增加，KII、KIII的波动幅度变大，但是峰值增加幅度始终小于谷值的降低幅度。例如，当波深达到0.35 mm时，KII、KIII值的峰值较圆顺工况平均值分别增加15.8%、26.4%，而谷值分别降低了113.5%和135.9%。

阶数变化时，考虑到低阶多边形其波长较大，例如8阶对应337 mm，16阶168.5 mm，大于模型中的裂纹区长度150 mm。这意味着模型不能完整反映一个多边形周期内的KII、KIII波动情况。进一步考虑到多边形造成裂尖强度因子增加的危害更大，在施加低阶多边形时，保证能捕捉到多边形导致的裂尖强度因子增加峰值。图15展示了不同阶数多边形造成的裂尖强度因子增加峰值对比，考虑的多边形阶数上下限分别为8和40阶，波深保持0.1 mm不变，KII、KIII结果同样取自裂尖6.03和3.92 rad处，0阶对应着圆顺车轮工况。从图15可以看出，随着阶数的增加，KII、KIII的增加峰值增大，达到40阶时，KII、KIII增加峰值相较于圆顺工况分别增加15.9%和17.7%。