基于旋转模型的数学压轴题研究

苏国东

[摘 要]图形旋转是初中数学的难点，基于旋转模型的数学压轴题是试题研究的热点。文章以三道基于旋转模型命制的数学压轴题为例，指出其图形构成与命制方式体现了立足教材、渗透模型、发展能力等特点，以及教师在教学中要挖掘试题的教育价值，发挥试题的应用价值。

[关键词]旋转模型;压轴题;研究

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2022）08-0004-03

图形的旋转是初中数学的重难点，其与三角形、四边形、圆等几何模块知识都有着密切联系，旋转模型更是各类数学试题的考查热点，亦是试题研究者的关注点。本文以三道基于旋转模型命制的数学压轴题为例，对其图形构成与命制方式进行研究。

一、核心概念界定

（一）旋转模型

在等腰三角形（包括等边三角形、等腰直角三角形）、正方形等具备“等线段、共顶点”特征的图形背景下，通常可以进行旋转变换解题。根据形式不同，可归结为几类常见的旋转模型，如“手拉手”模型、“夹半角”模型和“对角互补”模型。

（二）数学压轴题

所谓数学压轴题，一般是指数学试卷中选择题和填空题的最后一题，以及解答题的最后两题，多数为几何或函数综合题。数学压轴题具有知识点多、覆盖面广、条件隐蔽、解法灵活等特点，集中体现了知识方法的综合以及能力的立意。

二、试题研究

（一）“手拉手”模型

“手拉手”模型，是指由两个共顶点且顶角相等的等腰三角形（或等边三角形）组成的图形。在人教版教材八年级上册第83页习题第12题、九年级上册第63页习题第10题均有提及。

如图1，在等腰[△BAD]和[△CAE]中，[∠BAD=∠CAE]，连接[DC]，[BE]，则有[△DAC≌△BAE]（记为结论1，下同）、[DC=BE]（结论2）、[DC]与[BE]的夹角等于[∠BAD]（结论3）。

如图2是常见的“三点共线”的等腰直角三角形“手拉手”模型，其中[△ABD]和[△AGE]为等腰直角三角形。以斜边[BD]，[GE]为对角线向外翻折得到如图3所示的正方形“手拉手”模型。

[例1]（1）如图3，四边形[ABCD]和[AEFG]都是正方形，点[E]在边[AB]上，连接[BG]和[DE]，则线段[BG]与[DE]有何数量关系和位置关系？

（2）如图4，将图3中正方形[AEFG]绕点[A]逆时针旋转一定的角度，则（1）中的结论是否还成立？请说明理由。

（3）如图5，直线[l]上有两个动点[A]，[B]，直线[l]外有一点[O]，连接[OA]，[OB]，[OA=2]，[OB=2]，以线段[AB]为边在[l]的另一侧作正方形[ABCD]，连接[OD]。在动点[A]，[B]运动的过程中，线段[OD]的长是否存在最大值？若存在，求出这个最大值;若不存在，请说明理由。

点评：本题直接使用了图3作为题图，考查正方形“手拉手”模型中的常规结论与推广。第（1）問和第（2）问由“手拉手”模型可知△[BAG≌△DAE]（结论1）、[BG=DE]（结论2）、[BG]与[DE]互相垂直（结论3）;第（3）问需要类比联想，构造“手拉手”模型。如图6，以[OA]为边作正方形[OAGF]，连接[OG]，[BG]，则[OG=2OA=2]，由（2）的结论有[OD=BG]，所以当[G]，[O]，[B]三点共线时[BG]最长，此时[BG=OG+OB=2+2=4]，故线段[OD]的长存在最大值4。

（二）“夹半角”模型

“夹半角”模型的特点是在一个已知的大角（一般为90°或120°）中含有这个大角一半的一个小角，可以通过旋转构造等角，从而得到全等三角形。

如图7，在正方形[ABCD]中，[∠EDF=45°]，因为[AD=DC]且共顶点[D]，所以可将[△ADE]绕点[D]逆时针旋转90°得到[△CDK]，[K]，[C]，[B]三点共线，可证明[△EDF≌△KDF]、[EF=KF=AE+CF]（结论1）、[△EBF]的周长等于正方形边长的2倍（结论2）等。

此外，人教版教材八年级下册第69页习题第14题给出了以下结论：如图8，四边形[ABCD]是正方形，点[E]是边[AB]的中点，[∠DEG=90°]，[EG]交正方形外角的平分线[BG]于点[G]，则有[DE=EG]（结论3），当点[E]不是[AB]中点时结论仍然成立。方法是在[AD]上截取[AH=AE]，连接[HE]，证明[△DHE≌△EBG]即可。

将图7与图8的[E]点及正方形各顶点对应字母重叠，即巧妙构造出了图9。

[例2]如图9，在边长为1的正方形[ABCD]中，点[H]，[E]分别是边[AD]，[AB]上的两个动点（与点[D]、[A]、[B]不重合），[AH=AE]，[DE⊥EG]，[EG]交正方形外角的平分线[BG]于点[G]，[DG]交[BC]于点[F]，连接[HE]，[EF]。

（1）求证：[△DHE≌△EBG];

（2）求[∠EDG]的度数;

（3）设[AE=x]，当[x]为何值时，[EF∥BG]，并求出此时[△DEF]的面积。

点评：由图形的构造方式可知，尽管已知条件有所改变，但利用图7、图8的解题思想可迅速找到本题的突破口。第（1）问和第（2）问中，易证[△DHE≌] [△EBG]，[DE=EG]（结论3），因为[DE⊥EG]，所以[∠EDG=45°];第（3）问中，将[△ADE]绕点[D]逆时针旋转90°得到[△CDK]，如图9。由“夹半角”模型有[EF=KF]（结论1），再根据[EF∥BG]得出[∠FEB=45°]，所以[EB=BF]。因为[AE=KC=x]，所以[EB=BF=1-x]，[CF=x]，[EF=KF=2x]。在[Rt△EBF]中，由勾股定理有[（1-x）2+（1-x）2=（2x）2]，解得[x=2-1]，所以[S△DEF=S△DKF=12×2×2-1×1=2-1]。2D53453F-AB58-405C-94D1-B69E72447833

（三）“对角互补”模型

“对角互补”模型，即在四边形或其构成的几何图形中，相对的角互补，特殊的情况主要有含90°和60°两种。

以含90°的情况为例，如图10，四边形[ABCD]中，[∠BAD=∠BCD=90°]，所以[∠ABC+∠ADC=180°]。当给出条件[AB=AD]时，可将[△ADC]绕点[A]顺时针旋转90°得到[△ABE]，再证明[△AEC]为等腰直角三角形;当给出条件[CA]平分[∠BCD]时，可作[AE]垂直[AC]交[CB]的延长线于点[E]，再证明[△AEC]为等腰直角三角形，所以有[2AC=EC=BC+CD]（结论1）、[S四边形ABCD=S△AEC]（结论2）。

含60°的情况类似，以例3为例进一步说明和应用。

[例3]（1）如图11，[△ABC]是等边三角形，[∠ADC=120°]，连接[BD]，试探究线段[DA]，[DB]，[DC]之间的數量关系，并说明理由;

（2）如图12，在四边形[ABCD]中，[∠A+∠C=180°]，[DA=DC]，过点[D]作[DE⊥BC]于点[E]，探究线段[AB]，[BC]，[CE]之间的数量关系，并说明理由。

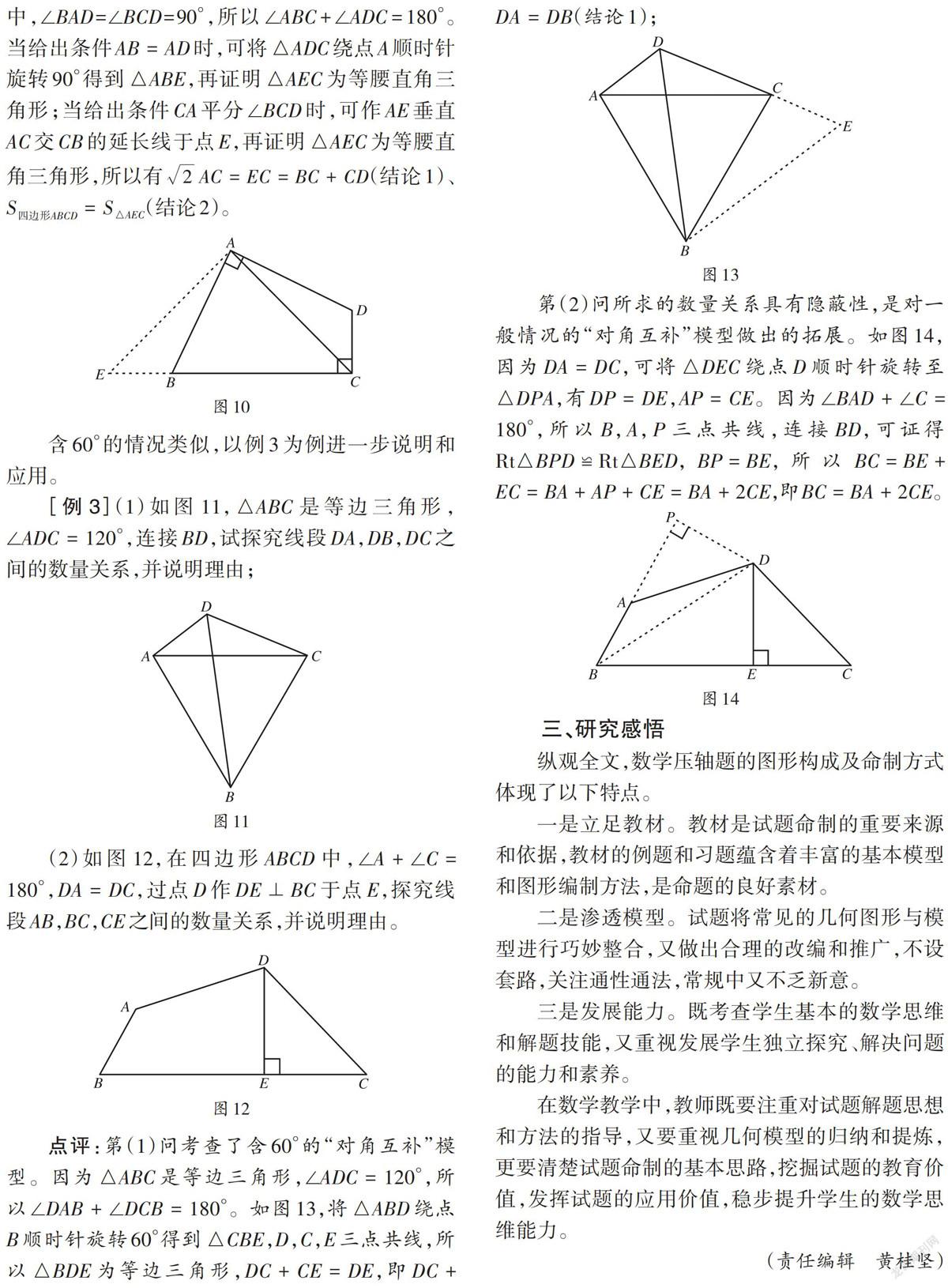
点评：第（1）问考查了含60°的“对角互补”模型。因为[△ABC]是等边三角形，[∠ADC=120°]，所以[∠DAB+∠DCB=180°]。如图13，将[△ABD]绕点[B]顺时针旋转60°得到[△CBE]，[D]，[C]，[E]三点共线，所以[△BDE]为等边三角形，[DC+CE=DE]，即[DC+DA=DB]（结论1）;

第（2）问所求的数量关系具有隐蔽性，是对一般情况的“对角互补”模型做出的拓展。如图14，因为[DA=DC]，可将[△DEC]绕点[D]顺时针旋转至[△DPA]，有[DP=DE]，[AP=CE]。因为[∠BAD+∠C=180°]，所以[B]，[A]，[P]三点共线，连接[BD]，可证得[Rt△BPD≌Rt△BED]，[BP=BE]，所以[BC=BE+EC=BA+AP+CE=BA+2CE]，即[BC=BA+2CE]。

三、研究感悟

纵观全文，数学压轴题的图形构成及命制方式体现了以下特点。

一是立足教材。教材是试题命制的重要来源和依据，教材的例题和习题蕴含着丰富的基本模型和图形编制方法，是命题的良好素材。

二是渗透模型。试题将常见的几何图形与模型进行巧妙整合，又做出合理的改编和推广，不设套路，关注通性通法，常规中又不乏新意。

三是发展能力。既考查学生基本的数学思维和解题技能，又重视发展学生独立探究、解决问题的能力和素养。

在数学教学中，教师既要注重对试题解题思想和方法的指导，又要重视几何模型的归纳和提炼，更要清楚试题命制的基本思路，挖掘试题的教育价值，发挥试题的应用价值，稳步提升学生的数学思维能力。

（责任编辑 黄桂坚）2D53453F-AB58-405C-94D1-B69E72447833