单位凯莱图及其补图的(无符号)拉普拉斯能量

袁雨晴

(兰州交通大学数理学院 甘肃 兰州 730070)

0 引言与预备知识

本文所考虑的图均为简单图。设图G的顶点集V(G)={v1,v2,…vn}，边集E(G)={e1,e2,…,em}。图G的补图G定义如下：G的顶点集与G的顶点集相同，G中任意两个顶点相邻当且仅当它们在G中不相邻。图G的度对角矩阵[1]D(G)=diag(d1,d2,…,dn)，其中di(1≤i≤n)为顶点vi的度。图G的邻接矩阵[1]A(G)=(aij)n×n定义如下：若顶点vi与顶点vj相邻，则aij=1；否则aij=0。图G的特征值[2]是指邻接矩阵A(G)的特征值。

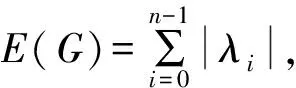
定义1[6]设Γ是具有单位元1的乘群，对任意S⊆Γ，1∉S，S-1={s-1|s∈S}=S，凯莱图X=Cay(Γ,S)是一个无向图。它的顶点集是V(X)=Γ，边集是E(X)={(a,b):a,b∈Zn,ab-1∈S}。

定义2[10]对任意正整数n>1，单位凯莱图Xn=Cay(Zn,Un)定义如下：顶点集V(Xn)=Zn，边集E(Xn)={(a,b):a,b∈Zn,a-b∈Un}。其中Zn是模n的剩余类加群{[0],[1],…,[n-1]}，Un={a∈Zn:gcd(a,n)=1}。

注2：单位凯莱图Xn是一个正则度为|Un|=φ(n)的正则图，其中φ(n)为欧拉函数[11]。

定义3[12]对任意正整数n>1，单位图Gn=Cay+(Zn,Un)是指以V(Gn)=Zn为顶点集，以E(Gn)={(a,b):a,b∈Zn,a+b∈Un}为边集的简单无向图。其中Zn是指模n的剩余类加群{[0],[1],…,[n-1]}，Un={a∈Zn:gcd(a,n)=1}。

注3：当n为偶数时,单位图Gn是|Un|=φ(n)-正则的；当n为奇数时，Gn是(φ(n),φ(n)-1)-半正则的[12]。

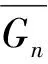
1 单位凯莱图及其补图的拉普拉斯能量

引理1[12]单位凯莱图Xn与单位图Gn同构当且仅当n为偶数。

引理3[14]当n为偶数时，单位图Gn=Cay+(Zn,Un)的拉普拉斯能量LE(Gn)=2rφ(n)，其中r是整除n的不同素因子的个数。

首先考虑单位凯莱图Xn的拉普拉斯能量。

证明 情形1当n为偶数时，结合引理1、3，容易看出，此时单位凯莱图Xn的拉普拉斯能量LE(Xn)=2rφ(n)，其中r是整除n的不同素因子的个数。

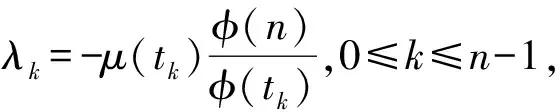
综上所述，单位凯莱图Xn的拉普拉斯能量LE(Xn)=2rφ(n)，其中r是整除n的不同素因子的个数。

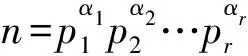
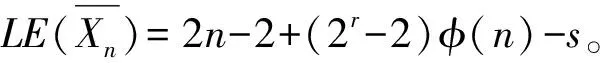
(2) 若p1≠2，即n为奇数，分成下面四种情形：

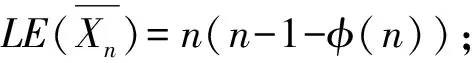
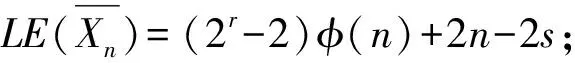
情形3：若n=s=p1p2…pr，则

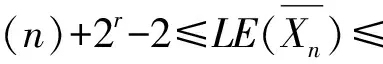
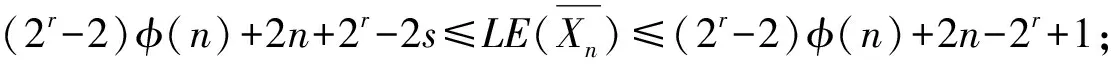
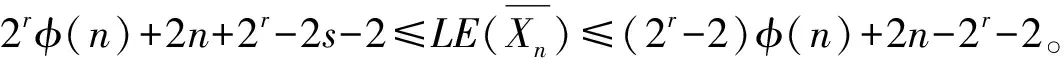
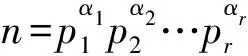
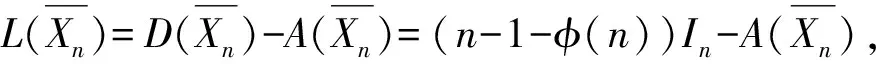
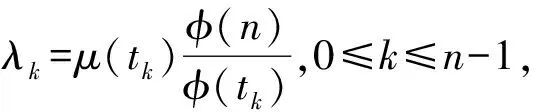
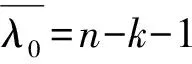
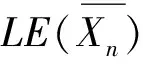
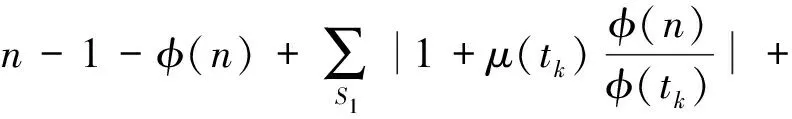
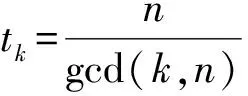
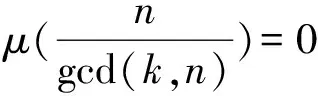
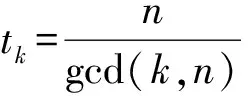
所以，

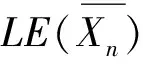
=(2r-2)φ(n)+2n-s-1+

因为每个tk分解式中包含的不同素数的个数是不一样的，下面分4种情形进行讨论。

情形2若n=pm且p≥3,m>1，有(n-s)=(n-p)个μ(tk)=0和(p-1)=(s-1)个μ(tk)=-1。其中k=tpm-1且t=1,2,3,…,p-1时，

则

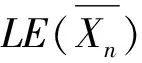
=(2r-2)φ(n)+2n-2s

情形3若n=s=p1p2…pr，有φ(n)个(k,n)=1，此时tk=n，μ(tr)=(-1)r。其余的n-1-φ(n)个k中不会出现μ(tk)=0的情况，但是无法确定μ(tk)=1或μ(tk)=-1的具体个数。因此有

情形3.1当r为奇数时，有

其余的n-1-φ(n)-(2r-1-1)-(2r-1-1)=n-φ(n)-2r+1个k中能使μ(tk)=1或μ(tk)=-1的个数不确定。因此有

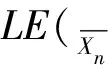
=(2r-2)φ(n)+2n-n-1+φ(n)×

(-1)+(n-φ(n)-2r+1)×(-1)

=(2r-2)φ(n)+2r-2

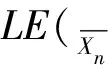
=(2r-2)φ(n)+2n-n-1+φ(n)×

(-1)+(n-φ(n)-2r+1)×1

=(2r-4)φ(n)+2n-2r

情形3.2当r为偶数时，有

其余的n-1-φ(n)-2r-1-(2r-1-2)=n-φ(n)-2r+1个k中能使μ(tk)=1或μ(tk)=-1的个数不确定。因此有

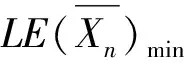
=(2r-2)φ(n)+2n-n-1+φ(n)×1+

(-1)×2+(n-φ(n)-2r+1)×(-1)

=2rφ(n)+2r-4

=(2r-2)φ(n)+2n-n-1+φ(n)×1-

2+(n-φ(n)-2r+1)×1

=(2r-2)φ(n)+2n-2r-2

也即：当r为奇数时，有

≤(2r-4)φ(n)+2n-2r

当r为偶数时，有

≤(2r-2)φ(n)+2n-2r-2

情形4.1当r为奇数时，有

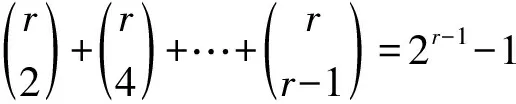
其余的s-1-2r-1-(2r-1-1)=s-2r个k中能使μ(tk)=1或μ(tk)=-1的个数不确定。因此有

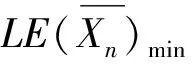
=(2r-2)φ(n)+2n-s-

1+1+(-1)×(s-2r)

=(2r-2)φ(n)+2n+2r-2s

=(2r-2)φ(n)+2n-s+1+

(s-2r)×1

=(2r-2)φ(n)+2n-2r+1

情形4.2当r为偶数时，有

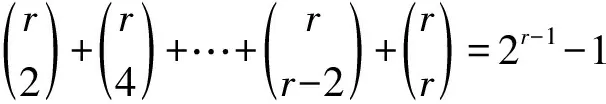
其余的s-1-2r-1-(2r-1-1)=s-2r个k中能使μ(tk)=1或μ(tk)=-1的个数不确定。因此有

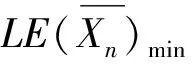
=(2r-2)φ(n)+2n-s-1+

(-1)+(s-2r)×(-1)

=(2r-2)φ(n)+2n+2r-2s-2

=(2r-2)φ(n)+2n-

s-1+(-1)+(s-2r)×1

=(2r-2)φ(n)+2n-2r-2

也即：当r为奇数时，有

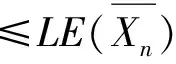
≤(2r-2)φ(n)+2n-2r+1

当r为偶数时，有

≤(2r-2)φ(n)+2n-2r-2

2 单位凯莱图及其补图的无符号拉普拉斯能量

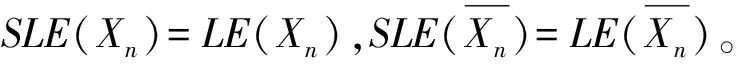
3 结语