再论光速不变原理和洛伦兹变换
2022-06-10余勇
余 勇
(江苏第二师范学院 物理与电子工程学院,江苏 南京 211200)
通过狭义相对论的两个基本假设,即相对性原理和光速不变原理可以推导出洛伦兹变换关系式. 作为狭义相对论最重要的关系式之一,有多种不同的方法推导洛伦兹变换关系[1-4],但是这些推导除了利用相对性原理和光速不变原理外,通常会用到做相对运动的两参考系的爱因斯坦条件[1,5],或者称之为运动的相对性条件,即如果惯性参考系S′以速度v相对惯性系S运动,那么反过来,S系必然以速度-v相对S′运动.很明显,经典的伽利略变换满足运动的相对性条件.但是在狭义相对论中,相对性原理指的是物理规律在所有的惯性参考系中都可以表示为相同的形式,并不包含爱因斯坦条件或运动的相对性条件,因此运动的相对性应该是洛伦兹变换的推论,而不是洛伦兹变换关系的前提条件.
另一方面,电动力学教科书一般利用间隔不变性来推导洛伦兹变换[6,7],但是光速不变原理与间隔不变性并没有显而易见的等价关系.事实上,电动力学教科书在论证间隔不变性时除了利用光速不变原理,也用到了运动的相对性条件[6].本文给出了洛伦兹关系式的一种简洁推导,一方面证明了通过相对性原理和光速不变原理可以推导出运动的相对性条件和洛伦兹变换关系,另一方面说明在相对性原理的假设下,光速不变原理、间隔不变性和洛伦兹变换关系三者是等价的.
1 二维时空洛伦兹变换与运动相对性条件
根据狭义相对性原理,两惯性参考系间坐标的变换为线性关系[6-8].为了简单起见,先考虑2维时空的情况.设惯性参考系S′以速度v相对惯性系S沿x轴正向运动.令初始时刻两坐标系的原点重合,即t=t′=0时,x=x′=0,变换关系为
x′=a11x+a12t,t′=a21x+a22t
(1)
在S系看来,S′系相对S系以速度v沿x轴方向运动.在S′系中任意时刻坐标原点O′的坐标为(0,t′),而在S系看来O′的坐标为(vt,t).将其代入式(1)可得:0=a11vt+a12t,因此有
a12=-va11
(2)
下面根据光速不变原理推导系数a21、a22和a11的关系.首先,设S系的坐标原点O在t=0时发出
一光束沿x轴正向传播,即x=ct
(3)
根据光速不变原理,在S′系中,有x′=ct′
(4)
把式(1)、式(2)代入式(4)得
a11x-va11t=c(a21x+a22t)
(5)
把式(3)代入式(5)可得
a11(c-v)=c2a21+ca22
(6)
同理,若S系的坐标原点O在t=0时发出沿x轴负向传播的一束光,根据光速不变原理有:x=-ct和x′=-ct′.与上面推导过程类似可得
a11(-c-v)=c2a21-ca22
(7)
联合式(6)和式(7)得
(8)
a22=a11
(9)
则式(1)改写为
x′=a11(x-vt),
(10)
根据式(10)容易证明运动的相对性条件.由式(10)得逆变换关系为
x=a11′(x′+vt′),
(11)

下面求系数a11.某一参考系中,在同一地点先后发生的两事件的时间间隔称为固有时[6].而在其他任意参考系中观察到的这两事件的时间间隔称为普通时.根据式(10),有Δt′=a11Δt, (Δx=0)
(12)
其中,Δt为在S系中的固有时.另外,根据式(11)有
(13)

a11=γ
(14)
把式(14)代入式(10)得洛伦兹变换公式:
(15)
2 四维洛伦兹变换、间隔不变性与光速不变原理的等价性
下面研究4维时空的洛伦兹变换公式.令
x′=γ(x-vt),
y′=φ1y,
z′=φ2z,
(16)
设S′系中,在t′=0时刻坐标原点O′发出一束沿y′轴传播的光,在S系看来光路如图1所示.根据光速
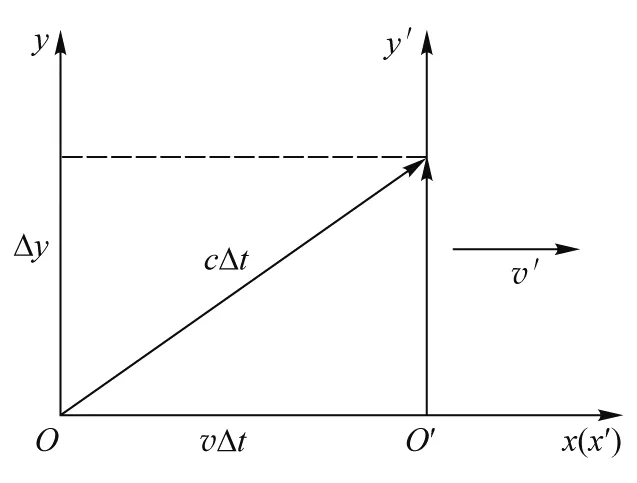
图1 光路图
不变原理有
c2Δt2=v2Δt2+Δy2,
cΔt′=Δy′
(17)
由于Δt′为固有时,有Δt=γΔt′,另外,根据式(16)有,Δy′=φ1Δy,分别代入式(17)可得:φ1=1.同理可得,φ2=1.于是有洛伦兹变换关系:
x′=γ(x-vt),y′=y,z′=z,
(18)
上述推导洛伦兹变换关系的过程只利用了相对性原理和光速不变原理,反过来从洛伦兹变换可以得到两惯性系间速度变换关系,从而也很容易证明光速不变原理[6],因此在相对性原理假设下,光速不变原理与洛伦兹变换关系是等价的.前面的推导表明光速不变原理保证了运动的相对性条件成立,因此根据文献[6]的推导,也就证明了光速不变性与间隔不变性是等价的.同时还可以证明洛伦兹关系与间隔不变性也是等价的[9].因此,光速不变原理、洛伦兹变换关系和间隔不变性三者在物理上是等价的.
3 总结
综上所述,通过相对性原理和光速不变原理不仅可以得到洛伦兹变换关系,从而保证运动的相对性条件的成立,同时证明了在相对性原理的条件下,光速不变原理、间隔不变性和洛伦兹变换关系三者等价.
