基于蒙特卡罗模拟的三维氢原子电子云可视化
2022-06-10曹宇晗吕恒鑫熊天宇卢紫萱鄂依婷
曹宇晗,吕恒鑫,熊天宇,卢紫萱,鄂依婷,徐 磊,舒 崧
(湖北大学 物理与电子科学学院,湖北 武汉 430062)
量子力学中微观粒子的空间存在状态是一个很难理解的物理图像,尤其是氢原子的电子云图像.一般量子力学教材中只会分别单独给出氢原子电子云的径向分布图像和角向分布图像,并不是完整直观的三维空间图像.本文希望从氢原子薛定谔方程的波函数解出发,采用蒙特卡罗模拟方法,结合Mathematica软件编程具体绘制出完整的氢原子电子云的三维空间可视化图像[1,2].这样可以更好地呈现微观粒子空间存在的量子性图像,并作为量子力学课程的重要教学资源.
蒙特卡罗方法是随机模拟方法和统计实验方法的别称,它是通过产生一系列随机数来模拟各种随机过程的数学方法.在按蒙特卡罗方法抽样时,可以具体采用反函数法,舍选法,Metropolis随机游走法等抽样方法.本文在模拟氢原子的电子云时采用的是舍选抽样法[3-5].
大学量子力学课程教学中通常存在课程内容抽象,物理图像不直观的问题.许多量子系统在求解出系统的波函数后,学生仍然很难对波函数所反映出的物理图像有直观的理解和把握.比如,传统的量子力学教材在讲解氢原子电子云的图像时一般会给出电子在径向和角向上的概率密度函数.但是,学生只能通过概率密度函数大概想象电子云的疏密程度,无法直观地了解电子云真实的三维形态.有的论文和书籍会给出电子云的二维图像,这样可以进一步加深学生的理解,但是仍无法做到让学生对电子云图像有一个清晰全面的认知.本文主要目的就是结合蒙特卡罗模拟方法提供一个简单易行的解决方案,具体针对三维空间电子云图像的可视化开发一套易于操作和实现的算法和程序,只要通过输入径向和角向的概率密度函数即可得到对应系统的三维电子云图像.通过本文给出的算法还可以实现氢原子任意量子态的三维电子云可视化,可以实现量子力学课程中比较常见的微扰系统的波函数的可视化,比如:弱电场中的氢原子系统,有自旋轨道耦合的氢原子系统等系统的三维电子云可视化,有着很强的实用性和可推广性,并且可以很方便的应用到相关课程资源的开发过程中.量子力学中各种系统的三维电子云图像可以加深学生对量子力学的理解,帮助学生对量子力学中微观粒子存在的物理图像有一个直观的认识.
1 氢原子中电子的波函数
为简化问题,我们研究的对象是处于定态的氢原子.对于氢原子,是单电子情形,其含时薛定谔方程为
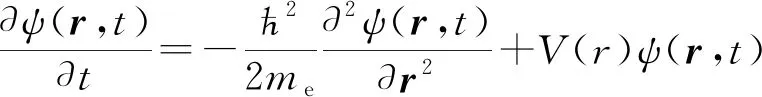
(1)
其中势能函数是
(2)
采用分离变量的方法
ψ(r,t)=ψ(r)T(t)
(3)
其中ψ(r)是波函数中的空间演化部分,T(t)是波函数中的时间演化部分.将分离变量后的波函数代入到含时薛定谔方程得到
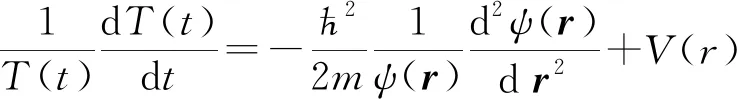
(4)
解得
(5)
其中E为定态能量,则波函数的定态解为
(6)
我们由波函数的概率诠释
P(r)=ψ*(r,t)ψ(r,t)=ψ*(r)ψ(r)
(7)
可知定态氢原子电子云的概率分布不含时,进一步我们可以得到定态薛定谔方程:
(8)
其中ψ(r)为氢原子中电子的空间波函数[6],考虑到系统的球对称,可按径向和角向进行分离变量:
ψ=ψnlm(r,θ,φ)=Rnl(r)Ylm(θ,φ),
(n=1,2,3,…;l=0,1,…,n-1;m=±1,±2,…,±l)
(9)
其中Rnl(r)为径向波函数,Ylm(θ,φ)为球谐函数,n、l、m分别为主量子数、角量子数和磁量子数.径向波函数Rnl(r)为
(10)
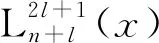
WR(r)=|Rnl(r)|2r2
(11)
角向波函数为球谐函数,对球谐函数Ylm(θ,φ)再次分离变量,有
Ylm(θ,φ)=Θ(θ)Φ(φ)
(12)
其中方位角波函数Φ(φ)为
(13)
由波函数的概率诠释可知,方位角函数的模方|Φ(φ)|2表征的是定态氢原子电子云在方位角上出现的概率,其值为常数1/(2π),这表明电子云的分布具有绕z轴的旋转对称性.而仰角波函数Θ(θ)为
(14)
其中Mlm是归一化系数,Plm(x)是缔合勒让德函数,由波函数的概率诠释可知,定态氢原子电子云在仰角方向上的概率密度函数为WΘ(θ),即
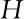
(15)
我们通过文献调研发现,现有对氢原子电子云分布的可视化研究大多数将氢原子波函数拆分为径向分布函数和角向分布函数,利用径向波函数绘出定态氢原子电子云二维径向概率分布图,以及利用球谐函数作出三维角向概率分布图来体现出其在z轴方向上的旋转对称性,或者是作出氢原子电子云空间分布的某一角度剖面图,并未有真正意义上的三维氢原子电子云空间分布呈现.本文直接对氢原子薛定谔方程的波函数解在完整的三维空间使用蒙特卡罗模拟方法进行抽样,通过Mathematica软件编程实现氢原子电子云任意量子态的三维可视化,让氢原子电子云图像的呈现更加直观,能够作为重要的教学资源让学生更加简单地理解复杂抽象的物理图像.
2 电子云的蒙特卡罗模拟
电子云存在于三维空间中,为了画出三维氢原子的电子云,首先需要按照电子的波函数抽取一系列电子的空间坐标,本文接下来利用蒙特卡罗方法中的第一类舍选法进行抽样.由于电子的波函数是可分离变量的,所以我们可以将波函数按坐标变量r、θ、φ分为3个部分,然后按对应的概率密度分别对3个坐标进行抽样,最终得到电子随机出现位置的空间坐标[7].
首先,由于第一类舍选法只能抽取有限区间内的随机数,但是r的取值范围是[0,∞],为了满足第一类舍选法的条件,我们要对r的取值范围进行截断.为了确保径向方向上大部分的点可以被取到,并且使得图形中呈现完整美观的电子云图像.通过调整不同的截断范围进行比对,最终决定保留r方向上80%的电子可以被取到所对应的区间,确定r的取值范围为r∈[0,rM].
然后,我们对r进行抽样时, 在r的取值范围[0,rM]中计算出电子的概率密度函数WR(r)及其最大值M,然后我们在[0,rM]内产生一均匀分布的随机数ri,并且在区间[0,1]产生一均匀分布的随机数ai.比较随机数ai与WR(ri)/M的大小,如果
ai≤WR(ri)/M
成立,则将ri保留为一个抽样值,如果不成立,则舍去ri.重复上述过程,直到得到一系列数目足够的抽样值{ri}.
抽样的结果如图1所示.图中实线对应径向概率密度分布函数曲线,直方图表示的是所抽取的径向的随机点样本的频率分布,横轴为径向距离,单位长度a0为一个玻尔半径.
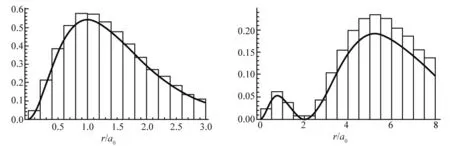
n=1, l=0 的径向概率密度函数 n=2, l=0 的径向概率密度函数
接下来我们对θ进行抽样,首先,根据球坐标中θ的定义可以确定θ的取值范围为θ∈[0,π].然后在θ的取值范围[0,π]内计算出电子的概率密度函数WΘ(θ)及其最大值M2,然后我们在[0,π]内产生一均匀分布的随机数θi,并且在区间[0,1]产生一均匀分布的随机数bi.比较随机数bi与WΘ(θi)/M2大小,如果
bi≤WΘ(θi)/M2
成立,则将θi保留为一个抽样值,如果不成立,则舍去θi.重复上述“产生两组随机数然后进行判别”的过程,直到得到一系列数目足够的抽样值{θi}.
抽样的结果如图2所示.图中实线对应仰角概率密度分布函数曲线,直方图表示的是所抽取的仰角的随机点样本的频率分布,横轴为仰角大小.

l=1, m=0的仰角概率密度函数 l=2, m=0的仰角概率密度函数
最后抽取φ的随机数,φ在取值范围[0,2π]内均匀分布,所以我们可以直接对φ用均匀分布抽样,得到一组抽样值{φi}.
这样,我们就得到了3组抽样值{ri}、{θi}、{φi},将三组抽样值构造成随机点的球坐标(ri,θi,φi),然后在Mathematica中再将这些点的球坐标转化为直角坐标,这样就得到了一系列电子的空间坐标点(xi,yi,zi).
3 电子云的三维图像可视化
得到一系列空间坐标后,我们可以借助计算机程序设计语言和编程软件实现氢原子电子云的图像模拟,我们在这里使用Mathematica为平台运行程序.根据以上结果编写与运行程序,通过改变不同量子数可得到对应的三维电子云图像[8].
在电子云的图像中,每一个点代表电子可能出现的空间位置,点的密集程度代表了电子在此处出现的几率的大小[9].某处的点越密集,说明电子在此处出现的概率越大.我们可以借助概率密度函数图像来说明电子云分布图像.注意到量子数为n=1,l=0和n=2,l=0的径向概率密度函数如图1所示,量子数为l=1,m=0和l=2,m=0的仰角概率密度函数如图2所示.
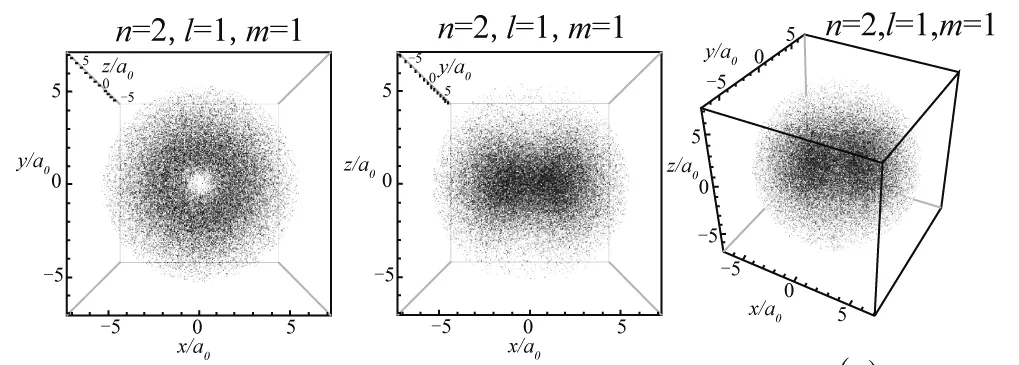
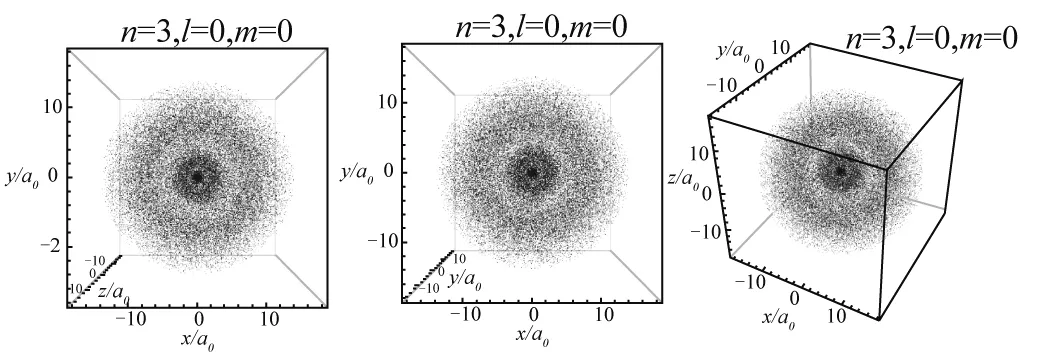
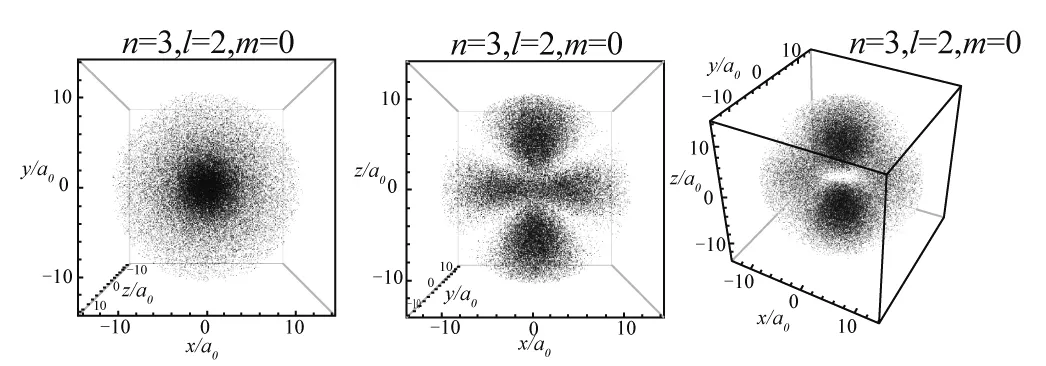
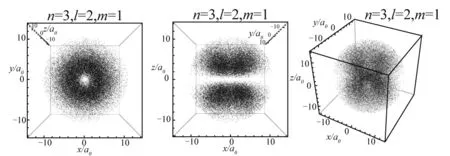
图3—10展示8组典型量子数的氢原子电子云顶视图、正视图和缺省视图.
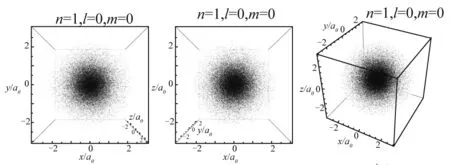
顶视图 正视图 缺省图
当l=0时,电子云图在空间中呈现各向同性,无角向变化,等概率密度面均为球面,径向概率密度函数的峰值体现在电子云在对应半径的球面附近分布相对集中.如图1所示,在n=1时径向概率密度函数有一个峰值,n=2时径向概率密度函数有两个峰值,反映在图3和图4中,n=1时电子云呈现球状分布结构,在一个玻尔半径处分布最密集,体现出氢原子核外电子在绕核一个玻尔半径的球面附近出现的概率极大;而当n=2时呈现出电子云有一大一小两个球壳面出现密集分布,以同一球心套在一起,与图1的峰值出现情况相符.同理,n=3时氢原子电子云分布呈现3个不同半径的同心球壳上出现概率极大的状态.
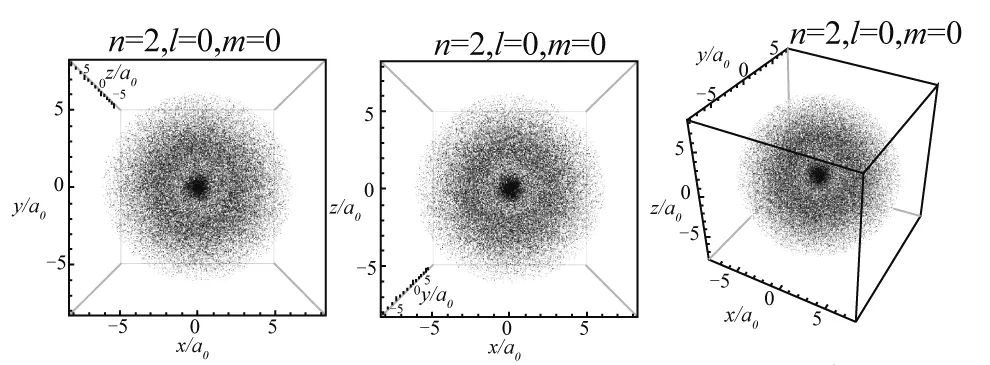
顶视图 正视图 缺省图
当l=1时,由图2(a)可以看出仰角概率密度函数有两个峰值,反映在图5上为m=0时的电子云的三维分布为上下两个部分的哑铃型,当l=2时,图2(b)上反映出仰角概率密度函数有3个峰值,我们可以看到图8中电子云分布在空间不同仰角上呈现出3个相对集中的区域.当m=1和m=2时,由于磁量子数的影响,电子云呈现不同方向的分布.更一般地,仰角概率密度函数的极大值点个数为S=l-|m|+1.电子云图可以很直观的同时体现出氢原子核外电子在空间中不同径向距离和不同方向上出现的概率分布.
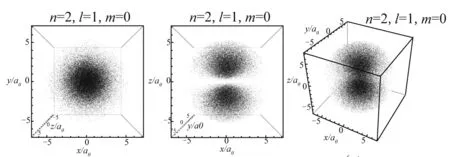
顶视图 正视图 缺省图
顶视图 正视图 缺省图
顶视图 正视图 缺省图
顶视图 正视图 缺省图
顶视图 正视图 缺省图
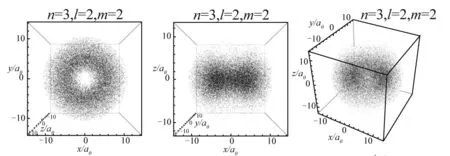
顶视图 正视图 缺省图
4 总结
本文通过求解氢原子薛定谔方程的波函数解,使用蒙特卡罗模拟的方法,在Mathematica软件编程环境下,绘制出了氢原子电子云各能级的三维空间可视化图像.实现了完整的三维氢原子电子云空间呈现,可以让氢原子核外电子的行为变得直观,用在课堂教学中,能够作为重要的教学资源给学生以清晰的了解和学习.同时,可以让学生对基础物理有更加深刻的理解,产生更加浓厚的兴趣.我们还会继续研究,开发各种受微扰的原子系统的电子云的三维空间可视化模拟,并希望未来可以脱离Mathematica软件,开发出独立的、可交互的原子三维空间电子云模拟平台软件并作为量子力学课程的可视化教育资源.
