基于局部敏感和分组稀疏的鲁棒人脸识别

孙 茜

(安徽邮电职业技术学院 计算机系，安徽 合肥 230031)

人脸识别是模式识别和计算机视觉领域内一项最具有挑战性的研究课题。它除了具有科学意义外，还在商业、执法等其他领域中有许多应用，如监督、安全、通信和人机交互等。经过30多年的研究，研究者提出了许多人脸识别方法，但由于表情、发型、光照和不同人群之间的面部器官分布的相似性致使鲁棒的人脸识别仍然是一个开放研究的问题。

在过去的几年中，由于压缩感知的兴起，特别是作为其核心技术的稀疏表示，不仅可以降低数据分析和处理的成本，而且提高了数据压缩的效率。基本稀疏表示的方法由于其优良的性能以及对噪声和遮挡的鲁棒性，受到了广泛的关注。在2009年，J.Wright等人提出稀疏表示方法SRC[1]，用以解决人脸识别问题。稀疏表示主要是在训练数据字典中寻找测试样本最稀疏的表示方法，在分类中是有效且鲁棒的，但没有考虑训练数据字典的内部结构信息。M.Yang等人在2010年提出基于Gabor特征的稀疏表示方法GSRC[2]，使用图像的局部Gabor特征用于稀疏表示之中。GSRC的显著优势在于它使用了紧凑的遮挡字典，大大降低了稀疏编码的计算代价，但仍没有考虑到字典的内部结构信息。同时，J.Simon等人关注到字典内部组别问题[3]，2011年E.Elhamifar等人提出了一种更鲁棒的分类方法，即分组稀疏表示方法[4]，这种方法主要是寻找测试样本的最小块数表示，克服了SRC的缺点，但丢失了数据的局部性结构。近几年，稀疏表示方法有了越来越多的研究与发展，例如2013年提出的基于核函数的稀疏表示方法KSRC[5-11]，2014年提出的判别组稀疏字典学习算法DGSDL[12]。之后，基于核函数稀疏学习的方法也得以精进[13]，R.Abiantun等人关注到姿势变化对于稀疏学习的影响[14]，2015年由X.Jiang等人提出用于处理人脸识别任务的通过字典分解的稀疏与稠密相混合的表示方法SDR[15]，2016年N.Zhang等的基于极限学习机的稀疏表示人脸识别方法[16]。2017年张涛、吴键提出基于PCA和SRC的人脸识别算法[17]，2018年木立生、吕迎春提出基于稀疏表示与特征融合的人脸识别方法[18]，2019年王国权、巩燕提出小波分析和稀疏表示的人脸图像识别方法[19]，2020年吴庆洪、高晓东提出稀疏表示和支持向量机相融合的非理想环境人脸识别算法[20]。

本文提出了一种将局部敏感稀疏性与分组稀疏相结合的新方法，它不仅考虑了训练数据字典的分组结构信息，而且集中了数据的局部性，该方法旨在学习分组稀疏和数据局部性的同时，实现分类性能的提高。

1 稀疏表示

1.1 稀疏表示分类

SRC算法可以被视为一个将输入图像转化为具有光照、表情等训练图像的线性组合的过程。假设有n组，第i类有ni个训练样本，ai,j∈RD×1表示第i类中的第j个人脸样本图像，所构成的D表示图像特征向量的维数，Ai=[ai,1,ai,2,…,ai,ni]∈RD×ni包含第i类的训练图像。A=[A1,A2,…,An]表示全部的训练集，y代表一个输入测试图像。为避免l0模引起的NP-hard问题，SRC通常使用l1模最小化约束进行分类：

(1)

其中，x是稀疏系数特征，ε是与有界能量的噪声项相关的参数。x*T=[x1*T,x2*T,…,xn*T]表示最优解，xi包含着第i类的相关系数。

1.2 分组稀疏分类

SRC算法虽然已获得很好的识别性能，但一个潜在的问题在于SRC算法中测试图像可能是被不同对象的训练样本所表示出来。在人脸识别过程中，这个问题容易造成错误的识别。理论上，测试图像应该只被其对应对象的训练图像所表示。基于这个思想，Elhamifar等人提出一种更为鲁棒的分组稀疏表示分类方法，该方法主要是用尽可能少的对象的训练图像表示出测试样本，首先将训练数据字典划分为不同组，每一组由来自同一个对象的训练图像组成，然后搜索出一种在进行识别时使用最少分组数目的表示方法。这等价于将分类问题转化为结构稀疏恢复问题。

给定一个测试图像y,通过以下的凸问题得到稀疏系数x，从而最大限度地减少字典中的非零组数目。

(2)

其中，xi表示第i类相关的系数，ε是相关噪声参数，A=[A1,A2,…,An]表示一个完整的训练集。

除了最小化非零组数目，另一种优化方法是最小化非零重构向量Aixi。

(3)

其中，Ai=[ai,1,ai,2,…,ai,ni]∈RD×ni表示第i类训练样本。

从式(2)和式(3)中可以看出，只有当这些分组由线性无关数据组成时，它们才是等价的。由于人脸之间器官分布的相似性，在人脸识别应用中很容易出现线性相关的数据。

2 局部敏感性稀疏和分组稀疏的人脸识别

目前在许多模式识别问题中，数据局部性得到了广泛的应用，如K近邻分类器、数据聚类和图像分类等。有研究指出，数据的局部性比稀疏编码的稀疏性更为适用于分类识别。因此，我们提出了一种改进方法，将局部敏感的稀疏性和分组稀疏相结合。

首先，本文算法考虑分组稀疏表示中的一种形式，即字典中的最小化非零组数目，通过将l1模最小化问题置于特征空间中考虑数据的局部性。本文算法中l1模最小化问题可以写成如下形式：

(4)

其中λ是一个正则化参数，符号·代表点乘计算，x表示稀疏系数向量，β用于对分组稀疏进行加权，A=[A1,A2,…,An]是所有类的训练样本，y表示一个测试样本，ε是相关的噪声参数，xi是与第i类训练样本相关的表示系数，p是局部适配器，本文所提算法使用类似于LS-KSRC算法中的指数局部适配器：

(5)

其中，η是一个正值参数，yi表示一个测试样本，yj表示一个邻近yi的训练样本，d(yi,yj)由l2模计算如下

d(yi,yj)=‖yi-yj‖2

(6)

其中，d(yi,yj)表示欧氏距离。

在式(4)中，向量p被用于度量测试样本与每一列训练样本之间的距离，换言之，向量p可以被视为一个差异向量，主要用于约束对应的稀疏系数。由于大部分系数均为0，只有少量的有效系数值，因而式(4)可以被视为l1模下的稀疏表示，而非l2模。则式(4)的最小化问题可以理解为用邻近的训练样本去编码表示出测试样本，使所获得的最优稀疏系数既有分组稀疏性，也包含数据的局部结构。这保证了本文所提算法可以较好地学习到用以分类的判别稀疏表示系数。

同理，本文考虑了另一种分组稀疏表示的优化形式，即考虑最小数目的非零重构向量，则本文所提算法的l1模的最小化问题可表示如下：

(7)

其中，Ai∈RD×ni是训练样本中i类的子集。

需要指出的是在式(4)和式(7)中，第一项约束了数据的局部性，可以保留测试样本与其邻近的训练样本之间的相似性，并给出具有判别性信息的稀疏表示系数。第二项约束了分组稀疏性，将训练数据内部的分组结构信息加以利用。因而，本文所提算法在使用了分组稀疏约束的同时，也考虑了数据的局部结构。该算法的流程总结如下。

1)输入：训练样本矩阵A,一个测试样本y

2)通过局部适配器p计算测试样本与每一个训练样本之间的差异向量

3)解决l1模最小化问题

5)输出：给出测试样本的类标签class(y)=argmini=1,2,…,nri(y)

3 实 验

本文在ORL、AR和Extended Yale B数据库上对所提出算法进行了识别性能测试。图1展示了来自这3个数据库中的几个样本图像，它们往往有不同的姿态、表情和光照。为了验证本文算法的优越性，本文将提出的算法与几个相关的稀疏表示人脸识别算法的识别率进行比较。

在实验过程中，使用PCA方法[26]对分类前的特征进行降维，使用CVX工具箱解决l1模最小化问题。本文设置实验参数ε=0.05，η=0.5，由于算法和数据库不同，需要通过设置不同的λ和β以实现最优的性能。为了公正的比较，实验中测试了多种参数值设置，并记录下它们的最优性能。

图1 3个人脸数据库的样本图像

3.1 ORL数据库实验

在本实验中，在ORL数据库上测试了在不同训练与测试百分比下不同算法的识别性能。ORL数据库包括40个对象的400张不同姿态、光照和面部表情下的人脸图像。每次测试时，随机选择每个对象的L张图像作为训练集，其余图像作为测试集。识别率取30次随机测试结果的平均值。表1是不同算法的识别率结果。

表1 ORL数据库上的识别性能对比 单位：%

表1所示，在不同训练/测试比例设置下，本文所提出的P3和P4算法明显优于其他算法，包括SRC，LS-KSRC以及两种形式的分组稀疏算法。P3算法在30%训练百分比设置下实现了90.357%的识别性能，在训练比为40%实现了94.167%的识别率，50%时为97.000%。P4算法在30%训练比下实现了94.286%的识别率，40%时为95.417%，50%时为98.000%。由表1还可以看出，P4算法一般可以实现最优的识别性能。例如在L=3时，P4算法的识别率高于SRC算法8%左右，高于LS-KSRC算法4.643%，比P1算法优6.429%,比P2算法优5%，甚至比P3算法优出3.929%的识别率。这些都表明本文提出算法是一种相较于其他已知的几种算法更有效的人脸识别分类方法。

3.2 AR数据库实验

本实验中，不同算法将在AR数据库上进行不同PCA降维设置下的性能对比，AR数据库包含126个对象的3 276张不同姿态、表情和光照的人脸图像。原始的图像大小是165*120，实验时选择100个对象的1 400张图像作为一个实验子集，保证对于每一个对象有14张正面人脸图像。每次测试时，随机选取每个对象7张图像作为训练数据集，其余的图像作为测试训练集。与ORL数据库上进行的实验一样，统计30次的随机测试结果的平均值作为识别率记录下来。表2给出了不同算法在不同PCA特征降维设置下的最优识别率。

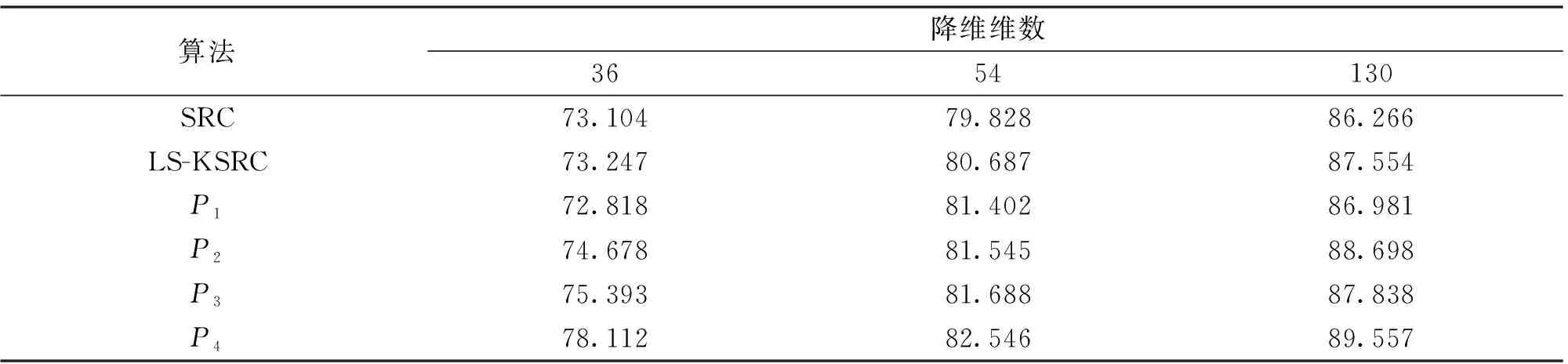
表2 AR数据库的识别性能对比 单位：%

正如表2所示，本文提出的P3和P4算法显示了它们相较于其他算法在不同PCA降维设置下的优越性。在36维时P3算法最高的识别率为75.393%，在54维时为81.688%，130维时为87.838%。P4算法显示出了比P3算法更好的识别性能，在36维时达到78.112%，在54维时达到82.546%，130维时为89.557%的识别率。这些识别率都再次证明本文所提算法的优越性，尤其是在低维情况下。当降维数为36时，P3算法可以实现高于SRC算法2.289%的识别性能，高于LS-KSRC算法2.146%,高于P1算法2.575%；而P4算法可以实现优于SRC算法5.008%的识别性能，分别优于LS-KSRC和P2算法4.865%、3.434%。

3.3 Extended Yale B数据库实验

Extended Yale B数据库是由38个对象的2 414张正面脸部图像组成，每一个对象均有64张大小为192*168的不同光照下人脸图像。实验时选择每个对象的32张图像作为训练图像，剩下的作为测试图像。表3是不同算法在不同PCA降维设置下的最优识别率。

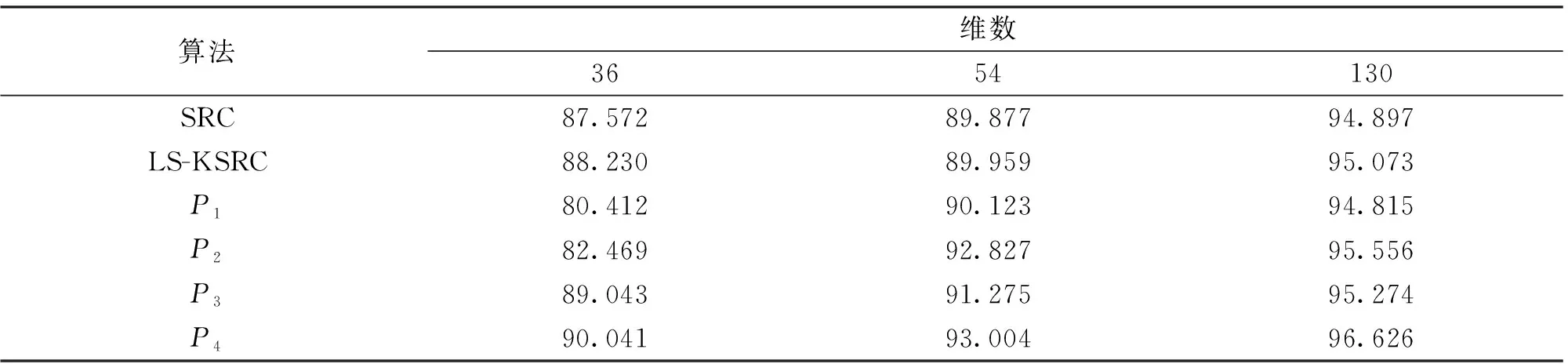
表3 Extended Yale B数据库上的性能对比 单位：%

从表3可以看出，本文所提出的算法仍然比其他方法的性能要优异。P3算法在特征维数为36时获得最优识别率89.043%，54维时最优为91.275%，130维时最优为95.274%。在低维情况下，本文算法展现出了明显优于其他算法的分类识别性能，这与AR数据库上进行的实验测试结果一致。例如，当特征维数降为36时，P4算法获得的最优识别率为90.041%，相较于SRC的识别性能高出2.469%，优于LS-KSRC的识别性能1.811%，比P1算法高出9.629%，比P2算法高出7.572%。P4算法在特征维数为130时可以实现最高的识别性能，达到96.626%的识别率。

4 结 论

本文提出了一种新的分类方法，即使用局部敏感稀疏和分组稀疏来进行鲁棒的人脸识别。这种方法同时学习了分组稀疏性和数据局部性，不仅考虑了训练数据字典的分组结构信息，也整合了数据的局部性，这样可以学习更多的可判别稀疏表示系数用以人脸识别。为了测试本文所提方法的有效性，在ORL、AR和Extended Yale B数据库上展开了人脸识别的实验，并与其他分类识别算法进行对比验证了本文算法的优越性能。