强非局域介质中复宗量厄米-高斯型空间光孤子

王形华,陈荣泉,王 清

(1赣南师范大学物理与电子信息学院,江西 赣州 341000;2闽南理工学院土木工程学院,福建 泉州 362799;3九江学院理学院,江西 九江 332005)

0 引言

涡旋光束是一种携带轨道角动量的新型光束,在光通信中有独特的应用价值。2007年,Dai等[1]用分离变量法研究了涡旋光束在强非局域非线性介质中传输的规律,光束会绕传输方向旋转,光强在径向的分布呈现单环或多环结构。Chen[2]研究了复宗量拉盖尔-高斯光束在强非局域非线性介质中的传输。Zhang等[3]用解析法分析得到,在一定条件下共线传输的复宗量厄米-高斯型光束演化为涡旋光束,束宽呈现周期性变化。2013年,Martinez-Castellanos对复宗量涡旋光束的研究中,得到了复宗量分数阶拉盖尔-高斯光束,会出现涡旋的产生、湮灭和横切面上运动的现象[4]。2016年,Zhu[5]研究了复宗量涡旋厄米-高斯光束在大气湍流中的传播,可以通过减小波长和拓扑电荷或者增大高斯束腰,有效地控制光束的扩散。

复宗量厄米-高斯光束是波动方程在旁轴近似下的近似解析解,是一种参量满足复数函数的光束,相比厄米-高斯光束具有更复杂的光强和相位结构。本文研究(1+2)维复宗量厄米-高斯光束在强非局域过程中的传输特性,分析在不同阶数情况下光强、束宽和角动量的变化规律;并在此基础上探讨涡旋呼吸子在不同传输距离上的截面光强和相位图,研究不同阶数以及传播距离对该涡旋光束扩展的影响。

1 理论模型

在非局域非线性介质中,光束的演化规律可以由归一化的非局域非线性薛定谔方程(NNLSE)来描述[6-10],即

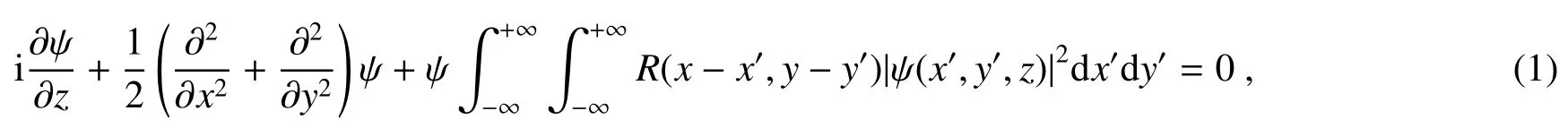
式中:ψ 是输入光束波函数;z是纵向坐标;x和y代表横向坐标;是诱导的非线性折射率,其中R代表响应函数,这里采用高斯型响应函数,因为它可以比较容易地得到孤子在非局域介质中的传输规律

式中σ为特征宽度。复宗量厄米-高斯涡旋光束可以表示为

式中:A是振幅,a是光束宽度,m是阶数。为厄米多项式,且 ξ=x+iy。对于高阶孤子,在x和y方向上的光束统计宽度可以定义为

光束椭圆率可以定义为

孤子的功率和轨道角动量OAM[11,12]可以分别表示为

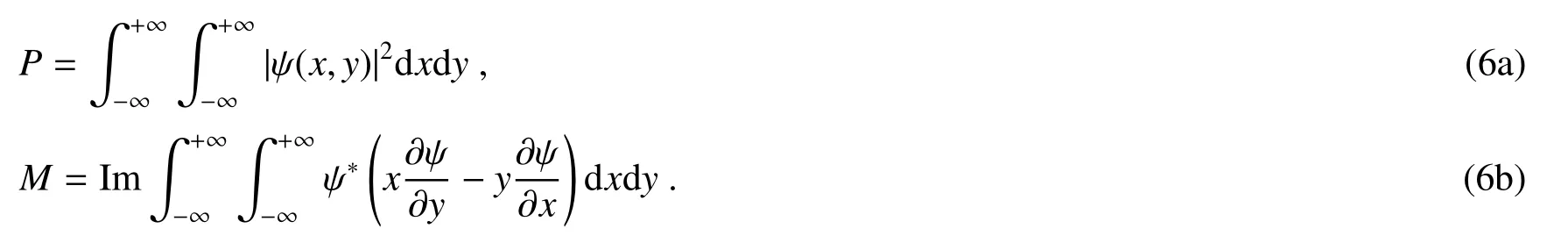
2 数值模拟结果与分析

为了方便讨论,响应函数特征长度和束宽分别取为σ=20和a=1。采用成熟的分步傅里叶法数值模拟复宗量厄米-高斯涡旋光束在此强非局域介质中的传播。一般来说,非线性和衍射效应是同时起作用的。如果传输步长取得足够短,则每一步传输时可以近似地处理为衍射和非线性分别单独作用[13],这就是分步傅里叶法。

2.1 复宗量厄米-高斯光束的强度分布与相结构图

不同阶数情况下,复宗量厄米-高斯光束的强度分布和x、y方向上相应相位结构分别如图1、2所示。图1表明,复宗量厄米-高斯光束的强度和相位分布非常复杂,并且随着阶数而变化产生了一些新颖的传播特性。光束强度变化如图1中(a1)、(b1)、(c1)、(d1)所示,其表明当阶数m增大时,光束束宽也相应增大,但是涡旋奇点的个数与阶数相等;相位结构变化如图1中(a2)、(b2)、(c2)、(d2)所示。光束传输过程中光斑将发生旋转,旋转方向取决于表达式ξ=x+iy中虚部前的符号,虚部前的符号取正时,光斑沿着逆时针方向旋转;虚部前的符号取负时,光斑沿着顺时针方向旋转。复宗量光束旋转的物理本质在于其光束横向能流分布不均匀[14]。而常规厄米-高斯光束没有涡旋相位,并且在传输过程中不会旋转。

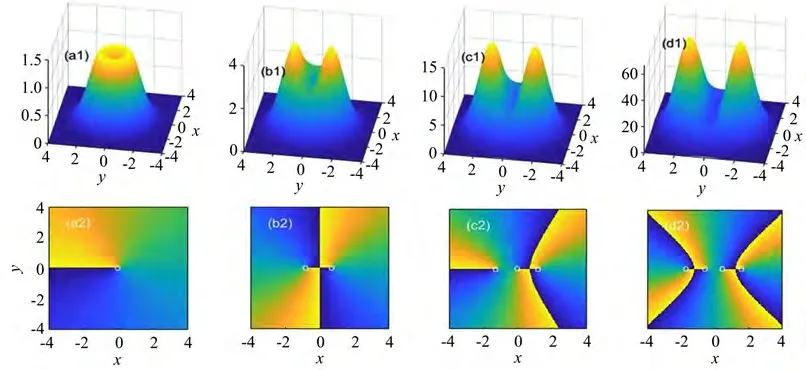
图1 复宗量厄米-高斯光束的强度分布[(a1)～(d1)]和相应的相结构[(a2)～(d2)]。选择参数为A=1;(a1),(a2)m=1;(b1),(b2)m=2;(c1),(c2)m=3;(d1),(d2)m=4Fig.1 Intensity distributions[(a1)～(d1)]and the corresponding phase structures[(a2)～(d2)]of the complex variable Hermite-Gaussian beams with A=1;(a1),(a2)m=1;(b1),(b2)m=2;(c1),(c2)m=3;(d1),(d2)m=4

由图2可知,光强分布在x和y轴方向的分布是不一样的,x轴方向的光强奇异点(光强为0)与阶数m相等,但是y轴方向的光强奇异点与阶数m无关。

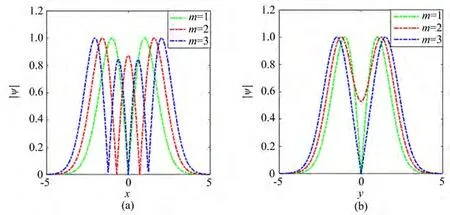
图2 不同阶数的复宗量厄米-高斯光束在x和y方向的归一化光强分布Fig.2 The normalized intensity distribution for different orders of complex variable Hermite-Gaussian beams in x and y directions

2.2 复宗量厄米-高斯呼吸子

复宗量光束表达式中参数ξ=x+iy是复数,一般具有涡旋光的性质。图3为二阶(m=2)复宗量厄米-高斯光束在非局域介质中传播时光斑结构随传播距离的变化。由图3(a)可知,当光束的输入功率小于临界功率(光束束宽不变形成孤子时所对应的功率)时,光束束宽周期性地先扩展后压缩,传输中光束束宽总体大于临界束宽(孤子的束宽),周期比图3(b)的大;由图3(b)可知,当光束的输入功率等于临界功率时,光束束宽保持不变,保持稳定传输;由图3(c)可知,当光束的输入功率大于临界功率时,光束束宽周期性地先压缩后扩展,传输中光束束宽总体小于临界束宽,周期比图3(b)的小。图3(a)、(c)即为复宗量厄米-高斯呼吸子。

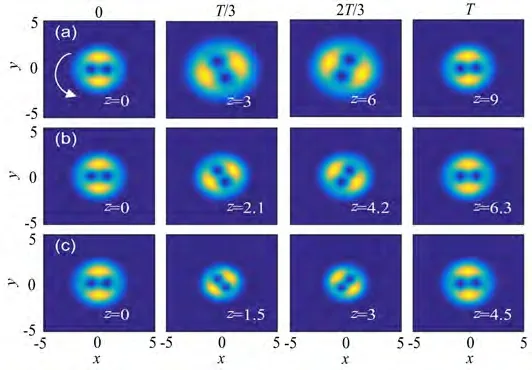
图3 复宗量厄米-高斯光束在非局域介质中传播,选择参数为m=2,(a)P0=129000,(b)P0=258000,(c)P0=515000Fig.3 Propagation of the complex variable Hermite-Gaussian breathers in the nonlocal media.Parameters are chosen as m=2,(a)P0=129000,(b)P0=258000,(c)P0=515000

2.3 复宗量厄米-高斯孤子

图4为不同阶数情况下复宗量厄米-高斯孤子在传播过程中的光斑结构变化。由图4可知,随着阶数m增加,涡旋奇点个数增多,光束束宽和椭圆率增大,但是临界功率和旋转周期不变。图5为一个周期内复宗量厄米-高斯孤子的波形轮廓图。由图5可知,不同阶数m情况下,光束在传输一个周期后的波形与初始波形基本重合,说明光束在传输过程中波形可以基本保持不变;当m增大时,光斑中间区域光强为0的点增多,光强在x轴方向的分布更加复杂。

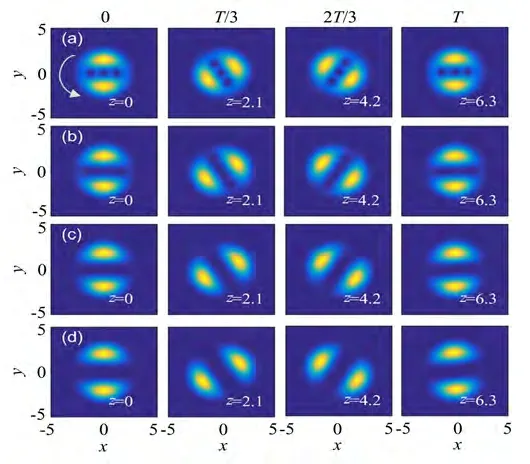
图4 非局域介质中的复宗量厄米-高斯孤子的传播,选择参数为P0=258000,(a)m=3,(b)m=4,(c)m=5,(d)m=6Fig.4 Propagation of the complex variable Hermite-Gaussian solitons in the nonlocal media.Parameters are chosen as P0=258000,(a)m=3,(b)m=4,(c)m=5,(d)m=6

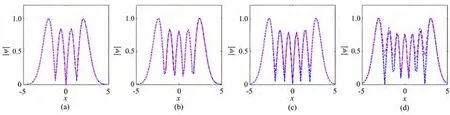
图5 入射(z=0,蓝线)和传输一个周期(z=6.3,粉红线)处光束波形对比,各参量取值与图4相同Fig.5 Comparison of beam waveforms at incident(z=0,blue line)and one transmission period(z=6.3,pink line).Values of each parameter are the same as those in Fig.4

图6为不同阶数情况下复宗量厄米-高斯孤子的相位变化情况。由图6可知,光束在横向截面上对应的相位结构类似“花瓣”结构,光束对应的阶数m越多,花瓣越复杂,且花瓣个数与m相等。在光束传输过程中,光束的相位结构稳定。

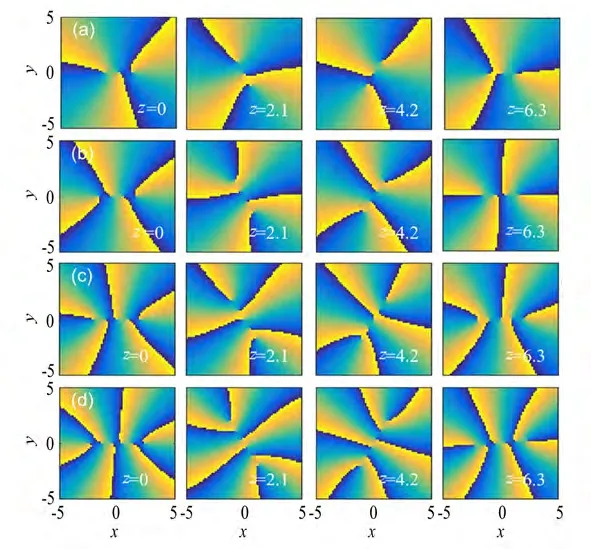
图6 复宗量厄米-高斯型孤子传输一个周期相位变化图,各参量取值与图4相同Fig.6 Phase variation diagram of a periodic transmission for complex variable Hermite-Gaussian soliton.Values of each parameter are the same as those in Fig.4

图7为临界功率和轨道角动量(OAM)与阶数m变化之间的关系。由图7可知,在不同阶数m情况下,形成稳定的光束涡旋孤子所需要的临界功率保持不变,而光束的轨道角动量会随阶数m的增大而增大。光束的轨道角动量也是分析光束信息的一个重要参量,理论上轨道角动量越大也可以使得光束进行更多的信息编码。当m=0时,复宗量厄米-高斯光束的轨道角动量为0,光束会退化为一般的高斯光束。Li[15]通过增大螺旋相位板的阶数得到近轴涡旋光轨道角动量增大的结果,在这里出现相似的现象。

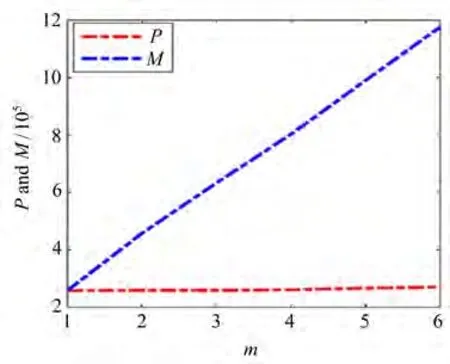
图7 复宗量厄米-高斯型孤子的功率和轨道角动量与m的关系Fig.7 The power and OAMs of complex variable Hermite-Gaussian soliton versus m

图8为x、y方向上的束宽在不同阶数m下的变化情况。由图8(a)可知,随着阶数m的增大,y方向的束宽变化明显大于x方向的束宽;由图8(b)可知,椭圆率η随着阶数m的增大而增大。光束在传输过程中,椭圆率η增大,两光斑分得越开,光斑变得更加扁长,显出更新颖的形状。

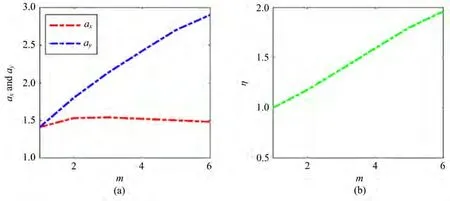
图8 (a)光束束宽与拓扑荷m的关系;(b)椭圆率η与拓扑荷m的关系Fig.8 (a)Beam width versus m;(b)Ellipticity versus m

2.4 稳定性分析

为了更严格地验证孤子的稳定性,需要考虑随机扰动的影响。简易做法为:给图4中的孤子在入射时添加一个随机扰动[16],可表示为A0[T(x,y)+βB(x,y)],A0代表孤子振幅,T(x,y)代表无微扰时的孤子解,B(x,y)是微扰项,β是微扰系数。一般来说,随机微扰都较小,因此取β=0.02来进行数值验证。图9为添加噪声后复宗量厄米-高斯孤子的传输变化情况,由图可见复宗量厄米-高斯型孤子可以在随机扰动下稳定地传播。

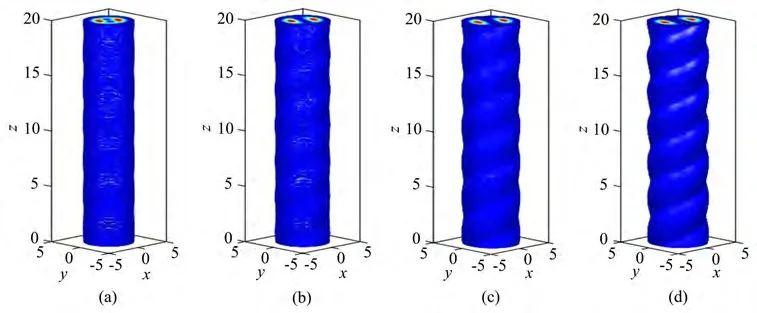
图9 非局域介质中加噪的复宗量厄米-高斯孤立子的演化,各参量取值与图4相同Fig.9 Evolution of the noise-added complex variable Hermite-Gaussian solitons in nonlocal media.The parameters are chosen as those in Fig.4

3 结论

运用分步傅里叶法模拟了复宗量厄米-高斯光束的传输,得到了一系列演化特性图,由图可见复宗量厄米-高斯光束具有轨道角动量和独特的光学涡旋结构。当复宗量厄米-高斯光束阶数m增大时,其椭圆率增大,即y轴方向的展宽大于x轴方向的展宽,使得光斑呈现y轴方向的拉伸;轨道角动量将增大,光学涡旋个数与阶数相等。光斑在x-y平面作逆时针方向的旋转。这些结果表明阶数越高的复宗量厄米-高斯光束在高斯型强非局域非线性介质中传输具有越多新颖的特性,可以在传输中携带更多信息,因此在信号传输方面具有潜在应用价值。独特的涡旋结构则可以应用在光镊、光学操控等方面。