量子行走中硬币与行走者纠缠关联的研究
2022-06-10张融,凌凯
张 融,凌 凯
(南京邮电大学光电工程学院,江苏 南京 210000)
0 引言
纠缠态广泛应用于量子隐形传态、量子密钥分发等,是量子信息处理过程中的重要资源[1-4],其中最大纠缠态与部分纠缠态相比,在完成部分具体信息处理任务时具有更高的效率和更好的性能。因此,制备和精确调控纠缠态以及最大纠缠态在量子技术应用中具有重大意义。纠缠通常是描述两个及多个粒子之间的量子关联,其定义还可以推广为单粒子不同自由度之间的量子关联,称之为组合纠缠(Hybrid entanglement)[5]。比如,单光子偏振与空间模式之间的纠缠关联。相比较两粒子之间的纠缠态,基于单粒子的组合纠缠有助于实现容错量子计算、探讨量子力学基本原理,其装置具有更加简单的结构和更低的损耗,从而易于实验实现[6-9]。
量子行走是经典随机行走在量子世界的对应模型[10],为实现量子计算、量子模拟等提供了很好的平台[11,12]。量子行走包括硬币和行走者两个子系统,硬币是二维的量子系统,而处于多个空间格点的行走者是高维系统。每一步演化包含两个操作,首先进行抛掷硬币操作,然后进行条件行走操作,即:行走者根据硬币状态在一维分立空间格点上向不同方向行走。量子行走中的条件行走操作是非局域操作,导致硬币和行走者之间产生纠缠关联,行走者可以处于多个不同的位置态,所以硬币和行走者之间的纠缠态是高维量子纠缠态。与传统的二维纠缠态相比,高维纠缠态能够存储更多的信息[13-15]。进一步研究发现,硬币和行走者整个系统的量子态可以通过硬币操作精确调控[16],从而实现最大纠缠态的调控。
本文探讨了基于量子行走实现硬币和行走者之间的纠缠关联。在具体物理实验中,通常用一个粒子的两个自由度分别表示硬币和行走者,比如,用光子的水平和竖直偏振表示两个不同的硬币态,用光子的位置状态表示行走者,因此这种情况下硬币和行走者之间的纠缠是组合纠缠。在之前的理论和实验工作中,通过在量子行走中添加随演化时间完全随机改变的位相无序,可以得到最大纠缠态,但是所需要的演化步数高达100步以上才能得到接近最大纠缠的量子态[17,18]。已有的研究成果表明,量子行走已在多个物理系统中实现,比如,光学系统、囚禁离子或原子系统等[19,20]。但是目前物理系统中存在损耗等因素导致行走步数受限,因此实际应用需要通过较少的演化步数就能得到最大纠缠态。本文提出演化奇数步和较少的偶数步即可得到最大纠缠态的方案,此纠缠态制备方案更有利于在实际物理系统中的实现。本方案可以推广用于制备单光子、单离子等微观粒子不同自由度之间的纠缠态。
1 理论模型
量子行走包含量子硬币和行走者,其中量子硬币是二维系统,硬币状态|0〉(|1〉)表示行走者向左(右)行走。行走者的状态是|x〉,x∈Z。每一步的幺正演化是

其中I是作用在行走者上的单位算符。Cx是与位置相关的硬币操作,具体表示为

式中:θ∈[0,π/2],φ∈[0,2π]。当行走者处于x=0处,相比较其他x≠0的情况多一个相位因子φ。当φ=0时,硬币操作在所有位置都是相同的。Sx是条件平移算符,具体表示为

它描述的是当硬币状态是|0〉(|1〉)时,行走者向相邻的位置向左(右)移动一个格点。
考虑行走者初始处于原点x=0,量子硬币处于|0〉和|1〉的任意叠加态,整个系统初始状态是

式中:a(0,0)=cosα,b(0,0)=eiβsinα,其中 α ∈ [0,π/2],β ∈ [0,2π]。经过t步演化后,由幺正演化操作(1)式可得到系统的末态
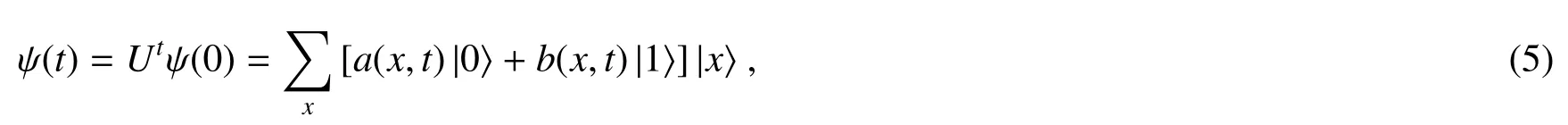
式中x=-t,-t+2,···,t。根据归一化条件,直接得到由硬币-行走者演化后的末态,可以进一步计算两者之间的纠缠度。
2 硬币和行走者之间的纠缠度量
由于初始状态(4)式是纯态,并且整个系统的演化过程是幺正的,因此(5)式描述的硬币-行走者的末态也是纯态。因此,行走者和硬币之间的纠缠度可以通过冯·诺伊曼熵(又称纠缠熵)来度量。纠缠熵的定义可表示为

式中ρc=Trp(|ψ(t)〉〈ψ(t)|)是硬币的密度矩阵,通过对行走者空间坐标求部分迹得到。E=1表示行走者和硬币之间处于最大纠缠关联;E=0表示两者处于可分态,完全没有纠缠关联。(6)式中硬币密度矩阵可表示为


由(8)式很容易看出,硬币与行走者之间的纠缠熵不仅与初始状态有关,还与整个系统的演化操作以及演化步数有关,这一结论和之前类似工作得出的结论相符。将具体讨论(1)式中演化算符的参数θ、φ,(4)式中系统初态系数α、β,以及演化步数或者称为演化时间t对纠缠度[如(8)式所示]的影响。
最大纠缠态的必要不充分条件是硬币密度矩阵的两个对角矩阵元都是0.5[18]。要满足这一条件,首先选择演化操作算符参数θ=π/4以及系统初态系数α=π/4,后续讨论同时改变θ和α得到满足此条件的情况。固定演化步数t=50,计算选取不同的初态系数β,即:初态中|0〉和|1〉有不同的相对位相值,纠缠度随系统演化算符参数φ的变化情况如图1所示。当β=0时,此时初态是纠缠度随φ的变化情况如图1(a)所示,选取合适的φ能够对纠缠度进行优化,但是无法得到最大纠缠态(即纠缠熵为最大值 1)。当 β = π/4 时,即初态为时,纠缠度随φ的变化情况如图1(b)所示。此时,当φ=π/4时,得到的最大纠缠熵E=1,当φ=5π/4时,得到接近最大纠缠的量子态E=0.99。类似地,当β =3π/2、初态是时得到最大纠缠态,φ=3π/4时得到纠缠度为0.99的接近最大纠缠的量子关联。
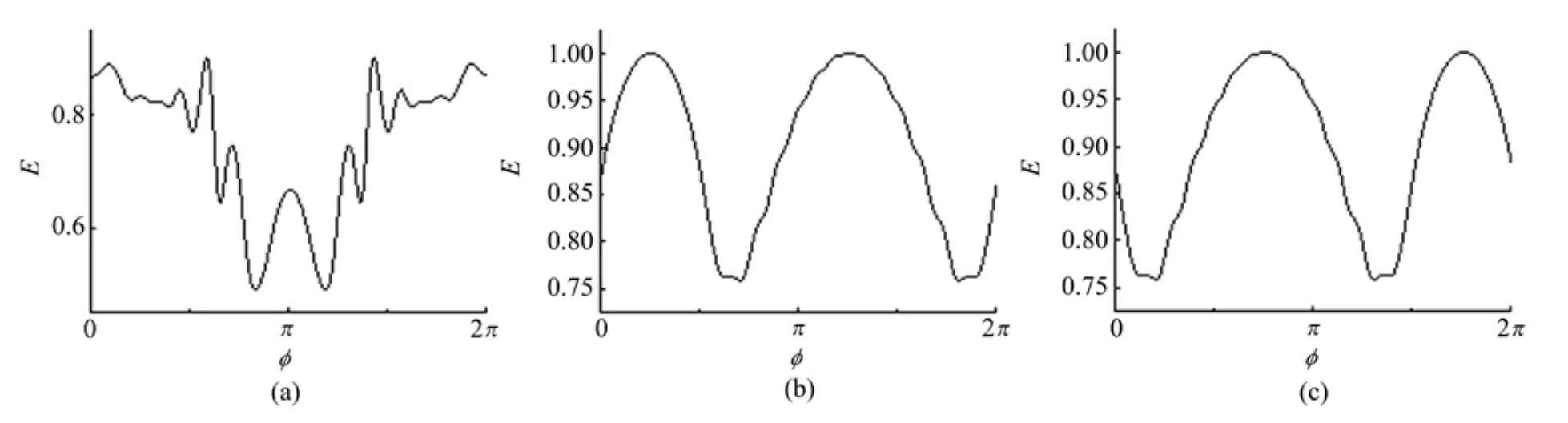
图1 纠缠度随硬币操作位相φ的变化情况,演化操作系数θ=π/4,初态系数α=π/4。(a)β=0;(b)β=π/4;(c)β=3π/2Fig.1 The entanglement entropy as a function of coin operation phase φ with evolution operation coefficient θ= π/4,initial state coefficient α = π/4.(a)β =0;(b)β = π/4;(c)β =3π/2
接下来讨论选定硬币操作系数θ=π/4和演化步数t=50,分析初态以及位相因子φ对纠缠熵的影响。如图2所示,黑色实线对应φ=0、黑色点线对应φ=π/4的情形。先计算β=0,即:初态是时纠缠度随初态叠加系数α的变化情况,如图2(a)所示。当φ=0、α=7π/20,得到接近最大纠缠态E=0.997,但始终无法得到最大纠缠态。进一步考虑初态的相对位相为β=π/2的情形,即:初态是纠缠度随α的变化情况如图2(b)所示。取φ=0时,最大纠缠度为0.867,而取φ=π/4,当α=π/4纠缠度得到最大值1,此时改变α总可以得到纠缠关联大于0.9的纠缠态。进一步展示纠缠度随初态中描述相对位相的参数β的变化情况,如图3所示,此时θ=π/4,α=π/4,t=50,初态的形式是图3(a)中黑色实线对应φ=0、黑色点线对应φ=π/4的情形;图3(b)中黑色实线对应的是φ=π、黑色点线描述的是φ=7π/4的情形。对于等几率幅叠加的初态,当φ=0时,即:演化操作在所有位置都是相同的操作时,纠缠度随初态中相对相位β变化不大并且无法得到最大纠缠态。如果在原点处添加位相,φ=π/4,7π/4时,分别选择β=π/2,3π/2得到最大纠缠态。
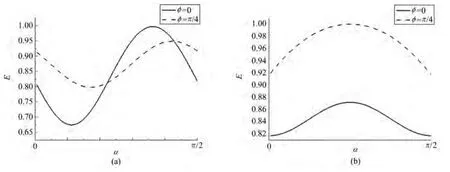
图2 纠缠度随初态系数α的变化情况,θ=π/4。(a)β=0;(b)β=π/2Fig.2 The entanglement entropy as a function of the initial state coefficient α with θ= π/4.(a) β =0;(b)β = π/2
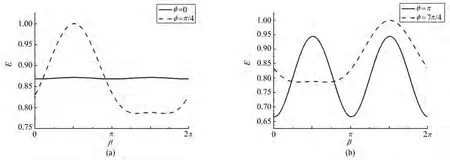
图3 纠缠度随初态系数β的变化情况,θ=π/4,α=π/4Fig.3 The entanglement entropy as a function of the initial state coefficient β with θ= π/4,α = π/4
最后计算纠缠熵随演化时间的变化情况,如图4所示。根据上述讨论,对于固定步数,θ=π/4、α=π/4是导致硬币密度矩阵满足最大纠缠的必要条件。演化操作中参数φ=0时如图4黑色点线和黑色点划线所示,选择所有位置的演化操作都相同,纠缠都随着演化步数的改变在0.8附近振荡,但始终无法达到最大值1。如果在原点处加合适的位相操作因子φ=π/4,再加上合适的初态β=π/4,除了第2步,纠缠度随着演化步数增大而增大并达到最大纠缠,如图4黑色实线所示。而如果选择不同的初态β=0,纠缠度随演化步数的变化依然是振荡的,并无法得到最大纠缠态。
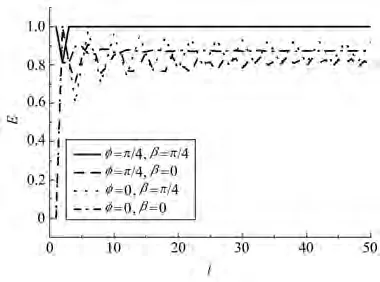
图4 纠缠度随演化时间的变化,θ=π/4,α=π/4Fig.4 The entanglement entropy as a function of evolution time with θ= π/4,α = π/4
3 结论
综上所述,量子行走中硬币和行走者之间的纠缠关联是量子信息处理过程的重要资源。在之前的理论和实验工作中,为了得到最大纠缠态,需要的演化步数高达100步以上才能得到接近最大纠缠的量子态。之前的实验都是通过在量子行走中添加随演化时间完全随机改变的位相,而在所提出随时间不变的有序模型中,量子纠缠度与演化操作、初态以及演化时间都有关。分别计算了纠缠度随量子行走演化操作系数、初始状态系数以及演化时间的变化情况。当所有位置演化操作都相同时,改变系统初态无法得到最大纠缠态。在原点处添加合适的位相操作,再选择合适的系统初态,经过较少步数的演化即可得到高维量子纠缠态。所提出方案为实验实现高维纠缠态调控提供了简单可行且更易于实现的方法。
