基于Cirq的Grover搜索算法的电路实现

吴 希,李志强

(扬州大学信息工程学院,江苏 扬州 225100)

0 引言

Grover量子搜索算法[1]是经典的量子算法之一,体现了量子计算的优势和广阔的应用前景。它利用量子的并行性,将传统计算机的搜索算法从O(N)的复杂度降为,很大程度上提高了搜索效率。然而,Grover算法也存在局限性,当搜索的目标数超过搜索总数的1/4时,搜索的成功率会迅速下降,当目标数超过1/2时,算法就会失效[2]。为了让Grover算法有更多的应用前景,研究人员在算法的改进与优化方面做了大量研究,主要的改进方式有以下三种[3-5]:(1)改变一些步骤或变换算子;(2)改变运算算子的相位旋转角度;(3)寻找更一般的初始态幅值来解决寻找中值、最小值等特定问题。其中,从相位角度的改进效果最好。

当前还没有研制出成熟的量子计算机,所以对量子算法进行模拟实验具有重要意义。Cirq[6]是谷歌发布的一款基于Python的开源框架,用于模拟NISQ(Noisy Intermediate-Scale Quantum)计算机上的电路,使研究人员能在特定的处理器上编写量子算法,解决实际的计算问题,对复杂的细节进行研究。本文通过Cirq框架实现Grover算法的量子电路模拟,根据实验模拟结果验证了Grover算法的正确性,同时也证明了该算法存在的不足。并且介绍了基于改变相位旋转角度的精准算法[7],对算法进行量子电路模拟实现,验证了精准算法的有效性。由此可见,Cirq为量子电路的模拟提供了技术支持,使人们对理论的研究更具现实意义。

1 Grover基本算法实现

1.1 算法步骤和几何描述

假设要在N=2n个无结构的搜索元素中寻找M个目标解,1≤M≤N,找到M中的任意一个解都算成功。于是元素指标可以存储在n个量子比特中[8]。

首先介绍Grover算法中的一个重要操作:Oracle操作。定义一个f(x),x是搜索的元素,当满足f(x)=1,x是搜索问题的解,反之则不是解。在搜索的过程中将注意力放在元素的索引上,搜索范围就是0～2n-1。Oracle是一个能够识别出搜索问题目标解的酉算子,被定义为|x,q〉→|x,q⊕f(x)〉,其中:|x〉存储搜索元素的索引,|q〉是一个单量子比特,⊕表示模2加。把|q〉初始化为|-〉,当f(x)=1时,状态的概率幅进行翻转变成负的;反之则不变。由于在Oracle作用前后|q〉并没有发生变化,所以该操作可以化简为O:|x〉→ (-1)f(x)|x〉。

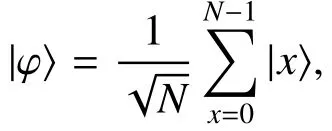
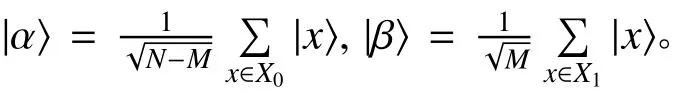
1.2 电路实现

用一个示例来说明Grover算法在2-qubit搜索空间中的具体电路。其中Oracle的相位翻转操作用受控Z门来实现。如图1所示,满足f(x0)=1的四个电路由上至下分别对应x0=0,1,2,3的情况。每个电路的右边给出了对应的真值表,由表可以看出,电路能够实现O:|x〉→(-1)f(x)|x〉的操作。

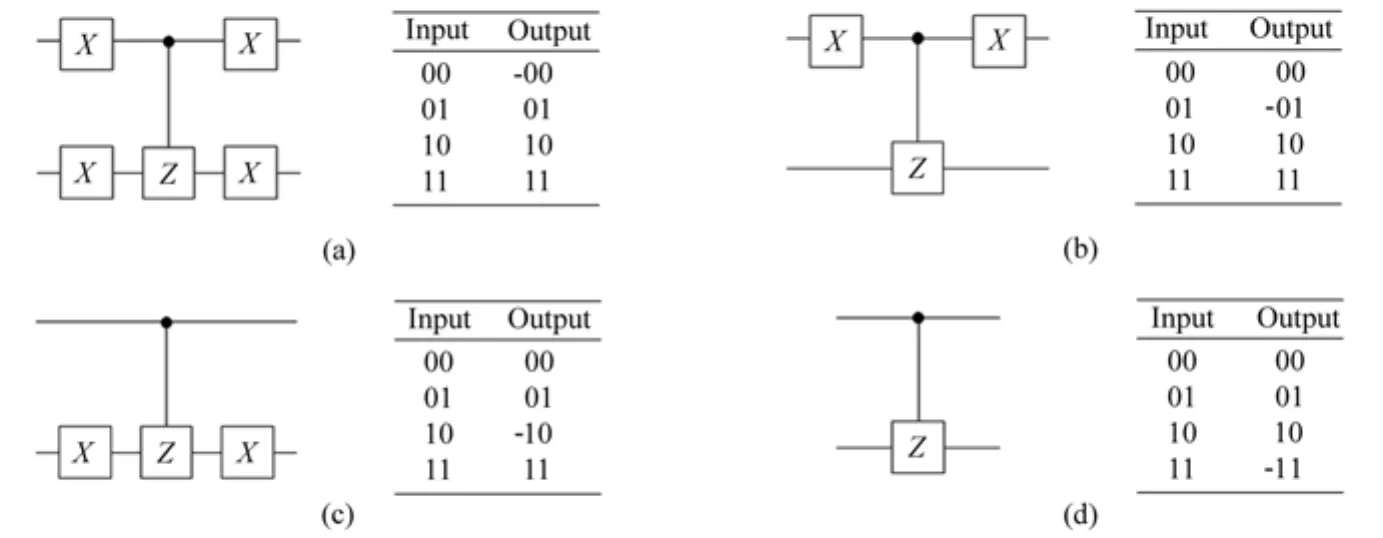
图1 Oracle电路以及目标位(a)00,(b)01,(c)10,(d)11的真值表Fig.1 Oracle circuit and truth table of target bits(a)00,(b)01,(c)10,(d)11

假设目标解是|11〉,那么2-qubit的Grover电路如图2所示,实线框中是|11〉对应的Oracle操作,虚线框中是扩散操作,只需进行一次Grover迭代。

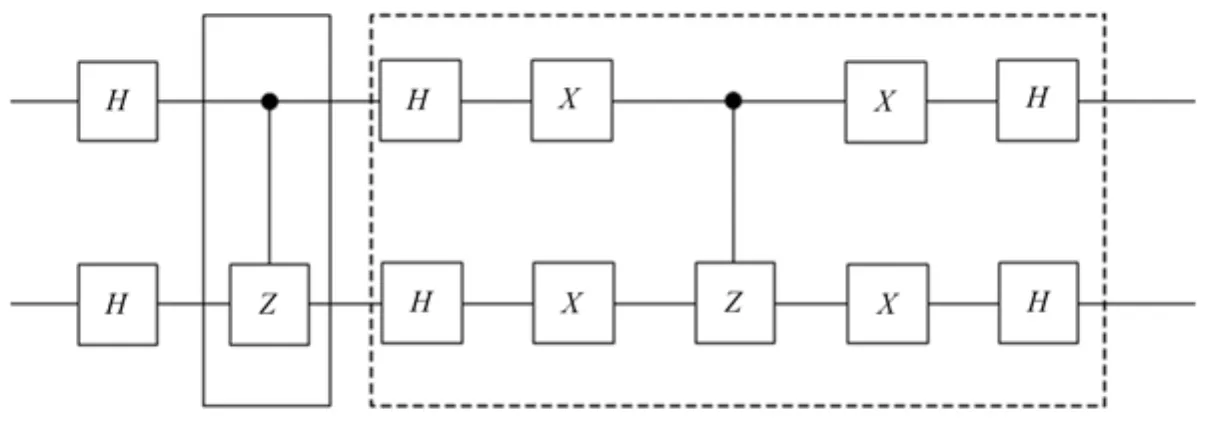
图2 2-qubit的Grover算法电路Fig.2 Circuit of 2-qubit Grover algorithm

将电路扩展至n-qubit,通过基于python3.7的Cirq框架,在联想V3000上实现n-qubit的Grover量子电路,实现的部分代码如下:

import cirq def make-Oracle(q,qn-1,x-bits): ♯Oracle操作yield(cirq.X(q)for(q,bit)in zip(q,x-bits)if not bit)yield cirq.Z(q[len(q)-1]).controlled-by(*qn-1)yield(cirq.X(q)for(q,bit)in zip(q,x-bits)if not bit)def make-Grover(q,qn-1): ♯Grover算子yield cirq.H.on-each(*q)yield cirq.X.on-each(*q)yield cirq.Z(q[len(q)-1]).controlled-by(*qn-1)yield cirq.X.on-each(*q)yield cirq.H.on-each(*q)def main():q=[cirq.GridQubit(i,0)for i in range(n)]♯n位量子比特qn-1=[cirq.GridQubit(i,0)for i in range(n-1)]♯前n-1位量子比特x=random.sample(range(0,2**n),m) ♯随机生成m个目标数count=int((math.pi/4)*(2**n/m)**0.5) ♯迭代次数circuit=cirq.Circuit(cirq.H.on-each(*q)) ♯准备叠加态的电路for-in range(0,count): ♯Grover迭代电路for i in x-bitsM:circuit.append(make-Oracle(q,qn-1,i))circuit.append(make-Grover(q,qn-1))circuit.append(cirq.measure(*q,key=’result’)) ♯测量simulator=cirq.Simulator() ♯模拟器result=simulator.run(circuit,repetitions=100000) ♯测量结果

1.3 实验结果及分析

对电路进行测试,输入3位量子位数和1个目标元素,对电路进行100000次测量,对测量结果进行采样。运行结果如图3所示,电路图中第一个虚线框是Oracle操作,第二个框是扩散操作,进行了两次Grover迭代。随机产生的一个目标元素是5,采样结果根据次数由高到低显示,测量得到5的次数最多,为94519次;测量到其他数的次数在800左右。根据结果可知算法正确的概率大约为94.5%。

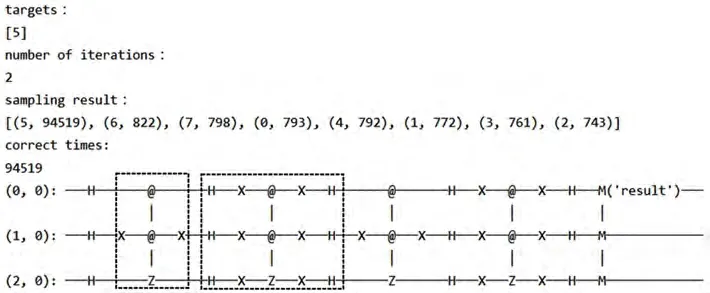
图3 3-qubit的实验结果Fig.3 Experimental results of 3-qubit

对目标数占搜索总数的1/2这一情况进行实验,测试结果如表1所示。时刻表示所有在同一抽象时间段内执行的操作的集合。例如图3的三个用于初始化的H门表示一个时刻数。从表1可以看出,当目标元素为总搜索数的1/2时,不论数量有多大,搜索的成功率都为50%。当运行到13个量子位时,输出的电路会出现错误,原因是电路的复杂度达到上限,但测量得到的结果是准确的。若将13个量子位的目标数改为2048,则可以输出正确的电路,说明Oracle查询的复杂度对电路复杂度的影响很大。目标数成倍增加伴随着Oracle查询越复杂,所需时刻数与门数也趋于成倍增加,运行时间也就越长。

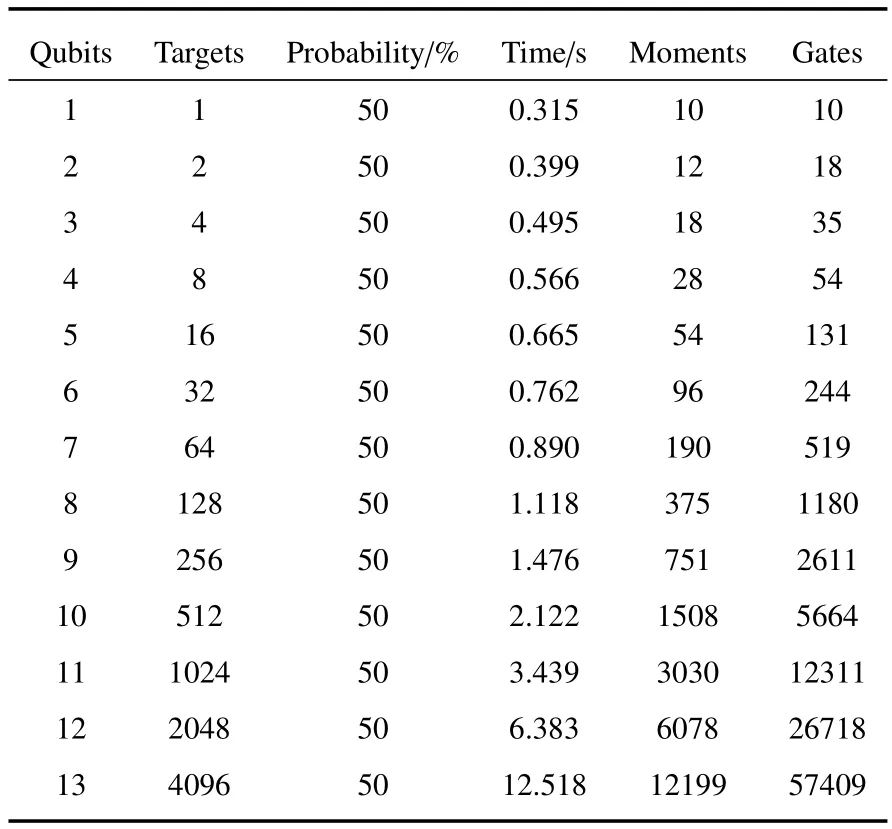
表1 目标数为1/2时的实验结果Table 1 Experimental results when the number of targets accounted for 1/2 of the total

以固定的1024个搜索总数为例验证算法的性能,实验结果记录在表2中。随机生成无序的搜索目标并且不断增大目标元素的数量,分析目标元素与搜索总数的比值λ对Grover迭代次数R以及搜索成功概率P的影响。

表2 Grover算法成功率实验结果Table 2 Experimental results of the success probability rate of Grover algorithm

从表2可以看出,当0.3＜λ＜0.5时,算法的成功率迅速下降,迭代的次数始终是1;当λ＞0.5时,算法的成功率甚至低于失败率。传统的搜索方法是目标元素越多,成功率则越高,而量子Grover算法却是在搜索数较少时有较高的成功率。除此以外,传统的搜索方法总能得到百分百的正确率,基本Grover算法由于其测量特性,可能需要进行多次搜索才能达到预期效果。

2 精准Grover算法的实现

上文介绍了Grover量子搜索算法的基本步骤、几何描述以及公式推导。也通过在Cirq框架上对电路的模拟分析,直观地了解到Grover算法存在的局限性。已有许多学者针对这些不足进行了深入研究。Long等[9]最初发现Grover算法中的两个相移算子可以被相位匹配关系的相位角代替,基本的Grover算法中存在两次相位翻转,翻转的角度都是固定的π。目前,基于两个旋转算子中旋转相位匹配条件的改进,提出了许多可以提高搜索成功概率的改进算法[10-12]。通过Cirq框架可以很容易地模拟这些改进算法。

Long等[9]首次提出了精准的量子搜索算法,使搜索的成功率达到100%。但该算法存在两个缺陷,一是只适用于搜索一个目标元素,二是无法解决目标数占总搜索数1/2的情况。所以Xia等[8]在此基础上进行改进,先将相位取反,再将搜索总数这一变量引入到相位旋转角度中,使得算法具有实时性,成功概率一直为100%。这一算法非常适合需要高精度的应用场景中的搜索。该算法将相位旋转角改为

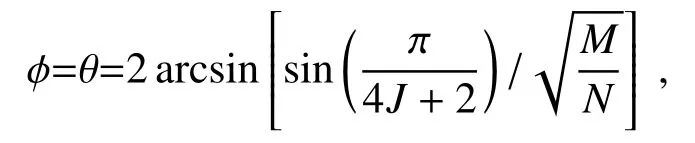
通过基于google的Cirq框架模拟实现精准算法,只需要在基本的Grover算法中添加旋转角度这一变量,部分代码如下:

♯根据公式算出相位旋转角度angle和迭代次数count a=(m/2**n)**0.5 bl=2*math.asin(a)J=(math.pi-bl)/(2*bl)count=math.ceil(J)t=math.sin(math.pi/(4*count+2))/a angle=2*math.asin(t)/math.pi♯为旋转Z门添加旋转角度yield Cirq.Z(q[len(q)-1]).controlled-by(*qn-1)**angle

对3-qubit精准算法进行测试,随机产生三个目标元素,单次运行结果如图4所示,测量正确的概率为100%,并给出了旋转门所需旋转的角度为0.608。电路图中的第一个虚线框对应三个目标元素的Oracle操作。

经过多次实验,模拟实现的结果与理论计算结果一致,算法的成功率始终是100%,验证了算法的有效性。用Cirq框架可以轻易地模拟出基于相位旋转匹配改进算法的电路。相比于文献[13]中使用量子程序设计语言QCL模拟实现,使用Cirq框架实现量子算法,不仅能够看到概率性以及复数矩阵的输出,还能看到整个算法实现的完整电路,这对电路的优化起到了很大的帮助。

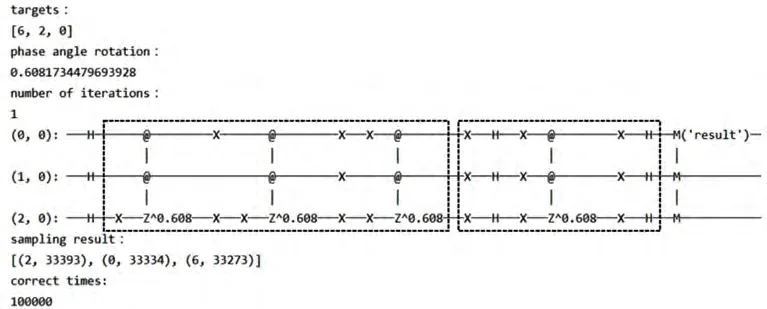
图4 3-qubit精准Grover算法的结果Fig.4 Results of 3-qubit accurate Grover algorithm

3 总结与展望

借助Cirq框架,对基本Grover算法及其改进的精准算法进行了电路模拟,对测试结果进行分析,验证各算法的准确性以及各自存在的特点,方便应用于不同的情景。搜索算法的相位旋转通过改变旋转Z门的角度来实现,但目前只是对其进行模拟,还未在特定的处理器上实现,而Cirq也提供了在实际硬件上运行的功能,以便未来开展进一步的优化工作。本研究中基于相位旋转匹配的改进算法都是在目标分量已知的情况下,算法的迭代次数都依赖于目标分量的数量。当目标分量的数量未知时,往往需要很高的Oracle查询复杂度,而且如何在最优迭代次数时停止也是需要研究的问题。已有一些改进的算法来解决这一问题[14,15],但在效率与概率方面都存在进步空间,希望未来能够在目标分量未知的情况下,通过Cirq框架对算法进行优化、验证与分析。此外,通过对Cirq框架源码的深入理解,还可以更多地扩展其功能,为电路的模拟提供更强大的技术支持。