宽谱段Czerny-Turner光谱仪设计
2022-06-10李世文郑小兵翟文超
李世文,郑小兵,翟文超*
(1中国科学技术大学环境科学与光电技术学院,安徽 合肥 230026;2中国科学院合肥物质科学研究院安徽光学精密机械研究所通用光学定标与表征技术重点实验室,安徽 合肥 230031)
0 引言
成像光谱仪能够在连续光谱段上对同一目标同时成像,可直接反映出被观测物体的光谱特征,因此可用于环境污染管理、城市规划、土地资源分析、地质与矿产调查、大气探测等领域[1,2]。色散系统是光谱仪核心部分,直接影响光谱仪的性能和大小[1-5]。传统的Czerny-Turner结构通常用于单色仪和辐照度仪,使用单元探测器[6]。由于单元探测器的光敏面通常远大于光谱展宽,不需要校正像散,并且通过转动光栅来输出不同波长的光,因此只需校正中心波长像差[6]。当使用线阵探测器时,需要在连续光谱段上对同一目标同时成像,探测器尺寸通常只有十几微米,像散会严重影响光谱仪分辨率,且光栅固定,需要在宽谱段范围校正像散。像散是影响宽波段Czerny-Turner光谱仪的主要像差[7]。
Xue等[8]提出校正了540~780 nm波段范围内全像散的方法,但是此方法只能校正中心波长及附近的像散,对于更宽的波段范围不能起到良好的校正作用。目前Czerny-Turner结构光谱仪应用较成熟,但对于整个近红外波段的像散校正方面的研究很少[9]。本文通过光栅产生的像散补偿球面反射镜的像散来校正中心波长的像散,再通过柱面镜的像散补偿边缘波段的像散,之后通过MATLAB计算Czerny-Turner光谱仪初始结构值。通过准直光路连接两个Czerny-Turner光谱仪,从而实现了波段范围在900~2500 nm的消像散Czerny-Turner光谱仪成像系统。
1 零阶消像散条件
传统的Czerny-Turner光谱仪结构如图1所示,复色光从狭缝入射到Czerny-Turner光谱仪,通过准直镜入射到光栅,经过光栅色散将复色光分解成单色光之后入射到聚焦镜,聚焦到探测器上,形成一列按照波长排列的单色光谱[10]。
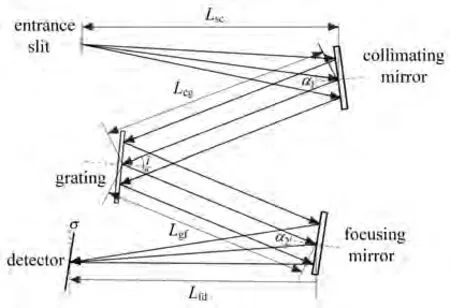
图1 Czerny-Turner光谱仪基本结构Fig.1 Basic structure of Czerny-Turner spectrometer
像散是影响宽波段Czerny-Turner光谱仪的主要像差,光线离轴入射导致球面反射镜形成像散,即子午面和弧矢面聚焦能力不同。像散原理图如图2所示,在子午面像点处,弧矢面还未聚焦,因此在子午像面处弧矢面光线形成一个垂直于子午面的短线;在弧矢面像点处,子午面光线在之前已经聚焦,因此子午面光线在弧矢像面处形成一条垂直于弧矢面的短线[11]。在子午像面和弧矢像面之间的像为椭圆形,子午像面到弧矢像面中点为中心焦点,即为弥散斑,会影响光谱仪成像质量和分辨率。
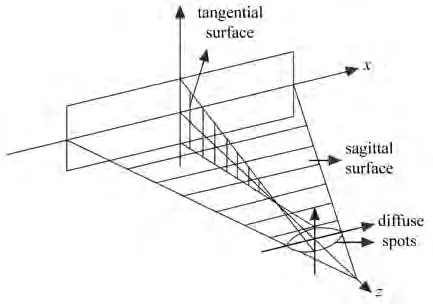
图2 像散原理图Fig.2 Schematic diagram of astigmatism
球面反射镜离轴角为α,物距为l,则它在子午面和弧矢面的像距分别为[12]

对于反射光栅来说,子午面(色散面)满足光栅方程d(sini+sinθ)=mλ(其中:d为光栅常数,i、θ分别为光栅的入射角和衍射角,m为衍射级次,λ为波长)。在弧矢面,反射光栅满足普通反射镜规律。因此,光经过反射光栅弧矢面和子午面的像距分别为

两式联立即可求出聚焦镜到探测器的子午面和弧矢面距离分别为
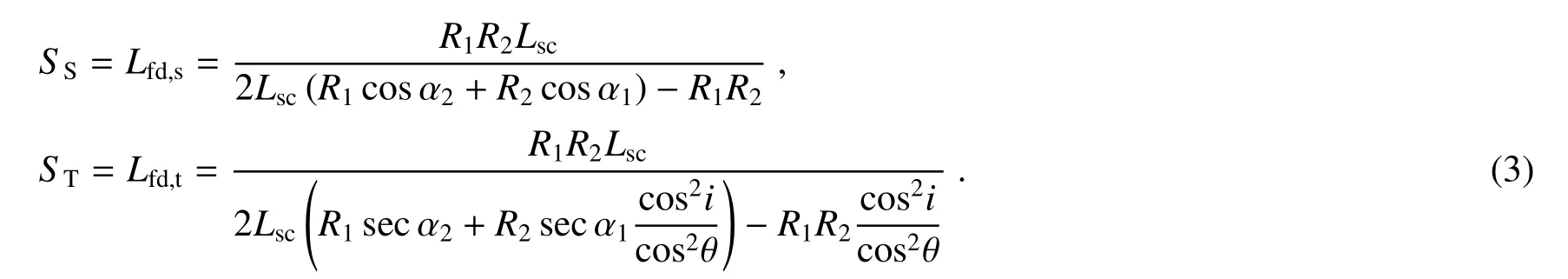
为了校正像散,需要子午像距和弧矢像距相等,SS=ST,即零阶消像散条件,可求出狭缝到准直镜的距离
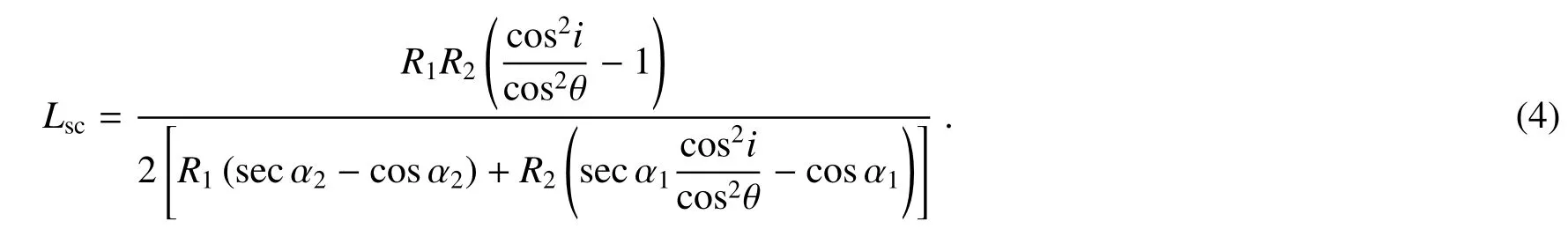
满足零阶消像散条件只能消除中心波长的像散,不能满足边缘波长消像散条件,还需进行一阶消像散。
2 一阶消像散条件
由光栅方程可知,光线沿同一入射角i入射到光栅,不同波长的光衍射角θ不同。θ的变化影响聚焦镜的离轴角α2,进而会影响弧矢面像距SS、子午像距ST和聚焦镜到探测器的距离Lfd的值。要校正宽波段像散,必须使SS、ST和Lfd随θ的变化值相等,即SS、ST和Lfd对θ的一阶导数值相同[13],可表示为

式中


SS、ST分别对α2求偏导,即
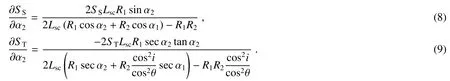
ST对θ求偏导,即
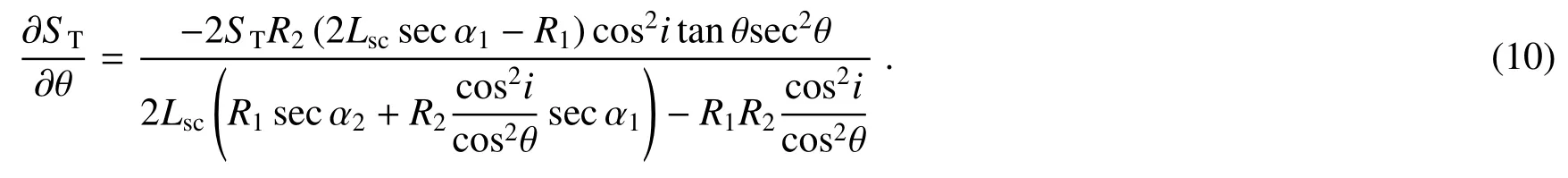
图3为不同波长光线通过光栅衍射后的光路图,C2是聚焦镜F的曲率中心,光线A-O-B是中心波长光线,光线A-O′-B′是边缘波长光线,两光线在探测器上的距离为p,探测器倾角σ。在yAz(光栅色散面)坐标系中,y和z分别表示沿y轴和z轴的单位矢量。
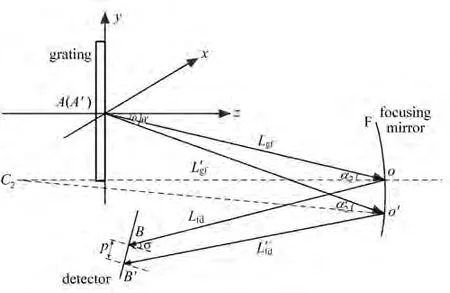
图3 不同波长光线通过光栅衍射后的光路图Fig.3 Optical path diagram of light with different wavelengths diffracted by grating
根据AO+OC2+C2O′+O′A=0可列出矢量AO、OC2、C2O′、O′A的表达式,将矢量表达式代入等式可得
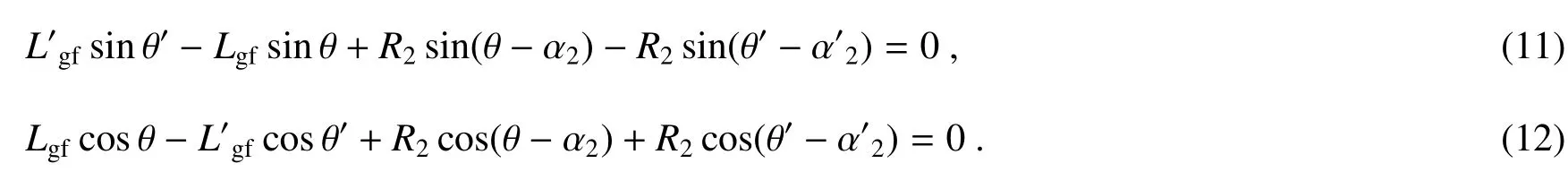
分别对θ′微分,则
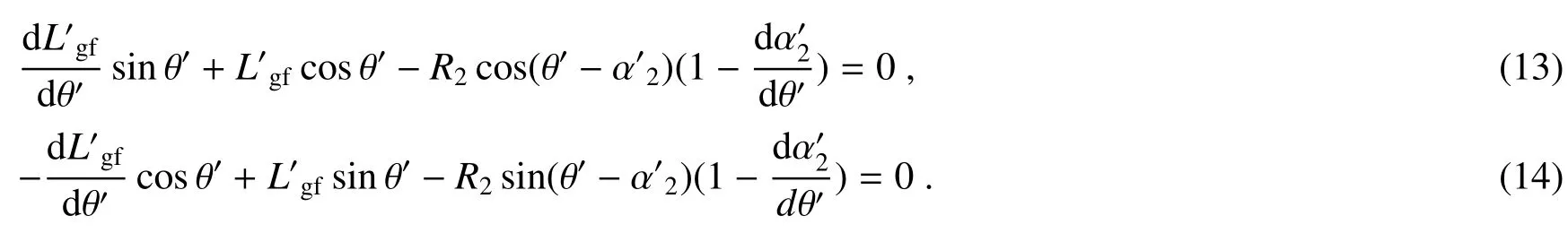
联立(13)、(14)式可解出

联立 (6)~(10)、(15)式可得

(11)式乘以co sθ′,(12)式乘以sinθ′,联立后可解出边缘波长入射聚焦镜的入射角α′2,即

根据C2O+OB+BB′+B′O′+O′C2=0 可列出矢量C2O、OB、BB′、B′O′、O′C2的表达式,将矢量表达式代入等式后对θ′微分可得
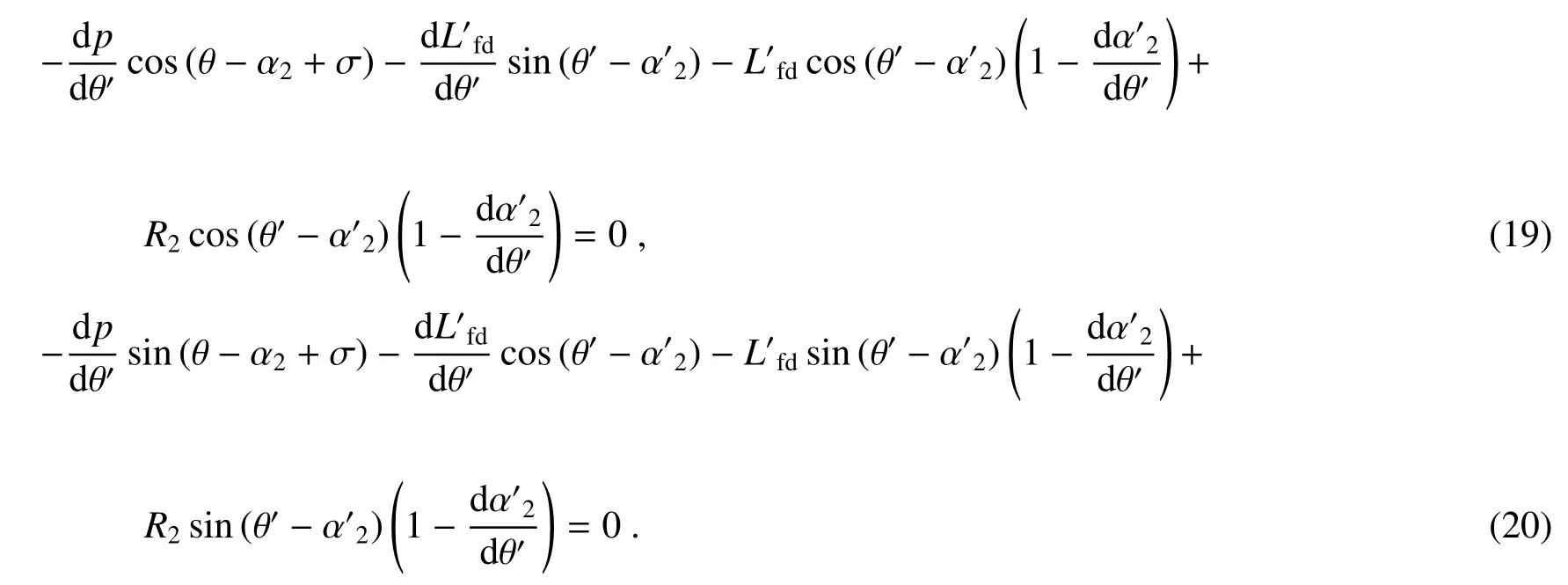
联立(15)、(19)、(20)式可解出
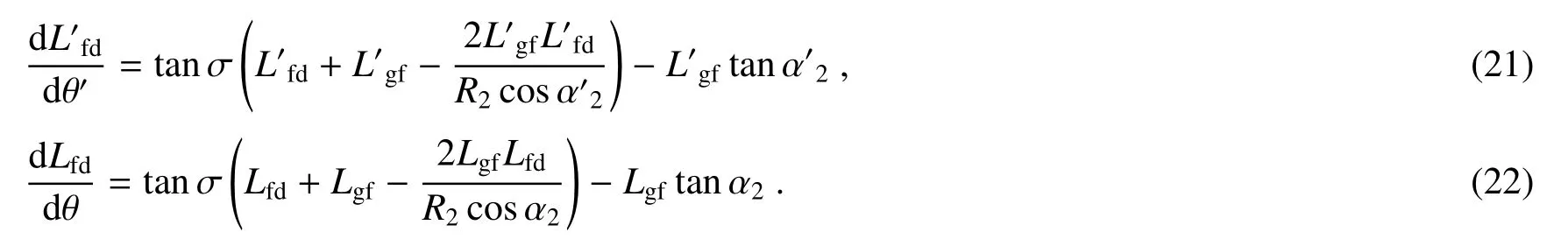
联立(5)、(16)、(17)、(22)式可解出探测器倾角σ,即
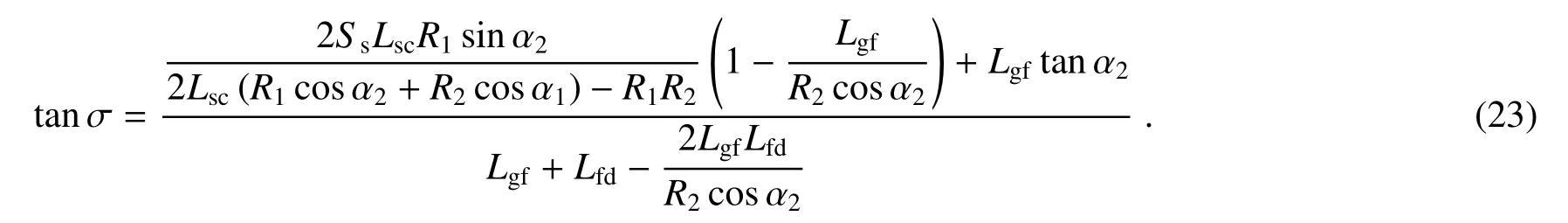
联立(3)、(18)式可解得不同波长的像散值为
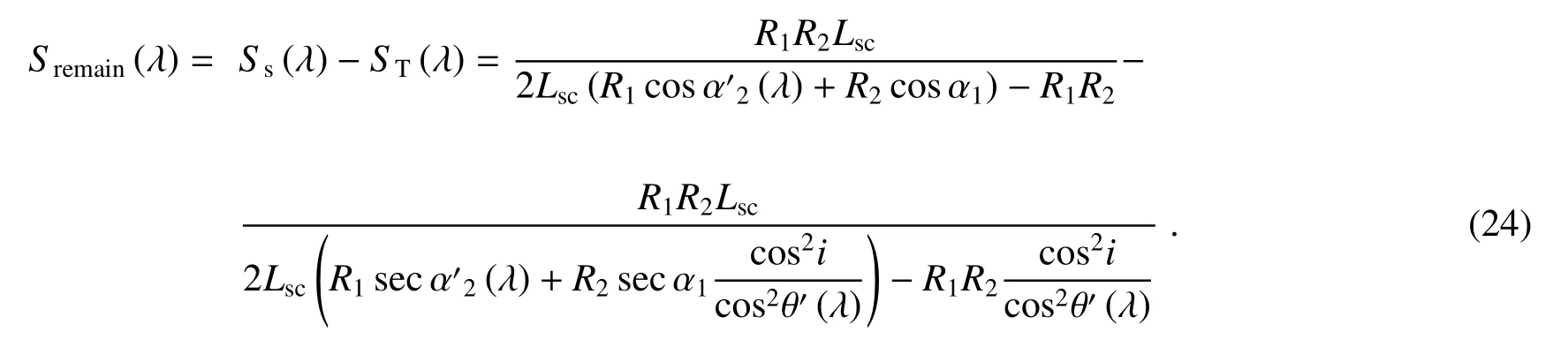
3 柱镜补偿剩余像散
图4为柱镜分别补偿子午面和弧矢面的示意图,柱镜放置在探测器和聚焦镜之间,通过放置一定的倾角γ和柱镜到探测器的距离Lc实现剩余像散的校正。柱镜的子午面相当于平行平板,弧矢面相当于凸透镜。在子午面,光经过平行平板不改变其传播方向,但会改变轴向距离,轴向距离位移量为ΔLt,柱镜在弧矢面形成的位移量为ΔLs,可分别表示为[14]
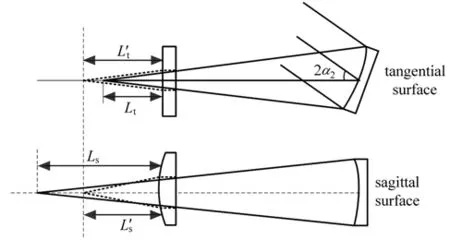
图4 柱镜示意图Fig.4 Schematic diagram of cylinder

式中:n为柱镜折射率,t为柱镜厚度,fc为柱镜焦距。
子午方向的位移量ΔLt和弧矢方向位移量ΔLs的差值即为柱镜像散Scylinder,可表示为

Scylinder>0,柱镜子午面位移量大于弧矢面位移量;Scylinder<0,柱镜子午面位移量小于弧矢面位移量;Scylinder=0,柱镜子午面位移量等于弧矢面位移量,可以用柱镜引入相反像散来抵消Czerny-Turner结构光谱仪球面反射镜的像散。在发散光路中引用柱镜,不会对之前光学系统的距离和倾角有影响,只会在一阶像散校正基础上,再通过柱镜像散的反向校正,从而达到校正宽波段像散的要求。
一阶消像散条件下,中心波长处的剩余像散为0,即Scylinder=0,确定了柱镜的厚度t、折射率n、焦距fc之后,即可确定柱镜到探测器的距离Lc。
为了使剩余像散和柱镜像散不受波长的影响,与一阶消像散相同,选择对波长λ微分,即

式中:H为边缘光线和主光线在柱镜上的距离;dScylinder/dLc可由(27)式微分得到,即

dLc/dH可由几何关系得到,即

dH/dλ可由线色散公式得到,即

dSremain/dα2可由 (8)、(9)式联立得到,即
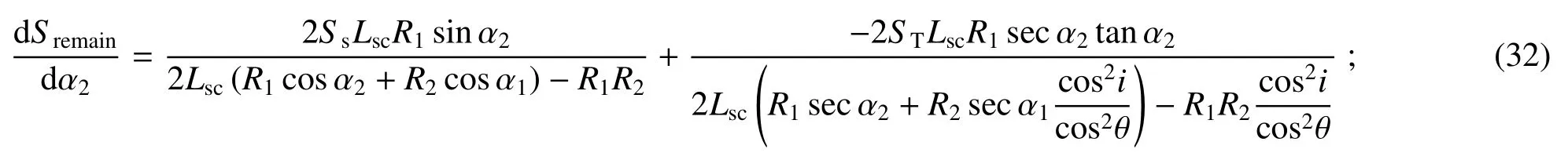

将 (16)、(29)~(33)式代入 (28)式可得
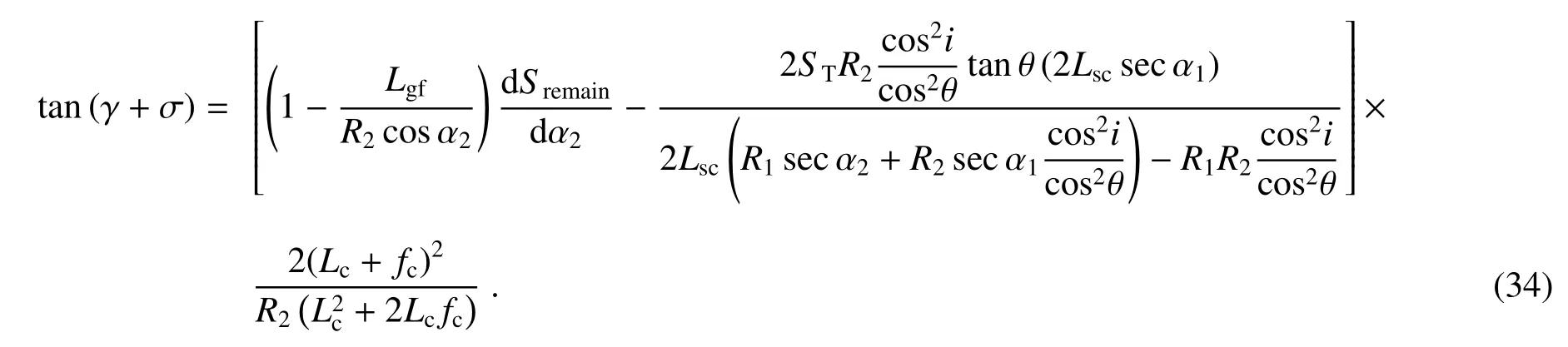
由(27)式可知,当柱镜固定参数(即Lc、n、t)不变时,影响柱镜像散的因素只有距探测器的距离Lc。而边缘波段的值由柱镜倾角决定,如图5柱镜两种摆放方式可知,由于Lc直接影响柱镜的像散值,所以选择合适的柱镜摆放角度很重要。
图5是柱镜摆放位置的两种选择,波长位置从上到下依次减小,图5(a)是长波段小于短波段图5(b)相反。
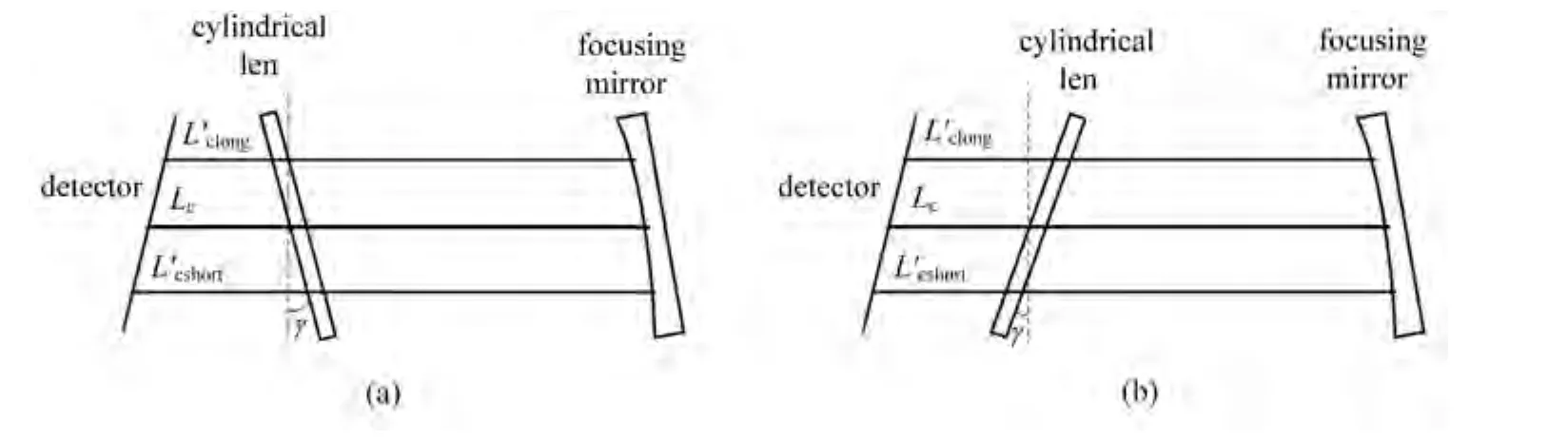
图5 柱镜摆放位置。Fig.5 Different positions of the cylinder.
当n=1.46,t=2 mm,fc=50 mm时,柱镜补偿像散与Lc的关系如图6。
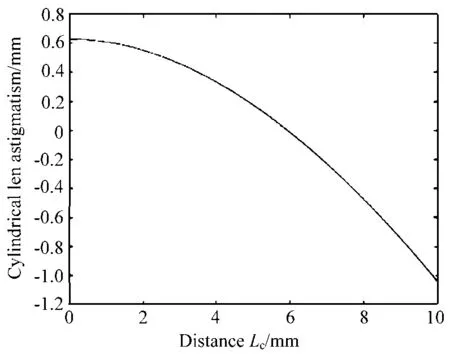
图6 柱镜补偿像散与柱镜和探测器距离Lc的关系Fig.6 Dependence of cylindrical lens compensation astigmatism on the distance between the cylindrical lens and the detector
4 设计与实现
前置光路使用两个离轴抛物面反射镜,将入射狭缝成像到色散单元。反射式系统无色差,离轴抛物面镜可以校正球差[11]。平行光入射到离轴抛物面镜,之后汇聚到焦点。
前置光路使900~1700 nm和1700~2500 nm两个部分连接在一起,使用二向色镜将两个波段分隔开。设置离轴抛物面镜曲率半径R=120 mm,离轴距d=20 mm。为了和后方色散光路耦合,设置像方空间F数为7。前置光路设计如图7所示。
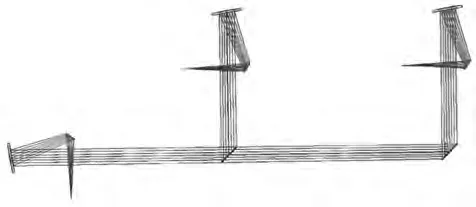
图7 前置光路Fig.7 Front light path
在视场和光瞳各选一点,可以唯一确定一条光线。通过Zemax宏编程功能,随机选定归一化的瞳面(px、py)和视场(hx、hy)坐标,每个设定波长循环1000次,绘出像面光斑图。前置光路像面处的光斑情况如图8所示,因此,与前置光路相接的后方色散光路的入射狭缝设置为75µm×252µm。
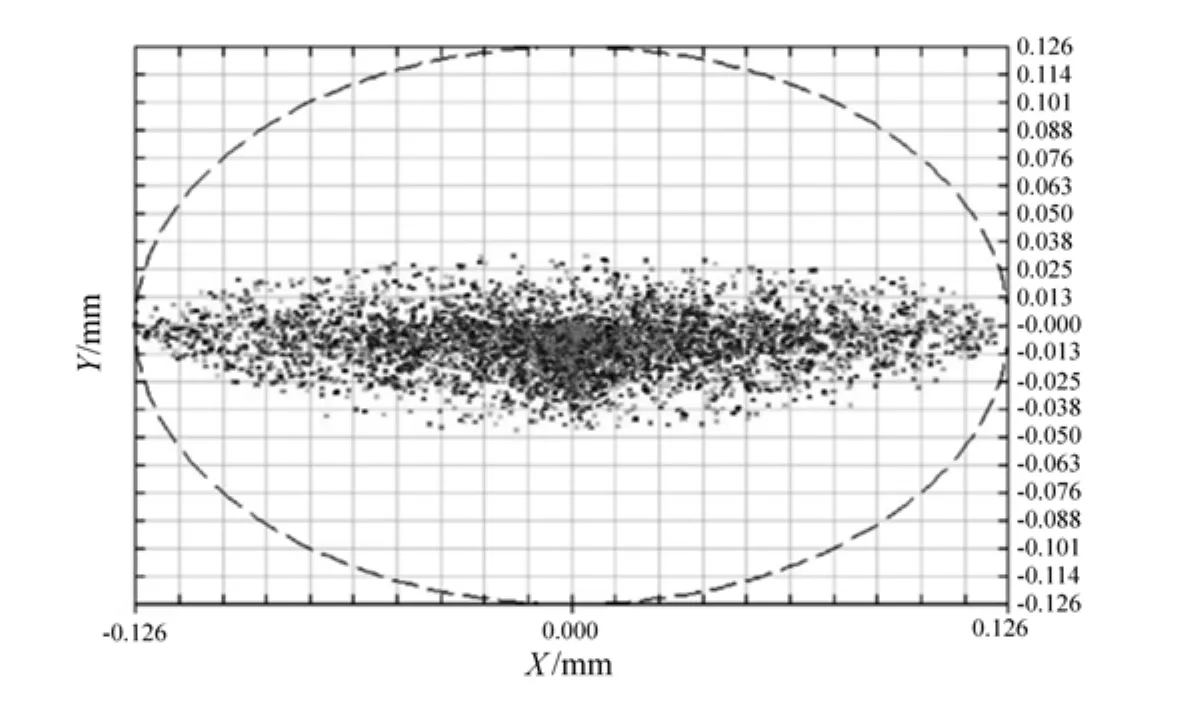
图8 前置光路像面Fig.8 Image surface of front optical path
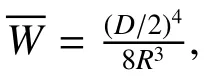
准直镜和聚焦镜是离轴使用,不满足等晕成像条件,因此存在离轴彗差,彗差会使谱线轮廓增宽,影响光谱分辨率,校正彗差需满足Shafer等式[15,16]
基于营口港所需的英语人才现状展开调研,探讨如何改革现有的大学英语教学模式,即如何将公共英语教学与学生所学专业相结合,建立与专业相结合的大学英语教学模式。

光谱仪的狭缝在探测器上成像,狭缝宽度为a,狭缝像宽度为α′,f2为聚焦镜焦距,衍射级次为1。在探测器上,同一波长光分开角度为

根据角色散公式dθ/dλ=m/(dcosθ)可得两条谱线分开的距离

衍射光栅并不是1:1成像,狭缝像的宽度α′与狭缝宽度α、光学系统放大率f2/f1、光栅角放大率γ=cosθ/cosi有关,因此狭缝经光栅成像的像大小为

将(38)式代入(37)式中,可得狭缝像的几何宽度对应的光谱带宽为

狭缝尺寸为75µm×252µm,光谱仪需要分辨率为不大于10 nm,根据(39)式,Δλ≤10 nm,因此,对于900~1700 nm波段,光栅常数d=300 lp/mm,则f1≥25 mm;对于1700~2500 nm波段,光栅常数d=150 lp/mm,则f1≥50 mm。计算初始结构必须首先确保光线、光学器件不能互相干涉,同时要保证机械装调的可能性[17]。
900~1700nm和1700~2500 nm的波长间隔都是800 nm,谱线在像面上分开的距离为l,则
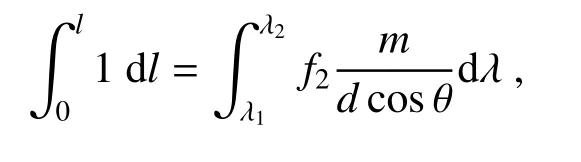

式中θ为中心波长衍射角。使用的探测器尺寸为12.8 mm×0.25 mm,l小于探测器的有效长度,即l< 12.8 mm,根据(40)式,f2≤ 53.33 mm。
900~1700nm波段准直镜入射角α1=5°,根据(35)式,聚焦镜入射角α2=8.61°。初始数据如表1所示。

表1 900~1700 nm波段Czerny-Turner光谱仪初始数据Table 1 Initial data of Czerny-Turner spectrometer in the band of 900-1700 nm
根据第2节一阶消像散计算公式,可以绘出不加柱面镜像散校正情况;根据第3节柱镜补偿剩余像散计算公式,可以绘出加上柱面镜像散校正情况。图9(a)为不加柱面镜的像散随波长变化曲线,可以看出中心波长附近的像散得到较好的抑制,边缘波段像散抑制能力较弱。在900~1300 nm范围内,SS>ST;在1300~1700 nm范围内,SS<ST;仅仅依靠一阶消像散不能有效抑制全波段的像散,必须借助柱镜补偿像散的方法[14]。由图9(b)可以看出加上柱面镜后边缘波长光线的像散得到了明显的抑制。
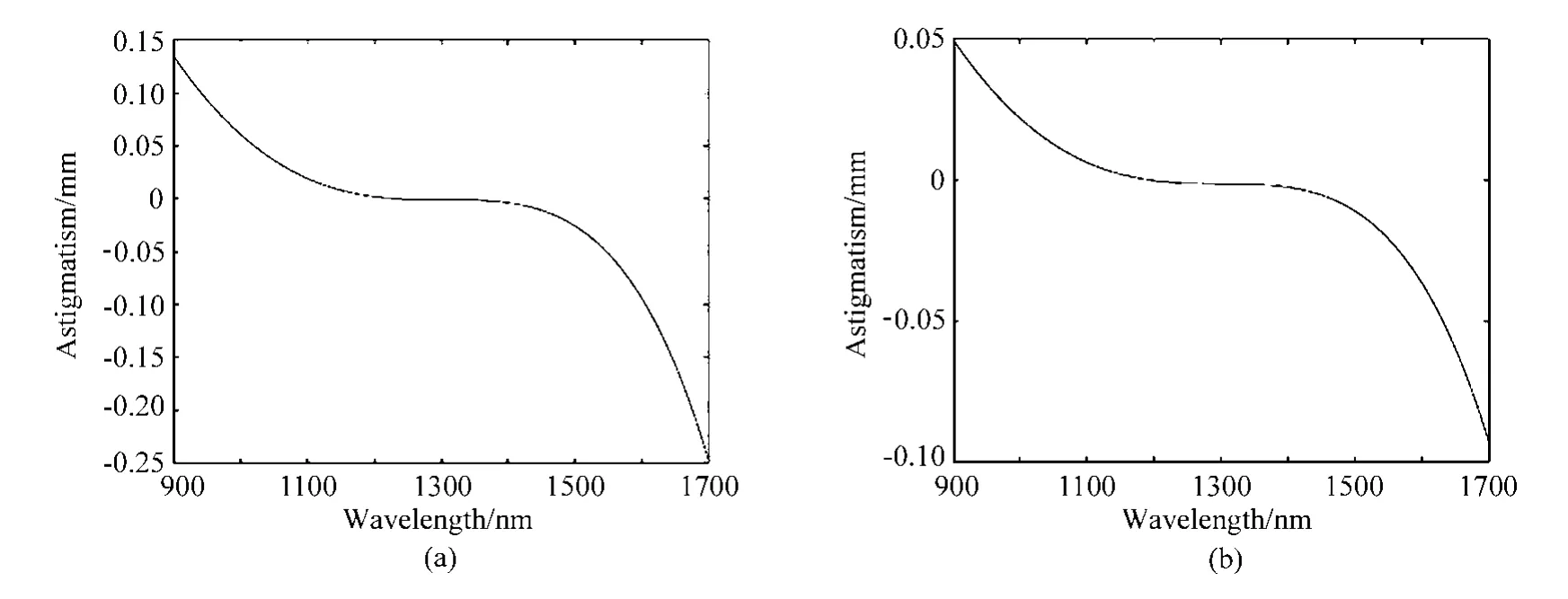
图9 像散随波长的变化曲线。(a)不加柱面镜;(b)加柱面镜Fig.9 Variation of astigmatism versus wavelength.(a)Without cylindrical mirror;(b)With cylindrical mirror
另外,由图9(a)可见,在900~1300 nm波段范围内,SS>ST,即一阶消像散剩余像散Sremain>0,则需要柱面镜像散Scylinder>0;在1300~1700 nm波段范围内,SS<ST,即Sremain<0,则需要柱面镜像散Scylinder<0。第3节图5表示了柱镜摆放位置所需条件,则对于900~1700 nm波段范围来说,选图5(a)中的摆放方式,即柱面镜倾斜方向与像面相反。
图10为900~1700 nm波段Czerny-Turner光谱仪光路图。图11为900~1700 nm全波段RMS与波长关系图,可以看出,在全波段范围内RMS的值均小于4µm,像散得到了很好的抑制。图12为像面光迹图,波长差10 nm的两波长可以分辨,分辨率达到要求。
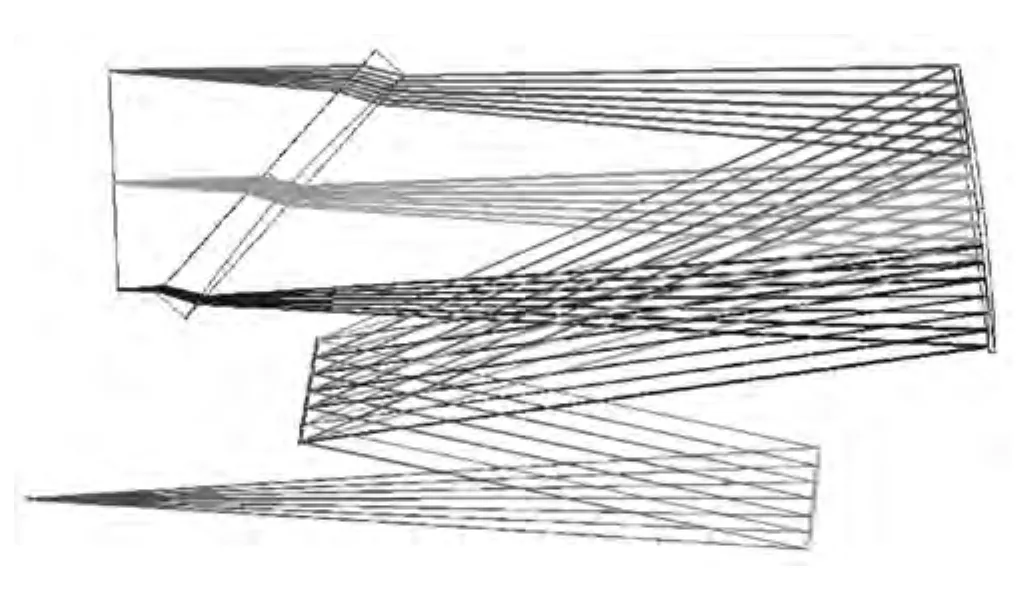
图10 900~1700 nm波段Czerny-Turner光谱仪光路Fig.10 Optical path of Czerny-Turner spectrometer in the band of 900-1700 nm
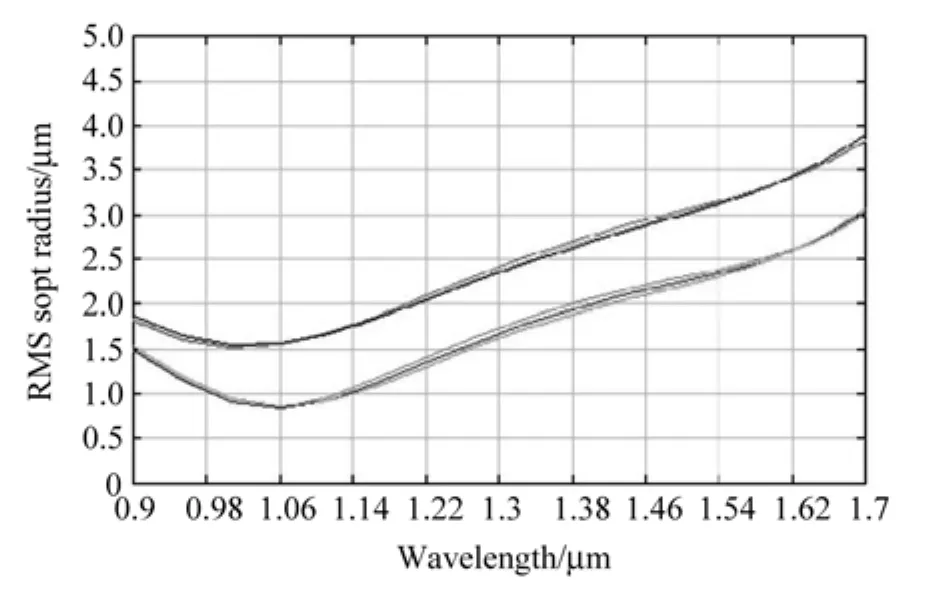
图11 900~1700 nm RMS点半径随波长变化图像Fig.11 Variation of the RMS point radius versus wavelength in the band of 900-1700 nm
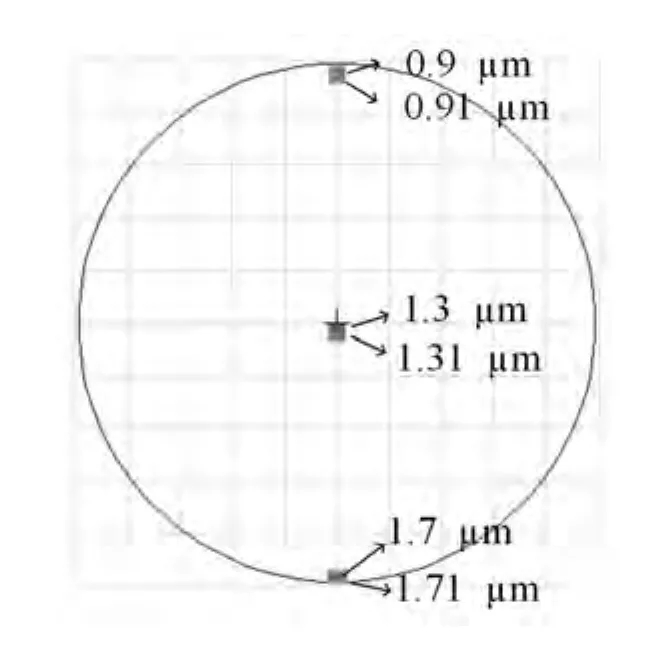
图12 900~1700 nm像面光迹图Fig.12 Image surface light trace in the band of 900-1700 nm
1700~2500 nm波段准直镜入射角α1=6°,根据(35)式,聚焦镜入射角α2=5.3°。初始数据如表2所示。
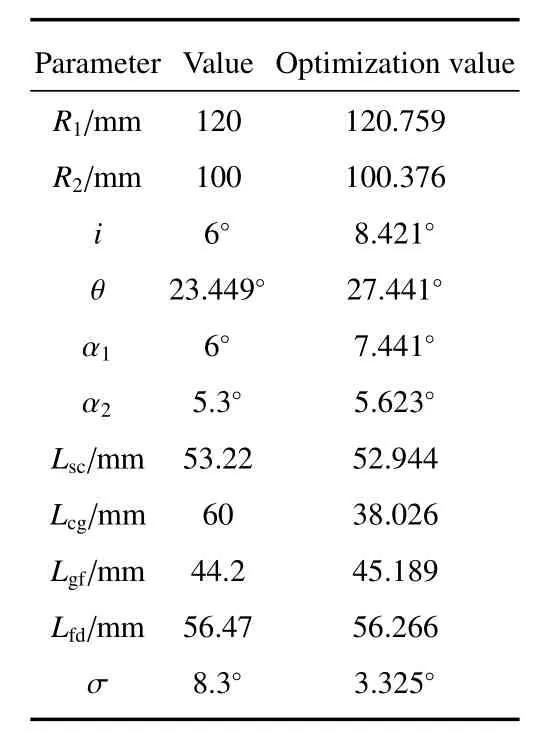
表2 1700~2500 nm波段Czerny-Turner光谱仪初始数据Table 2 Initial data of Czerny-Turner spectrometer with wavelength in the band of 1700-2500 nm
根据第2节一阶消像散计算公式,可以绘出不加柱面镜像散校正情况,图13即为像散值随波长的变化。在1700~2500 nm波段范围内,SS>ST,即全程Sremian>0,此时不适合用柱镜消像散。
图14为1700~2500 nm波段Czerny-Turner光谱仪光路图,图15为全波段RMS与波长关系图,可以看出,在全波段范围内,RMS的值均小于3µm,像散得到了很好的抑制。图16为像面光迹图,波长差10 nm的两波长可以分辨,分辨率达到要求。
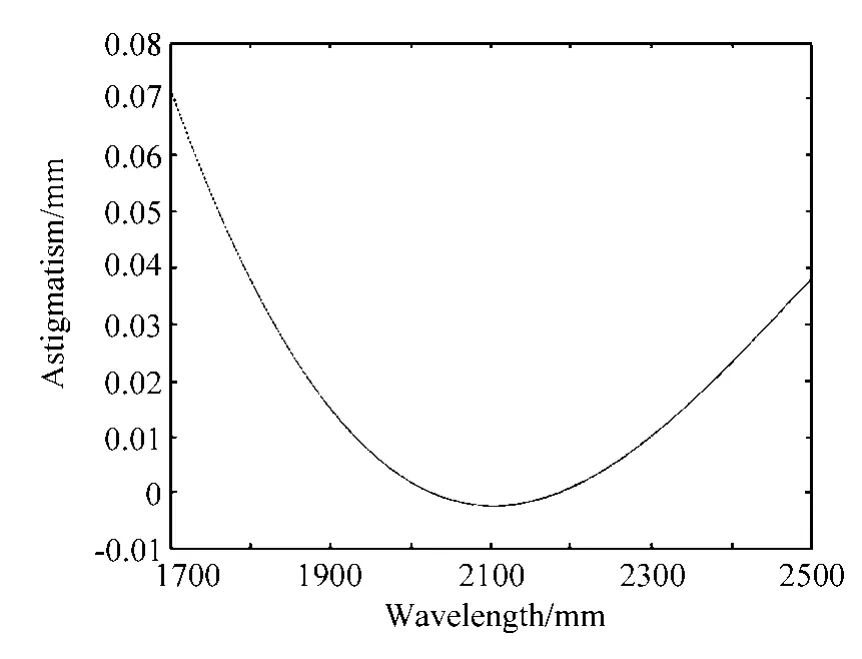
图13 1700~2500 nm像散随波长的变化关系Fig.13 Astigmatism versus wavelength in the band of 1700-2500 nm

图14 1700~2500 nm波段Czerny-Turner光谱仪光路Fig.14 Optical path of Czerny-Turner spectrometer with the wavelength in the band of 1700-2500 nm
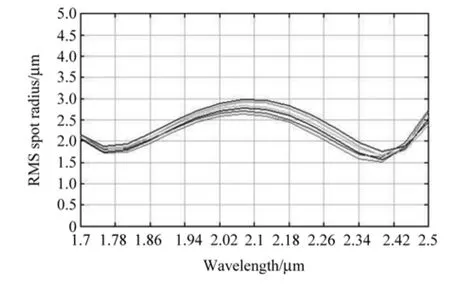
图15 1700~2500 nm全波段RMS点半径随波长的变化Fig.15 Variation of RMS point radius with wavelength in the full band of 1700-2500 nm
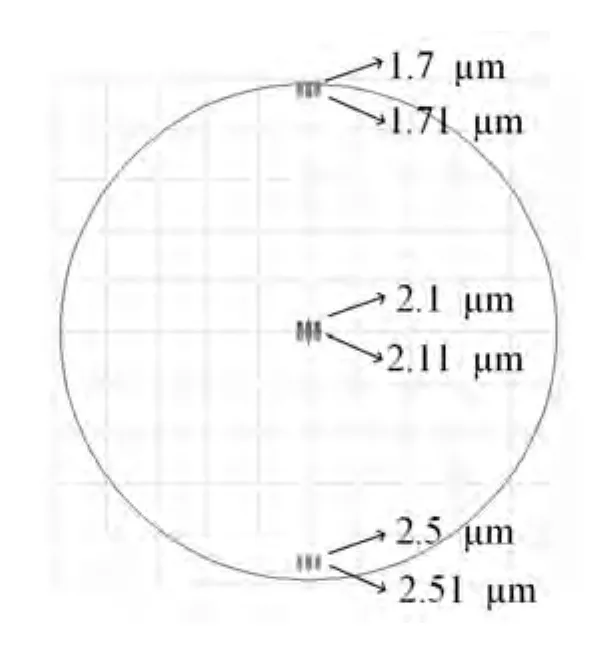
图16 1700~2500 nm像面光迹图Fig.16 Image surface trace diagram in the band of 1700-2500 nm
将前置光路和色散光路组合,图17即为完整的900~2500 nm波段Czerny-Turner光谱仪光路图。
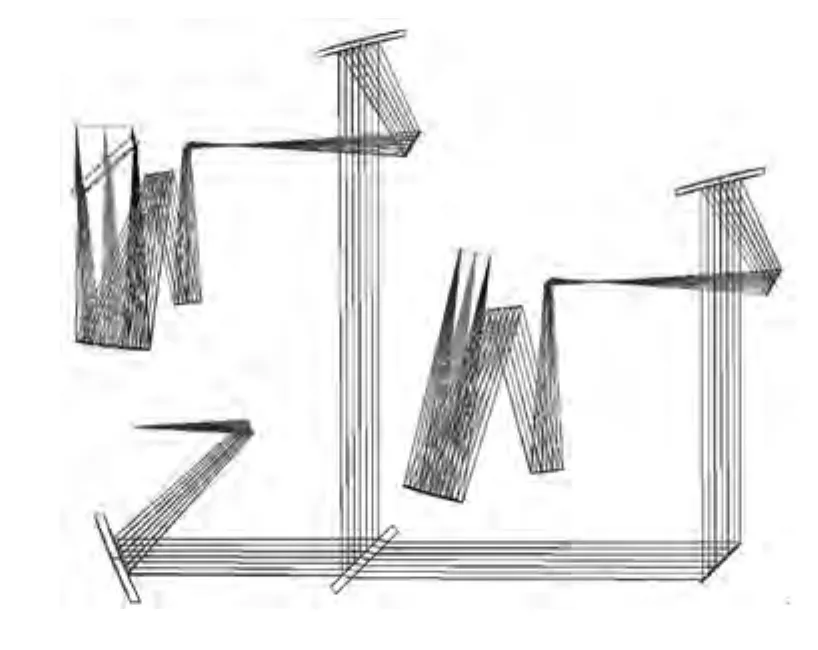
图17 全波段Czerny-Turner光谱仪光路Fig.17 Optical path of the full-band Czerny-Turner spectrometer
5 结论
为了满足宽波段高光谱Czerny-Turner结构光谱仪的要求,基于像差理论,通过光栅产生的像散补偿球面反射镜的像散,以及通过柱面镜引入相反像散补偿剩余像散,以达到全波段消像散的要求,从而提高Czerny-Turner结构光谱仪成像系统的分辨率。推导出光栅和柱面镜补偿像散的基础公式,分别设计出波段为900~1700 nm和1700~2500 nm全波段消像散的Czerny-Turner光谱仪成像系统,并通过前置光路将两部分组合。通过ZEMAX的优化分析可得,Czerny-Turner光谱仪在全波段范围内不仅达到消像散要求,还得到较好的成像质量。
