小波阈值去噪在偏滤器光谱信号处理中的应用

章志涛,丁芳,罗宇,陈夏华,叶大为,胡振华,罗广南

(1中国科学院合肥物质科学研究院等离子体物理研究所,安徽 合肥 230031;2中国科学技术大学,安徽 合肥 230026)

0 引言

全超导托卡马克东方超环(EAST)[1]装置是我国探索核聚变能源的前沿装置,但由于其在实验运行过程中会产生巨大的能量,目前普遍使用采集实验运行时装置内部粒子发射光谱的方式进行间接物理分析。钨(W)原子由于其高熔点、高热导率、低溅射率、低燃料滞留等优良特性被广泛用于托卡马克装置偏滤器面向等离子体材料,也是下一代聚变堆首选的第一壁材料[2]。在强大的热流粒子流轰击下,钨的溅射刻蚀不仅会影响部件寿命,产生的钨原子进入芯部等离子体后也会造成严重的辐射损失。对钨原子光谱信号进行监测分析是研究钨溅射刻蚀过程的一个重要手段。但是由于偏滤器钨原子光谱信号采集过程中,易受到光源噪声、实验环境、仪器本身和暗电流噪声等诸多因素的干扰和影响,光谱信号上会产生大量波动、毛刺。因此,如何高效且准确地消除噪声干扰、提高光谱信号信噪比的同时保留原有信号特征是后续利用钨原子光谱信号准确分析相关物理过程的关键因素。

迄今为止,适用于光谱信号去噪的方法有很多,如傅里叶变换法[3]、平滑法[4]、中值滤波法[5]、卡尔曼滤波法[6]等。但这些方法存在着诸如难以解析信号的局部信息、容易滤除信号的细节部分等问题。而小波变换具有可平移、可伸缩、多尺度、多分辨率等多方面的优势,其在时域和频域均具有良好的局部化性质,能同时较好地处理时域和频域分辨率之间的冲突问题,从而有效地从光谱信号中提取有用信息[7]。目前较常使用的小波去噪方法主要为以下三种:模极大值重构去噪法、相关性去噪法、小波阈值去噪法[8]。

然而,模极大值去噪法[9]、相关性去噪法[10]都有着计算过程较复杂、计算量较大、不能适应大批量数据同时处理的情况,因而工程应用较少。小波阈值去噪则是将光谱信号分解成不同的小波系数,通过合适的阈值去除含有噪声的小波系数,最后重构出信号。该法计算过程简便,运算量较少,并且去噪效果明显[11]。

本文结合信噪比(SNR)和均方根误差(RMSE)量化去噪效果,通过对比分析不同小波基函数和4种阈值计算规则匹配去噪的仿真实验,得出最佳小波基和阈值计算规则的组合参数;进而利用该组合参数对实际EAST偏滤器钨原子光谱信号进行消噪处理,得到消噪后钨原子光谱信号,为后续使用该数据进行分析计算带来便利,进而有利于加深对EAST实验中相关物理过程的理解。

1 小波阈值去噪原理、步骤和评价指标

1.1 小波阈值去噪原理

一般光谱信号f(t)表达式为

式中:s(t)为纯净信号;n(t)为标准高斯白噪声,其方差服从N(0,σ2)。

对于一维连续信号f(t)来说,其小波变换为

式中:w、θ、z分别为原始信号、纯净信号、噪声的小波系数。

小波阈值去噪方法的原理是:设置一适当阈值W,认为小于该阈值的小波系数对应噪声部分,将其置零;适当保留大于阈值的系数,从而达到去噪的目的。

1.2 小波阈值去噪步骤

小波阈值去噪算法主要通过以下三个步骤实现[12]:1)对含噪信号f进行某个尺度的小波变换,得到其对应小波系数序列w;2)设定临界阈值W作为门限对小波系数序列w进行处理,得到纯净信号小波系数θ的估值;3)对处理后小波系数的估值θ进行小波逆变换,得到重构信号 ˆf。图1为小波阈值去噪流程图。

图1 小波阈值去噪流程图Fig.1 Flow chart of wavelet threshold denoising process

1.3 去噪效果评价指标

为了定量评价去噪效果,引入了评价指标:信噪比(SNR)和均方根误差(RMSE),其为衡量信号去噪效果的重要依据[13]。

SNR和RMSE的计算公式可分别表示为

评估标准:SNR值RSN越大,RMSE值ERMS越小,去噪效果越好。

2 小波基函数、分解层数和阈值规则

信号类型不同,混合的噪声性质和强度也不同,因此小波阈值去噪的参数选择因信号而异。合适的参数选择才能最大程度地去除声原始信号中的噪声,同时又可以有效保留有用信号,避免信号失真。

2.1 小波基函数

不同小波基函数特性不一,选择具有较好正交对称紧支撑特性的小波基函数,可在减少计算量的同时避免信号在分解和重构过程中产生失真。sym小波系和db小波系均属于正交的时域紧支小波,但sym小波系较db小波系对称性更好,这一特性可使其在信号分解与重构过程中避免信号失真[14]。由此,从sym小波系中选取小波基函数,表达式为symN(N=2,3,···,9)。

2.2 阈值规则[15]

在小波阈值去噪中阈值规则的选定分为两个部分,即阈值计算规则和阈值函数的选取。合适的阈值规则能够使信号去噪效果更佳。

2.2.1 阈值计算规则

阈值计算规则包括四类:无偏估计阈值(rigrsure)、固定式阈值(sqtwolog)、启发式阈值(heursure)和极大极小阈值(minimaxi)。

1)无偏估计阈值。即一种基于Stein的无偏似然估计原理的自适应阈值计算规则,计算出每个阈值对应的风险值,风险最小的即为所选。

2)固定式阈值。通过公式计算出一个固定阈值进行处理,计算公式可表示为

式中:σn为噪声标准方差,N表示信号长度。

3)启发式阈值。源自无偏估计阈值的启发式算法的变形,本质上是无偏阈值和固定阈值的综合。若信噪比较小就采用无偏估计阈值,相反,则选择固定式阈值。

4)极大极小阈值。采用极大极小的原则来选择阈值,获得的是一个最小均方误差的极值。

此处通过仿真信号在同一小波基函数下的去噪效果进行定量的对比分析来进一步确认使用哪种阈值计算规则效果最佳。

2.2.2 阈值函数的选取

目前常用的阈值处理函数有:硬阈值函数和软阈值函数。硬阈值函数计算简便,但是在某些点会产生间断;软阈值函数可以有效避免间断,使重建信号更为光滑,连续性更佳,但由于处理后的小波系数与实际小波系数存在恒定偏差,重构时信号易产生形变失真。

为了克服传统阈值函数的缺点,调研了基于上述缺陷进行的改进,诸如半软阈值法、折中阈值法等。在此引入Wu等[16]改进的渐进半软阈值函数,其定义为

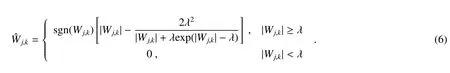
图2为三种阈值函数的对比,由图可见该渐进半软阈值函数在阈值处是连续的,不会引起重构时的振荡,优化了硬阈值函数存在间断点的不足。当小波系数的绝对值大于阈值时,小波系数收缩,且当|Wj,k|不断增大时,重构的小波系数与真实小波系数间的偏差逐渐减小,弥补了软阈值函数的缺陷。

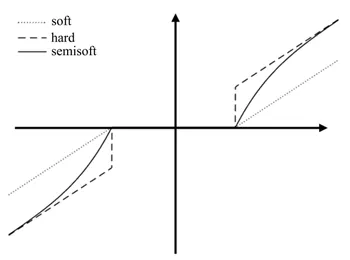
图2 三种阈值函数对比Fig.2 Comparison of three threshold functions

3 仿真实验

仿真实验中,参照偏滤器钨原子光谱信号在边缘局域模(ELM)[17]期间的理论谱型,生成与其近似的仿真含噪信号,进而使用不同的sym小波基函数和阈值计算规则匹配去噪,进行4层小波分解,获得去噪后的信号。通过计算消噪后仿真信号的SNR和RMSE来定量比较去噪效果的优劣,从而得到去噪效果较好的匹配参数。

3.1 原始仿真信号

根据偏滤器钨原子光谱信号在ELM期间的理论谱型绘制原始仿真信号s(λ)[图3(a)],其可表示为

式中H、λ0分别为仿真信号峰高、峰位置参数。考虑到真实信号主要噪声来源为仪器内部的热噪声、散粒噪声等,是典型的高斯白噪声。利用MATLAB 2018b平台中awgn()函数加入SNR为18的高斯白噪声,得到含噪信号f(λ),如图3(b)所示。

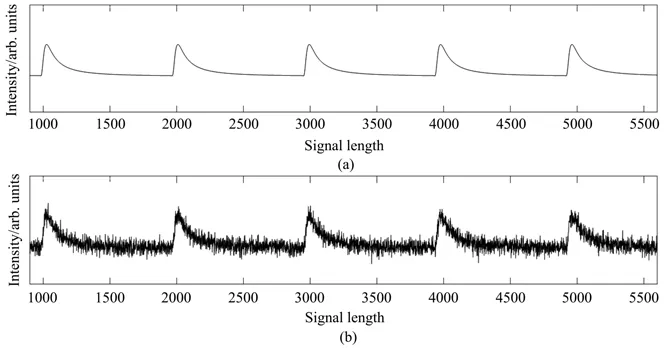
图3 (a)原始仿真信号s(λ);(b)含噪仿真信号 f(λ)Fig.3 (a)Raw simulation signal s(λ);(b)Noise simulation signal f(λ)

3.2 仿真实验结果与分析

选取sym2小波基函数时,对仿真的含噪信号分别用4种阈值规则进行消噪得到的对比效果如图4所示。

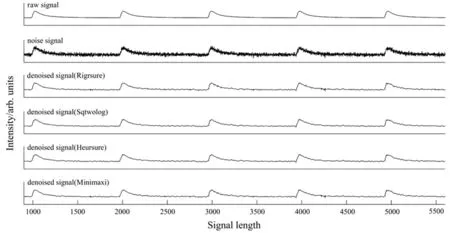
图4 基于sym2小波基函数的去噪效果Fig.4 Denoising effect based on sym2 basis function

表1为选用sym2小波基函数时去噪后的SNR和RMSE数值对比。根据去噪效果评估标准,按去噪效果优劣进行排列,1为最佳。由此可见,同一小波基函数下启发式阈值计算规则去噪效果最佳。

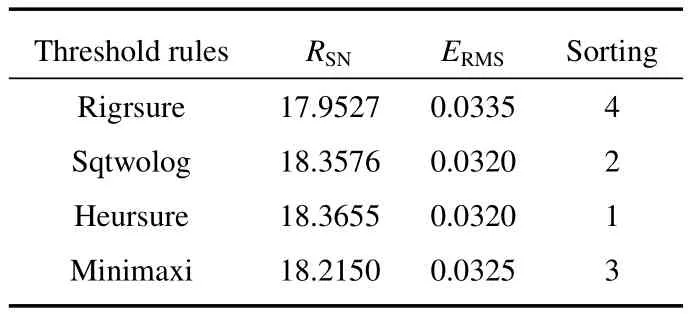
表1 sym2小波基函数匹配4种阈值计算规则的去噪效果Table 1 Denoising effect of sym2 basis wavelet matching 4 kinds of threshold rules

在启发式阈值计算规则参数下,进一步对比不同sym小波基函数下信号的去噪效果,SNR和RMSE计算结果如图5所示。

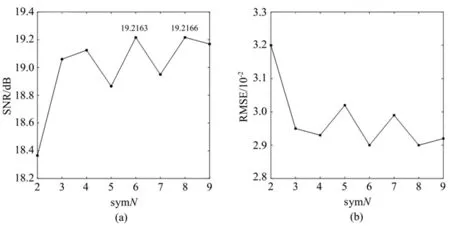
图5 不同symN小波基函数的信噪比(a)和均方根误差(b)Fig.5 The SNR(a)and RMSE(b)with different symN

结合上述仿真实验及图5中SNR、RMSE定量对比可得出:针对该仿真实验中的含噪信号,选用sym8小波基函数,匹配使用渐进半软阈值函数、启发式阈值计算规则,且小波分解层数为4时,信噪比取得最大值19.2166,均方根误差取得最小值0.0290,此时去噪效果相对较好。

4 应用实验

4.1 偏滤器光谱信号

实际信号来源是基于EAST钨偏滤器重杂质光谱诊断平台采集到的偏滤器钨原子光谱信号,使用的采集设备是光电倍增管(PMT-H7827),采样频率为250 kHz。对63883次实验中钨(W)原子光谱信号进行小波消噪处理,W信号在ELM期间信号如图6所示。可见,该段信号包含6个信号峰,谱峰峰型基本一致,上升沿陡峭、下降沿较平缓;信号中含有大量毛刺且频率较高,不利于通过获取谱峰特征来进一步分析EML期间的物理过程。

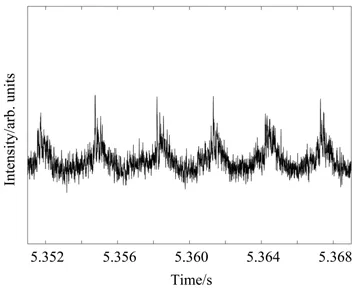
图6 5.351～5.369 s,ELM期间W原子光谱信号Fig.6 5.351～5.369 s,W signal during ELM

4.2 小波去噪处理结果及分析

参照仿真实验得到的最佳参数匹配,对W信号进行渐进半软阈值小波去噪处理。去噪后信号如图7所示。对比图7(a)、(b)可知,W信号中幅度较大、频率较高的干扰信号被较好地滤除,仅剩幅值较小的干扰信号。可见,仿真实验取得的最佳参数匹配结合渐进半软阈值函数对实际信号的去噪效果明显,能够在保留信号中有用信息的情况下消除较多噪声。

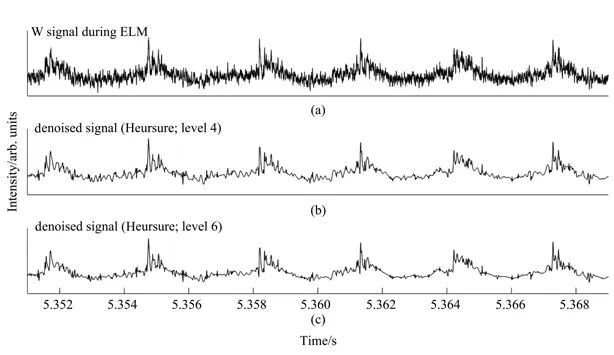
图7 ELM期间W信号的去噪效果对比图。(a)含噪信号;(b)4层分解;(c)6层分解Fig.7 Comparison of denoising effect of W signal during ELM.(a)Noisy signal;(b)4-layer decomposition;(c)6-layer decomposition

进一步实验发现,适当增加小波分解层数,当分解层数设置为6时,去噪后信号如图7(c)所示。对比图7(b)可见信号更加光滑,信号中毛刺进一步减少。

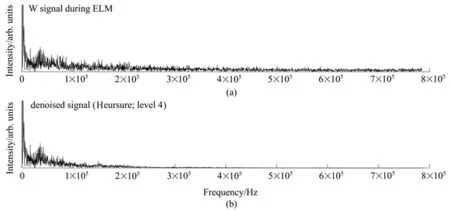
图8 去噪前后频谱图。(a)含噪信号;(b)去噪后信号Fig.8 Frequency spectrum before and after denoising.(a)Noisy signal;(b)Denoised signal

频谱图可以从频域对实测信号进行分析,实测信号中包含的干扰信号通常表现为高频成分,而有用信号则表现为低频成分。从图8的频谱图中可以看出,去噪后信号保留了50 kHz以下的低频有用信号,剔除了250 kHz以上的高频干扰信号,同时对50～250 kHz的混合信号进行了适当保留。即小波阈值去噪方法基本将高频噪声成功剔除,而低频有用信息则被保留。

5 结论

受采集仪器等诸多因素影响,实测偏滤器原子光谱信号不可避免地存在噪声,利用其进行物理过程分析及计算前需对其进行处理。研究了结合改进的渐进半软阈值函数的小波阈值去噪方法在偏滤器W原子光谱信号上的去噪效果。根据实际信号理论模型构建仿真实验,并将仿真实验得到的最优参数配置应用于实测信号去噪处理,结合主观视觉效果和客观频谱分析判断其取得了较好的去噪效果。进一步实验发现,小波分解层数的变化可在一定程度优化去噪效果。

通过成功处理实测偏滤器W原子光谱信号,为后续进一步利用W原子光谱分析理解实验中相关物理过程奠定了基础。同时在研究过程中发现,该方法针对其他粒子发射光谱的去噪处理均有明显效果,可有效去除实测光谱信号中的高频噪声,具有较好的应用价值。