顾及卫星间相关性的Kalman短期钟差预报
2022-06-10王潜心吕伟才钟东升谭福临
杨 旭,王潜心,吕伟才,钟东升,谭福临
(1.安徽理工大学矿区环境与灾害协同监测煤炭行业工程研究中心,安徽 淮南 232001;
2.安徽理工大学 空间信息与测绘工程学院,安徽 淮南 232001;
3.安徽理工大学矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室,安徽 淮南 232001;4.中国矿业大学 环境与测绘学院,江苏 徐州 221116)
0 引言
全球卫星导航系统(global navigation satellite system, GNSS)卫星钟差短期预报(一天以内)是GNSS应用中的一个重要问题,对实时精密单点定位技术(precise point positioning,PPP)、GNSS系统间时间同步等方面研究具有重要作用[1]。现有卫星钟差短期预报研究已对预报模型本身研究较多,对建模策略、方式正在进一步拓展。文献[2]利用卡尔曼(Kalman)滤波、递推最小二乘和灰色模型GM(1,1)进行了一天内的卫星钟差短期预报,结果表明 Kalman滤波预报精度最高。文献[3]在对比线性模型、二次多项式模型、灰色模型以及Kalman滤波模型预报精度后,也得出Kalman滤波模型的短期预报精度最高。文献[4]利用哈达玛(Hadamard)总方差,计算了Kalman滤波预报模型观测与状态噪声协方差阵,得到的全球定位系统(global positioning system, GPS)Block IIR铷原子钟(Rb)的短期预报结果,验证了该模型的正确性。文献[5]提出将预报残差周期项应用到北斗卫星导航系统(BeiDou navigation satellite system,BDS)卫星超短期钟差预报模型中,利用德国地学研究中心(Deutsches GeoForschungsZentrum, GFZ)的事后多GNSS精密钟差(GFZ multi-GNSS precise clock, GBM)进行仿真,其结果表明,三类BDS卫星在1 h的预报时间内,其精度整体优于0.8 ns,2和 3 h的预报精度较传统线性模型提高了4%~20%。文献[6]利用星地双向时间比对(twoway time transfer, TWTT)与轨道确定与时间同步(orbit determination and time synchronization,ODTS)获得的钟差数据,对BDS卫星钟的随机特征、周期特征进行了分析,设计了顾及该特征的Kalman滤波算法,实现了TWTT和ODTS钟差数据的融合,验证了该算法应用到卫星钟差短期预报的正确性。文献[7]提出一种多项式同时结合周期项与反向传播(back propagation, BP)神经网络的BDS钟差预报模型,对国际GNSS监测评估系统(international GNSS monitoring and assessment system,iGMAS)与 GFZ的超快速钟差数据进行了预报,3、6、12及24 h的预报精度较原产品提高了10.34% ~26.14%。文献[8-9]研究了法国空间研究中心(Centre National D'Etudes Spatiales,CNES)的状态域空间表达(state space representation,SSR)改正数更新频率及中断时间间隔对多系统实时 PPP的影响,结果表明在 PPP服务端,SSR更新频率低于60 s;在PPP用户端,SSR改正数中断超过360 s时,均会明显降低PPP收敛时间和定位精度。
由以上研究结果可以看出,对于卫星钟差短期预报,在单一预报模型中,Kalman滤波模型较其他模型具有一定优势;组合模型或单一模型的改进一般从顾及卫星钟物理、周期、随机特征等方面考虑;卫星钟差实时预报对实时 PPP较为关键。但这些模型仍存在一定的局限性:部分单一模型不适合实时预报;组合模型存在模型复杂度高且执行效率低等问题;仅针对单一卫星钟差序列进行建模预报时,没有考虑各卫星之间的相关性。针对上述不足,本文进一步拓展Kalman滤波算法在卫星钟差中的建模方式与策略,以此来提高钟差预报性能;拟对GBM产品采用一种顾及卫星间相关性的Kalman滤波预报算法,并结合阿伦(Allan)方差和Hadamard方差来进行四大卫星导航系统的卫星钟差超短期(3 h以内)或短期预报,并与传统的Kalman滤波短期预报方法进行对比分析。
1 卫星钟差预报的Kalman算法模型
原子钟随机模型与幂律谱噪声模型符合较好,由5种独立的噪声构成[10],该噪声的表现与取样时间有关:在卫星钟中短期取样时间内(15 d以内),卫星钟一般只具有1~3种噪声[11]。本文基于三状态(调相随机游走,调频随机游走,调频随机奔跑噪声)Kalman滤波模型研究卫星钟差短期预报。
1.1 钟差模型
对第k历元、第j颗卫星建立的原子钟钟差Kalman滤波模型为
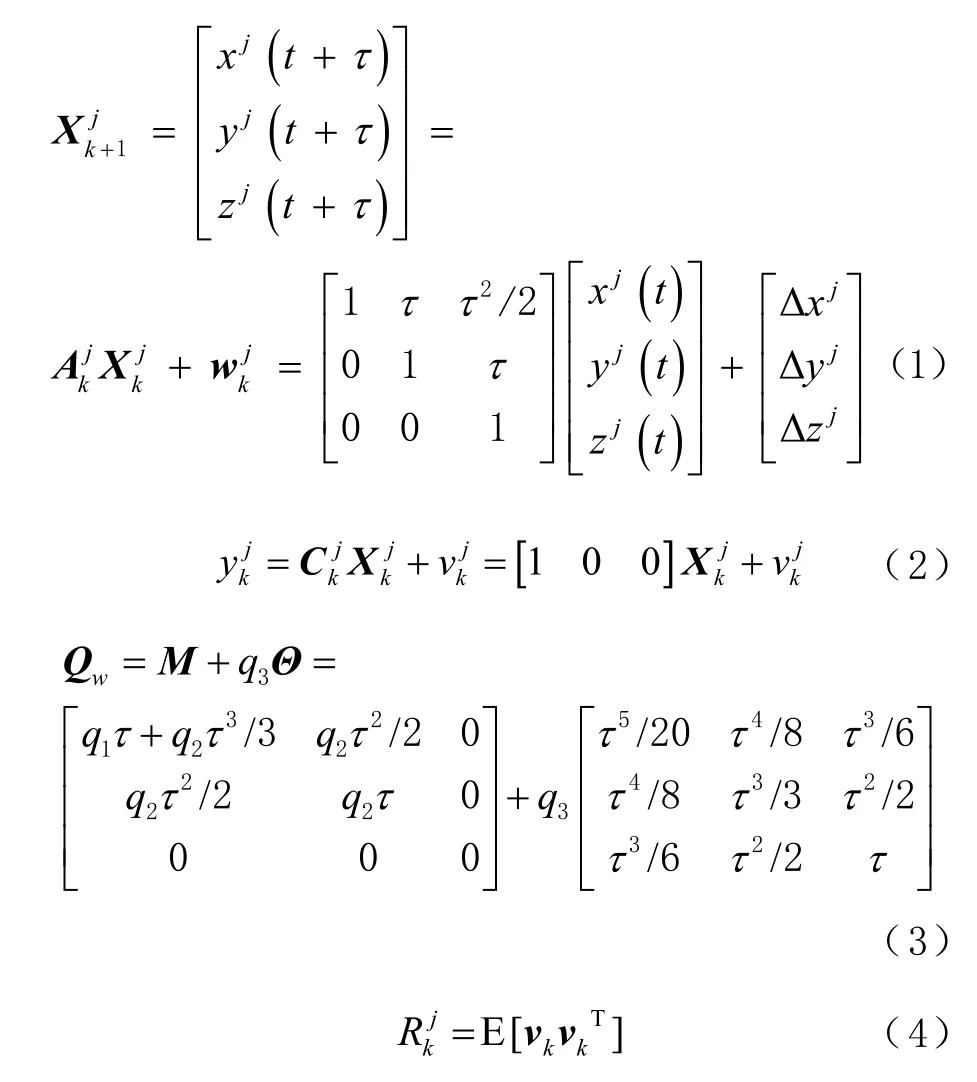
式中:τ为预报时间;x(t)为t时刻的钟差;y(t)为x(t)的时间导数;z(t)为y(t)的时间导数;Δx、Δy、Δz分别为独立于x(t)、y(t)、z(t)的随机模型误差,其过程噪声分别为q1、q2、q3;wk为模型状态噪声,其协方差矩阵为Qw;vk为模型的观测噪声,其噪声方差为Rk。
1.2 噪声方差阵推导
通过Allan方差或Hadamard方差可求取式(3)中与卫星钟频率稳定度相关的Qw。
1)Allan/Hadamard方差计算。铯原子(Cs)钟的频率稳定性常用Allan方差来描述[12-13],对于相位偏差数据{xn,n= 1 ,2,… ,N},N为采样个数,Allan方差为
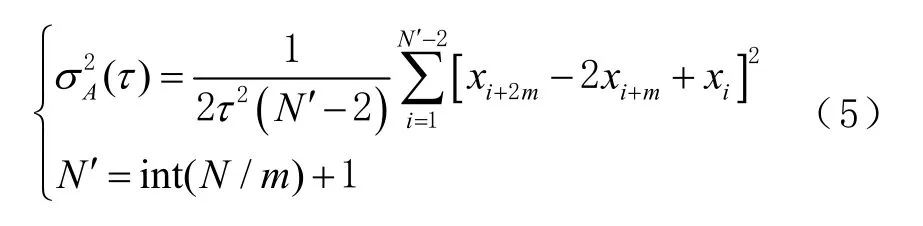
式中:τ=mτ0为平滑时间;τ0为相邻钟差相位数据采样间隔;m为平滑因子,一般取1 ≤m≤ in t[(N′−1)/3];N′为按照τ大小间隔的相位数据个数。
Rb钟频漂项较为明显,常用 Hadamard方差描述其频率稳定性,利用相位偏差数据计算的Hadamard 方差[14]为

同时考虑式(3)中的3种钟差调频噪声与调相白噪声时,式(5)与式(6)中的方差分别为

式中,q0为调相白噪声的测量噪声参数。
2)噪声矩阵求解。式(5)、式(6)中,τ取不同值,可得不同的Allan、Hadamard方差值,再联立式(7)、式(8),q1、q2、q3和q0可利用最小二乘算法进行估计,进而可确定式(3)、式(4)中的Qw、Rk。
1.3 顾及卫星间相关性的Kalman滤波卫星钟差短期预报模型
目前,基于Kalman滤波的钟差建模与预报多数情况下都是基于一颗卫星进行的,鲜有针对多颗卫星进行整体建模与预报。同时,卫星轨道等误差会影响多卫星导航融合估计的卫星钟差,卫星的空间环境也会干扰星载原子钟的运行,这些因素均会使估计的卫星钟差存在一定的相关性。本节将推导顾及这种相关性影响的情况下,Kalman滤波钟差预报模型。
假设第k历元共有n颗卫星,顾及卫星间相关性的Kalman滤波钟差预报模型可表达为

式中:sk,ηk分别为模型状态噪声与观测噪声,对应的协方差阵和噪声方差阵分别为w′Q、Rk,由式(1)至式(4)可知

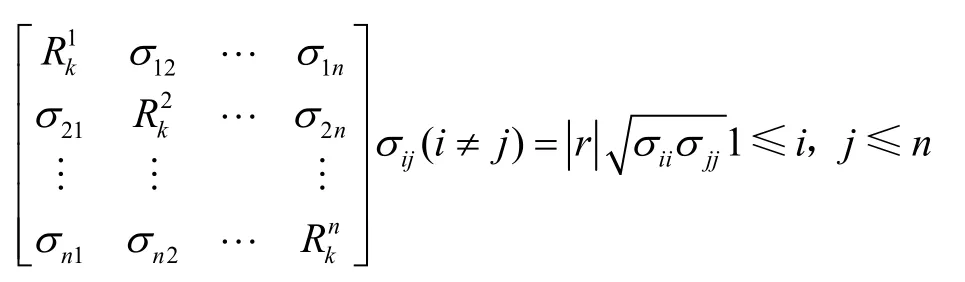
式中:ijσ、r分别为第i颗卫星和第j颗卫星之间的协方差及相关系数。
r可由皮尔逊相关系数(pearson correlation coefficient)公式计算[15],其计算方法为

式中:d为钟差预报采用的基础数据个数;gi、ui分别为该基础数据利用二次多项式拟合后的两卫星拟合残差的时间序列;分别为gi、ui的均值;r为两时间序列间相关关系密切程度的强弱,r为0时表示无线性相关关系,r越大,相关程度越高。
以上过程为顾及卫星间相关性的Kalman滤波模型,考虑相关性的二次多项式、二次多项式加周期项的预报模型均与以上步骤类似,此处未列出。
2 多系统钟差数据特征分析
本文利用事后钟差,设计顾及卫星钟差随机特征与周期特征的预报方法进行预报实验,以此来检验文中所提新方法的可靠性和有效性。本文选取了2019年年积日第14—40天共27天GBM钟差产品(30 s采样间隔)、共84颗卫星参与了数据特征分析,这些导航卫星分别为C01、C02、C03、C04、C05、C06、C07、C08、C09、C10、C11、C12、C13、C14等 14颗 BDS卫星;G01、G02、G03、G04、G05、G06、G07、G08、G09、G10、G11、G12、G13、G14、G15、G16、G17、G18、G19、G20、G21、G22、G23、G24、G25、G26、G27、G28、G29、G30、G31、G32等 32颗 GPS卫星;R01、R02、R03、R04、R05、R07、R08、R09、R10、R11、R13、R14、R15、R16、R17、R18、R19、R20、R21、R22、R23、R24等22颗俄罗斯格洛纳斯卫星导航系统(global navigation satellite system,GLONASS)卫星;E01、E02、E03、E04、E05、E07、E08、E09、E11、E12、E14、E18、E19、E24、E26、E30等 16颗欧盟伽利略卫星导航系统(Galileo navigation satellite system, Galileo)卫星。该 84颗卫星轨道类型及卫星钟类型参见文献[16]。以C13、G01、R01及E01为参考卫星,利用二次差法计算的标准偏差(standard deviation, STD)进行钟差精度统计[17]。利用文献[5]卫星钟单天解基准处理方法,消除GBM天与天产品之间存在的系统性钟差基准偏差,同时利用文献[18]改进的巴尔达(Baarda)粗差探测法,对该钟差序列进行数据预处理。
2.1 频率稳定性分析
利用 Allan方差、Hadamard方差计算的连续27天四系统按照卫星轨道类型分类的卫星钟千秒稳,万秒稳,天稳定性结果及卫星钟的噪声水平q0,q1,q2,q3统计结果见图1。

由图1可知:
1)Allan方差和Hadamard方差计算的频率稳定性指标基本一致,GLONASS卫星的频率稳定性较差,GPS II-F卫星钟、Galileo完全运行能力(full operational capability, FOC)卫星钟、Galileo在轨验证(design and on-orbit verification, IOV)卫星钟的频率稳定性较高。
2)Allan方差和Hadamard方差计算的噪声水平基本一致,各卫星系统的原子钟噪声水平变化规律和其频率稳定性变化规律一致。
2.2 周期特性分析
由于卫星轨道和卫星钟差高度相关,使得钟差数据有一定的周期性。去除上述27天钟差数据的二次趋势项之后,得到相应的钟差残差数据,利用快速傅里叶变换(fast Fourier transform, FFT)方法获取钟差的主要频率来分析其周期特性。图2是GBM产品数据完整率较高的C03,C07,C13,G01,R15,E01卫星钟差主频率分析结果,横轴为一天中出现某个周期的次数。表1是连续 27天 GBM钟差产品两个主周期的统计结果。

图2 GBM产品C03,C07,C13,G01,R15,E01卫星振幅频谱

表1 GBM产品主周期、第二周期统计结果 单位:h

(续)
由图2及表1可知:
GBM钟差有一定的周期性,且随着周期的缩短,振幅有逐渐降低的趋势。对于BDS,GBM产品中有较明显的12、24 h周期;对于GPS,GBM产品中有较明显的6、12 h周期;对于GLONASS,GBM产品中有较明显的11 h周期;对于Galileo,GBM产品中有较明显的7、14 h周期。
2)GBM钟差的周期性与卫星系统有关;对于每个卫星系统,卫星的周期性与卫星轨道类型的相关性不强。卫星钟差周期不一致的原因有:①轨道周期的耦合影响;②昼夜环境变化;③拟合残差存在误差;④钟差数据部分缺失。
3)分析出周期项后,就可以利用考虑周期影响的Kalman滤波,附加周期项的二次多项式等模型进行钟差预报。
3 多系统钟差短期预报分析
为了验证本文所提顾及卫星间相关性方法的有效性,与传统Kalman滤波、二次多项式、附周期项的二次多项式预报模型进行预报性能比较,设计了4种预报实验:1)方案1,Kalman滤波模型预报;2)方案2,顾及相关性的Kalman滤波模型预报;3)方案3,附加周期项二次多项式预报;4)方案 4,顾及相关性的附加周期项二次多项式预报。Cs钟,Rb钟、氢原子(Ph)钟分别采用Allan方差、Hadamard方差计算 Kalman滤波模型中的状态噪声。
利用前一天钟差数据(30 s间隔)求取Kalman滤波模型状态噪声、卫星间的相关性、二次多项式拟合系数与2个主要周期之后,预报后一天1、3、6、12及24 h的数据(30 s间隔);钟差精度统计时,采用与自身GBM产品比较。
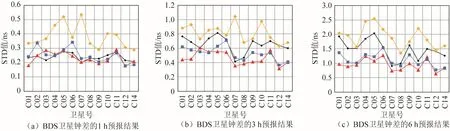
图3为4种方案下连续26天(2019年年积日第15—40天)四系统卫星钟差5种预报时长下的预报精度,表2为不同预报方案精度统计与对比分析结果。

表2 GBM产品不同方案四系统卫星钟差预报精度及方案间精度对比统计结果

图3 GBM产品方案1(圆点)、2(三角形)、3(菱形)、4(正方形)四系统卫星钟差1、3、6、12及24 h预报精度


(续)
由图3与表2统计结果可知:
卫星系统不同,预报精度不同:对于6 h以内的预报,精度最低的是 GLONASS,最高的是Galileo,GPS、BDS次之;对于超过12 h的预报,BDS、GLONASS的预报精度相对较差,次于Galileo、GPS;在BDS,GPS中,不同卫星轨道、卫星钟类型的卫星钟差预报精度不尽相同,BDS中的部分倾斜地球同步轨道(inclined geosynchronous orbits, IGSO)卫星预报精度优于地球静止轨道(geostationary Earth orbit, GEO)卫星;多数GPS II-R卫星预报精度比GPS II-F卫星差,多数配备Rb钟的卫星比Cs钟的卫星(G08,G24)精度要高;在GLONASS、Galileo中,卫星轨道、
卫星钟类型对卫星预报精度影响较小,除R10、R13、R19、E08及E18卫星外,系统内其他卫星预报精度基本相同。
预报方案不同,预报精度不同:①整体上,方案3预报精度最差,方案2、方案4的预报精度最好,方案1次之;②方案2相对于方案1,在BDS、Galileo中提升率较高,BDS的提升率最大可达36.79%,GLONASS的提升率较低;同时表现出随着预报时长增加,预报精度提升率逐渐增加的特征;③方案4相对于方案3,四系统均有较高的提升率,平均提升率为35.19%;④方案2相对于方案4,BDS有较高的提升率,在1、3 h预报中,四系统中均有较好的提升率;对于GPS,GLONASS,Galileo,随着预报时长的增加,方案4具有比方案2更优的预报性能;⑤方案3在预报时长为1、3、6及12 h时,多数卫星的预报精度劣于其他方案,这也说明在12 h内的卫星钟差预报中,Kalman滤波模型和考虑相关性的预报模型更具有预报优势。
由上可知,顾及卫星间相关性的Kalman滤波、附加周期项二次多项式模型均比相应不考虑相关性的模型预报精度好,主要原因在于多卫星系统钟差整体估计是基于多卫星系统联合定轨同时解算轨道和钟差得到的。对多颗卫星进行整体建模与预报,不仅能够很好地顾及卫星钟差序列之间的一致性,还能够通过高稳定度的卫星提高低稳定度卫星钟差序列的建模精度,从而提高多颗卫星整体预报精度。同时从表1、表2可知,对于四系统钟差产品,存在6、7、11、12及24 h等周期,在这些周期以内的预报(时长为1、3 h),顾及卫星间相关性的Kalman滤波模型较顾及卫星间相关性的附加周期项二次多项式模型、附加周期项二次多项式、Kalman滤波模型更具优势,分别提升了8.95 %,46.66 %,7.35 %,最大可提升12.77 %(GLONASS)、57.16 %(Galileo)、28.35 %(BDS),而在大于这些周期以外的预报,顾及卫星间相关性的Kalman滤波模型的预报精度绝大多数情况是次优的,可能是由于该模型没有顾及卫星钟差的周期特征引起的。
4 结束语
本文推导了顾及卫星间相关性的Kalman钟差预报模型,分析了连续27天GBM最终产品的频率稳定性、周期特性,设计了4种实验方案来比较分析所提方法在钟差短期预报中的正确性和有效性,主要实验结果如下:
1)卫星钟类型、卫星轨道类型对卫星钟差频率稳定性有一定影响,配备Cs钟的GLONASS卫星频率稳定性较差,配备 Ph钟的 Galileo卫星频率稳定性较高;GPS II-F,Galileo IOV、Galileo FOC的卫星钟频率稳定性较高;同时对卫星预报精度也有影响;
2)GBM的 BDS,GPS,GLONASS及 Galileo卫星钟差都有一定的周期性,分别有较明显的12、24,6、12,11,7、14 h 周期。
3)在GBM钟差数据的预报中:①顾及卫星间相关性的Kalman滤波预报模型较传统Kalman滤波模型精度平均提升了 15.11%,提升率最大值为36.56%(Galileo),BDS提升效果最好;②顾及卫星间相关性的附加周期二次多项式预报模型较附加周期二次多项式预报模型精度平均提升了28.93%,最大提升率为51.95%(GPS),四系统提升效果相当;③在1、3 h的预报中,顾及卫星间相关性的Kalman滤波较顾及卫星间相关性附加周期的二次多项式预报模型精度平均提升了 8.95%,提升率最大值为12.77%(GLONASS)。
