多星座组合RAIM技术在列车定位中的应用

铁凯博，米根锁，王彦快

（兰州交通大学, 自动化与电气工程学院, 兰州 730070）

0 引言

列车定位精度直接影响列车的运行安全，提高列车定位的精度和可靠性已经成为不可忽视的重要目标[1]。全球卫星导航系统（global navigation satellite system, GNSS）在铁路领域已广泛应用，但在列车实际运行过程中，卫星出现故障，会导致定位结果不准确[2]，这就要求导航系统能对所用卫星进行实时检测，剔除出现故障的卫星。因此，有学者提出将接收机自主完好性监测（receiver autonomous integrity monitoring，RAIM）技术[3]应用于列车定位。文献[4]提出了RAIM技术在列车定位中的可用性预测方法，并对该技术在铁路领域内的可用性做出了判断；文献[5]将RAIM技术应用于北斗卫星导航系统（BeiDou navigation satellite system，BDS）的列车定位中，提出沿股道水平保护级（along track protect level，ATPL）算法，提高了RAIM技术在列车定位中的可用性；文献[6]分析了BDS完好性问题在列车定位中的风险，并设计了BDS RAIM可用性预测系统，保障了RAIM预测结果的可靠性；文献[7]在故障卫星检测环节中引入加权因子，降低检测过程中的漏警率，提高了列车定位精度。文献[8]解决了GNSS性能指标与铁路可用性指标的映射问题，为基于GNSS的 RAIM 算法在铁路领域中的应用提供了参考。通过分析文献可知：目前主要针对单星座RAIM 在列车定位中的应用进行了研究，单星座RAIM应于列车定位时，常会出现因可见星不足或几何分布较差而降低算法可用性的情况，进而影响算法的故障检测率和故障识别率。由于可见星数目的限制，单星座 RAIM 在某些高海拔铁路定位精度并不高[9]，甚至不能使用，RAIM算法在铁路领域内的研究还处于起步阶段。

鉴于此，本文提出了将多星座RAIM技术应用于列车定位，通过增加可见星数目提高RAIM算法的可用性。在构造多星座系统观测方程的基础上，采用奇偶矢量法对导航卫星进行故障检测。通过青藏铁路列车定位数据对全球定位系统（global positioning system, GPS）、伽利略卫星导航系统（Galileo satellite navigation system, Galileo）和 BDS多星座组合RAIM和GPS单星座RAIM进行对比仿真，分析多星座RAIM在列车定位中的检测性能。

1 多星座系统列车定位原理

1.1 时空基准统一

为构成基于列车定位的多星座导航系统，需将不同星座的时间系统进行统一，坐标系统进行转换，采用相同的时间和坐标标准，实现多星座系统的数据融合[10-11]。本文将多星座时间、坐标系统统一转换为以GPS为基准。转换过程如下：

1）将Galileo系统时（Galileo system time, GST）转化为GPS时（GPS time, GPST）的计算公式为

式中：TGPST为 GPS时；TGST为 Galileo系统时；TGGTO为GPST与GST间的偏差；A0G、A1G、t0G和SWNOG分别为时间偏差的常数项、变化率、参考时间和参考星期个数；TTOW为星期内的时间；T是常数，为604 800；SWN为Galileo的星期个数；mod为求余函数。

2）将北斗时（BDS time, BDT）转化为GPST的计算公式为

式中，TBDT为北斗系统时。

3）将格洛纳斯卫星导航系统（global navigation satellite system, GLONASS）时（GLONASS time,GLONASST）转化为GPST的计算公式为

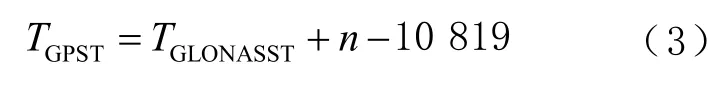
式中：TGLONASST为GLONASS时；n为协调世界时（coordinated universal time, UTC）与国际原子时（international atomic time, TAI）之间不断调整的参数，由国际地球自转服务组织（International Earth Rotation Service, IERS）提供。

GPS采用1984世界大地坐标系（world geodetic coordinate system 1984, WGS84）；Galileo采用伽利略地球参考框架（Galileo terrestrial reference frame,GTRF）；BDS采用北斗坐标系（BeiDou coordinate system，BDCS）；GLONASS采用俄罗斯大地坐标框架（Parametry Zelmy1990, PZ90）。由于列车伪距定位的精度为米级，BDCS坐标和GTRF坐标转换为WGS84坐标产生的误差可以忽略不计[12],只需将PZ90坐标转换为WGS84坐标即可,采用布尔萨-沃尔夫（Bursa-Wolf）模型[13]进行PZ90和WGS84间的坐标转换，Bursa-Wolf模型亦称为黑尔默特（Helmert）7参数模型，其计算公式为

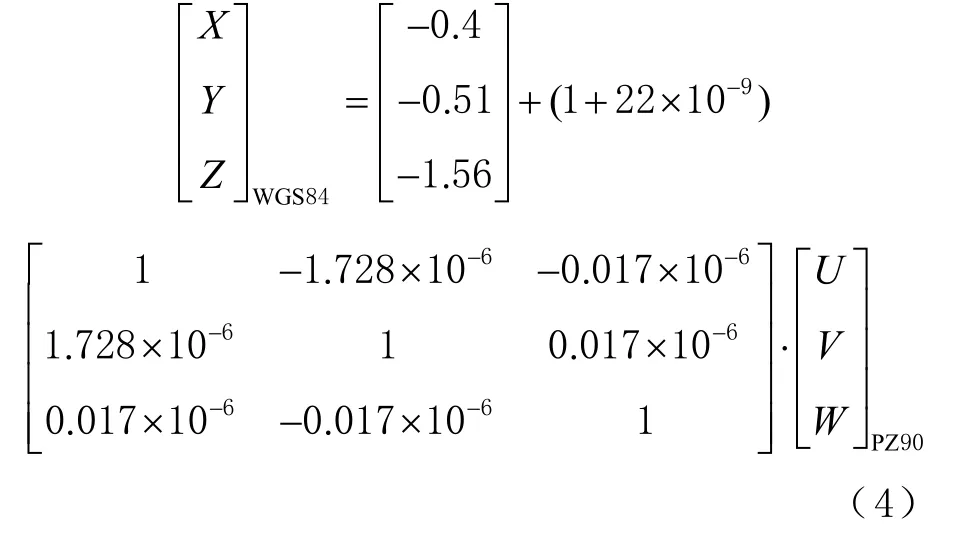
1.2 列车定位原理

在列车运行过程中，可见星连续不断地向车载接收机发送星历参数和时间信息，车载计算机计算出与N颗可见星之间的伪距(ρ1,ρ2,ρ3,…,ρN)，通过联立方程进行列车位置的定位解算，即

式中：ρi(i=1,2,...,N)为第i号卫星到车载接收机的伪距，N为可见星数目；(xi,yi,zi)为第i号卫星的空间位置；(xu,yu,zu)为列车位置；c为光速；tu为车载接收机与卫星间的钟差，其定位原理如图1所示。

图1 列车伪距定位原理

若参与解算的可见星发生故障，会造成ρi的测量值出现偏差，导致列车定位解算结果不准确。因此，需在列车定位解算之前，采用RAIM技术对卫星的健康状况进行判断，剔除出现故障的卫星。

2 基于列车定位的多星座RAIM算法

在列车定位中，RAIM算法采用冗余技术对车载接收机接收到的导航信息进行一致性校验，其本质是通过增加可见星数目来增加信息冗余，实现对卫星的故障检测[14]。当列车导航系统至少监测到4颗卫星时，可进行用户位置的定位解算；至少监测到5颗卫星时，可实现故障卫星的检测；至少监测到6颗卫星时，可对故障卫星进行识别。因此，可见星数目对 RAIM 算法的可用性有很大影响，通过采用多星座系统增加可见星数目进而改善几何分布情况对 RAIM 算法的可用性会有相应提升[15]。

在铁路沿线中，海拔较高时，会使部分卫星的检测效果变差[16]，影响算法的可用性。多星座组合系统通过增加线路中可见卫星数目增加冗余观测信息，进而提高 RAIM 算法在列车定位中的可用性。当车载接收机监测到的可见卫星数N＞n时（n=4+m，m为星座数），可进行故障卫星的检测与识别。对于单星座系统至少监测到n=4+1=5颗卫星；对于双星座系统至少监测到n=4+2=6颗卫星；对于三星座系统至少监测到n=4+3=7颗卫星；以此类推。图2为多星座 RAIM算法的程序流程图。图2中n为故障检测所需的最少可见星数。

图2 多星座RAIM算法程序流程

2.1 构造多星座系统观测方程

假设在某一时刻共有N颗可见星，对式（5）进行泰勒展开，并考虑观测误差，线性化后的多星座系统观测方程为

式中：y∊RN×1为观测伪距与计算伪距的差值；x∊Rl×1为列车的三维位置信息和m个星座对应的时钟误差参数，l=m+3；ε∊RN×1为观测伪距噪声矢量，服从均值为 0，方差为的正态分布。H∊RN∙l为N ∙l维的观测矩阵，其表达式为

式中：A为列车与卫星之间的方向余弦值；B为对应的各星座车载接收机钟差；Aij(i=1,…,m,j=1,…,3)为对应第i个星座观测矩阵Ai的第j列元素，Ai可表示为

2.2 基于奇偶矢量法的故障卫星检测识别

假设伪距误差ε=O，则系统的线性化观测方程为

将系数矩阵H分解成

式中：Q是N∙N阶的正交矩阵；R为N∙l阶的上三角矩阵；O为零矩阵。

将式（10）代入式（9）并左乘QT，可得

式中，QT和R可分别表示为

式中：Qx为QT的前l行，Q为QT的后N-l行；Rx为R的前l行，O是R的后N-l行，为零矩阵。

将式（12）代入式（11）中可得

可得最小二乘解

若考虑到观测误差ε，即y=Hx+ε ，则有

式中：p为奇偶空间上的奇偶矢量；Q为奇偶空间矩阵；奇偶空间矢量p是由ε在奇偶空间矩阵Q上投影所得，可反映故障卫星偏差量等信息。因此，可基于奇偶矢量p构造检测统计量，进行故障卫星的检测识别。

卫星伪距残差向量平方和为v=pTp。根据统计分布理论，当伪距噪声矢量ε中的各个分量相互独立，且服从均值为 0，方差为的正态分布时，v/服从自由度为N-l的中心X2分布；均值不为0时，v/服从自由度为N−l的非中心χ2分布，非中心参数为λ，即

构造检验统计量ri为

式中：ri为第i颗卫星的检验统计量；Qi为第i颗卫星的奇偶空间矩阵。

已知误警率PFA，则有

式中：P(ri＞Tr)为检测统计量大于检测门限的概率，为标准正态分布的概率密度函数。

根据式（18）可求出检测门限Tr，将每个检测统计量ri与Tr进行比较，若ri＞Tr，说明第i颗卫星出现故障。

2.3 多星座RAIM算法可用性判断

为保障列车定位结果的可靠性，在可见星数目达到要求后，还需对沿线可见星的空间几何分布进行预测，对RAIM算法的可用性进行判断。

本文采用水平保护级（horizontal protect level，HPL）THPL来判断RAIM可用性。根据车载接收机接收到的列车定位数据计算THPL值，当THPL小于水平告警阈值（horizontal alert limit，HAL）THAL时，算法可用，反之则无效，车载需重新接收卫星信号进行可用性判断。

利用最大特征斜率Lmax乘以临界偏差Pbias计算出THPL的值。首先，计算每颗卫星的特征斜率为

式中：Li为第i颗卫星的特征斜率；G1i、G2i分别为矩阵G中元素，G= (HTH)−1HT；S为矩阵ii S的对角元素，S=I− (HTH)−1HT。

然后根据检测门限Tr，基于漏检概率PMD计算出临界偏差Pbias=σ0.， λ的计算方法为

水平保护限值可由式（21）计算出，即

式中，SHPL为计算出的水平保护限值。

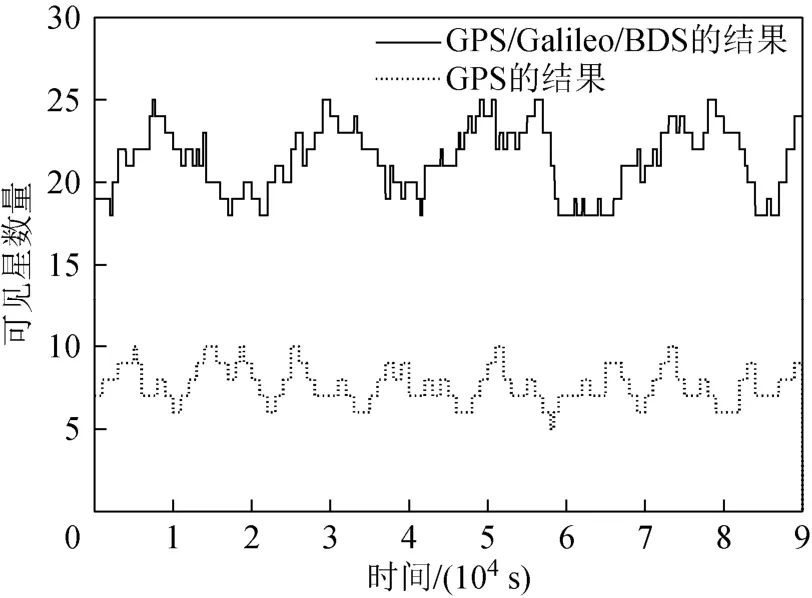
将SHPL与HAL进行比较，若SHPL

3 多星座RAIM算法仿真分析

利用矩阵实验室（matrix laboratory, MATLAB）软件对算法进行仿真分析，本次实验选用 GPS、Galileo和BDS三星座系统。首先根据3个星座系统的卫星及轨道信息参数，对星座进行模拟，模拟中选择24颗GPS卫星，24颗Galileo卫星和14颗BDS卫星，选择列车用户位置在青藏铁路某段线路的固定位置处，用户观测卫星的高度截至角为15°。

3.1 多星座RAIM算法可用性验证

首先对多星座系统和单星座系统下的可见星数量进行仿真对比。图3为GPS/Galileo/BDS多星座系统与GPS单星座系统在某天同时刻下可见星数量的对比情况。由图3可知，在24 h内的任意时刻，多星座系统的可见星数量均高于单星座系统，由于多星座系统增加了卫星数量，所以在相同路况下，可见星的数量也随之增多。随着可见星数量增多，更容易满足 RAIM 算法对冗余观测信息的需求，在列车运行中的某些特殊路段，如城市、山川，多星座 RAIM 能够更好地保障导航信息的连续性和完好性。

图3 可见星数量对比

图4为 GPS/Galileo/BDS多星座系统和 GPS单星座系统在 24 h内对应的位置精度因子（position dilution of precision, PDOP）曲线。

图4 位置精度因子曲线对比

由图4可知，多星座系统各时刻的位置精度因子均小于GPS单星座系统，说明多星座系统能够有效改善可见星几何分布的情况，进而提高算法的可用性。

图5表示青藏铁路某段中密度线路在GPS/Galileo/BDS多星座系统和 GPS单星座系统下的SHPL值对比情况。

图5 SHPL对比

根据铁路领域完好性水平要求，中密度线路的水平告警阈值为20 m[17]。由图5可知，GPS单星座系统SHPL值的波动范围为11.2~27.0 m，多星座系统SHPL值的波动范围为6.0~18.7 m，在34 min之后，GPS单星座系统的SHPL开始出现大于水平告警阈值的情况，发生虚警现象。多星座系统的SHPL值始终小于水平告警阈值，未出现虚警，且在同一时刻，多星座系统的SHPL值均小于 GPS单星座系统，说明列车在相同运行路况下，多星座组合RAIM算法的可用性比GPS单星座系统更好。

3.2 多星座RAIM算法故障检测识别

本次实验所用数据为无故障卫星时的列车定位数据，需通过人为给卫星注入伪距偏差来模拟卫星出现故障，进而对算法进行验证。选用线路数据中几何构型较好的21颗无故障可见星，依次编号为1号至21号，其中：1号至8号为GPS卫星；9号至16号为Galileo卫星；17号至21号为BDS卫星。设定误警率P= 1 × 1 0−6，漏警率P= 1 × 1 0−6，FAMD假设各导航系统的伪距观测噪声水平相同，取σ0=5 m 。

在第80—120秒的时间间隔内，给9号卫星注入60 m的持续故障，其结果如图6所示。

图6 持续故障检测

由图6可知，在第80—120秒的时间间隔内，检测统计量超出了预设阈值，算法检测出了卫星出现持续伪距偏差。

在第20—80秒的时间间隔内，给第17号卫星注入0~60 m的慢变斜坡故障，其结果如图7所示。

图7 慢变斜坡故障检测

由图7可知，在第32秒时，检测统计量超出阈值，检测到有故障发生。随着伪距偏差的增大，检测统计量也不断增大，算法检测出了卫星出现慢变斜坡伪距偏差。

通过故障识别算法得到两种故障情况下各卫星的检测统计量如表1所示，检测统计量最大的卫星即为故障星。

表1 各星座系统卫星检测统计量的值

由表1可知，在持续故障情况下，9号卫星的检测统计量最大，为算法识别出的故障星。在慢变斜坡故障情况下，17号卫星的检测统计量最大，为算法识别出的故障星。算法有效识别出了在持续故障和慢变斜坡故障两种情况下预设的故障星。

3.3 多星座RAIM算法检测性能分析

为检验多星座 RAIM 算法的检测性能，利用3.2节列车定位数据对算法的故障检测率和故障识别率进行仿真分析。

给某颗卫星注入 0~200 m的伪距偏差，采样时间为24 h，采样间隔1 min，仿真结果如图8和图9所示。

图8 故障检测率对比

图9 故障识别率对比

由仿真结果可知，当伪距偏差达到100 m时，多星座系统的故障检测率和故障识别率均可达 100%，而对于GPS单星座系统当伪距偏差达到136 m时，故障检测率才达到100%，伪距偏差达到160 m时，故障识别率才达到94.1%。表明多星座组合RAIM的故障检测性能优于GPS单星座RAIM。

4 结束语

本文利用多星座组合RAIM技术，实时检测接收机自身以及卫星故障，进而提高列车运行过程中定位的精度。在列车定位过程中，采用多星座系统可在相同路况下获得更多的可见星，从而提高RAIM算法的可用性及信息冗余度。在故障检测部分，利用奇偶矢量法计算量少、检测速度快的优势，可实现故障卫星的快速检测。结合青藏铁路列车定位数据分别从算法可用性、故障检测识别和检测性能三个方面进行了仿真分析。结果表明，多星座 RAIM 算法的可用性较单星座系统更好，且能迅速地检测出定位过程中出现的故障卫星，并予以识别。由于信息冗余度的增加，多星座系统的故障检测率和故障识别率较单星座系统均有所提高，位置精度因子较单星座系统有明显的降低。多星座RAIM技术可有效提高列车定位精度，保证铁路运输行车安全。