基于子阵协方差矩阵的线列阵扩展
2022-06-10毛卫宁钱进
毛卫宁, 钱进
(东南大学 信息科学与工程学院, 江苏 南京 210096)
0 引言
阵列信号处理技术广泛应用于雷达、通信、声呐等众多军用和民用领域,是这些领域中的一个焦点问题。信噪比是影响阵列信号处理性能的一个关键因素。对于物理孔径给定的阵列配置,如何提高低信噪比下弱目标的探测性能是工程应用中亟待解决的问题。利用阵列扩展技术,在不增加硬件成本的情况下,通过虚拟增加阵元数目提高低信噪比下弱目标的探测性能,不失为一种有效途径。
目前,一维线列阵阵列扩展方法主要有基于线列阵的旋转不变性和信号非圆对称性的阵列扩展方法、最小二乘和最小一乘法,以及基于互质阵列的阵列孔径扩展方法。基于线列阵旋转不变性和基于接收信号非圆特性的线列阵扩展方法,前者可在阵列扩展的同时实现相干信源的解相干,但在低信噪比条件下鲁棒性较差,后者要求入射信号具有非圆对称性,应用中有局限性。最小二乘阵列扩展法通过处理真实阵元接收信号来估计虚拟阵元接收信号。由于实际海洋环境中的噪声较为复杂,而最小二乘法稳健性较差,使信号估计误差增大。利用最小一乘法估计回归系数稳健性好的特点,文献[11]实现了基于最小一乘稳健估计的虚拟阵元波束形成,但最小一乘法求解比较困难。上述方法均存在扩展阵元的噪声与物理阵元的噪声相关问题,影响高分辨波达方向(DOA)估计性能。基于互质阵列的阵列孔径扩展方法通过建立互质阵列接收信号1阶统计量和增广虚拟阵列2阶等价信号之间的关系,利用空间平滑方法得到增广虚拟阵列所对应的满秩协方差矩阵,并结合多重信号分类处理实现互质阵列超分辨DOA估计,大幅度地提升算法自由度,有效解决了信号数大于阵元数的信号DOA估计问题。但空间平滑方法导致虚拟阵列孔径减小,并且非连续部分的虚拟阵元在平滑过程中被忽略,增广虚拟阵列的信息没有得到充分利用,互质阵列的非均匀性及其信号模型的匹配问题有待进一步研究解决。基于信源和接收信号特性重构阵列数据的二维阵列扩展方法在阵列扩展的同时可以消除噪声的影响,提高DOA估计性能,但主要应用于L型阵列等特殊的二维阵列,如何将该方法运用于一维阵列模型,有待研究。
针对上述问题,本文研究将线列阵按奇、偶阵元分成两个子阵,利用子阵协方差矩阵和线列阵的旋转不变性重构接收阵列数据,实现一维线列阵的阵列扩展,同时消除噪声的影响,解决现有线列阵扩展方法低信噪比下信号检测与高分辨DOA估计性能下降、鲁棒性差、应用有局限性等问题。
1 信号模型
考虑阵元间距为的2个全向阵元组成的均匀线列阵(ULA),2个阵元分布在正轴上,(<2)个远场窄带、不相关信号以平面波形式入射到ULA上,第个阵元接收到的信号为
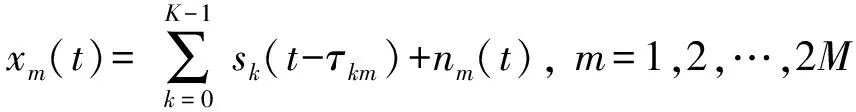
(1)
式中:()为第个窄带源信号;为第个源信号入射到第个阵元时相对于参考阵元的延时;()为第个阵元上的加性高斯白噪声。
(1)式写成向量的形式为
=+
(2)
式中:为2×1维阵列接收信号向量,
=[(),(),…,2()]
(3)
为2×维阵列流型矩阵,
=[(),(),…,(),…,()]
(4)
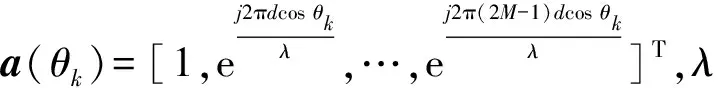
=[(),(),…,()]
(5)
=[(),(),…,2()]
(6)
2 线列阵扩展与DOA估计
利用线列阵阵列流型矩阵的共轭对称性及入射信号的非圆特性,直接在阵元域进行阵列扩展,是常用的线列阵扩展方法,由于扩展阵元的噪声与物理阵元的噪声相关,导致低信噪比时信号检测与高分辨DOA估计性能下降。为解决这一问题,本文研究将线列阵按奇、偶阵元分成两个子阵,利用子阵协方差矩阵重构阵列数据,实现一维线列阵的阵列扩展,并在阵列扩展的同时消除噪声的影响,从而提高弱目标的探测性能。
线列阵按奇、偶阵元分成两个子阵,两个子阵的接收信号分别为
=[(),(),…,2-1()]
=[(),(),…,2()]
(7)
式中:为奇数号阵元构成的子阵的接收信号;为偶数号阵元构成的子阵的接收信号。奇、偶阵元构成的两个子阵接收信号协方差矩阵为
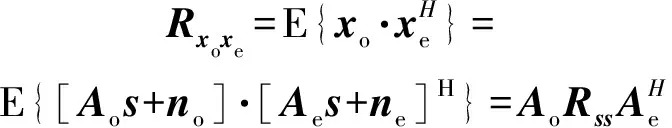
(8)
式中:和分别为奇、偶阵元构成的两个子阵阵列流型矩阵,可分别表示为
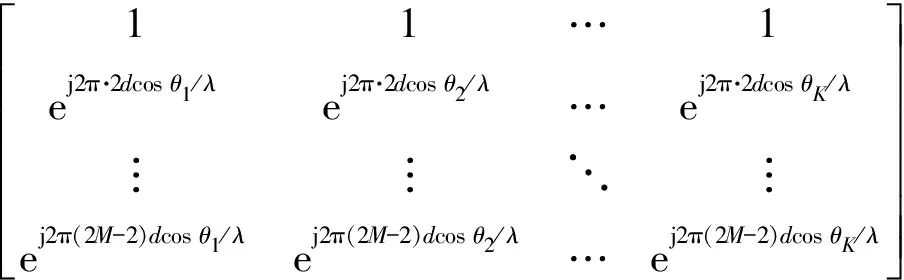
(9)
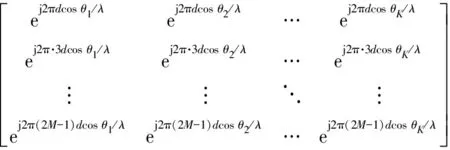
和分别表示奇、偶阵元接收到的噪声信号,分别为
=[(),(),…,2-1()]
=[(),(),…,2()]
(10)
为源信号的协方差矩阵,=E{·},[·]表示共轭转置。
用、表示协方差矩阵的前-1列和后-1列构成的矩阵,则

(11)
式中:和分别代表偶数阵元构成子阵的阵列流型矩阵的前-1行和后-1行对应的矩阵,根据线列阵的旋转不变性=,其中



(12)
扩展接收阵列的信号协方差矩阵为
=()
(13)
在(13)式基础上,利用最小方差无畸变响应波束形成(MVDR)等方法可实现高分辨DOA估计。MVDR的波束输出功率为
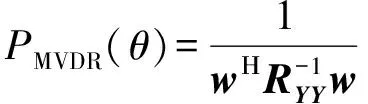
(14)
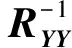
(8)式表明:奇、偶阵元构成的两个子阵接收信号协方差矩阵消除了噪声的影响,因而基于两子阵接收信号协方差矩阵和线列阵旋转不变性的线列阵扩展,可解决阵元域信号直接扩展,扩展阵元接收信号中的噪声与物理阵元接收信号中的噪声相关,导致低信噪比下信号检测和高分辨DOA估计鲁棒性下降的问题;此外,奇、偶阵元构成的两个子阵阵列孔径基本上没有损失,奇、偶阵元构成的两个子阵,变相增大了阵元间距,使处理频带与阵元间距的半波长关系不再满足,但由于是宽带处理,不会引入栅瓣问题,不过两个子阵的接收信号协方差矩阵相比于2×1维阵列接收信号的协方差矩阵,存在信号信息损失,影响极低信噪比下的DOA估计性能;最后,(12)式、(13)式表明,扩展阵列的接收信号协方差矩阵为4×4维,相当于阵列孔径增大了一倍。
3 仿真分析
目标信号为带限噪声,频带2 000~3 000 Hz,采样频率16 kHz,声速1 500 m/s,单次快拍数为1 024,信源数为1。采用阵元数为12的ULA,阵元间距为中心频率波长的一半。
目标方位60°,信噪比-10 dB,比较扩展线列阵与未扩展线列阵的MVDR空间谱,如图1所示。相比于未扩展线列阵,扩展线列阵空间谱平均旁瓣级降低了5 dB以上,噪声抑制能力增强。未扩展线列阵的MVDR自适应波束形成低信噪比时,稳健性下降,空间谱旁瓣升高,本文方法在阵列扩展的同时消除了噪声的影响,解决了扩展阵元的噪声与物理阵元的噪声相关的问题,从而降低了空间谱旁瓣,提高了稳健性,有利于弱目标探测。

图1 扩展线列阵MVDR空间谱Fig.1 Extended line array MVDR space spectrum
信噪比-25~-15 dB,对每个信噪比进行200次独立的仿真测试。测试时,空间谱主瓣高出旁瓣5 dB,认为检测到目标,比较扩展线列阵与未扩展线列阵检测概率随信噪比的变化,如图2所示。由图2可见,由于阵列扩展的同时消除了噪声的影响,显著提高了低信噪比下的检测概率:信噪比-19 dB时,扩展线列阵的检测概率为100%,未扩展线列阵的检测概率为70%;信噪比-20 dB时,扩展线列阵的检测概率为96%,而未扩展线列阵的检测概率为7%。扩展线列阵提高了对弱目标的检测能力。
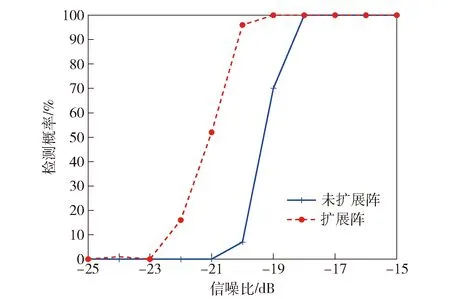
图2 扩展线列阵检测概率随信噪比的变化Fig.2 Change of detection probability of extended linear array with signal-to-noise ratio
目标方位60°,信噪比-25~10 dB,比较本文方法、阵元域扩展方法与未扩展线列阵的DOA估计性能。采用最小方差无畸变响应MVDR波束形成方法进行DOA估计,图3为本文方法、阵元域扩展与未扩展线列阵DOA估计偏差随信噪比的变化,图4为本文方法、阵元域扩展与未扩展线列阵DOA估计均方根误差随信噪比的变化。统计DOA估计偏差和均方根误差时以空间谱最大值对应的方位为目标方位,作为方位测量值。由图3和图4可见:信噪比大于-15 dB时,本文方法与未扩展线列阵的DOA估计性能相当;信噪比低于-20 dB时,本文方法由于存在信息损失,DOA估计性能下降;信噪比-5 dB时,阵元域扩展方法的DOA估计性能较未扩展线列阵有所下降,随着信噪比降低,阵元域扩展方法的DOA估计性能迅速下降。
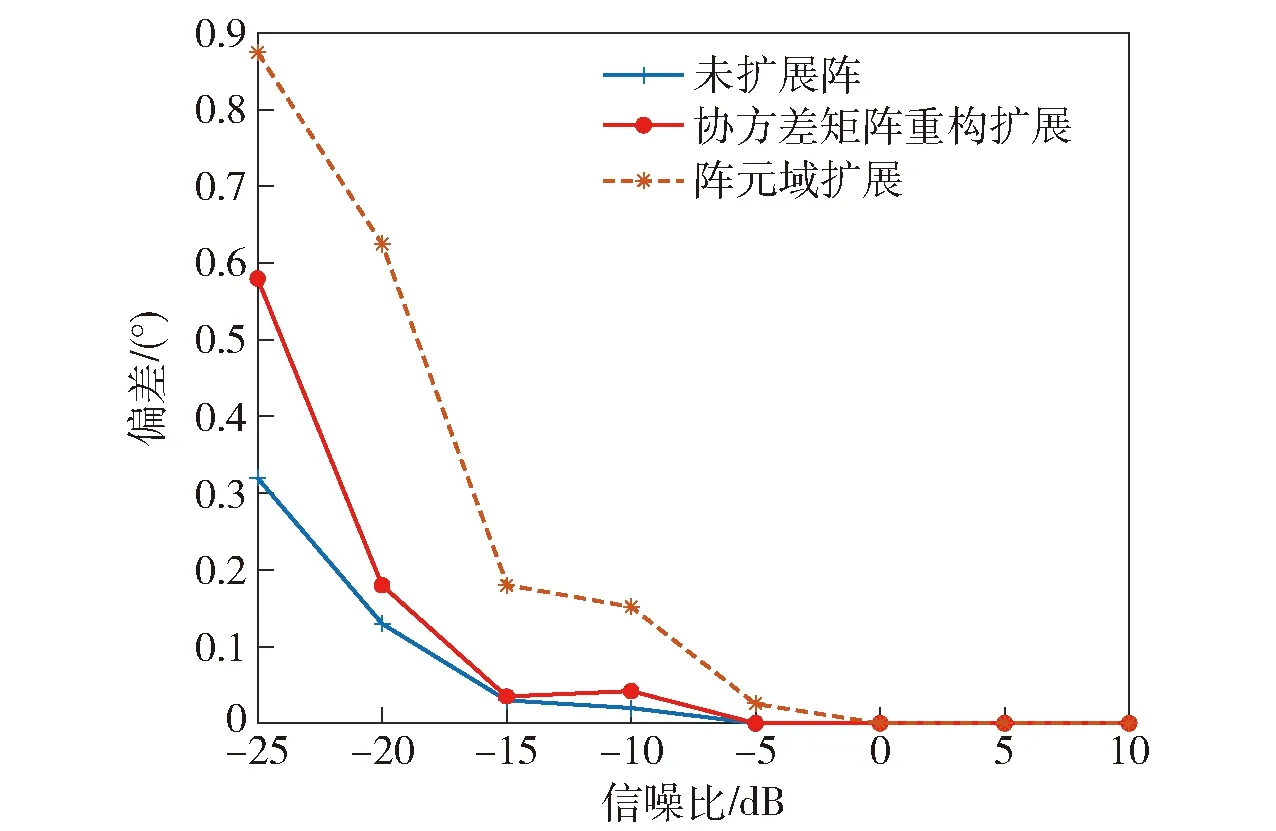
图3 DOA估计偏差随信噪比的变化 Fig.3 Change of DOA estimation bias with signal-to-noise ratio
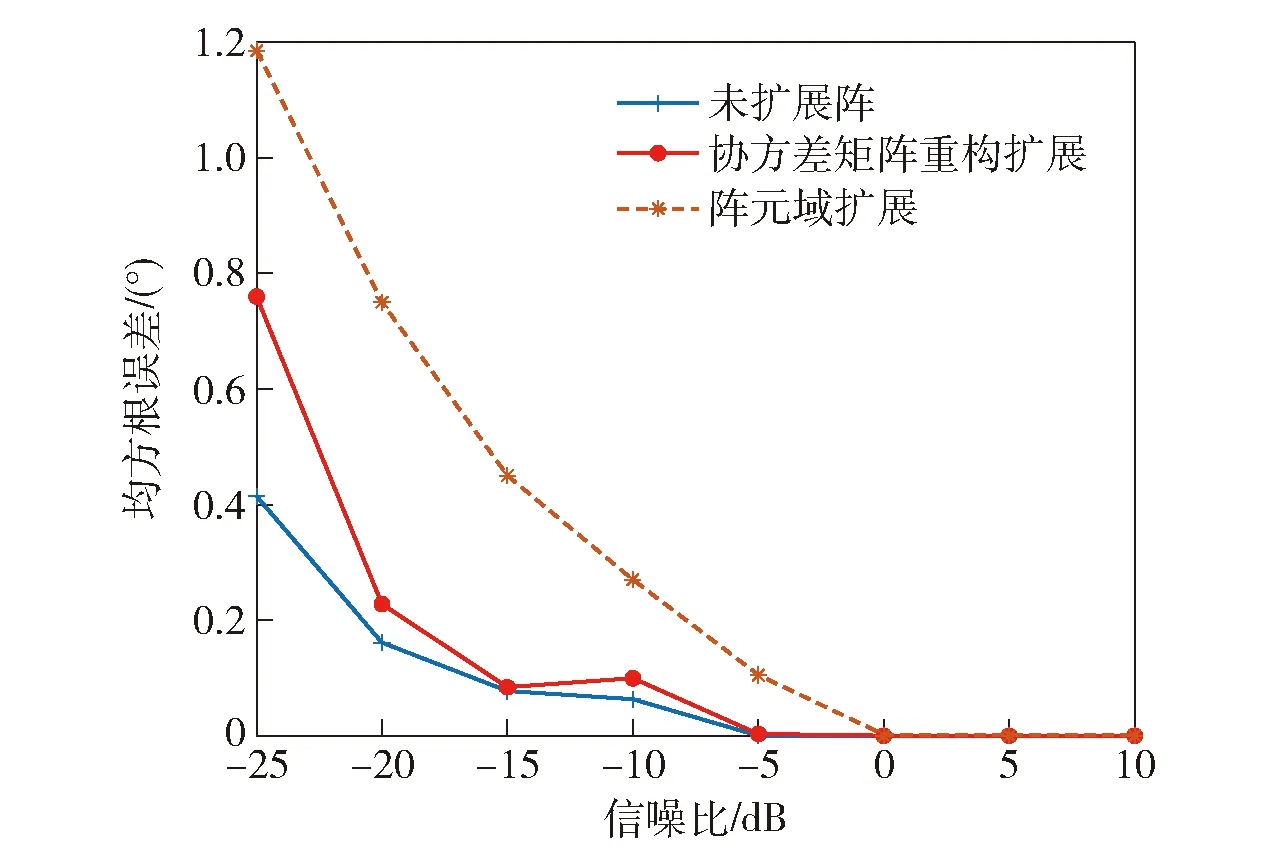
图4 DOA估计均方根误差随信噪比的变化Fig.4 Variation curves of DOA root mean square error of
4 实测数据处理分析
分析处理海上实测数据,以进一步验证本文方法的有效性。接收基阵为ULA,接收信号为带限噪声,单次快拍数为1 024,数据处理结果如图5所示。相比于未扩展线列阵,扩展线列阵空间谱平均旁瓣级降低了约7 dB以上,噪声抑制能力明显增强。

图5 实测数据扩展线列阵MVDR空间谱Fig.5 Extended line array MVDR space spectrum for test data
5 结论
本文提出将线列阵按奇、偶阵元分成两个子阵,利用子阵协方差矩阵及线列阵的旋转不变性重构阵列数据,实现一维线列阵的扩展方法。与线列阵阵元域直接扩展方法相比,本文方法在阵列扩展的同时消除了噪声的影响,降低了波束输出旁瓣,解决了阵元域直接扩展,扩展阵元的噪声与物理阵元的噪声相关,低信噪比下信号检测和DOA估计鲁棒性下降的问题,提高了弱目标的探测性能,具有较好的工程应用价值。
但由于扩展线列阵存在信息损失,极低信噪比下DOA估计性能下降,这一问题有待进一步研究。此外,实际应用中阵元位置可能存在一定误差、各阵元噪声可能存在一定相关性,前者可结合稳健自适应波束形成等方法加以解决,后者会影响本文方法的性能,影响程度取决于噪声相关性的大小。结合去相关处理技术,可减小相关噪声的影响。
