大气- 海雾多层环境下的天空偏振模式

刘阳， 付强， 张肃， 战俊彤， 史浩东， 李英超， 刘艺， 娄岩， 余益欣

(1.长春理工大学 光电工程学院， 吉林 长春 130022； 2.长春理工大学 理学院， 吉林 长春 130022)

0 引言

自然环境的大气特别是以平流冷却雾为主的海洋低层大气，其生成过程是通过一定途径使空气达到饱和，并适当地有些过饱和现象来完成的[1]。由于大气- 海雾环境的存在，非偏自然光通过海雾粒子及大气分子等多层介质散射，使得天空光增加了偏振特性，因此研究复杂海洋环境下的天空偏振分布情况，对海上交通运输、海洋目标探测和海洋开发等领域具有重要意义[2]。

许多研究者对天空光的偏振分布特性在理论与仿真方面都做了一定的研究工作。文献[3]在Reyleigh大气偏振模式的基础上，提出一种太阳和太阳子午线空间位置的计算方法，采用对偏振度(DOP)进行聚类分析的方法确定太阳的位置。文献[4]研究晴朗天气条件下满月天空的偏振模式，以Rayleigh理论为基础，分别采用仿真与测试方法对太阳光和月光天空偏振特性的分布规律进行了研究。文献[5]通过矢量偏振分析装置来获取大气散射光偏振信息，在Mie散射理论的基础上，对大气散射光偏振特性与太阳位置及散射粒子间的关系开展了研究。以上研究都为介绍天空偏振分布模式提供了理论基础，但这些研究多适用于晴朗天气情况。对于雾天等复杂天气情况的研究，多以矢量辐射传输方程作为基本的传输理论，矢量辐射传输方程被认为是描述散射行为的基本方程，它描述了偏振等辐射能在介质中的传输过程、特性以及传输规律[6]。文献[7]采用蒙特卡洛方法仿真不同太阳高度角下水云大气全天空偏振模式，研究了水云条件下光学厚度、有效半径对偏振特性的影响。文献[8]基于倍加累加(RT3)法和T矩阵法计算粒子层散射特性，建立了适用于多种天气条件下的天空光偏振模型。

由于海洋环境复杂多变，目前对于大气- 海雾环境下天空光偏振分布模式的研究相对较少。为了扩展偏振探测的适用范围，本文进一步研究复杂海洋环境垂直观测下天空的偏振分布特性，用简化的大气、海雾双层结构模拟复杂海洋环境，分别由Rayleigh和Mie散射方法求得大气、海雾层粒子分布特性，将每层分布特性代入RT3方法中，仿真不同能见度的海雾环境辐射偏振特性，重点研究太阳子午线上典型可见光波段、太阳位置、观测位置以及能见度等参数变化下偏振下行辐射的变化情况，掌握多层海洋介质环境下垂直方向偏振传输特性的演化规律，为海洋目标高精度成像探测提供理论与技术支撑。

1 基于RT3方法的天空偏振建模

在RT3方法中，根据每层粒子特性，非均匀层可划分为若干均匀薄层，基于矢量辐射传输方程的求解过程，对两层间的多次反射和透射过程进行计算，得到整个非均匀层的辐射和透射特性。

辐射传输方程描述单色辐射量与大气的相互作用以及因此产生的变化，考虑光学厚度τ、单次散射反照率ω和太阳天顶角余弦μ0与方位角φ0等参数的影响，辐射传输方程的一般形式可表示为

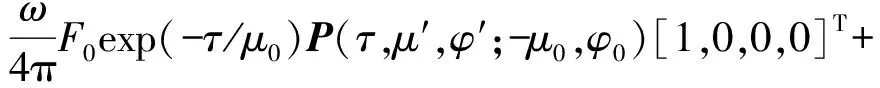
(1)

式中：μ和φ分别为入射天顶角余弦和方位角；μ′和φ′分别为出射天顶角余弦和方位角；I为出射的Stokes矢量；P表示散射矩阵；F0为大气层顶太阳辐射；B(T)为Planck黑体函数。(1)式中等号右端第2项是由粒子的多次散射所引起的，第3项是由上一层边界辐射发生的单次散射，最后一项表示热辐射。

对(1)式中的散射矩阵进一步展开，由相位矩阵F来表征散射矩阵P，

P(θ，φ；θ′，φ′)=R(i2-180°)·F(cosΘ)·R(i1)

(2)

式中：θ为天顶角；θ′为出射光线的天顶角；Θ为散射角；i1和i2分别表示入射光线所在散射平面与子午面的夹角和出射光线所在散射平面与子午面的夹角；R为光相对于参考面与相对于散射面的Stokes矢量之间转换的旋转矩阵，使改变散射前后的参考面一致，

R(i2-180°)=

(3)

(4)

对于旋转对称粒子，相位矩阵F(cosΘ)可表示为

F(cosΘ)=

(5)

式中：fi(i=1，2，…，6)为相位矩阵中各元素不同角度下的相位值，当粒子为球形粒子时有f1=f5，f3=f6。

将相位矩阵F中的元素以勒让德多项式的表达形式代入矢量辐射传输方程中进行求解，相位矩阵中的各元素表示为

(6)

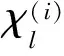
基于RT3方法的矢量辐射传输方程求解过程如图1所示，首先根据各层间温度、消光系数等信息将大气层进行划分；通过每次粒子类型、粒子谱分布和折射率等信息，求解各层的散射特性；然后，将太阳位置、辐射源信息、地表信息和大气分层等输入到基于RT3方法的辐射传输方程中进行计算，得到整个大气层的反射和透射性质，求出全天空各散射点的Stokes矢量分布。

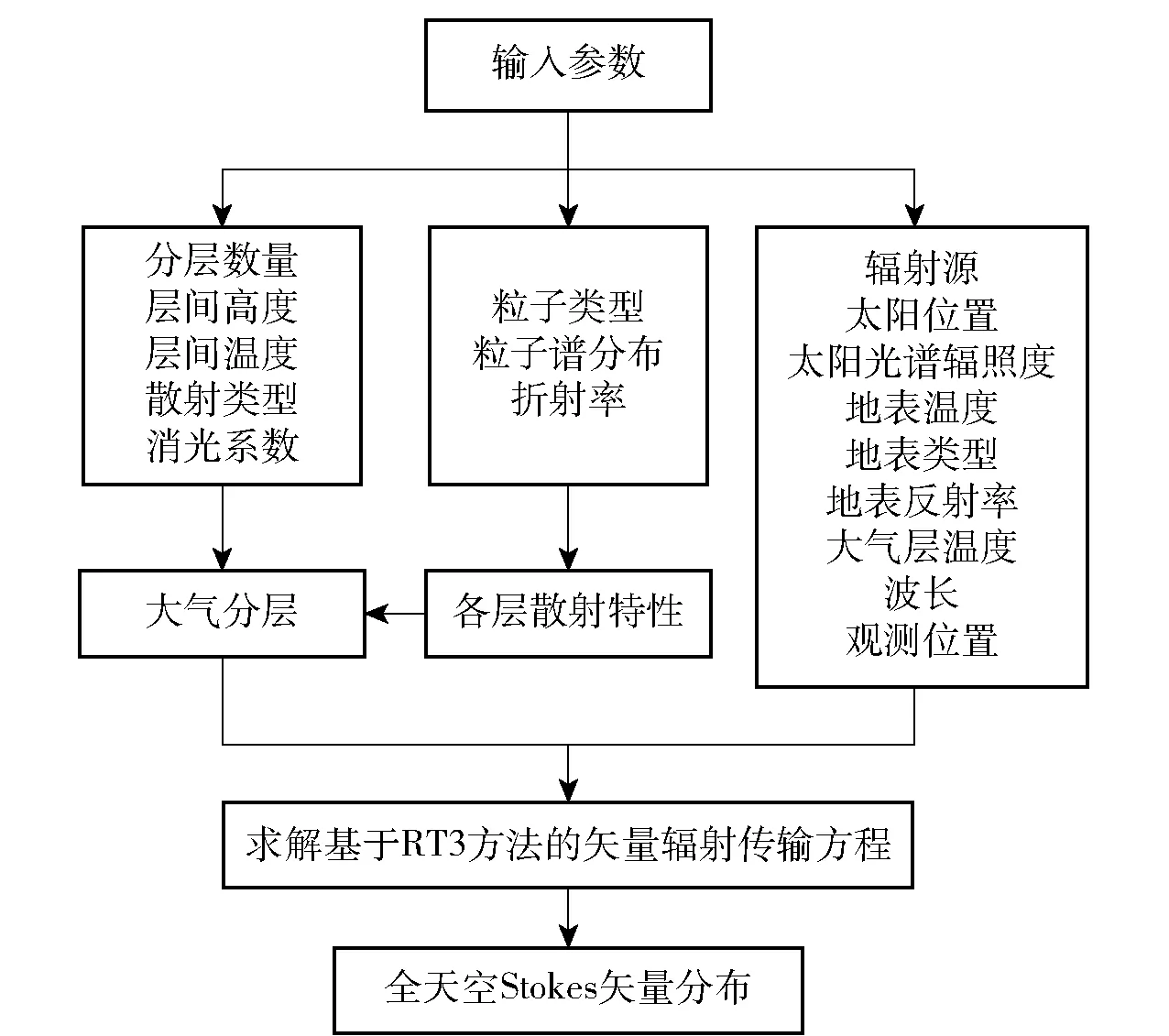
图1 基于RT3方法的矢量辐射传输方程求解过程Fig.1 Solution process of vector radiation transmission equation based on RT3

2 大气- 海雾复杂环境的多层粒子分布特性

2.1 大气- 海雾复杂环境的分层

海洋环境根据雾的浓度不同可被视为多层的复杂介质，包括大气层以及能见度逐渐减少的海雾层，由于根据实际海面上海雾天气的情况对大气- 海雾环境进行划分时需要考虑的情况及其复杂，为简化计算，参考美国标准大气模式[9]，根据每层散射粒子和所含水汽的不同，在晴朗情况下将整个大气- 海雾环境划分为均匀的两层，即海雾层和大气层[10]，如图2所示，其中5～15 km的大气层水汽含量较少，主要发生的是Rayleigh散射，0～5 km的海雾层粒子直径较大，散射过程复杂，主要由Mie散射进行计算。

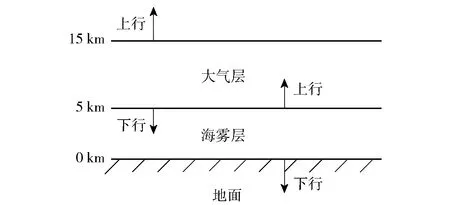
图2 大气- 海雾环境分层情况Fig.2 Stratification of atmosphere and sea fog environment

2.2 海雾层粒子分布特性

海雾层粒子尺度分布受地域、天气、时间等因素共同作用，雾滴粒子通常可用应用最广的Gamma分布模型[11]描述为

n(r)=ar2e-br

(7)

式中：n(r)为粒子分布函数，r为雾滴粒子的半径；a和b分别为雾滴谱的形状参数，与含水量W(g/m3)和能见度V(km)有关，分别表示为

(8)

在海雾环境，平流雾在海雾中范围较大，浓度较重，在海雾环境中占较大比例。对于平流雾，含水量与能见度具有以下关系：

W=(18.35V)-1.43=0.015 6V-1.43

(9)

则可得海雾粒子粒径分布与能见度的关系：

n(r)=1.059×107V1.15r2e-0.835 9V0.43r

(10)

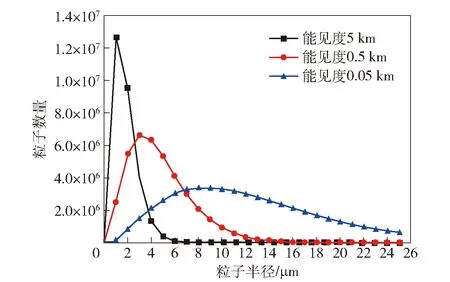
图3 3种不同能见度下海雾粒子粒径分布情况Fig.3 Size distribution of sea fog particles under three different visibilities

假设海面雾层分别由浓雾、中雾及轻雾组成，分别选取典型能见度为0.05 km、0.5 km和5 km，代入(10)式中，可分别得到浓海雾、中海雾及轻海雾的粒子粒径分布，如图3所示。则满足修正Gamma分布的3种不同浓度的浓海雾、中海雾及轻海雾的模半径分别为8.676 μm、3.223 μm和1.198 μm。

3 大气- 海雾偏振仿真结果与分析

3.1 海雾层粒子的散射特性

根据海雾层分布特性可确定浓雾、中雾及轻雾满足修正Gamma分布下的各参数。对于均匀、同性、球形的海雾粒子，为研究不同浓度海雾粒子对偏振光散射特性的影响，根据Mie散射理论，求解(2)式中第1项，即散射相位函数与散射角的关系，如图4所示。从图4中可以看出：在前向几度的小角度内，散射光表现得十分非常集中，与其他方向的散射光相比，高出大概4个量级；随着能见度的降低，即海雾浓度的增大，散射相位函数不断增大，使整个散射环境趋于前向散射。由此可见，对海雾层中粒子散射特性的研究可为大气- 海雾天空偏振模式分布的研究奠定理论。

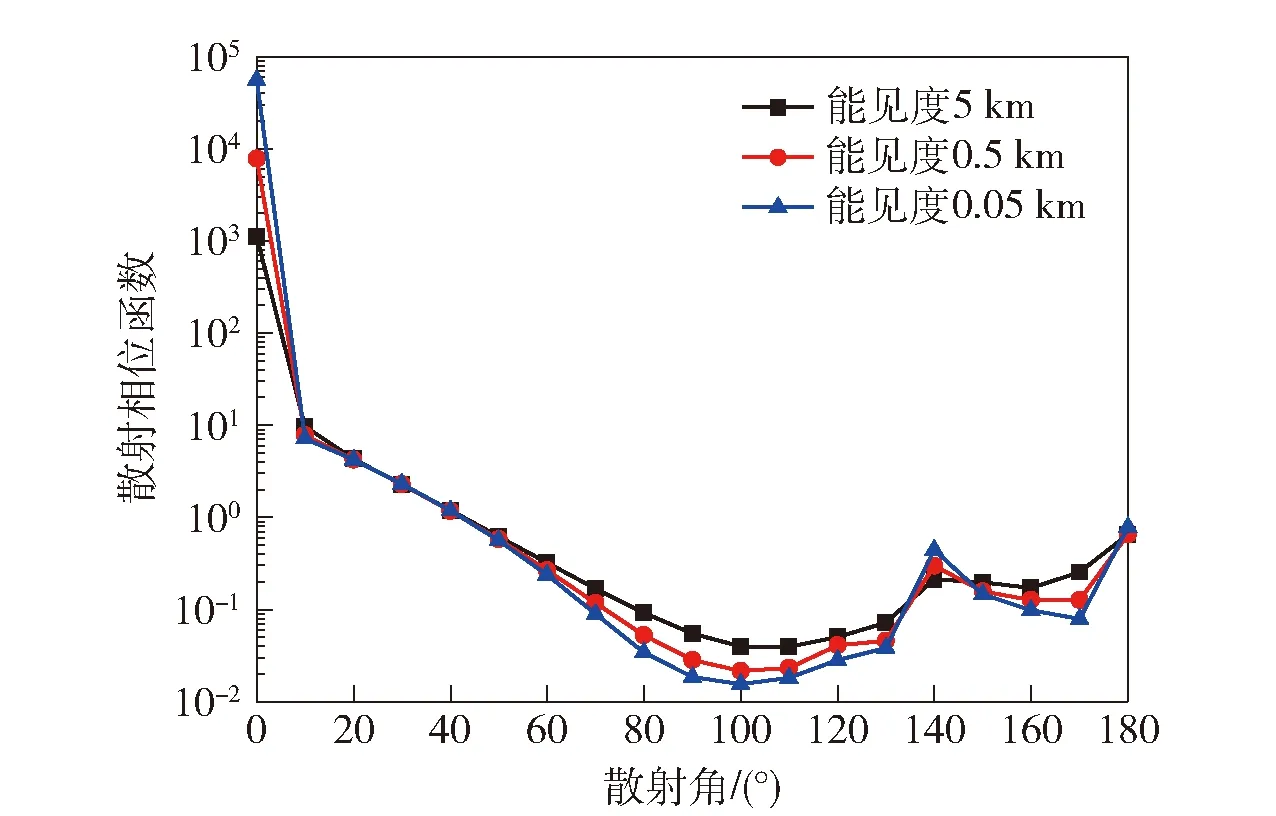
图4 散射相位函数与散射角的关系Fig.4 Relationship between scattering phase function and scattering angles

3.2 大气- 海雾天空偏振模式

为更真实地模拟海雾环境，根据3.1节中对大气- 海雾复杂环境分层情况的描述，将其分为两层，其中太阳天顶角为60°，方位角为0°，地表为朗伯地表类型，并且反射率为0，温度为300 K，海雾层根据能见度的不同，可得到相应修正Gamma分布下的模半径(见2.2节)，相对折射率为1.333+1.96×10-9。由于天空光的偏振探测多采用可见光波段，在可见光波段下分别选择测试中常用的典型波长450 nm、532 nm和671 nm进行仿真，根据前期研究基础，选择经过太阳与天顶的子午线位置，由于大气散射天空偏振分布关于太阳子午线位置对称，研究浓海雾、中海雾以及轻海雾不同环境下的太阳子午线上DOP与观测高度角的变化关系。

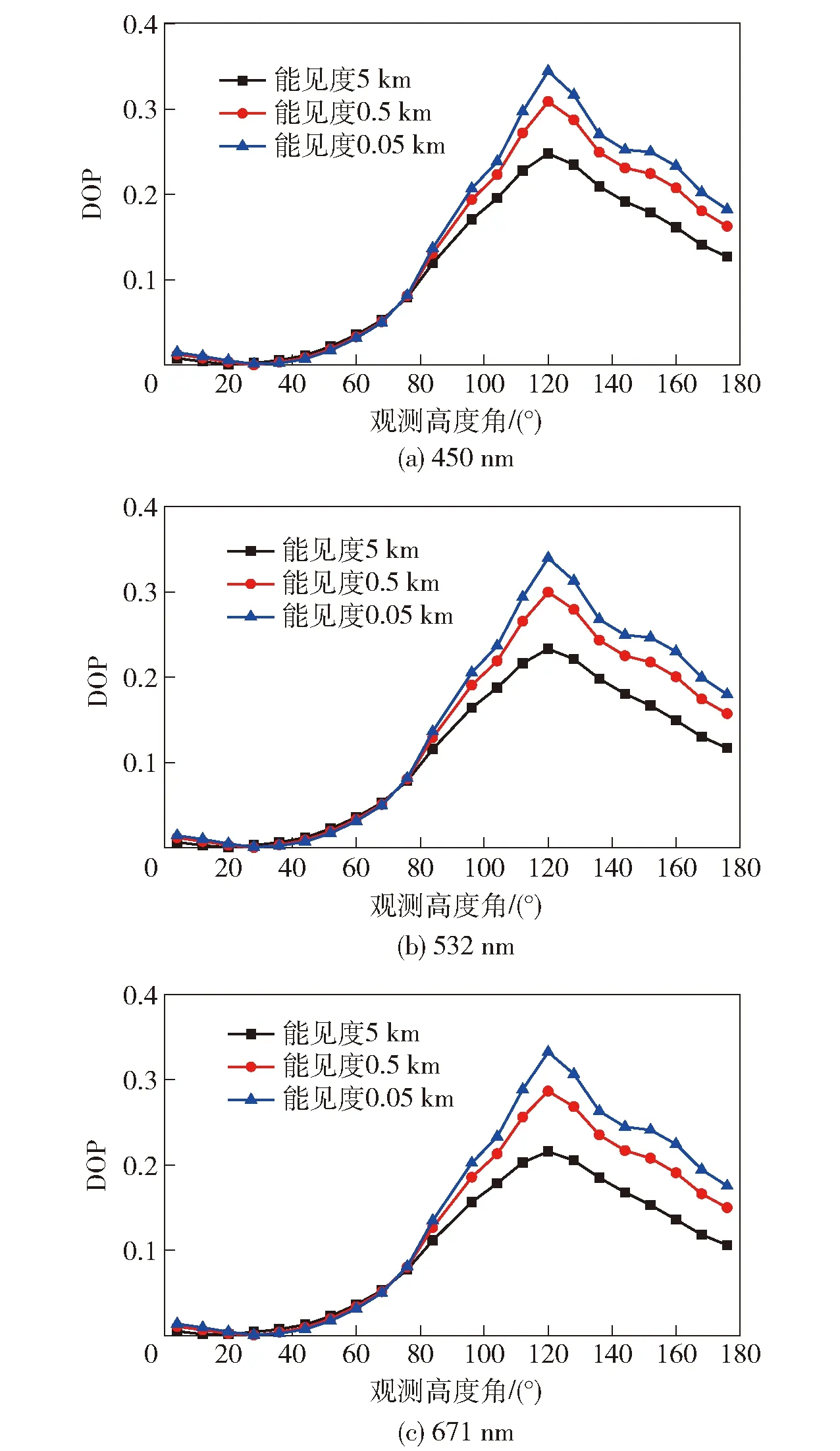
图5 不同能见度下DOP与观测高度角的变化关系Fig.5 Relationship between DOP and observed altitude angle under different visibilities

图5所示为3种波长下不同能见度下DOP随观测高度角的变化关系。由图5可见：3种能见度海雾下DOP的变化趋势基本相同，都在观测高度角等于太阳高度角30°时，DOP取得最小值，数值接近于0；当观测高度角与太阳高度角夹角为90°时，可得到最大DOP，这一现象与基于Rayleigh散射的大气理论模型得到最小值与最大值的位置相对应[12-16]；随着能见度的逐渐减小，DOP值逐渐增大，这是因为当能见度减小时粒子平均半径增大(见图3)，粒子尺寸增大会导致DOP的值增大[17-18]，且浓海雾中粒子个数的增加会导致散射次数的增加，使得无偏的太阳光经更多次数的散射后转化为偏振光的几率增大[19-21]，因此DOP随能见度的减小会逐渐增大，且这一现象随观测角的增加越来越明显；当观测高度角较小(小于90°)时，即太阳高度角与观测高度角所成的散射角较小时，DOP对粒子形状的依赖性较弱，则DOP情况基本相同。对比3种不同波长下的仿真情况，均可得到相同的变化趋势。

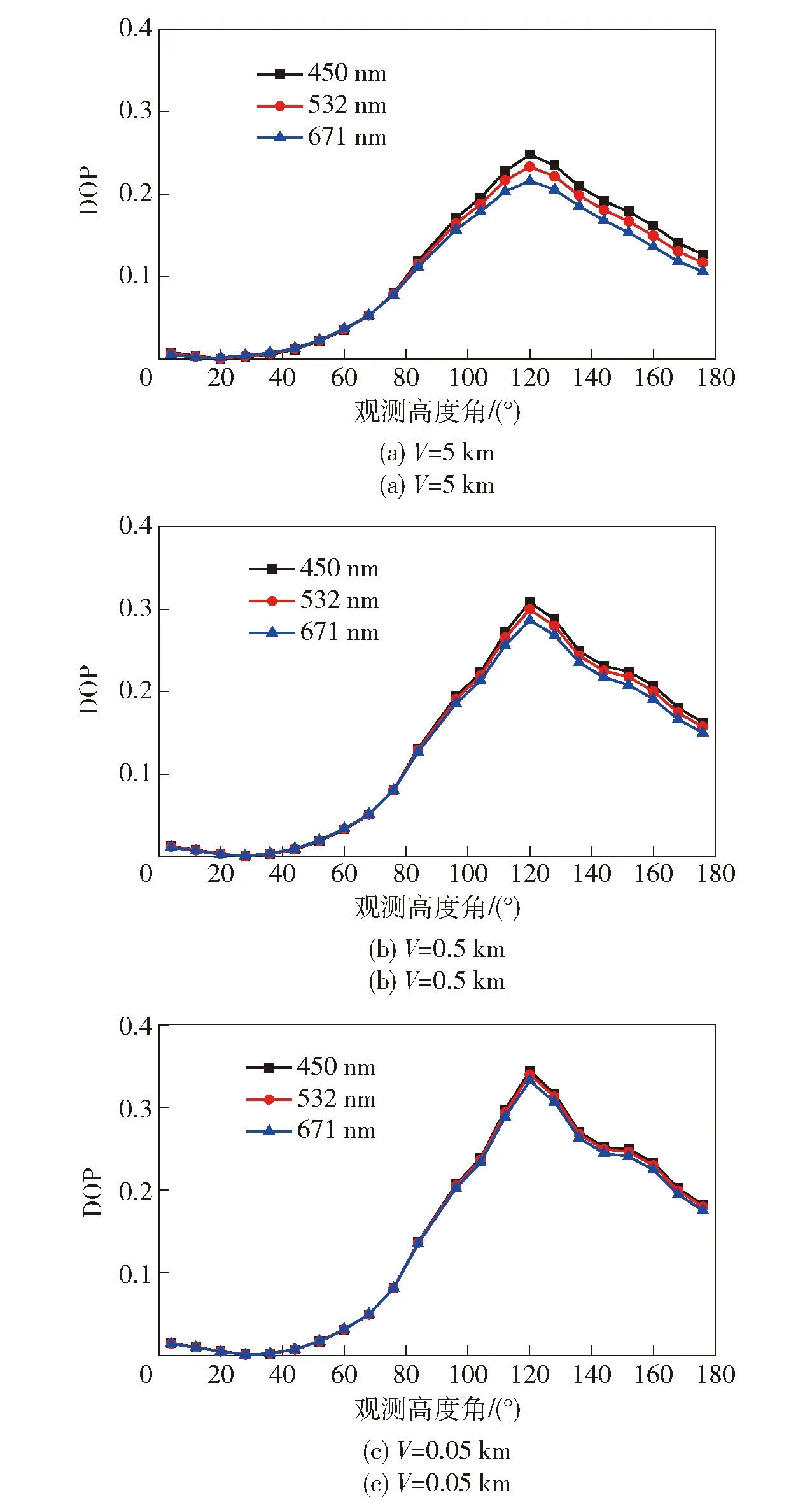
图6 不同波长下DOP与观测高度角的变化关系Fig.6 Relationship between DOP and observed altitude angle under different wavelengths

图6所示为3种能见度下典型可见光波长下DOP随观测高度角的变化关系。由图6可见：同一能见度下随着波长的增加DOP逐渐较小，与粒子尺寸参数x=2π/λ有关，当波长λ增大时粒子尺寸参数x减小，抑制前向散射光的集中，从而DOP减小，散射相位函数与散射角的关系(见图4)也很好地解释了这一现象，从另一方面验证了图5中所得到的结论。随着能见度的减小，介质中粒子半径不断增大，导致波长对尺寸参数的影响越来越小，对比图6(a)～图6(c)可知，波长对DOP的影响越来越小，最后在浓雾中的偏振特性基本趋于一致。

在实际试验中，在室内拟搭建多层海雾环境模拟系统，采用白光模拟非偏太阳光，建立半实物模拟环境，确保测试的稳定性；在室外拟采用光谱仪结合偏振片探测的方式，在海面进行探测某一观测点的下行辐射值，与实际仿真结果进行验证。但由于海面环境受海雾、海浪等多种条件限制，给大气- 海雾环境天空偏振模式的测试带来了难度，这也是本文研究下一步具体的研究工作。但通过该模拟结果的理论分析，以及与晴朗天气下经典Rayleigh散射模型的对比，也可证明该模拟结果的正确性，可为大气- 海雾多层环境下的天空偏振模式测试研究奠定理论基础。

4 结论

本文将复杂海洋环境简化为大气、海雾双层结构，采用倍加累加方法计算两层介质间的辐射传输，得到全天空偏振分布情况，具体给出太阳子午线上海雾层下行辐射的偏振分布情况。得出主要结论如下：

1) 在太阳与观测高度角间的散射角90°时，可得到最大DOP值；相反地，在太阳位置处，可得到最小DOP值。

2) 随着能见度的下降，DOP逐渐增加，且这一现象随观测角的增加(观测高度角大于90°)越来越明显

3) 对于可见光典型波长(450 nm、532 nm和671 nm)，随波长的增大，DOP逐渐减小，而且能见度逐渐降低，波长对偏振特性的影响越来越小。

为了验证仿真结果，考虑以舰载方式搭建测试设备，使垂直方向的海雾传输依次经过偏振片、光谱仪等仪器，最后测试不同太阳位置及不同观测位置下的天空偏振特性情况。但由于实际环境中海雾环境复杂且轮船抖动等多种外部原因，需要大量环境测试等工作，下一步将重点研究该测试试验。