基于共轭梯度法辨识钢渣温度分布
2022-06-09翟恒东李利民杨骏霍玉峰邓思洪蒋麒麟
翟恒东 李利民 杨骏 霍玉峰 邓思洪 蒋麒麟
(1:中冶宝钢技术服务有限公司 上海 200999;2:武汉科技大学冶金装备及其控制教育部重点实验室 湖北 武汉 430081;3:武汉科技大学机械传动与制造工程湖北省重点实验室 湖北 武汉 430081)
1 前言
渣罐是在冶金环节完成之后用来放置剩余高温炉渣的容器,是冶金企业生产过程中的关键设备之一。钢渣在生产后一直放在渣罐中进行冷却,是非常珍贵的二次资源,由于钢渣中不同金属离子结晶析出所需要的温度不同,因此钢渣的温度对其回收率有着直接影响[1-3]。目前测温方式主要分为两类:机械类测温和辐射测温。但机械类测温读数无法稳定,且需要人工现场操作电子探枪,危险系数极高;辐射测温基于红外线进行测温,器件不需要接触热源,但此类方式易受外界干扰,测量精度无法保证。
由于传统测温方法存在较大弊端,大部分学者开始将反问题的理论和思想应用于传热学研究中,通过反演方法对钢渣温度进行间接测量。Fan Yang[4]等人通过Tikhonov正则化方法成功解决了利用抛物线方程求解热源反问题时的不适定性。吴洪潭[5]采用正则化思想研究了非稳态一维线性传热反问题,提升了研究结果的准确率。Joanna Wrobel[6]等人利用神经网络算法对焊接加热生产时的热处理过程进行了反向分析,且获得理想结果。Hua Wang[7]等人提出了一种利用人工神经网络求解热传导逆问题的新方法,该方法已成功地应用于具有接触间隙导热传热的背杆传热模型。刘枭[8]等人运用谱共轭梯度法成功得到了更加真实的地下形态。卓立军[9]等人将温度测量数据作为热源大小识别的反问题模型的输入参数,使用共轭梯度法研究了烧蚀材料的热学参量表征。余远锋[10]等人解决了二维空间跟着坐标变换的接触热阻的困惑,证实了反演结果与真实接触热阻吻合。马晓波[11]等人基于共轭梯度算法探究了材料亚表层缺陷深度。但目前还未见对渣罐内钢渣温度分布进行反演的研究。
本文基于传热学反问题,以渣罐外壁温度为已知信息对冶金渣的温度散布状况进行反演。通过创建渣罐传热数学模型,分析不同时刻钢渣温度分布情况。并运用共轭梯度法(CGM),以局部测量壁温为输入值,对渣罐内钢渣温度散布进行反演。该方法避免了传统测温方法成本高以及精度不足的问题,为研究钢渣温度分布提供了新思路。
2 正问题
2.1 数学模型
考虑到渣罐的实际部件构造较多,渣罐内是熔融状态下的熔渣,钢渣处理时的工序也比较繁琐。对某12m3的钢渣罐工作开展以下简化与假设:
(1)忽略圆周方向的换热,将渣罐的传热看作二维层面;
(2)图1为简化后的正问题钢渣罐模型。按照钢渣罐的对称性取图1所示的阴影部分作为分析对象;
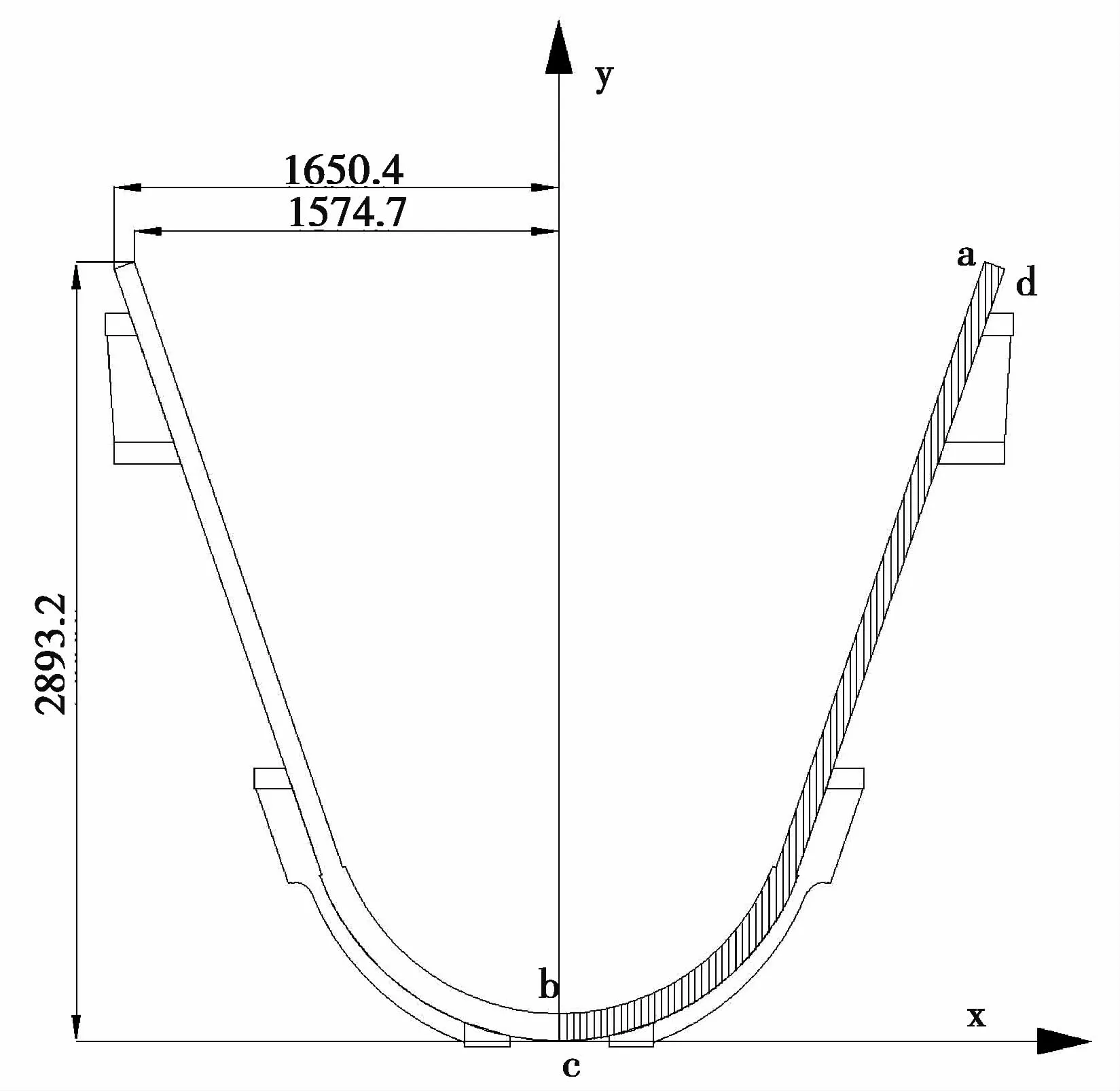
图1 简化渣罐模型
(3)忽略渣罐与钢渣的接触热阻;
(4)钢渣比热容不随温度变化;
(5)温度较高的渣罐罐壁因为和空气的热对流和热辐射,其温度下降较快;
(6)渣罐上沿与外部环境接触面积较小,散热量较小,忽略其导热作绝热处理。
2.2 简化钢渣罐的数学模型
在以上简化和假设基础上建立物理模型,钢渣罐的导热过程满足二维导热方程:
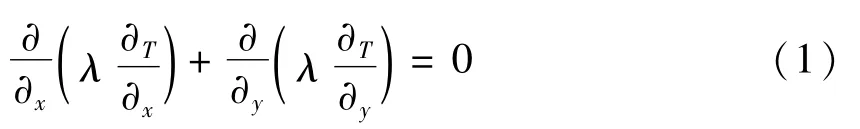
式中: x,y—计算点的位置;
T—温度,℃;
λ—钢渣罐罐壁的导热系数,与罐壁的材料有关,W/m·℃。
对于简化后的钢渣罐模型,其传热现象可以归纳为热对流与热辐射。因此建立的钢渣罐传热系统需满足以下边界条件:

边界既存在对流换热又存在辐射换热:
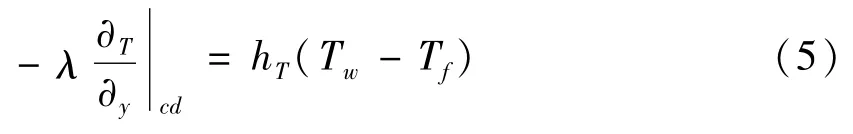
钢渣罐的外表面复合换热量Φ是由对流换热量和辐射换热量组成,转化公式如下:
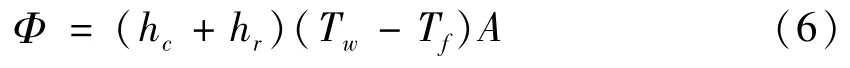
式中: hT—钢渣罐外表面的复合的传热系数,W/(m2·℃);
hc—对流换热系数,W/(m2·℃);
hr—辐射换热系数,W/(m2·℃);
Tw—钢渣罐的外表面温度,℃;
Tf—周围环境拥有的温度,℃;
A—物体表面面积,m2。
2.3 正问题求解结果
根据有限元方法进行正问题求解,图2为钢渣罐的温度场分布状况。由图2可得,钢渣罐内壁温度较高,钢渣罐壁温度随着离钢渣距离增加有所下降,整个钢渣罐温度分布以罐体中部为圆心,呈环形分布,在耳轴附近温度下降明显。
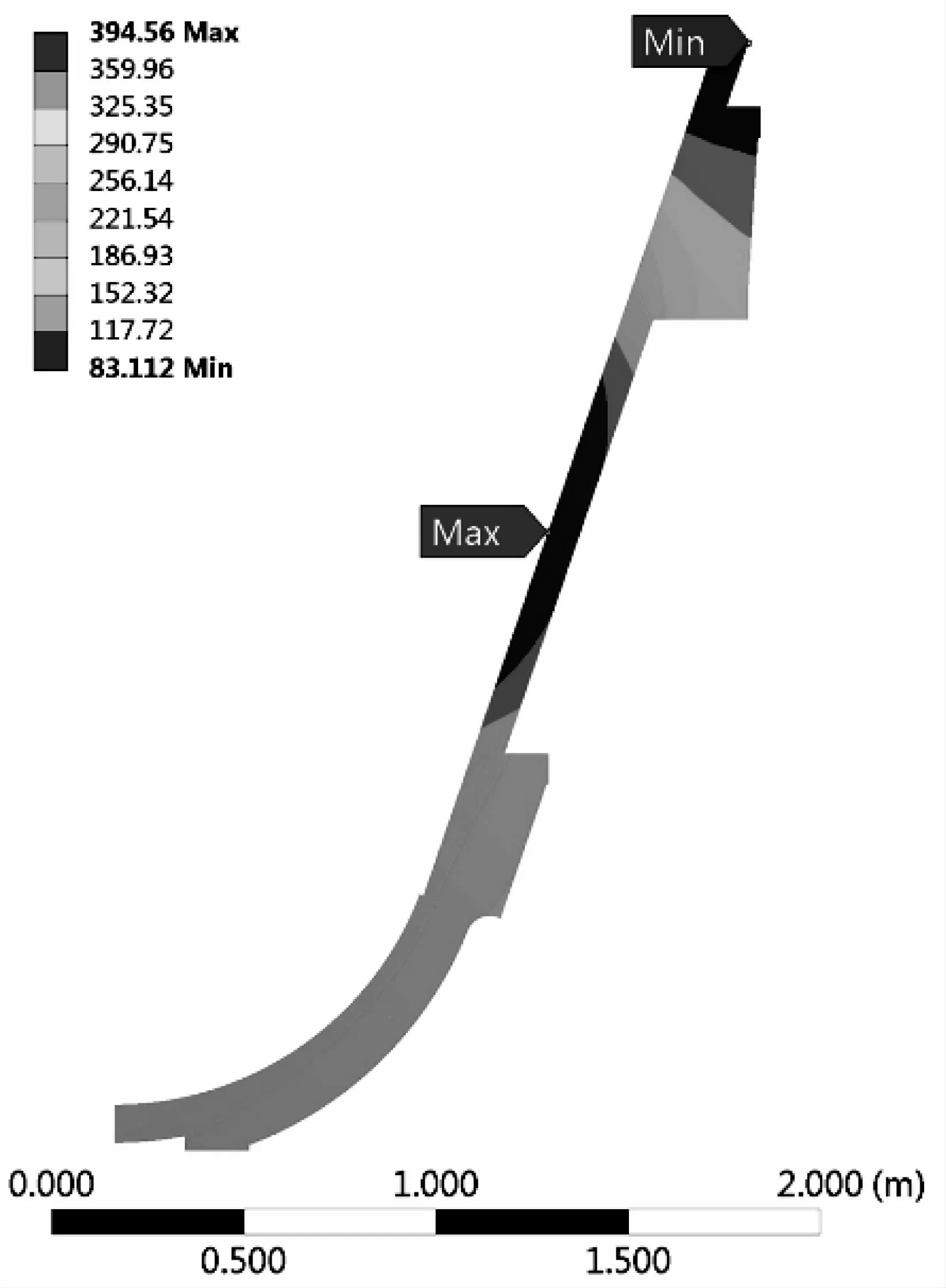
图2 温度分布云图
图3为钢渣罐外表面温度分布曲线图,能够直观看出罐体外表面的温度散布状况。由图3可知,最大温度在罐体中部,即腰线附近。罐体的最低温度出现在耳轴处,这是由于耳轴远离钢渣,有加强筋板辅助散热。
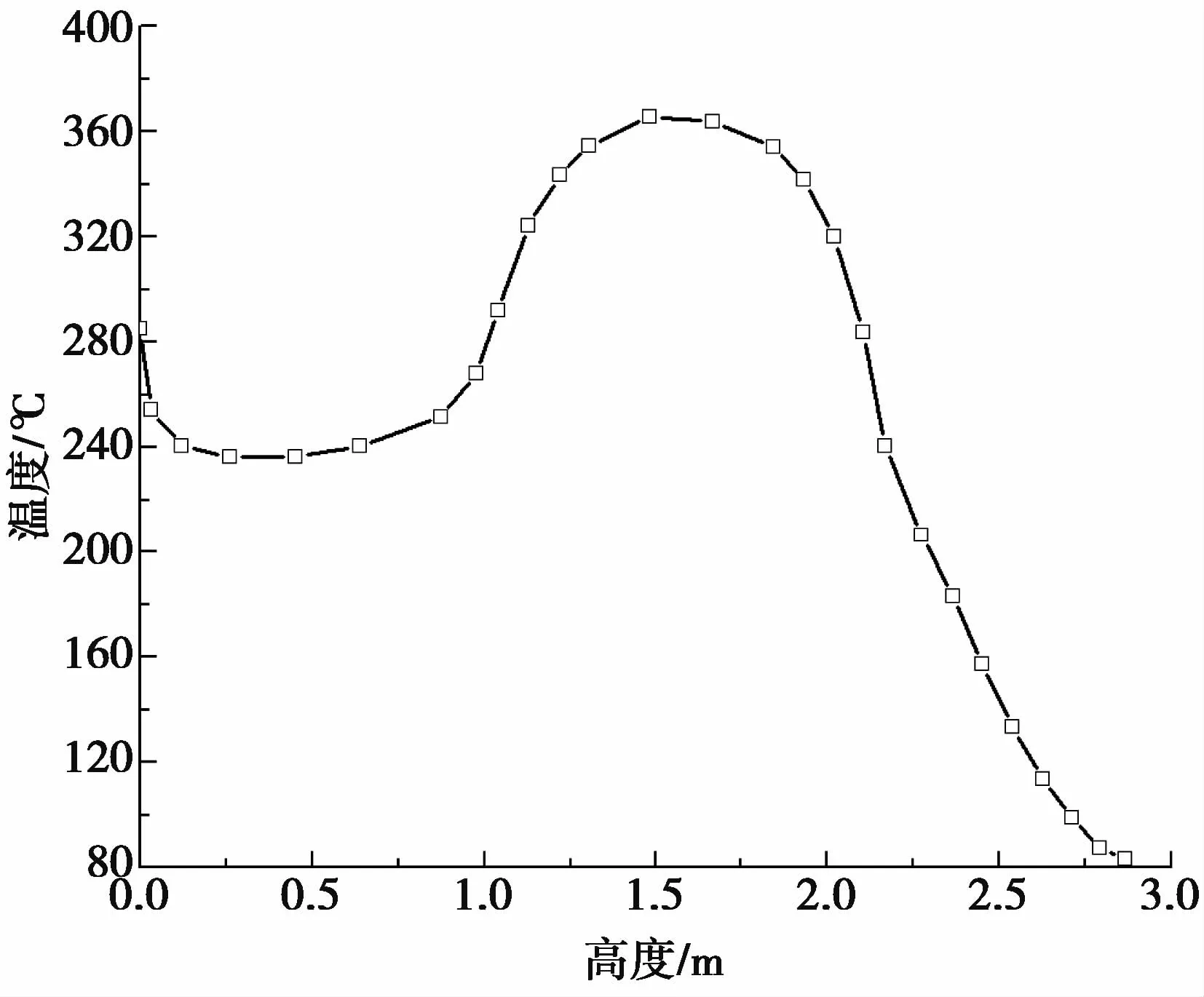
图3 钢渣罐外表面温度分布曲线图
3 反问题
由于钢渣罐的服役工况条件极其恶劣,且钢渣罐内钢渣为多种矿物的固溶体(属于硅酸盐类),直接获取钢渣的温度分布非常困难,但是可以较容易的获得钢渣罐外壁的温度信息。因此利用钢渣罐外壁一定数量的测点的温度信息,反演钢渣罐内钢渣的温度散布状况具有可行性。
3.1 反演的目标函数
根据已知钢渣罐热物理数据和边界条件,在钢渣罐外壁安放一定数量的温度测点,通过温度测点反馈信息来预测钢渣罐内壁的边界条件状况。假定设置了K个温度测点,测点处的温度值为Tmi(i=1,2,…,K),可以通过以下目标函数的最小值来解决该传热学反问题:
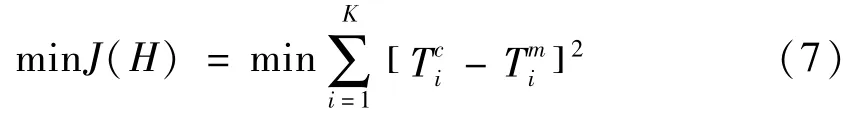
式中: H—待反演的温度值,℃;
3.2 钢渣温度分布反演
基于共轭梯度法,需要反演的温度值H要满足公式:

式中: Hn—需要进行反演的温度值,℃;
H—第n次猜想值,℃;
αn—迭代步长;
dn—共轭梯度的搜寻方向。
dn由式(9)确定:
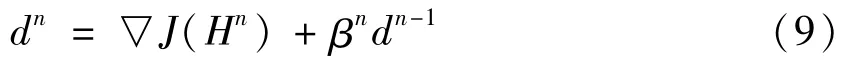
式中: βn—共轭系数;
▽J(Hn)—对象函数的梯度。
βn可由式(10)确定,▽J(Hn)可由式(11)确定:
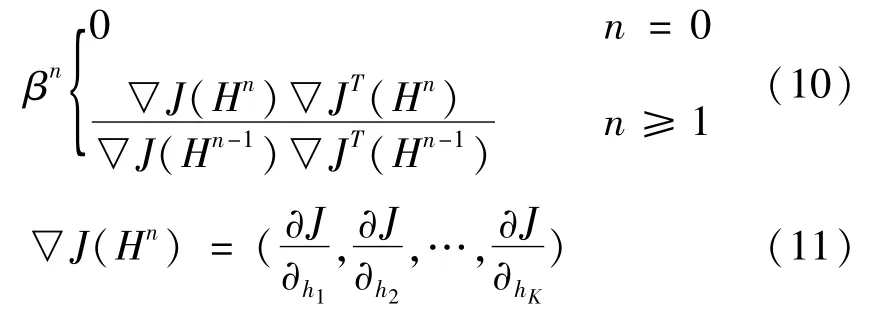
其中,

经过优化目标函数J(Hn-αndn)来确定搜索步长αn:
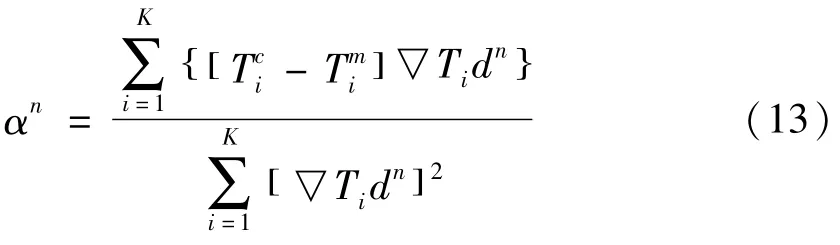
式中: ▽Ti—行向量,求解如下:
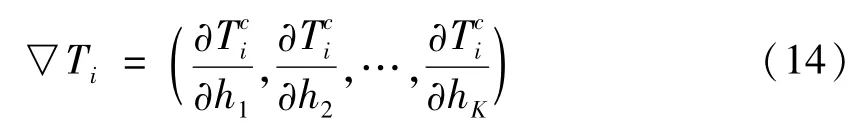
运用中心差分法来大致代替计算行向量▽Ti。
3.3 反演的收敛判断
运用共轭梯度法反推钢渣的温度散布时,假如符合式(8),那么就迭代中止,Hn是最终需要导出的反演结果。迭代时,目标函数的收敛判别是:
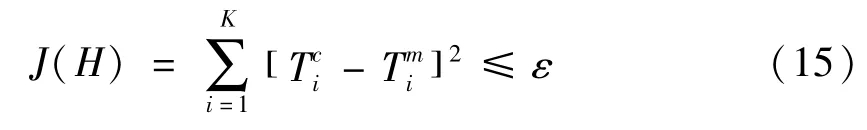
式中: ε—迭代终止阀值。
在现实生活中温度测量值Tmi肯定会有一定的测量误差,所以在数值模拟试验时,温度的实测值应基于真实值Tei增添一个任意测量误差,则温度的测量值应为:

式中: σ—标准状况下的测量偏差;
ω—服从标准正态分布的一系列波动数,其取值范围是[-2,2],且其平均值为0。
此时,迭代终止阀值为:

当存在测量误差时,目标函数的收敛条件为:

3.4 反演的基本流程
采用共轭梯度法反钢渣罐内钢渣温度分布情况的程序计算流程如图4所示:

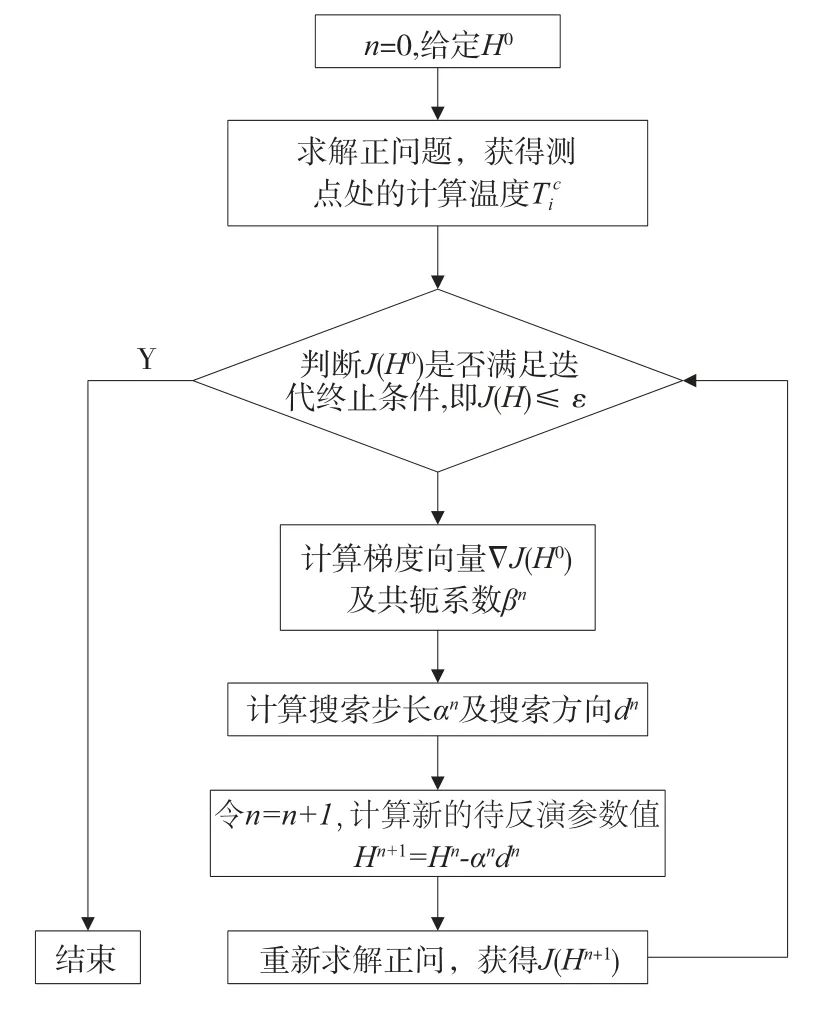
图4 反演流程图
4 仿真试验与结果分析
4.1 仿真实验条件
以真实传热边界参数数值求解导热微分方程得到钢渣温度场分布,以此来当作实际生产中的温度场分布,y是钢渣罐的深度,即待反演的钢渣温度实际分布情况为抛物线:
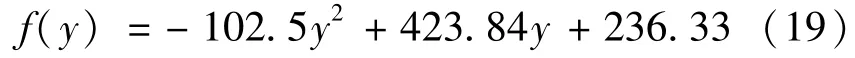
结合正问题的求解结果,使用正问题计算所得的钢渣罐外壁温度,模拟钢渣罐外壁测量温度值,以测量值为基础上填加一个未定的测量差作为反问题的输入参数。为评价反演结果精度与可靠性,定义待反演点处温度值的可接受的误差为:
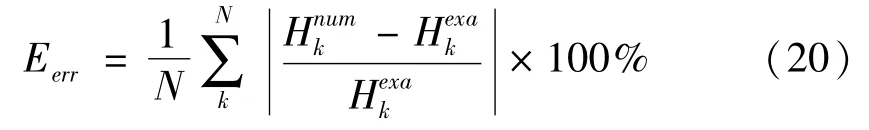
N—需要反演点的数目。
初始温度H0=1400℃,环境温度Tf=20℃。取外壁温度的测点数k=14,测点从钢渣罐的底端到罐口依次均匀分布在外壁上,给定测量误差σ=1.0℃,迭代终止阀ε=3。采用共轭梯度法对符合工程实际应用下的渣罐内的钢渣温度分布情况进行反演,图5为反演得到钢渣温度分布情况所示,表1为误差分析结果。
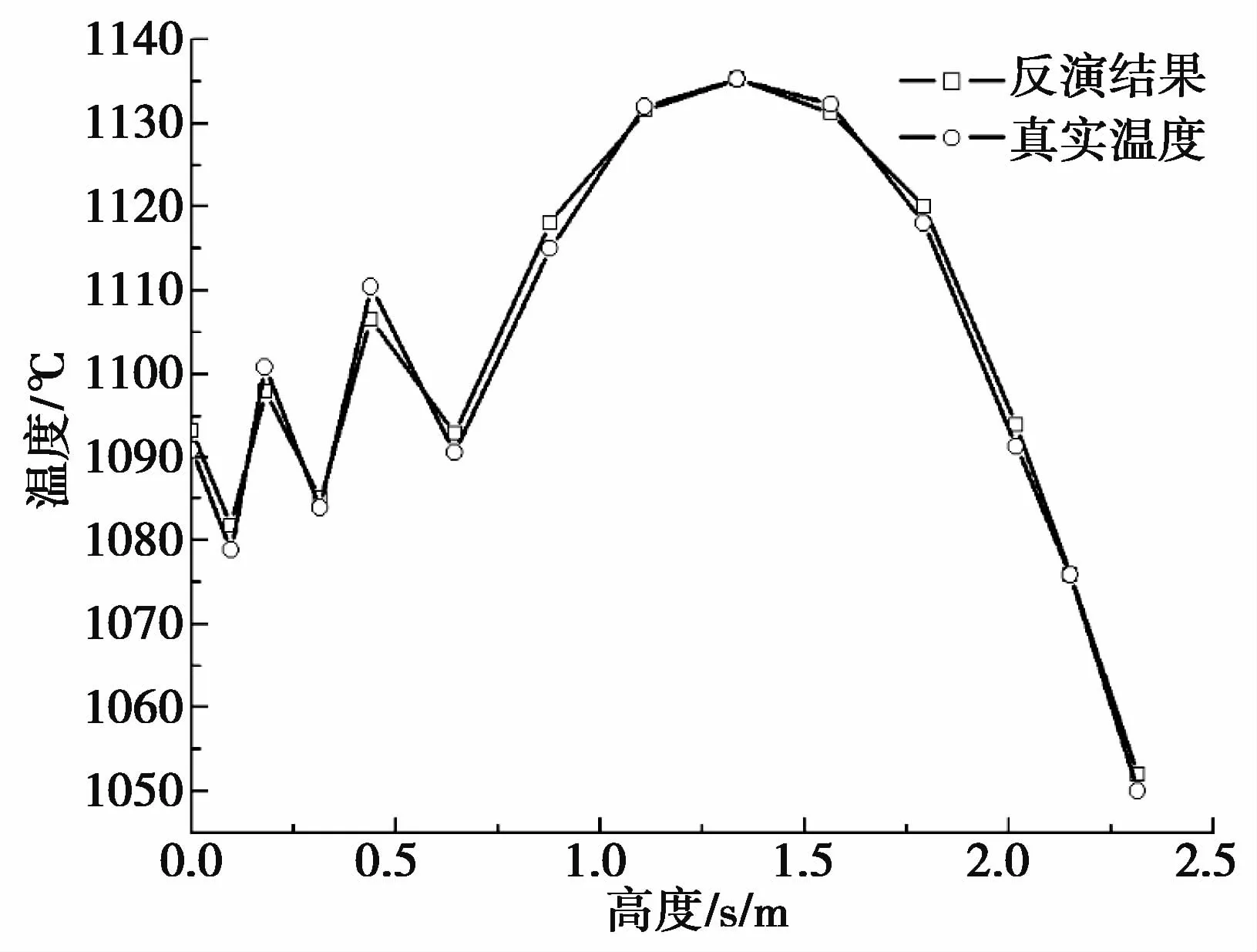
图5 CGM反演结果

表1 误差分析
从以上反演结果中能够看出,获取的数值略偏离于真实值,因为不适定是反问题自身的特点,在求解的过程中输入参数是欠正定或超正定的,因此偏差是无法避免的。结合图表中可以得出,算例结果的最大误差是0.16%,相应的最大误差值是5℃,误差值非常小,因此本文所运用的共轭梯度法能够完成对钢渣温度散布状况的反演,且具有较高的精度。
4.2 初始值的影响
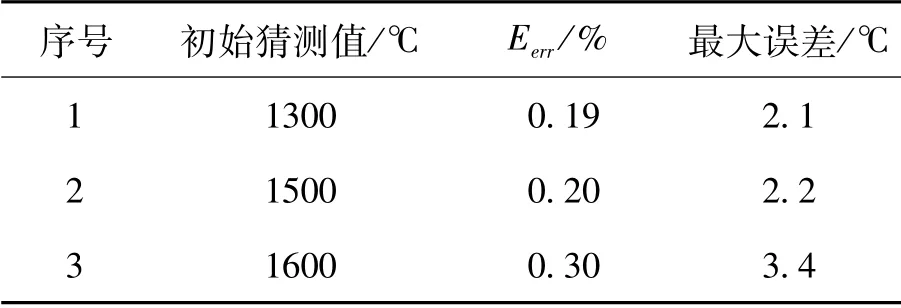
表2 误差分析
由上述不同的温度猜想值得到的钢渣温度散布的反演结果的平均相对误差依次是0.19%、0.20%、0.30%,对应的最大反演误差分别为2.1℃、2.2℃、4.7℃。从图6中可以看出,当温度分布的初始值比较接近真实值时,CGM反演模型能够取得较优异反演结果。在初始猜想值出现明显偏离真实值的状况下,反演结果的误差随之增大,所以初始猜想值会干扰反演状况。
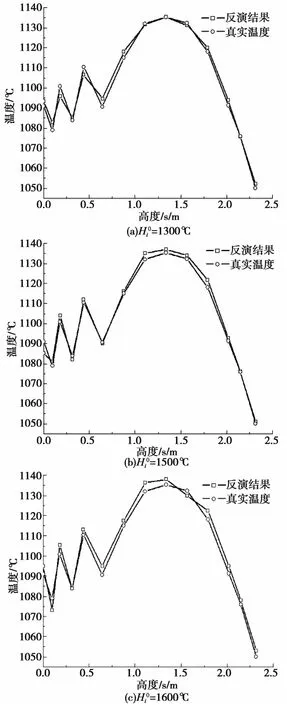
图6 反演结果
4.3 测点数目的影响
取初始温度猜测值H0=1400℃,测量误差σ=0℃,分别对温度测点数目K=14、K=11、K=8这三种方式进行反演,温度测点均匀分布在钢渣罐的外壁上。
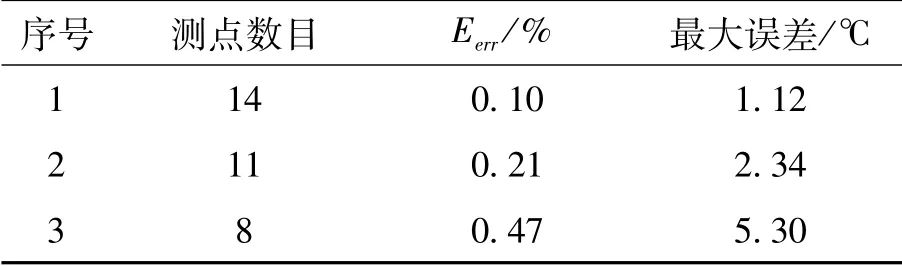
表3 误差分析
测点数目分别为8、11和14时,由CGM得到的钢渣温度散布状况,其平均相对误差分别为0.10%、0.21%、0.47%,对应的最大误差分别为1.12℃、2.34℃、5.30℃。结合图7可以得出,测点数目K=11时便能够得到较为理想的反演结果,反演结果的平均相对误差因为测点数目增加而减小,其原因是温度测点数目的提升,能获得的已知信息增多,相应的温度信息也就更加完整,所以反演精度会有所提高,即测点数目的增加有益于反演精度。但是较多的测点数目将会增加计算量,会增加计算负担,所以结合实际工程应用,应尽量减少测点数目。
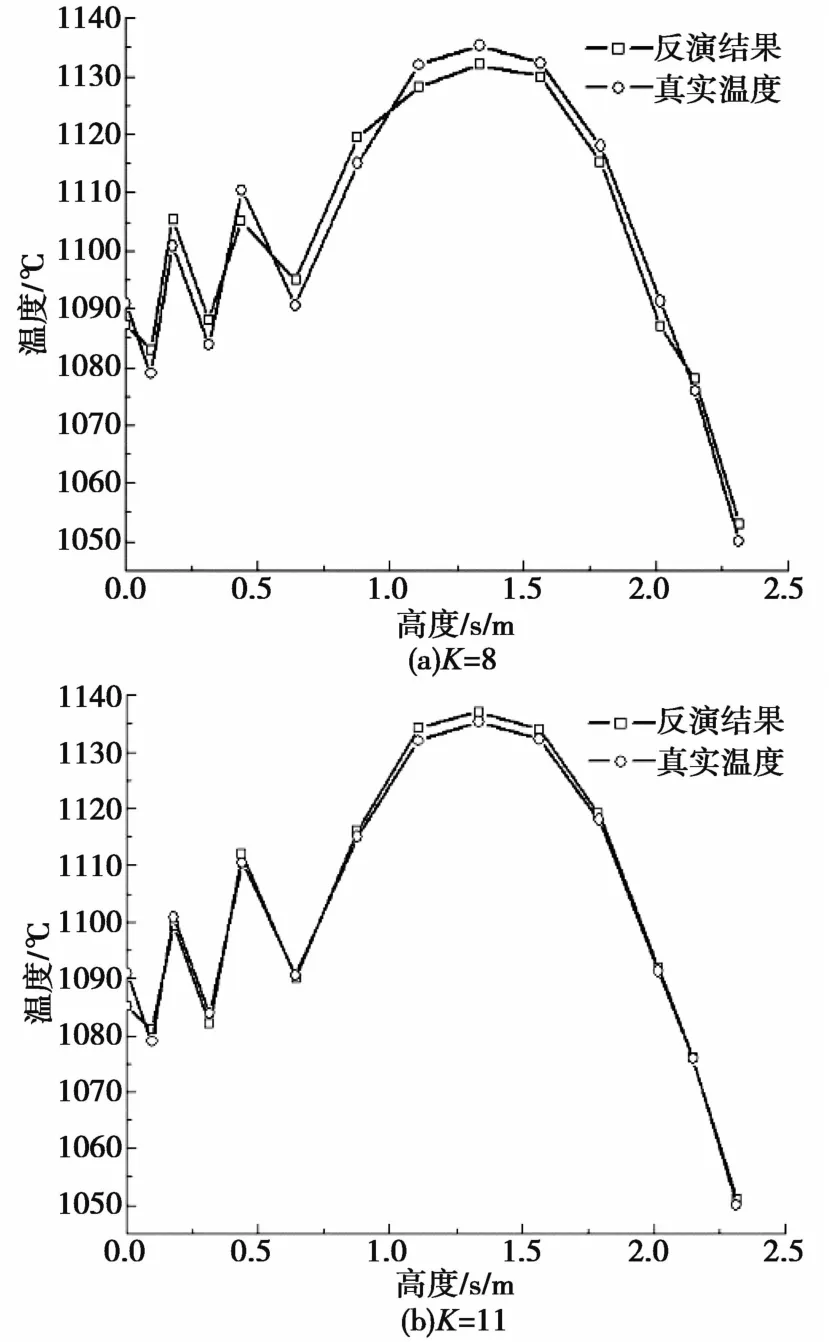
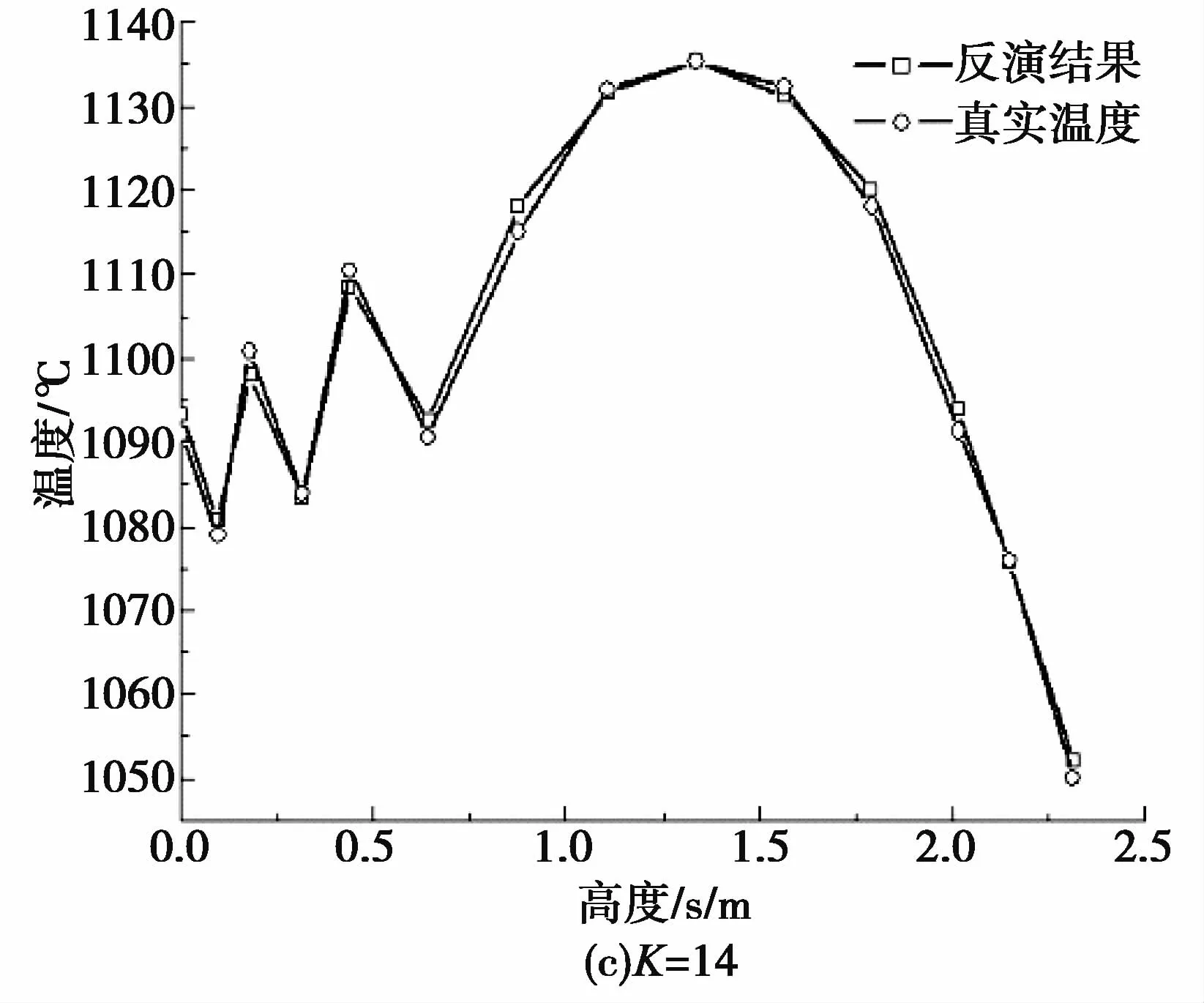
图7 反演结果
4.4 测量误差
反问题的不适定性导致反演结果略微敏感于测量误差,即测量温度值的极小偏差,便有可能导致结果出现波动。
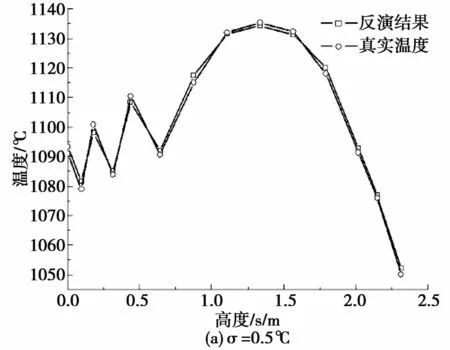
对测量误差的抗干扰性是判断反演算法有效性的标准之一,取温度初始猜测值H0=1400℃,K=14,温度的测点位置保持不变,以此来判别测量误差对CGM反演效果的干扰程度大小。取测量标准差分别为σ=0.5℃、σ=1.0℃、σ=1.5℃,按照公式(17)设定终止阀值。从表4可以看出,各个误差值下结果平均相对误差依次是0.13%、0.25%、0.37%,最大误差值依次是1.42℃、2.81℃、4.70℃。结合图8可以看出,测量误差较小时,采用共轭梯度法(CGM)可以得到较准确的反演温度,测量标准差σ的增大会使温度反演误差增大。
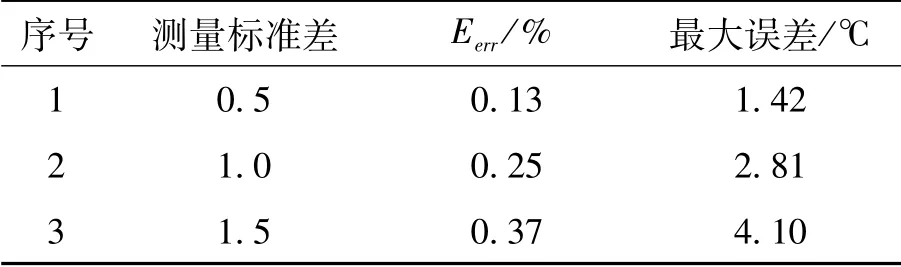
表4 误差分析
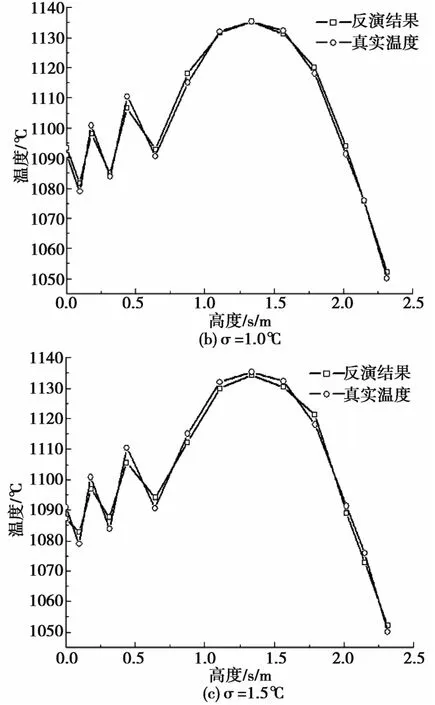
图8 反演结果
4.5 测点位置的影响
钢渣温度在该处的灵敏度大小与测点位置有关系,通常情况下,测点处的温度灵敏度与测点到待反演点的距离有关。灵敏度的大小决定了反演结果的好坏,因此有必要分析测点位置对所得结果的干扰程度。令温度初始猜想值H0=1400℃,测量误差σ=0℃,使用以下布置方式。
方式一,所有测点依次散布在钢渣罐的罐体表面。方式二,部分测点分布在钢渣罐外表面与加强筋外表面之间。方式三,部分测点分布在加强筋外表面。上述3种测点布置方式得到的钢渣温度分布的平均相对误差如表5所示。
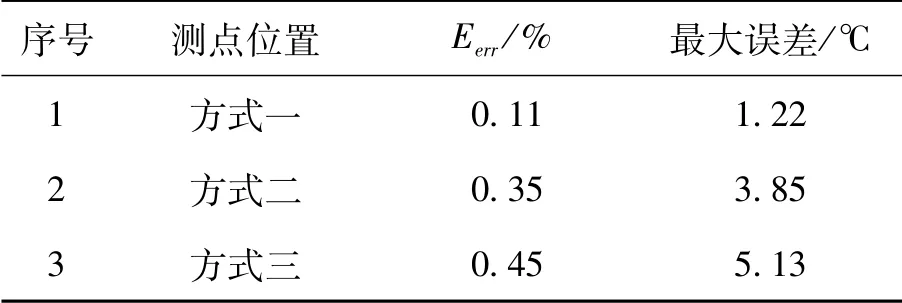
表5 误差分析
分别为0.11%、0.35%、0.45%,对应的最大误差分别为1.22℃、3.85℃、5.13℃。从图9中可以得出,测点位置所产生的影响明显,温度反演结果随着测点位置远离待反演点位置而变差。此现象在罐底附近及罐口附近较为明显,主要原因是罐底附近加强筋很多,罐体温度差别较大;罐口不与钢渣直接接触,可以利用的有效测点信息较小。所以利用方式一和方式二的测点布置获得的反演效果不太理想。
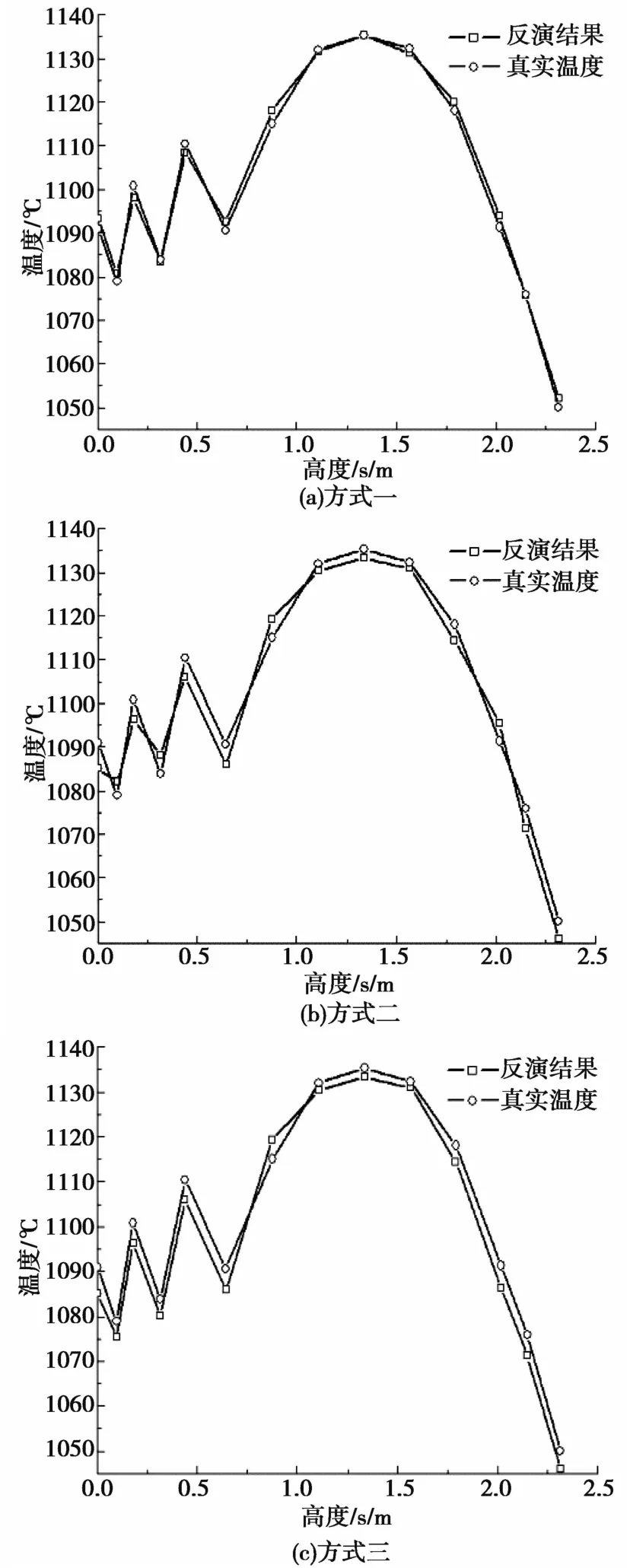
图9 反演结果
5 结论
本文在12m3钢渣罐传热系统模型的基础上,利用共轭梯度法以渣罐内钢渣温度分布为反演量进行仿真试验,证实了共轭梯度法的实用性,且探究了四种因素对反演精度的影响,主要结论如下:
(1)初始猜测值越偏离于真实值,反演精度就越差。基于3个不一样的初始猜想值,本文所运用的反演模型依然能够获得优异的反演数据。
(2)较少的测点数目会致使反演精度比较差,即反演精度随着测点数目的增多而有所提高。布置适当的测点数目,运用共轭梯度法能够获精度比较高的反演数据结果,本文采用14个测点数目即可获得较高精度。
(3)测量标准差σ在相对的测量误差范围内对反演精度影响较小,但当误差进一步增大时,反演精度随之降低。当σ≤1.0℃时,共轭梯度法能获得符合实际的反演结果。
(4)测点位置对反演精度的干扰比较显著,反演结果因测点位置的不同而表现出较大差异。本文所采用的较差测点布置方式一和方式二得到的反演结果不太理想,即测点位置需能够反映待反演参数。
