压力容器自动排气阀工作性能分析及优化

2022-06-09张建明2李道朋

液压与气动 2022年3期

杨运，张建明2，李道朋，傅波

(1.四川大学机械工程学院，四川成都 610065； 2.中国工程物理研究院化工材料研究所，四川绵阳 621900)

引言

排气阀作为承压容器中的一个重要部件，其性能好坏直接影响着整体的使用效果[1]：例如，在暖通系统和供水系统中，依靠排气阀来排除系统内多余的空气，保证系统稳定正常的工作；在一些高压成型设备中，需要将工件模具放入盛满液体的密闭容器中，通过液体传压成型，这也需要排气阀来控制密闭容器的充排气[2]。传统的手动排气装置主要在工作缸的最高处外接高压截止阀。容器的最大工作压力受限于截止阀的工作压力，且需要人员在高压环境中近距离观察排气口状况来手动关闭截止阀，危险性高，对截止阀的可靠性要求较高[3]。自动排气装置则基于气动或电动执行机构进行阀门远程控制，其组成机构体积较大，需要专门电气系统控制；排气阀门出口带1个转存油箱，气体是否排尽由油箱内的液位传感器来判断，因油滴粘滞，传感器也容易造成误判断[4]。

针对有风险的手动排气装置和复杂的自动阀门，本研究介绍了一种结构简单，不需要单独控制的新型自动排气阀[5]，对其进行了理论分析计算和流场仿真，获得了阀体内的流动情况、流阻分布及受力情况；分析比较了不同参数对浮子动作的影响；针对阀内流阻分布不均的现象，进行了结构优化，使浮子在满足对其动作要求的同时，有着更好的工作稳定性。

1 自动排气阀的结构与工作原理

如图1所示为自动排气阀结构图，其主要由C形卡环、阀座、浮子、密封环和O形圈等组成。浮子通过下端的C形卡环Ⅰ来限制其上下运动的位移，浮子下端开有贯穿于壁面的半圆形裙孔。密封环放置于浮子上端开设的阶梯槽内，与O形圈一起实现排气口的开闭。在C形卡环Ⅱ的限制下，其在阶梯槽内也可进行一小段上下位移。其中，为防止O形圈被高速气流吹出，将其所在槽孔设为上窄下宽的梯形[6-7]。

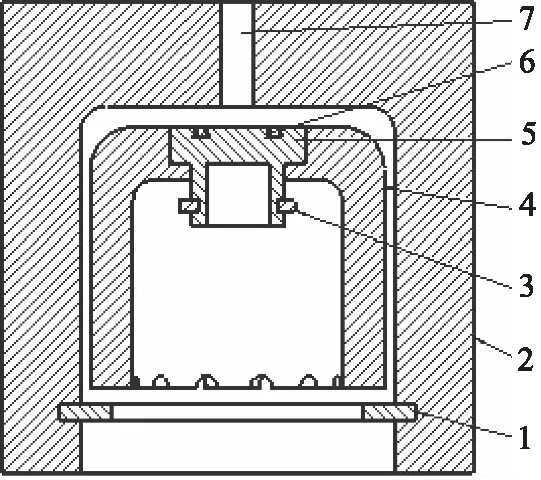
1.C形卡环Ⅰ 2.阀座 3.C形卡环Ⅱ 4.浮子5.密封环 6.O形圈 7.排气口图1 自动排气阀结构Fig.1 Automatic exhaust valve structure

安装时，阀座竖直安装于压力容器顶部，在自身重力的作用下浮子和密封环组件自由下落，由阀座上的C形卡环Ⅰ限制在阀座内。如图2a所示，容器充液排气时，空气进入阀座，通过浮子下端的裙孔进入浮子和阀座的间隙处，最终流过浮子上端面，从排气口排出。因气体黏度小，产生的气阻小于浮子和密封环的重量，密封环端面无法与阀座顶面接触，未形成密封效果；如图2b所示，当工作液充满容器时，工作液开始进入阀座，浮子组件开始浸泡在液体内。由于液体黏度、密度等远大于气体，在其黏滞力和浮子等作用下，浮子和密封环组件向上运动直到密封环接触排气口，O形圈开始进行密封工作，防止工作液从排气口漏出。浮子在压力作用下与密封环分离，处于静压环境中，不承受结构力。随着内部容器压力不断上升，密封环在容器内的静压作用下紧紧的压在阀座上端面，密封效果也越来越好。

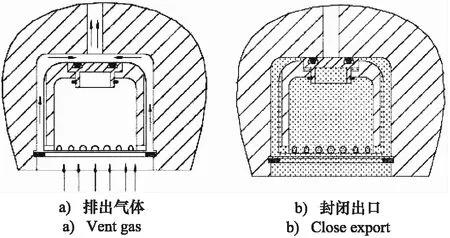
图2 工作效果Fig.2 Working renderings

2 自动排气阀的理论分析与流场仿真

对排气阀进行理论分析，如图3所示，排出空气时需要浮子不上浮，即取浮子刚离开C形卡环I时分析[8]，可得到一临界间隙值δ1；当工作油进入，这时需要浮子上浮直到封闭排气口，可得到一临界间隙值δ2，设计时浮子与阀座侧面间隙应在(δ1，δ2)之间。

图3 结构尺寸参数Fig.3 Structural dimension parameter

根据使用情况，工作温度为150 ℃，此时空气密度为ρ1=0.83 kg/m3，动力黏度为μ1=2.39×10-5Pa·s；设定工作介质为DY-300型号导热油，导热油运动黏度υ2=1.01×10-6m2/s，密度ρ2=916 kg/m3，动力黏度为μ2=9.252×10-4Pa·s。同时根据实际的应用场合和条件[9]，设置初始值如下：体积流量qv=20 L/min，阀座内径D=60 mm，高度H=50 mm，浮子高度h=43 mm，壁厚ε=5 mm，浮子中开设的阶梯槽厚为8 mm，浮子底部所开裙孔半径r=1.5 mm，数量n=24。

2.1 临界间隙δ1的计算

对浮子进行受力分析，所受主要力为间隙内空气对浮子的向上的黏性摩擦力F1、空气对浮子下端面及内腔顶部向下的压力F2、空气对浮子上表面向下的压力F3以及自身整体向下的重力G。如图4所示，为部分分析参数示意图，分别对每个分力进行分析计算[10-11]。

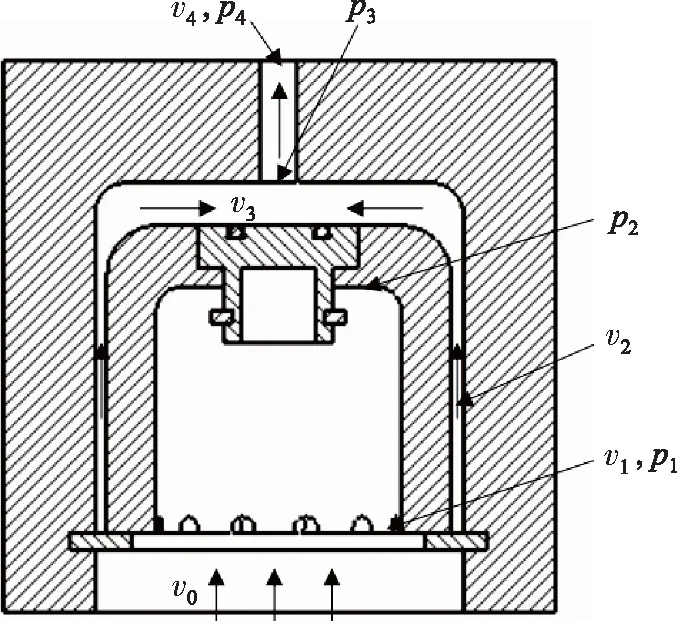
图4 分析参数示意图Fig.4 Analysis parameters

1) 自身重力G

其他参数已知时，浮子若仅在空气通过时就上浮，则δ1的值很小；忽略相对质量很小的O形圈和C形卡环Ⅱ，则浮子质量可看作几乎不变(此时d1≈D)。结合其他参数，构建出三维模型。浮子材料选为聚四氟乙烯，密度为2200 kg/m3；密封环材料为30CrMnSiA，密度为7850 kg/m3，测得其体积V浮为41152.354 mm3，V密为3338.918 mm3，则所求重力为：

G=(ρ浮V浮+ρ密V密)·g=1.145 N

(1)

式中，G—— 浮子整体重力，N

ρ浮，ρ密—— 浮子、密封环密度，kg/m3

V浮，V密—— 浮子、密封环体积，mm3

2) 黏性摩擦力F1

空气从间隙通过，向排出口流通时，对浮子外壁面会产生一个向上的摩擦力。对于同心圆柱环形缝隙，在δ/d1<<1的情况下，可以将环形间隙流动近似看成平行平板缝隙中的流动，此时缝隙的宽度B=πd1。将空气在浮子与阀座间隙内的流动近似为牛顿流体的层流流动，根据牛顿内摩擦定律，有：

(2)

A=πd1h

(3)

式中，F1—— 间隙内空气与浮子接触面上的内摩擦力，N

A—— 间隙内空气与浮子的接触面积，mm2

dv/dz—— 速度梯度，1/s

μ1—— 空气的动力黏度，Pa·s

d1—— 浮子外径，mm

h—— 浮子高度，mm

根据平行平板缝隙间层流运动的常微分方程式得：

(4)

式中，Δp—— 压力损失，MPa

通过间隙的流量qv：

(5)

式中，B—— 缝隙的宽度，mm

δ—— 间隙大小，mm

v—— 速度，m/s

利用平行平板缝隙间的层流规律，代入边界条件：z=0，v=0；z=δ，v=0，可求得压强损失Δp。z=0时的速度梯度dv/dz，代入式(2)可求得：F1=24μ1hqv/(D-d1)2。

3) 空气对浮子下端面及内腔顶部的压力F2

如图5所示，选取空气流入浮子内部处的截面作为缓变过流断面0-0，空气排出口处截面作为缓变过流断面4-4，并以过流断面0-0所在的平面为基准面，根据实际流体总流的伯努利方程得：

(6)

式中，z0，z4—— 断流面0-0，4-4相对位置高度，mm

p0，p4—— 断流面0-0，4-4压力，MPa

v0，v4—— 断流面0-0，4-4平均速度，m/s

α0，α4—— 断流面0-0，4-4动能修正系数

ρ1—— 空气密度，kg/m3

hf—— 能量损失

不考虑能量损失hf，联立流体的连续性方程：

qv=A0v0=A4v4

(7)

式中，A0，A4—— 圆截面0-0，4-4的面积，mm2

图5 分析示意图(介质为空气)Fig.5 Analysis schematic diagram (medium is air)

代入已知条件α0=α4=1，z0=0 mm，z4=70 mm，p4=0 MPa(表压力)，可求得浮子下端面压力p0为：

(8)

式中，ρ1—— 空气密度，kg/m3

z4—— 断流面4-4相对高度，mm

qv—— 间隙的流量，L/min

d2—— 浮子内径，mm

d4—— 排气口直径，mm

不考虑由于空气所受重力在竖直方向引起的压力差，则所求F2近似为：

(9)

4) 空气对浮子上表面压力F3

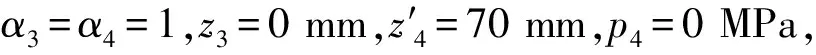
在距离中轴线任意半径为r处取一小段dr的流层，近似可把这薄流层视为宽度为2πr的平行平板间的流动，由流体力学的知识可知，浮子上表面沿径向的压力梯度为：

(10)

式中，σ—— 浮子上表面与阀座间隙值，mm

μ1—— 空气的动力黏度，Pa·s

利用边界条件：r=d4/2时，p=p3，可求得浮子上表面的压力分布。对微元面积2πrdr积分，简化可求得空气对浮子上表面总作用力F3为：

(11)

式中，d1—— 浮子外径，mm

d4—— 排气口直径，mm

p3—— 断流面3-3的压力，MPa

qv—— 间隙的流量，L/min

根据浮子刚好浮起的临界状态，满足方程式：

F1+F2=F3+G

(12)

将各个分力的表达式代入上式，可求得浮子外径d1=59.923 mm，则间隙δ1=0.039 mm。

2.2 临界间隙δ2的计算

当容器内的空气排尽时，油液慢慢进入阀内，油液面会逐渐上升，如图6所示，选择一特殊位置2-2(即油液面刚好上升到浮子内腔顶部)进行分析，假设此时浮子被油液抬起，计算此时临界间隙。

图6 分析示意图(介质为空气和油)Fig.6 Analysis schematic diagram (medium: air and oil)

此时浮子受到间隙内导热油对浮子表面的黏性摩擦力F1、油对浮子下端面及内腔顶部的压力F2、空气对浮子上表面的压力F3、自身重力G。

1) 浮子与密封环所受重力G

经分析，此时侧面间隙比空气流过时(即δ1)要大得多，不再忽略间隙对浮子重量的影响(不再将d1视为D计算)，由之前计算可知初始重力值为1.145 N，当浮子外径变化时，浮子体积变化近似为：

(13)

2) 黏性摩擦力F1

油通过浮子下端裙孔，缓慢进入间隙内，当完全淹没裙孔时，浮子内腔空气还可以从密封环所在的阶梯槽缝隙排出，如图6所示，选取油面上浮到浮子内腔顶部这一特殊位置(2-2平面)分析，计算过程和前面排出空气时类似，可得：

(14)

式中，μ2—— 热导油的动力黏度，Pa·s

D—— 阀座内径，mm

d1—— 浮子外径，mm

h—— 浮子高度，mm

3) 油对浮子下端面及内腔顶部压力F2

(15)

式中，p2—— 环形截面2-2的压力，MPa

ρ1—— 空气密度，kg/m3

qv—— 间隙的流量，L/min

D—— 阀座内径，mm

d1—— 浮子外径，mm

选取空气流入浮子与阀座间隙处的截面作为缓变过流断面1-1，以1-1所在平面为基准面，对面1-1，2-2分析，其中1-1的截面A1为：

(16)

式中，n—— 浮子底部裙孔的数量

r—— 浮子底部裙孔的半径，mm

(17)

式中，p1—— 断流面1-1的压力，MPa

p2—— 断流面2-2的压力，MPa

ρ2—— 导热油密度，kg/m3

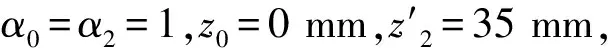
(18)

考虑到由于导热油所受重力在竖直方向引起的压力差，浮子内腔顶部压力p5近似为：

p5=p0-ρ2gh′

(19)

油对浮子下端作用面积S1，内腔顶部作用面积S2近似为：

S1=n·2rε

(20)

式中，n—— 浮子底部裙孔的数量

r—— 浮子底部裙孔的半径，mm

ε—— 浮子壁厚，mm

(21)

可求得：

4) 空气对浮子上表面压力F3

分析计算过程与前面相似，可求得：

根据临界状态，此时满足平衡方程式(11)，将各个分力的表达式代入，可求得浮子外径d1=58.090 mm，则间隙δ2=0.955 mm。

2.3 参数对临界间隙的影响

综上，由已知数据，求得浮子与阀座的间隙设计范围应为0.039～0.955 mm。当改变一些如入口流量qv、浮子高度h、壁厚ε和阀座内径D等参数时，均会对临界间隙产生一定的影响。

1) 入口流量qv对临界间隙的影响

将用方程式(12)分别代入5个不同的入口流量qv，计算出其对应的临界间隙，如图7所示。由图7可知，当入口流量增大时，临界间隙δ1，δ2也在增大。

图7 流量与临界间隙Fig.7 Flow and critical clearance

2) 浮子高度h对临界间隙的影响

浮子高度的变化会改变浮子所受重力G，同时浮子外壁面的面积的变化将改变F1，而F2和F3的变化接近于0。选取5个不同高度值h，将变化的数值重新代入之前对应的公式中求解，计算出相应的临界间隙。如图8a、图8b所示，为高度对两种间隙的影响。随着浮子高度h逐渐增大，临界间隙呈缓慢增大趋势。

图8 浮子高度与临界间隙Fig.8 Float height and critical clearance

3) 浮子壁厚ε对临界间隙的影响

浮子壁厚的变化会改变浮子的质量G，同时下端面及内腔顶部面积会发生变化，F2发生改变。浮子壁厚变化后的浮子体积变化量为：

(24)

浮子下端面及内腔顶部受到油的压力为：

(25)

将变化的参数代入平衡方程，求出不同壁厚时的临界间隙，如图9所示，随着浮子壁厚ε增大，δ2逐渐减小，δ1也在减小但是变化非常小，可看做几乎没有影响。

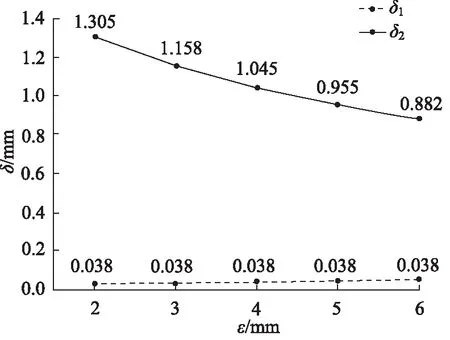
图9 浮子壁厚与临界间隙Fig.9 Float wall thickness and critical clearance

4) 阀座内径D对临界间隙的影响

选取5个不同的阀座内径D，分别计算出其对应临界间隙。如图10a、图10b所示，为不同内径D和间隙的关系。D∈(40,60) 时，当D增大，δ1几乎无变化，δ2先减小后增大。

2.4 流场分析

1) 排出空气时的流场分析

流场仿真分析基于Fluent软件进行[12-14]，这里主要关注浮子能否稳定完成排气功能，即在排气时不上浮，保证排气口的通畅。为减少计算量，对轴对称结构的排气阀采用半模型的建模仿真。模型由两部分组成，外部为流体，内部为固体(浮子与密封环构建成整体)，考虑浮子底部卡环对流体流动的影响，流体部分的底部增加一个缩颈结构。在Fluent中进行流体分析时，只需保留流体部分，故在前面处理中利用布尔减运算将浮子部分剖除，对模型结构进行分组命名，如图11所示。

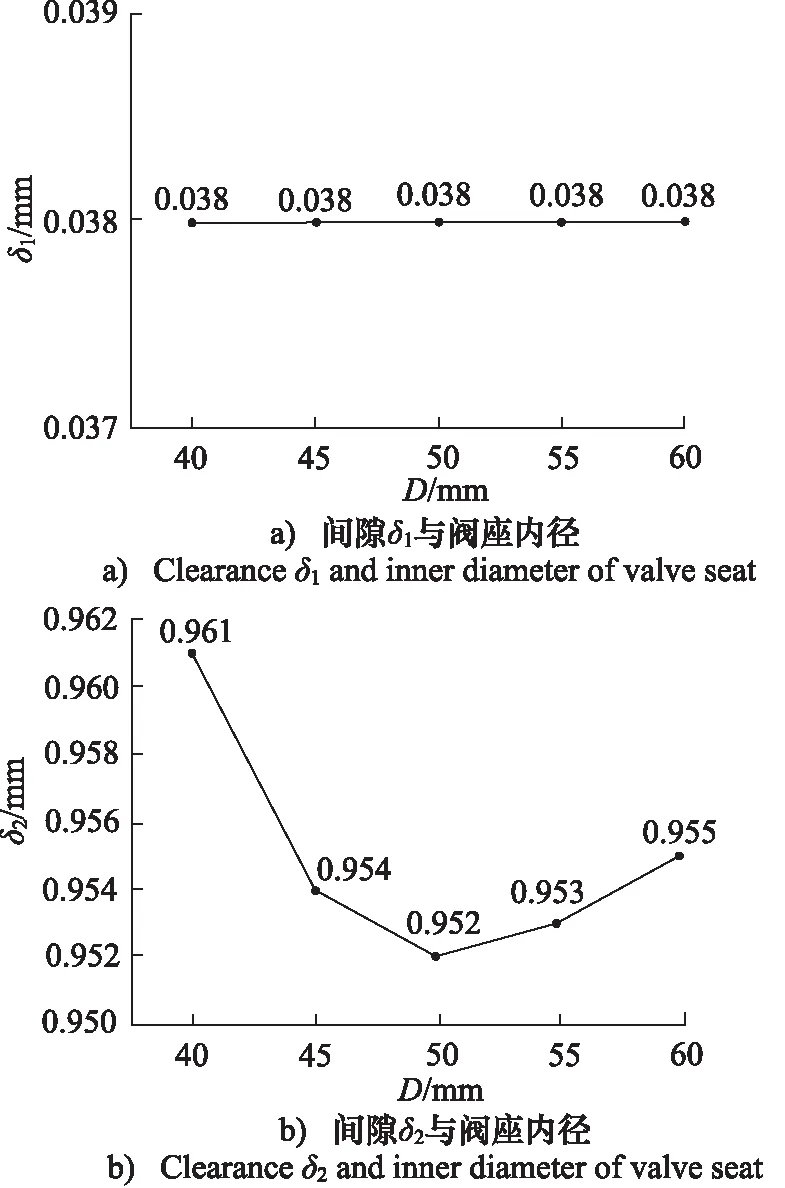
图10 阀座内径与临界间隙Fig.10 Valve seat bore and critical clearance

图11 空气流场仿真模型Fig.11 Simulation model of air flow field

此为单相流模型，将模型划分网格后在Fluent中进行仿真计算，可以获取空气排出稳态下流场的各种信息，如图12所示，为d1=59.2 mm下的压力云图。由图可知，浮子腔内压力较高，在间隙内，流体黏性的存在使其向上流动时压力逐渐降低，一直到出口处压力减少至零值，与实际情况相符。

通过调取后处理的数据获得浮子所受竖直向上的总合力为0.492 N，小于浮子自身重力，浮子不会向上运动，能满足使用的需求。

图12 d1=59.2 mm时流场压力云图Fig.12 Flow field pressure cloud diagram(d1=59.2 mm)

2) 封闭排气口时的流场分析

此时为压力容器的主要工作状态，主要分析油液进入一定位置时，浮子能否向上运动封闭排出口，并查看阀内的压力和速度等情况。模型以油和空气的分界面为界限分割为两部分，上下两实体分别赋以空气和油液两种材料，如图13所示，为其流场仿真模型。

图13 气-油混合流场模型Fig.13 Gas-oil mixed flow field model

此时分析模型为多相流瞬态分析。将导入的模型划分网格后在Fluent中进行仿真计算，可得到阀体内流场压力、速度及剪切力等分布云图。如图14所示，为流场压力云图。其压力变化趋势与气体的仿真结果保持一致：浮子腔内保持最高压力，在间隙流动过程中出现了压力迅速减小的现象。取不同浮子外径d1进行分析，不同的浮子直径对腔内压力值有很大的影响，随着外径的增大最高压力升高十分显著。

如图15所示为d1=59.2 mm时的速度云图，其速度分布与之前排出空气时的流场规律基本相同：在浮子空腔内速度基本为零值，在浮子底部间隙入口处，浮子间隙以及顶部出口处有明显的速度分层现象。

如图16所示为d1=59.2 mm时的流场剪切力云图。剪切应力主要分布在浮子间隙壁面上，这是因为油液具有较高的黏性，而在顶端出口处，虽然空气在此处依然有较大的速度梯度，但是空气的黏性很小，所以此处的剪切应力值相对很小。

同样调取后处理的数据获得浮子在竖直向上的方向上的合力值，求得在d1=59.2 mm时，竖直向上的合力为92.697 N，大于自身重力，浮子能向上运动封闭排气口，满足使用要求。

图14 流场压力云图Fig.14 Flow field pressure cloud diagram

图15 d1=59.2 mm时流场速度云图Fig.15 Flow field velocity cloud diagram (d1=59.2 mm)

图16 d1=59.2 mm时流场剪切力云图Fig.16 Flow field shear force nephogram(d1=59.2 mm)

3 自动排气阀结构优化

针对上述自动排气阀，由仿真结果可知，在排气阀工作的常态，即排气口封闭时，阀内压力、速度及剪切力等有着较大的差值变化，为改善其分布情况，增强浮子工作时的稳定性，现对结构进行优化：在原侧面裙孔的基础之上，开设半径为r，垂直于浮子底部，贯穿整个侧面的半圆柱形导流槽[15-16]，如图17所示。主要为了观察排气口闭合时阀内的情况，故只对油液进入阀内，浮子要上升时的临界状态进行分析，即求解新的δ2，并将新模型进行三维流场分析。

图17 改进浮子结构Fig.17 Improved float structure

3.1 优化后的理论分析

1) 浮子与密封环所受重力G

以浮子开槽半径r和数量n作为变量，初始预设的浮子与密封环所受重力为G0=1.145 N(此时r=1.5 mm，n=24)，当浮子开槽半径和数量变化时，浮子体积的变化量为：

(26)

式中，ε—— 浮子壁厚，mm

h—— 浮子高度，mm

n—— 浮子底部裙孔的数量

r—— 导流槽与浮子底部裙孔半径，mm

n0—— 底部裙孔初始数量

r0—— 底部裙孔初始半径，mm

2) 黏性摩擦力F1

油对浮子表面的剪切力包括开槽部分和未开槽部分，先对单个槽表面受到的剪切力进行分析计算，如图18所示。

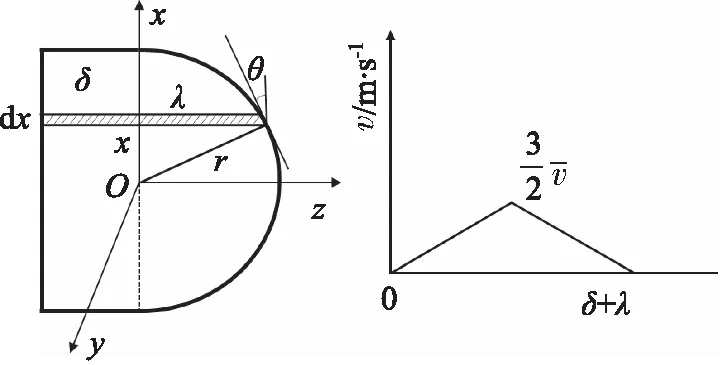
图18 单个槽剪切力分析Fig.18 Single groove shear force analysis

以槽圆心为原点O，取一微元dx，为便于计算，在分析开槽部分时，将油的流动速度看成线性分布。由之前分析平板层流的规律可得，在槽口间隙内油的速度梯度为：

(27)

δ—— 侧面间隙，mm

x——x轴上某点到槽圆心距离，mm

切应力作用面积为：

(28)

(29)

(30)

浮子表面所有开槽处受到的总黏性摩擦力F′为：

(31)

浮子表面未开槽部分剪切力作用面积为：

A=(πd1-2nr)(h-0.008)

(32)

未开槽表面受到的剪切力F″为：

(33)

则浮子表面受到的总剪切力为：

(34)

3) 油对浮子下端面及内腔顶部压力F2

此计算分析过程与之前相似，主要是因开槽而导致作用面积的改变，分析图如图6所示。

流体的连续性方程：

(35)

式中，v0—— 断流面0-0平均速度，m/s

v1—— 断流面1-1平均流速，m/s

v2—— 断流面2-2平均流速，m/s

油对浮子下端面作用面积S1的变化：

(36)

则F2为：

(37)

4) 空气对浮子上表面压力F3

参考之前的分析过程可得：

(38)

浮子侧面与阀座间隙的计算：构造函数φ(d1)=F1+F2-F3-G，绘制φ(d1)-d1曲线，观察曲线变化趋势，可知φ(d1)的零点所在区间范围为(58.525，59.000)，运用二分法的原理，求得浮子外径d1=58.860 mm，则间隙δ2=0.570 mm。对比未开设导流槽前的临界间隙0.955 mm，可知开设导流槽后临界间隙δ2减小了不少。

现分析开槽半径和数量对间隙的影响，选取不同数值代入计算，即得不同条件下的临界值。如图19为不同开槽半径r时的临界间隙δ2，图20为不同开槽数量n时的临界间隙δ2。

由图可知，浮子开槽半径r和数量n增大时，浮子与阀座的临界间隙值δ2均逐渐减小。