多路阀结构设计与改进
2022-06-09周思聪宇2战东毅张瑞轩张端政
周思聪,张 宏,卢 宇2,战东毅,张瑞轩,张端政
(1.大连理工大学 机械工程学院,辽宁 大连 116024;2.宁波江北宇洲科技有限公司,浙江 宁波 315000)
引言
多路阀是多联换向阀集成于一体的多功能换向阀,整体采用统一的模块化设计,可以为工程器械的制造者提供可靠的系统解决方案,在工程机械中有着广泛应用[1-3]。在多路阀中,稳态液动力是影响其性能的关键因素,其本质为液流通过阀口时在壁面等处所损失的动量造成的力。当多路阀中通过流量较大时,稳态液动力较为明显,会对多路阀阀芯的操控性能产生较大的影响,易出现液动力大于操控力而使阀芯动作失效的情况[4-5]。因此,稳态液动力一直是多路阀研究的重点问题,不少国内外学者对此通过仿真模拟试验进行了研究。
王林翔等[6]对滑阀内部不同流道布置情况下的流动过程进行了分析与比较,得到通过改变阀的进出油口与沉割槽的相对尺寸与位置可以减小液动力。方文敏等[7]对U形节流槽多路阀进行了仿真和试验,验证了对于多路阀稳态液动力仿真的可靠性。蔡超英等[8]研究了阀座锥角和阀芯锥角对于比例溢流阀性能的影响。SIMIC M等[9]通过试验和仿真相结合的方式,探讨了滑阀节流口处射流角度和结构尺寸对于湍流特性以及液动力等的影响。LISOWSKI E等[10]对电磁阀阀芯进行了研究与分析,探究了阀芯的受力与阀体内单位体积流量的关系。有学者通过大量试验测试了3种不同结构形式的阀芯节流槽在不同阀芯开口度、不同流量下的射流角度、液动力、流量系数以及阀口过流面积等重要参数[11-12]。王晓凯[13]对滑阀阀芯的径向稳态液动力进行了研究,提出对于滑阀卡紧力进行补偿。
综合上述内容分析,现有的多路阀结构改进会大幅改变原有多路阀压力流量特性,无法满足原本工作需求,且在稳态液动力方面改进程度较低,无法有效降低阀芯受力从而提高多路阀整体稳定性。因此本研究主要采用仿真和试验相结合的方式,分析原有多路阀特性,提出改进方案并对具体参数进行分析,结合流量损失和改进程度选出最佳方案,从而大幅提高多路阀的性能和稳定性。
1 试验与流场仿真对比分析
1.1 流道模型
本研究选择SDCV160-25-02-01型号多路阀进行分析研究。多路阀主要由首联、尾联和基本联3个部分组成,其中基本联的数量可以根据工程的实际需求进行增减。图1为多路阀流道结构,其中P口为多路阀进口,T口为多路阀出口,A口和B口分别与所控液压元件的油液入口和油液出口相连。

图1 多路阀流道结构Fig.1 Multi-way valve channel structure
为了模拟试验中A口、B口之间空负载的工况,在建模中增加U形管道将A口与B口相连接,并通过ANSYS DM抽取流道,如图2所示,并利用ANSYS Meshing 软件对其进行网格划分。采用分块多区的划分方法,对于结构较为规整的部分采用大体积的六面体网格;对于结构形式复杂的部分采用四面体网格并对局部进行加密;同时,在仿真中重要的部分是阀芯和流体之间相互接触的表面,所以对分界面进行局部加密,并且添加边界层,从而更好的模拟流固交界表面。网格质量参数Skewnes平均值为0.22,越接近0代表网格质量越好,标准差为0.11;Orthogonal Quality平均值为0.86,越接近1代表网格质量越好,标准差为0.08;网格节点为227845个,网格总数1108968个,该网格质量较高,符合计算条件。计算模型选取Realizablek-ε湍流模型,该模型比湍流黏性方程增加了1个公式,以及对耗散率方程做出调整,使得该模型在强流线弯曲、漩涡和旋转流场中有更好的适应性,在多路阀流场仿真分析和稳态液动力预测中具有更好的表现。采用质量入口和压力出口,流动介质为不可压缩非牛顿流体,其流体密度为850 kg/m3,运动黏度为4×10-5m2/s。

图2 ANSYS DM 抽取的多路阀流道Fig.2 ANSYS DM extraction of multi-way valve channel
由于单一的数值模拟方法无法验证仿真模型的准确性,所以本研究采用试验和仿真相结合的方式进行研究。以试验数据为基准,利用仿真数据拟合试验数据,选取合适的湍流模型和边界条件等,以校正仿真参数,减少误差。
1.2 多路阀阀芯受力测试
采取试验测试与仿真模型相对照的方法验证仿真正确性,试验中需要测试P,T,A,B 4个阀口的压力值以及阀芯在不同流量和开度下受力的情况,试验原理图如图3所示。

图3 多路阀试验原理图Fig.3 Multi-way valve test schematic diagram
试验中共设置4个测压点,分别测量阀P,T,A,B 4个位置的压力情况。流量计用来监测和调整通过测试阀的流量大小,拉压力传感器用来测量阀芯受力情况。试验时A,B口之间采用无负载的连接方式。
试验时分别测量入口流量q为1.42, 1.98, 2.13, 2.27 kg/s,出口连接油箱,即出口压力为0 MPa的情况下阀芯全行程下的受力情况。试验过程中阀口的开度由固定拉压力传感器的螺纹进给台架控制,测量阀口开度间隔为0.5 mm。在每一个开度下多次测量拉压力数值,取稳定后的数值计算平均值,并分别记录P,T,A,B 4个阀口的压力,以及阀芯的受力情况。
1.3 试验与仿真对比
通过试验和仿真,选取入口流量为1.98 kg/s时,不同阀芯开口度x下的稳态液动力F大小对比如图4所示。试验结果与仿真结果基本吻合,误差仅为6.4%。因此,通过上面的分析可知,现有的模型在多路阀流场仿真分析和稳态液动力预测中具有更好的表现,基本能满足对多路阀结构设计和仿真的需求。在上述的湍流模型下,对原有的多路阀进行仿真模拟,分析其现有问题并提出改进方案,再次通过仿真与改进前对比,确定改进的合理性以及程度。
2 原多路阀仿真与分析
由上可知,所用的湍流模型与实际试验误差能够满足仿真需求,沿用上述设置,通过重新设置边界条件研究现有多路阀的流量受力特性。
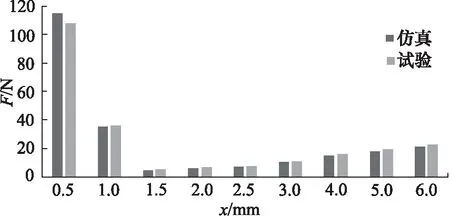
图4 仿真与试验数据对比图Fig.4 Comparison of simulation and experimental data
因此,从0~3.5 mm,以0.3 mm为间隔,从4~6 mm,以1 mm为间隔,取多个开口度下的多路阀建立模型;再分别以1 MPa为间隔,取入口p压力为10 MPa,出口压力为0.15 MPa进行模拟,得到数据并通过MATLAB的Curve Fitting工具箱进行函数拟合得开口度-受力图如图5所示。

图5 开口度-受力图Fig.5 Openness-force diagram
由图5可见,在开口度为0~3.5 mm段,即节流槽未全部打开时,稳态液动力先随开度和压力增大而增大,在2.1 mm处达到此段峰值,随后逐渐下降,到2.6 mm处再次开始增大;在3.5~6 mm段,即节流槽全部打开时,稳态液动力持续增大并在4 mm处达到全段最大值,往后随之快速下降。从理论公式上考虑,稳态液动力计算公式为:
(1)
式中,Cc—— 油液流经节流入口时的收缩系数
ω—— 阀口节流槽面积梯度
Cv—— 流体通过阀口时的速度系数
x—— 阀芯开口度
Δp—— 阀口处压力差
θ—— 射流角度[14]
图6、图7分别为2.1,4.0 mm开口度速度云图。由图可知,随着开口度增大,射流角度也随之减小,而不是传统理论认为的保持69°;由图7可以看出,随着射流角度减小,液流在节流口处的速度损失也会减小,更快地冲击在阀芯右侧端面上,造成能量损失,使得阀芯受力大幅增大。

图6 2.1 mm开口度速度云图Fig.6 2.1 mm opening velocity contour
由上可知,对于此多路阀的改进重点在于降低其稳态液动力的峰值,即2.1 mm及4.0 mm处阀芯所受稳态液动力。将对此提出一种环形凸台的改进方案,以解决稳态液动力过大的问题,并对凸台相关参数进行研究。
3 改进方案对比分析
3.1 改进方案参数
针对上述问题,本研究提出一种环形凸台的改进方案,以此达到降低稳态液动力峰值目的,如图8所示为改进的环形凸台结构。

图7 4.0 mm开口度速度云图Fig.7 4.0 mm opening velocity contour
其中,x为阀芯开口度,D为多路阀通径,a为多路阀P口到A口段(即B口到T口段)阀体厚度。d为环形凸台直径,L2为所述环形凸台厚度,R为所述环形凸台加工圆角。本研究使用的多路阀通径D为22 mm,阀体厚度a为9 mm。

图8 环形凸台结构Fig.8 Annular boss structure
为了确保环形凸台能够在开口度2.1 mm处生效,L2
3.2 改进方案的选择
对装配13, 14, 15,16,17 mm 5种尺寸环形凸台阀芯的多路阀抽取流道并进行仿真模拟,压力入口取10 MPa,出口压力恒定为0.15 MPa,开口度取0.9, 1.5, 2.1, 2.6, 4.0,6.0 mm进行研究,计算出各直径环形凸台改进情况如表1所示,得到流量特性对比曲线图和流量-稳态液动力对比曲线图,如图9、图10所示。

表1 各直径环形凸台改进情况Tab.1 Optimization of each diameter annular boss
由图9和表1各直径环形凸台改进情况可见,在同出入口压力差下,13 mm环形凸台在阀芯行程全段基本没有流量损失,其余环形凸台的多路阀在小开口度下,各多路阀流量基本一致,环形凸台结构基本没有造成流量损失;在节流槽全开段,环形凸台造成的流量损失随开口度增大而增大,同时随环形凸台直径增大而增大。

图9 流量特性曲线Fig.9 Flow characteristic curve
由图10和表1可见,13 mm环形凸台基本没有流量损失,但稳态液动力改进有限;14 mm流量损失较小,在最大压力差和最大开口度处仅损失0.4 kg/s流量的同时,相较13 mm环形凸台,大幅改进稳态液动力;15,16 mm环形凸台增大流量损失的同时,在稳态液动力方面没有进一步大幅的改进;而17 mm损失流量的同时,相较14 mm环形凸台,在2.1 mm开口度处改进效果较差,在4.0 mm开口度处改进效果最好。

图10 稳态液动力曲线Fig.10 Steady flow force curve
综合流量损失和稳态液动力改进两方面考虑,本研究选择14 mm直径的环形凸台作为最佳改进方案。将从速度云图方面详细分析改进原理和环形凸台直径对于流量和稳态液动力影响的原因。
3.3 改进原理与分析
环形凸台的改进原理在于将通过节流槽的高速液流通过环形凸台引导到阀体壁面上,降低了液流流速,减少了直接冲击在阀芯右端的液流量,从而降低了阀芯右端所受冲击力,降低了阀芯整体的稳态液动力。
14 mm直径环形凸台在2.1 mm开口处的速度云图,如图11所示,液流冲击在节流槽平面后,以30°的角度冲击向环形凸台并被其引流向阀体壁面,对比图6可见,大幅减少了直接冲击在阀芯右端的液流流量和流速,从而大幅降低阀芯整体的稳态液动力。
对比14 mm和17 mm环形凸台在4.0 mm开口处速度云图,如图12、图13所示,随着开口度的增大,液流的射流角度减小,直接冲击在环形凸台处的液流量增大,随着环形凸台直径的增加,冲击的液流形成的涡旋越大;同时可以观察到,在右下方环形凸台、阀芯和阀体三者形成的腔体处,形成了较改进前流速更大的涡旋,两处涡旋共同造成了流量和压力的损失。

图12 14 mm环形凸台4.0 mm开口处速度云图Fig.12 4.0 mm opening velocity contour of 14 mm annular boss

图13 17 mm环形凸台4.0 mm开口处速度云图Fig.13 4.0 mm opening velocity contour of 14 mm annular boss
3.4 试验结果对比
通过现场加工改进后的阀芯,在系统进口流量1.98 kg/s,出口连接油箱,即出口压力为0 MPa的条件下进行试验,得到原阀芯与改进阀芯试验液动力对比如图14所示。由图14可见,改进后的阀芯有效降低了整体稳态液动力,峰值改进度为30.9%,满足工程实际需求,能够显著提高多路阀的性能和稳定性,充分验证了本研究仿真模拟的准确性以及改进方案的可行性,为多路阀的改进提供了明确有效的方案。

图14 原有阀芯与改进阀芯试验对比图Fig.14 Original spool and improved spool experimental comparison diagram
4 结论
(1) 通过与试验数据相对比,对于所研究的多路阀,以试验数据为基准,采用Realizablek-ε模型稳态液动力仿真结果较为准确;
(2) 通过Fluent的仿真分析,结合MATLAB进行的压力-流量-稳态液动力三维图,发现多路阀在节流槽未全开段和全开段各存在1个峰值处,2处多路阀稳态液动力较大,是本研究改进的重点;
(3) 提出环形凸台的改进方案,并对多个直径环形凸台进行仿真分析,得出了随着环形凸台直径的增大,节流槽未全开段阀芯所受稳态液动力先降低后上升,节流槽全开段阀芯所受稳态液动力持续降低,同时流量损失逐渐增大。最终综合考虑得出14 mm直径环形凸台造成流量损失相对小,却能大幅降低稳态液动力,对多路阀改进效果最好,并通过对SDCV160-25-02-01型号多路阀的试验,验证了改进的正确性。本研究改进了多路阀稳态液动力特性,能够显著提高多路阀的性能和稳定性,为多路阀的改进提供了明确有效的方案。
