高压氢气减压器内部流场仿真分析
2022-06-09
(1.重庆大学 机械传动国家重点实验室,重庆 400044; 2.重庆大学 机械与运载工程学院,重庆 400044;3.重庆凯瑞动力科技有限公司,重庆 401120)
引言
氢燃料电池汽车作为新能源汽车之一,由于其使用氢气作为燃料并通过化学反应转化成电能供给汽车使用,反应产物主要为水,不产生任何污染性气体,因此具有零排放的优点。目前,氢燃料电池汽车多采用气态储氢方式,为了提高汽车的续航里程,一般采用以下两种方法增加载气量:一种是增加气瓶的容积,另一种是增加气瓶的压力。在气瓶的安装空间受限制的条件下,增加气瓶的压力是提高氢气储量的主要方式。
为保证一次加氢后行使距离达200 km,通常储氢压力需35 MPa以上,而要保证一次加氢后行驶距离500 km,储氢压力则要求高达70 MPa[1]。在新能源汽车未来的发展中,传统的单级减压阀无法在高压、大压力比的工况下实现压力稳定调节,会出现振动大、能耗高等一系列问题。因此近年来,许多学者对适用于高压、大压力比等环境或能实现多级降压的调压器做了研究。储景瑞等[2]设计了一种高压气动减压阀,并研究了输出压力控制精度及响应速度的影响因素。徐志鹏等[3]研制了一种高压气动比例减压阀,并研究了结冰特性对减压阀性能的影响。张春[4]研究了先导式高压气动减压阀主要参数对其能量和静动态特性的影响。刘佳等[5]研究了高压差迷宫式调节阀,采用数值模拟方法着重分析了不同流道形式对压降控速性能的影响。唐腾飞等[6]提出了一种适用于迷宫式调节阀节流碟片流道优化的设计流程,可以有效改善流道的流动特性。彭健等[7]对多级降压调节阀的阀芯结构进行了改进,改善了阀门的空化现象。
随着氢燃料电池汽车研究的开展,不少学者研究并设计了一些新型式的氢气减压阀,訚耀保等[1,8-9]研究了氢能源汽车两级超高压气动减压阀,分析其工作机理、特性,并对其内部流场分别在35 MPa,5 MPa压力下进行了二维流体仿真,流场中氢气为音速或超音速流动状态,速度较大,主要出现在节流位置下游,减压过程主要在节流位置处实现。CHEN Fuqiang等[10-11]研究了一种由1个多级减压器和1个多级消声器两部分组成的氢燃料电池电动汽车(FCEV)2步高压减压系统,对35 MPa迷宫式多级减压器进行流体仿真,并分析了多孔孔板结构参数对其内部流动特性的影响,研究发现压力降低和速度增大主要反映在阀门开口的节流部件上,孔板层数增加或者孔径减小都会降低湍流强度。QIAN Jinyuan等[12]对氢燃料电池氢气减压过程中通过多级特斯拉阀的反向氢流动进行了数值研究。李纯杰[13]研究了减压阀的减压机理,设计了一种高压氢气减压阀,对其进行了二维数值模拟计算。JIN Zhijiang等[14]为实现加氢站氢稳定减压,设计了一种用于加氢站多级减压阀,并通过分析过热蒸汽和氢气2种流体流动特性,验证其在加氢站中应用的可行性。
值得注意的是,尽管减压阀的工作气体为氢气,但为了简化计算,在以往的仿真研究中多采用理想气体做为工作介质。尽管真实气体与理想气体仿真结果会存在误差,但仿真结果也具有一定参考价值。陈晨[15]设计了一种用于燃料电池的氢氧电气比例减压阀,并针对燃料电池双路压差控制问题,采用理想气体仿真,对减压阀进行了控制特性研究。朱旺[16]分析对比了理想气体与真实气体状态方程的仿真结果,研究发现理想气体与真实气体的压力与速度分布基本相同,温度会受一些影响。
上述研究中,关于适用于70 MPa高压的减压器研究较少,且研究的减压器多为迷宫式,加工制造难度大,以锥阀为主减压部件的减压器数值模拟采用简化的二维模型,无法观测到整体流场的分布状态。本研究对一种以锥阀、节流孔为节流元件的两级高压氢气减压器开展了三维数值模拟,分析不同阀芯开度对其流场分布特点及流场物理参数的影响。本研究中温度对壳体产生的热应力远小于压力作用产生的机械应力,可忽略不计,因此采用理想氢气来研究其在流场中的流动特性,为氢燃料电池汽车供氢系统在高压、大压力比等复杂条件下,实现压力稳定调节提供技术支持。
1 基本原理
1.1 高压氢气减压器两级减压原理
高压氢气减压器的减压原理为节流降压,即当气体经过突缩管时,有效流动横截面积急剧减小,气体呈加速流动状态,根据能量守恒定律,压力能转化为动能,使得动能增大,压力能降低,因此,高压气体流经突缩管后可以实现节流降压。图1为高压氢气减压器两级减压示意图,高压氢气从高压腔室进入,经过阀门实现第一次减压后进入中压腔室,再经过节流孔完成第二次减压,最终低压氢气进入低压腔室。通过两级减压,实现较大减压比的高压气体减压[17]。其中,阀门开口大小由阀芯的位置确定。
1.2 流体流动控制方程
流体流动也需要满足质量守恒定律、动量守恒定律、能量守恒定律。守恒定律的基本控制方程[18]列出如下。

图1 两级减压示意图Fig.1 Schematic diagram of two-stage decompression
1) 质量守恒方程
质量守恒方程即为连续性方程:
(1)
式中,ρ—— 流体的密度
u—— 流体的速度
t—— 时间
上述连续性方程对于可压缩或不可压缩流动,黏性或无黏性流动,定常或非定常流动均可适用。当流体为定常可压缩流动时,式(1)可变为:
▽·(ρu)=0
(2)
需要提及的是,由于空气与氢气的性质、参数不同,在保证其他参数相同的情况下,空气的质量流量会大于氢气的质量流量,但依然满足质量守恒关系,因此满足本研究关于流量的趋势性分析。
2) 动量守恒方程
按照动量守恒定律,可以推导出动量守恒方程如下:
ρu·▽u=-▽p+▽·(τ)+ρg+F
(3)
式中,p—— 静压
g—— 重力加速度
F—— 除重力之外的外部体积力。计算中不考虑重力和重力之外的体积力的影响,因此ρg=F=0。
τ—— 黏性剪切应力张量,可表示为:
(4)
式中,μ—— 动力黏度
u′ —— 速度u的转置矩阵
I—— 单位张量,其余符号意义同上
3) 能量守恒方程
流体流动过程中能量守恒,表达式如下:
▽·[u(ρE+p)]=▽·[keff▽T+(τeff·u)]
(5)
式中,E—— 能量
T—— 温度
keff—— 有效传热系数
τeff—— 有效黏性剪切应力张量
方程左侧表示单位时间净流入能量,右侧分别表示传热和黏度耗散的能量转换。
4) 湍流模型
计算流体力学软件Fluent中包含多种湍流模型,其中k-ε双方程模型应用较为广泛。根据湍流黏度计算方法以及控制湍流扩散的参数k,ε的不同可分为Standardk-ε,RNGk-ε和Realizablek-ε3种模型。Standardk-ε模型对工程实际中的可压缩流动问题具有良好的求解精度,且相对节省计算量、容易收敛,该模型是一个由大量实验现象总结得到的半经验公式,湍流动能方程是通过精确的方程推导出来的,而湍流耗散率方程是由物理推理、数学上模拟相似的原形方程得到。
湍流动能k的输运方程为:

Gb-ρε-YM+Sk
(6)
湍流耗散率ε的输运方程为:
(7)
式中,xi,xj—— 流体流动方向坐标(i,j=1,2,3)
μ—— 动力黏度
k,ε—— 湍流动能和湍流耗散率
Gk—— 由于平均速度梯度产生的湍流动能产生项
Gb—— 由于浮力而产生的湍流动能产生项
YM—— 可压缩湍流中的波动膨胀对整体耗散率的贡献
C1ε,C2ε,C3ε—— 常数
σk,σε——k和ε的普朗特(Prandtl)数
Sk,Sε—— 用户自定义源项
μt—— 湍流(或涡流)黏度,可通过k和ε联合计算出:
(8)
式中,Cμ—— 常数
上述方程中的常数默认值,C1ε=1.44,C2ε=1.92,Cμ=0.09,σk= 1.0,σε=1.3。
1.3 焦耳-汤姆逊效应
焦耳-汤姆逊效应(Joule-Thomson-effect)[19]描述的是当气体流经截面突然减小的节流元件时产生压降,温度随之产生变化的现象。该效应表明真实气体在节流膨胀后温度会降低或升高,导致冷效应(正效应)或热效应(负效应)。
对于理想气体,经绝热节流过程后,其温度保持不变[19],这是由于理想气体的温度仅与焓值有关,而在气体节流过程前后焓值应相等,故理想气体的温度在节流前后不变。
2 CFD数值模拟
2.1 物理模型假设
气体在减压器中的流动过程是一个复杂的变质量的过程。为了抓住问题的本质,作出如下假设:
(1) 工作介质为理想气体;
(2) 减压器中的减压过程为绝热过程[19];
(3) 气体流动为定常流动;
(4) 数值模拟考虑黏性耗散;
(5) 考虑压缩性效应;
(6) 忽略气体重力对流动的影响。
2.2 仿真模型建立
为了能更好的运用高压氢气减压器,采用仿真软件Fluent对其内部流场进行数值模拟。图2所示为减压器三维模型,根据三维模型的内腔结构特征,利用ANSYS Workbench中SCDM模块通过体积抽取命令快速抽取流体域,由于生成的流体域具有对称性,同时为了节省仿真时间,避免仿真过程中出口回流现象的影响,将流体域模型进行如下处理:① 以对称面为中心平面,取其1/2模型来进行仿真研究; ② 去除流体域模型的圆角、倒角以及反馈腔等形状复杂且对计算结果影响不大的区域;③ 将实际出口边界位置延长至30 mm处,以解决出口回流现象,提高仿真结果的准确性;流体域及其简化后的模型如图3所示。

图2 高压氢气减压器的三维模型

图3 1/2流体域模型Fig.3 1/2 fluid domain model
2.3 网格划分
使用ANSYS Workbench中自带的Mesh模块进行流体域网格划分,图4所示为流体域的网格划分模型,考虑到内部流场结构比较复杂,因此不规则区域采用Automatic Method自动生成四面体网格。对于入口端、出口端的规则区域,为了避免网格数量过多,减小仿真模型计算负荷,均采用Sweep方法生成网格。由于阀口处压力梯度较大,该处网格质量较低会导致计算结果发散,因此对阀口进行局部网格加密处理,设置局部网格尺寸为0.05 mm,以保证网格质量。本研究中,仿真模型的网格质量以偏斜度(Skewness)作为评价指标,文中涉及的所有流体计算域模型网格偏斜度均小于0.75。
网格数量对仿真计算有着重要的影响,网格数量越多,计算结果并非越精确,且需要更多的计算资源。为确保仿真计算结果的准确性,减少计算资源的消耗,对流体域网格进行网格无关性验证。本研究以60%阀芯开度为例,通过分析不同网格数量对质量流量变化的影响来进行验证,当质量流量不随网格数量增加而变化时,即可以忽略网格对仿真计算结果精度的影响。由于70 MPa高压数值模拟需要较高的时间成本,因此选择较低的压力进行网格无关性分析,即入口压力5 MPa,出口压力1 MPa。
图5为不同网格数量对应的质量流量图,图中网格数量从17万增加到162万。由图可以看出,随着网格数量的不断增加,质量流量qm变化逐渐趋于平缓,当网格数量达到112万后,质量流量波动仅为0.07%,基本保持不变,此时可以忽略网格数量n对仿真计算结果精度的影响,故选择112万的网格数量进行数值模拟仿真。

图4 网格划分模型Fig.4 Meshed model

图5 网格数量-质量流量Fig.5 Grid quantity-mass flow rate
2.4 求解模型和边界条件
1)求解模型设置
采用基于压力(Pressure-based)求解器,进行稳态计算。由于气体在流场中的流动速度较高,流动状态比较复杂,故选择湍流模型来进行求解,湍流模型选择标准k-ε模型,该模型是工程中常用的湍流求解模型,对气体仿真有较好效果,可靠性较高。设置流体材料属性,减压器内的氢气为等熵可压缩流体,因此将氢气设置为理想气体,采用理想气体状态方程,此时Energy选项默认打开。操作压力(Operating Conditions)设为0。最后选用压力-速度耦合算法(Coupled)求解,耦合算法求解对运算内存要求较高,但收敛速度更快。
2) 边界条件设置
由于气体在流场中为可压缩流动状态,入口边界条件和出口边界条件分别设置为压力入口和压力出口,对称平面设置为对称边界,其他边界设置为壁面。在低压压缩空气仿真中操作压力通常保持默认值,而本模型中入口压力为70 MPa高压,出口压力为1 MPa,操作压力为0 MPa。
在Fluent仿真过程中,当入口压力较高,入口与出口之间的压力差较大时,各物理参数在模拟的过程中会出现剧烈波动,导致结果发散。通过大量的模拟计算,本研究提出一种高压入口边界的加压方法,该方法适用于高压气体仿真过程,并且能有效的改善仿真收敛效果,提高仿真结果的准确性。方法实施如下:设入口最终需达到的压力70 MPa为目标压力pf,每一次入口设置的压力为pi,则加压公式可表示为:
pi+1=(pf-pi)×0.1+pi(i=1,2,3…)
(9)
式中,i—— 迭代加压次数
pi,pi+1—— 入口压力迭代i和i+1次的压力值
pf—— 目标压力
在本研究中,入口初始压力p1设置为7 MPa,之后按照式(9)进行逐次迭代加压,直到入口压力达到目标压力70 MPa。
值得注意的是,高压氢气经减压器降压后并不是直接进入燃料电堆,还要经过减压器出口连接的引射器,通过引射器将氢气喷入燃料电堆,最终进入电堆的氢气压力约为0.2 MPa。仿真的出口平均压力基本稳定在1 MPa左右,而在整个对称平面的压力分布中,最低压力并不是1 MPa,但这一操作不影响压力结果及整个压力场的分布。
3 仿真结果分析
本研究对高压氢气减压器进行了稳态数值模拟求解,求解过程中气体流动状态不随时间变化,为了更好的观察气体在流场内部的流动情况,研究压力、速度等物理参数的分布,数值仿真以阀芯开口量大小(阀芯开度)为主要变量进行研究,根据阀芯开度的不同分别进行了5组算例,各组算例对应的参数见表1。
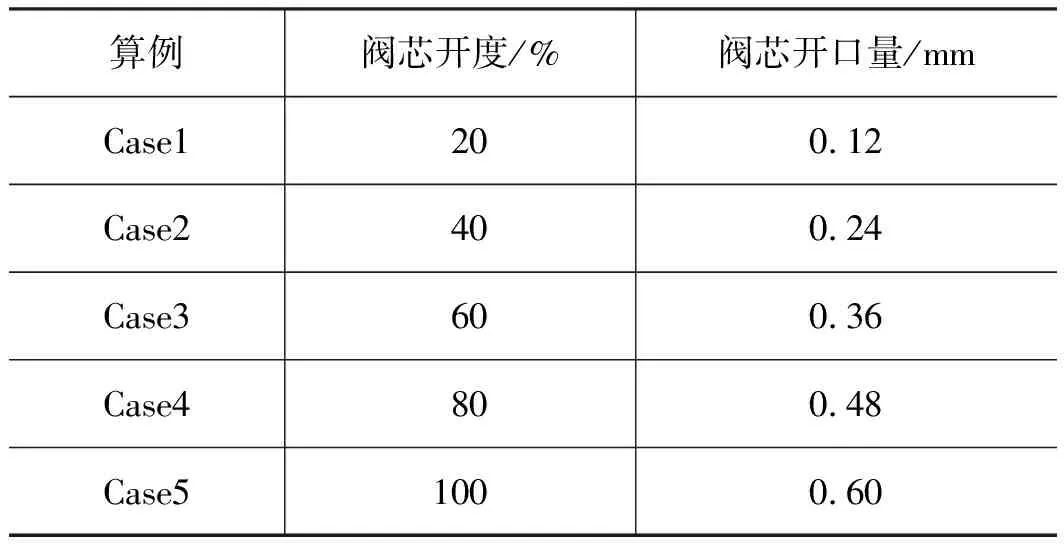
表1 不同算例参数Tab.1 Parameters of different calculation examples
3.1 压力场结果分析
通过对5组算例分别进行求解,得到不同阀芯开度下对称平面的压力分布云图如图6所示。由图6可知,高压氢气减压器在工作过程中,压力下降主要发生在阀口和节流孔处,在入口腔和出口腔压力分布都较为均匀。随着阀芯开度的增大,阀口处的压力梯度较小,这是因为阀芯开度越大,氢气流过阀口处的流动阻力越小,因此,该处的压力梯度随着阀芯开度增大不断减小。节流孔处则与阀口处相反,随着阀芯开度的增加,该处压力梯度变大。

图6 不同阀芯开度下对称平面的压力分布Fig.6 Pressure distributions in symmetry plane under different valve openings
为准确了解阀芯开度变化对压力大小的影响,对不同阀芯开度下Z方向上的压力进行研究(Z方向为入口、出口的轴线方向),做出不同阀芯开度的压力图如图7所示。由图7可以看出,在Z=25~35 mm处和Z=40~50 mm处出现压力降低,该位置即为阀芯与节流孔的位置。对应20%,40%,60%,80%,100%不同阀芯开度,氢气流经阀口后压力从70 MPa分别降到9.73, 18.72, 27.61, 35.55, 41.71 MPa;氢气流经节流孔后压力分别从9.73, 18.72, 27.61, 35.55, 41.71 MPa降到1.00 MPa。随着阀芯开度增大,阀口压降梯度减小,节流孔压降梯度增大,即第一级减压比减小,第二级减压比增大。为了确定两级减压比之间的关系,给出了不同阀芯开度下第一、二级的减压比,见表2。

图7 不同阀芯开度下Z方向上的压力Fig.7 Pressure in Z direction under different valve openings

表2 不同阀芯开度下的减压比R1,R2Tab.2 Decompression ratio R1 and R2 under different valve openings
根据表2中第一、二级减压比R1,R2的数值,可以得出高压氢气减压器的两级减压比关系满足:
R=R1×R2
(10)
式中,R—— 总减压比
R1—— 第一级减压比
R2—— 第二级减压比
由于5组算例的入口、出口边界设置均相同,即R保持不变。则根据式(10)可知,当R为定值时,R1与R2成反比,说明第一级阀口减压作用减弱,会导致第二级节流孔减压作用增强。
此外,根据图7中的放大区域可知,随着阀芯开度的增大,阀芯上游压力波动越大,对阀芯平衡影响越强,是阀芯受力不稳定的因素之一。
3.2 速度场结果分析
流场中速度的分布可以直接反映氢气在流场中的流动情况。因此,本研究以高压氢气减压器不同阀芯开度对速度场的影响展开研究,速度分布云图如图8所示。
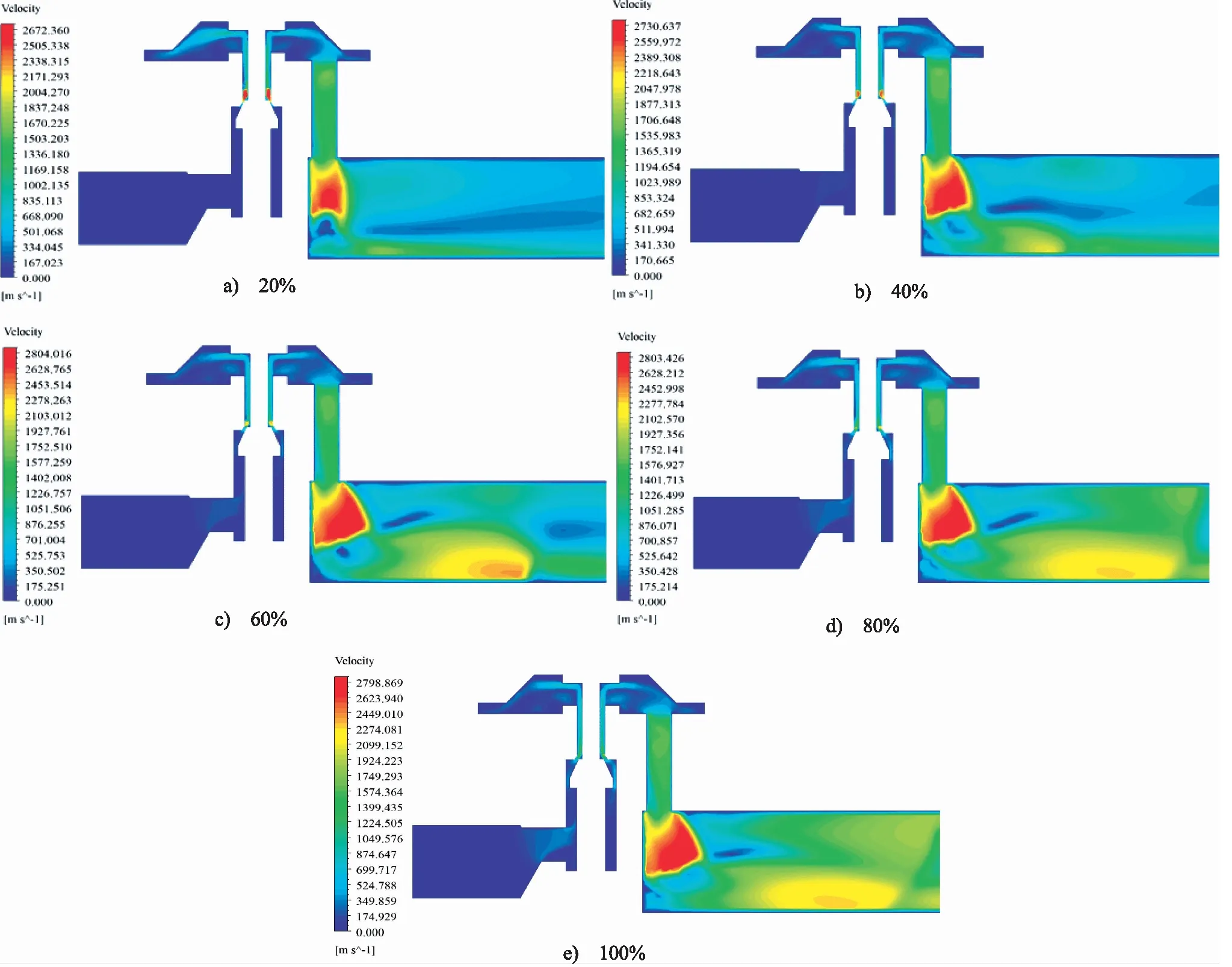
图8 不同阀芯开度下对称平面的速度分布Fig.8 Velocity distributions in symmetry plane under different valve openings
图8中在阀口与节流孔出口两处,速度有显著增大的区域,这是因为阀口、节流孔的通流面积变小,氢气在流经阀口和节流孔时经历绝热压缩过程,压力降低,导致速度增加。节流孔出口的速度突然增大,这是由于氢气在高压差条件下通过节流孔形成了高速喷射流,且由于压力降低,氢气迅速膨胀,氢气流出了节流孔后会继续加速一段距离,由于出口空间较大,速度降低极为迅速,这与文献[8]、文献[13]关于速度场分析的结论基本一致。氢气高速喷射流长时间冲击减压器壳体壁面,会对壳体造成破坏,这为研究壳体优化,减小喷射流提供基础。
从图8可以看出,不同阀芯开度下速度分布不同,且随着阀芯开度的增大,阀口处的速度及其变化区域逐渐减小,而节流孔出口的速度及其变化区域逐渐增大,这说明速度的变化受截面突变程度的影响,截面突变程度越大,速度变化越明显,且最大速度是出现在截面突变程度最大的位置,与文献[10]中的结论相符。分析最大速度的变化,图8中不同的阀芯开度,最大速度出现的位置不同,这是由于阀芯开度增大会导致阀口过流面积增加,从而减小了阀口处截面变化梯度。当阀芯开度为20%时,阀口处的截面变化梯度最大,最大速度出现在阀口处,当阀芯开度为40%,60%,80%,100%时,截面变化梯度最大位置均在节流孔处,因此最大速度均出现在节流孔出口处。
此外,研究了不同阀芯开度下Z方向速度v分布的变化,如图9所示。图中5种不同开度下阀口处的最大速度分别为2705, 2531, 2388, 2227, 2040 m/s。由此可见,随着阀芯开度的增大,阀芯处的最大速度在相应减小,这是由于阀芯开度的增大导致阀口处截面突变程度降低导致的。

图9 不同阀芯开度下Z方向上的速度Fig.9 Velocities in Z direction under different valve openings
3.3 温度场结果分析
当流体流过高压氢气减压阀中的阀口与节流孔时,属于绝热等熵膨胀过程,会导致温度的急剧下降。以20%阀芯开度为例对温度场进行分析,图10中入口、出口温度基本保持不变,这与理想气体的焦耳-汤姆逊效应相合符。结合图10与图8可知,最低温度与最大速度位置相对应,最低温度约为93 K。氢气的结霜点为14 K[13],由此可以判断低温区的存在不会导致氢气在阀芯和节流孔处结霜,因此,对高压氢气减压器性能不产生影响。其他开度下的最低温度与20%开度时差别不大,此处不再赘述。

图10 20%阀芯开度下的温度分布Fig.10 Temperature distribution under 20% valve opening
3.4 流量及能耗分析
研究质量流量和阀芯开度的关系,分别对5组不同阀芯开口量s的流场进行仿真,分别为 0.12, 0.24, 0.36, 0.48, 0.60 mm,记录进出口的质量流量值如图11所示。由图11可知,随着阀芯开口量的增加,质量流量不断增大,质量流量的变化趋势与文献[20]的结果基本一致。
湍流耗散率ε是表征湍流所产生能量消耗的物理量,湍流耗散率ε越大,意味着湍流越大,能量消耗越大。图12为不同阀芯开度下Z方向上的湍流耗散率,从图12可以看出,湍流耗散率出现了2个峰值,分别对应阀口处和节流孔处2个位置,其中第1个峰值由于阀芯阻断了流体而被分为了2个部分。湍流耗散率的峰值位置与涡旋产生的位置基本一致,由此可以从能量上验证阀口和节流孔处涡旋区域的存在。图12中,随着阀芯开度的增加,阀口处的湍流耗散率降低,与之相反的是随着阀芯开度的增加,节流孔处的湍流耗散率增大。因此,较大的阀芯打开度意味着流量损失较小,与文献[14]中湍流耗散率的结论相吻合。
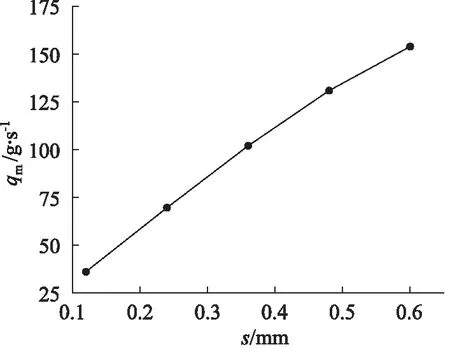
图11 不同阀芯开口量下的质量流量Fig.11 Mass flow rates under different valve openings
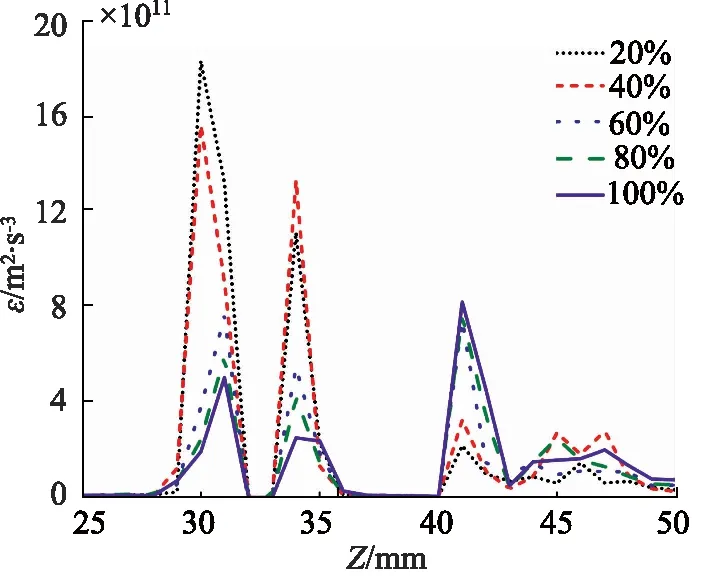
图12 不同阀芯开度下Z方向湍流耗散率Fig.12 Turbulence dissipation rates in Z direction under different valve openings
4 结论
研究了一种可用于氢燃料电池汽车供气系统的两级高压氢气减压器,通过数值仿真研究其内部流场物理参数的分布,并以阀芯开度为主要研究变量得出了流场内部压力、速度、能耗等参数的变化规律:
(1) 在减压器内部流场中,压力降低和速度增加主要反映在阀口与节流孔2个位置,随着阀芯开度增大,阀口的减压作用减弱,节流孔的减压作用增强;阀芯开度越大,阀口处最大速度越小,阀口处的速度及其变化区域越小,节流孔出口处的速度及其变化区域越大;
(2) 氢气流经阀口与节流孔后,入口温度与出口温度基本保持不变,符合理想气体的焦耳-汤姆逊效应,且流场内部最低温度与最大速度位置相对应,最低温度高于氢气的结霜点;
(3) 阀芯开度对质量流量与能耗有较大影响,质量流量随阀芯开度增大而增加;随着阀芯开度增大,阀口处的湍流耗散率减小,节流孔处的湍流耗散率增加。
