渗流流态分析在致密储层压裂诊断中的研究与应用

敬季昀，刘长龙，兰夕堂，邹剑，张璐，张丽平

（中海石油（中国）有限公司天津分公司，天津 300459）

0 引言

水力压裂是目前有效开发致密储层的关键技术。通过压裂诊断获取目标储层裂缝延伸特点、地层及裂缝参数，对提升压裂开发效果十分重要［1-4］。压后压降分析是压裂诊断的主要内容之一［3-7］，根据压后裂缝闭合状态可分为闭合前分析与闭合后分析，相应的G与F函数分析方法是目前应用最广泛的分析手段［7-8］。

Nolte［9］基于卡特滤失方程建立了 G函数，Barree等进一步完善了G函数分析曲线以识别各种非理想化裂缝特征，包括沟通天然裂缝、停泵后裂缝继续延伸、缝高突破隔层或形成多条人工裂缝等［10］，但该方法存在的问题为：诊断曲线坐标轴中的G函数及其导数相对复杂，对数据误差较敏感，对数据精度要求较高（最大误差±0.01 MPa）［8］，利用精度较低的地面压力监测数据常难以绘制理想曲线；未考虑停泵初期近井摩阻、井筒储集效应等因素的影响，而使用停泵时井底压力粗略代替瞬时停泵裂缝压力［9］，给求取裂缝净压力带来误差；缝高突破隔层和形成的多条人工裂缝具有相同的曲线特征，无法进一步区分［10］。

G函数分析方法仅用于裂缝闭合前压降分析［3-7］，Nolte等基于热扩散与压力传导的相似性及Horner压降模型建立了F函数，以用作闭合后压降分析［11］，但F函数分析方法的假设条件为压后停泵时间至少为裂缝闭合时间的2.5倍以上［11］，且不能区分闭合后双线性流与线性流，因此缺陷明显。

针对以上问题，本文提出了一种基于储层压后渗流流态分析的压裂诊断方法。该方法降低了诊断对现场压力数据精度的要求，在获取瞬时停泵裂缝压力与施工净压力时不受近井摩阻等因素的影响，实现了对多裂缝的准确识别和支撑裂缝导流能力的定性分析，将裂缝闭合前、后分析合为一体，避免了闭合后分析对停泵时间过长的假设。现场实践表明，该方法可以有效弥补现有方法的不足，为现场压裂施工提供快速、准确的诊断分析。

1 基于渗流流态分析的压裂诊断方法

1.1 基本原理

图1展示了压后压降观测期间的井口压力历史。压裂停泵后，缝内液体在高压下继续向地层滤失，裂缝-地层系统首先出现短期的双线性流，然后转变为线性流直至裂缝闭合（或闭合于支撑剂上）［12］。裂缝闭合后缝宽不再变化，缝内液体停止滤失［3］。由于储层流体与岩石的压缩性，此时在裂缝周围形成了一个高于原始地层压力的区域，该区域压力继续向远处地层传导，地层逐渐出现闭合后双线性流或线性流，若关井时间足够长，地层将出现拟径向流［13］。不同渗流流态下的裂缝表现出不一样的压力响应特点，分析这些特点可以获取多项裂缝及储层信息［3-14］，从而更好地评价储层压裂特征。

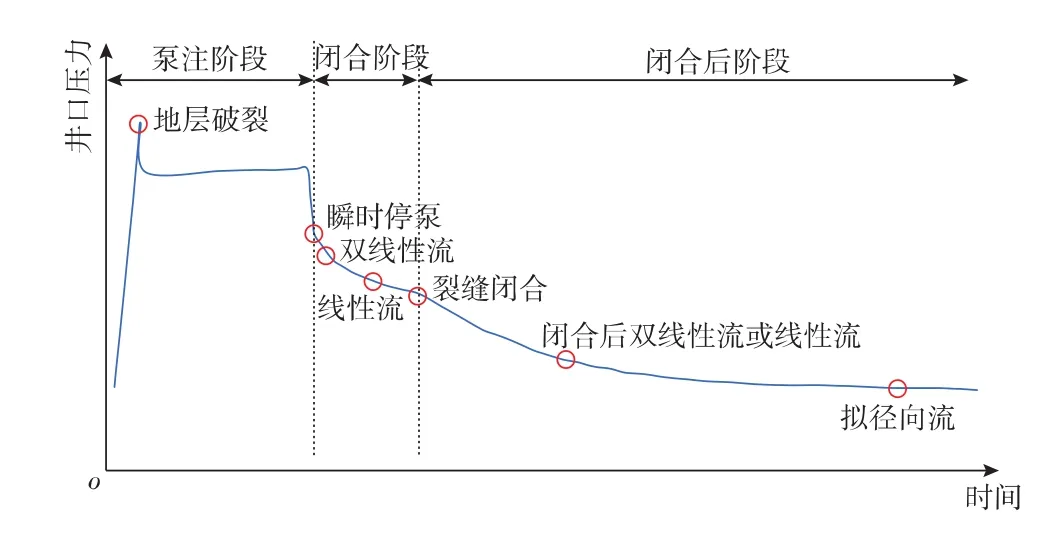
图1 压后关井期间井口压力变化示意

1.2 裂缝闭合前渗流流态分析

停泵初期，人工裂缝将产生短期的双线性流，即缝内液体滤失的同时缝长方向也存在压降。双线性流后裂缝将出现线性流特征直至闭合，这个阶段仅存在缝内液体的线性滤失［12］。Koning 和 Niko 等［15］考虑这一时期的渗流特征与裂缝储集效应，得出了相应的裂缝压力pD。

式中：K为储层有效渗透率，μm2；Kf为裂缝有效渗透率，μm2；h 为储层厚度，m；tp为压裂泵注时间，h；Δt为停泵压降时间，h；pf（tp）为瞬时停泵裂缝压力，MPa；pf（tp+Δt）为停泵期间裂缝压力，MPa；q 为压裂施工排量，m3/d；μf为压裂液滤液黏度，mPa·s；B 为压裂液体积系数；φ为储层有效孔隙度；ct为储层综合压缩系数，MPa-1；Lf为裂缝长度，m；Wf为裂缝宽度，m；Cfbc为裂缝储集效应常数［16］，m3/MPa。

致密储层岩石硬度常较高，CfbcD趋近于 0［16］，裂缝储集效应影响较小，因此可将式（1）、式（2）近似写为式（3）、式（4）。

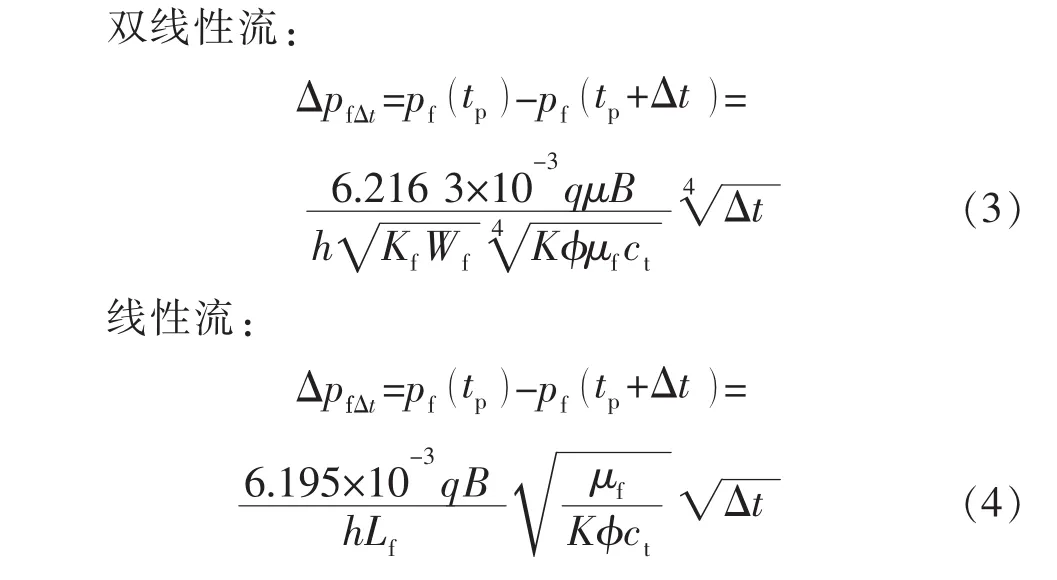
式中：ΔpffΔt为停泵期间裂缝压降，MPa。

式（5）、式（6）中的瞬时停泵裂缝压力因停泵初期孔眼摩阻、近井摩阻、井筒储集效应的影响，与停泵时井底压力存在一定差值［8］。为消除未确定的停泵裂缝压力对流态识别的影响并放大压力变化特征，可对式（5）、式（6）进行求导，得到式（7）、式（8）。

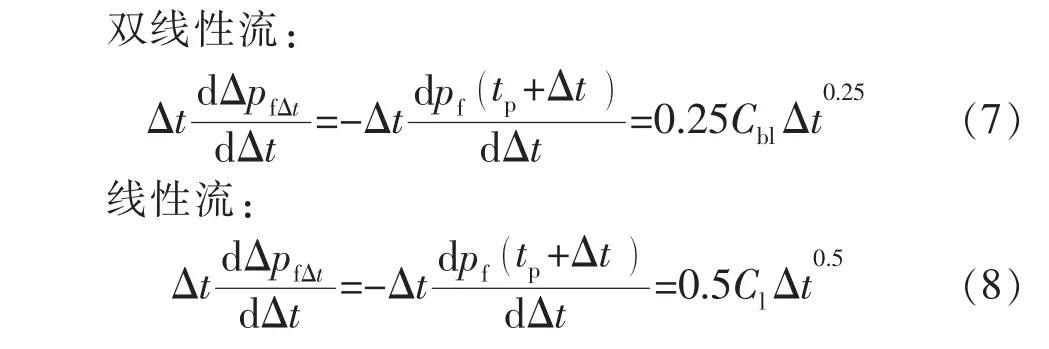
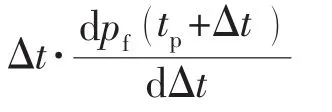
1.3 裂缝闭合后渗流流态分析

裂缝闭合后缝内压力继续向远处地层传导。此时若支撑裂缝的无因次导流能力较低 （或测试压裂的裂缝未完全闭合），储层将出现闭合后双线性流特征，即压力向远处地层传导的同时缝长方向也存在压降。若支撑裂缝无因次导流能力较高，储层将出现闭合后线性流特征，即沿裂缝不存在压降［13］。之后，若关井时间足够长（24 h 以上），地层将出现拟径向流［4］。

将裂缝视作若干瞬态线性点源，可导出裂缝闭合后的双线性流、线性流及拟径向流方程［13］。

闭合后拟径向流方程：

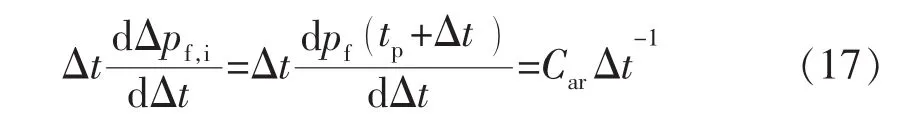
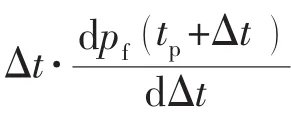
通过识别闭合后双线性流或线性流即可定性评价支撑裂缝导流能力［13］，再将对应的数据点代入式（12）、式（13）、式（14）中绘制 pf（tp+Δt）与 Δt-0.75或 Δt-0.5的曲线并线性回归，其截距即是储层原始地层压力pi。若后期观测到拟径向流，将其对应的数据点及求得的pi代入式（11）绘制 pf（tp+Δt）与 Δt-1的直线，利用直线斜率即可求解储层有效渗透率。

1.4 压后流态分析诊断曲线

对式（18）—式（22）两边取对数，可得式（22）—式（27）。

闭合前双线性流方程：

由式（23）—式（27）可知，在双对数坐标中绘制Δtdpw/dΔt与Δt的曲线并拟合不同斜率的直线段，即可识别关井期间裂缝闭合前、后的各个渗流流态，进而结合上文方法，获取瞬时停泵裂缝压力、裂缝闭合压力、裂缝净压力、多裂缝特征、支撑裂缝导流能力、储层原始压力、储层有效渗透率等信息。同时由于坐标轴简单，对数据精度要求较低，利用现场相对粗糙的地面压力监测数据即可完成分析诊断。

2 实例应用

DX-A井位于鄂尔多斯盆地东缘某致密气区块，该井太原组在主压裂后进行了压降观测，利用本文方法对其进行计算分析。储层基础数据：中深1 729.9 m，砂体垂厚15.0 m，有效垂厚9.2 m，有效孔隙度6.3%。砂体以石英为主，其次为长石，泊松比0.25，弹性模量3.3×104MPa；上下为泥岩隔层。由测井数据求得上下隔层与储层的最小水平主应力差分别为5.7，6.0 MPa。施工基础数据：φ73 mm油管泵注，泵注排量3.5 m3/min，泵注时间78 min，累计注液量261 m3，加砂30 m3，停泵时井底压力35.12 MPa，停泵后压降观测140 min。施工时利用电子压力计（最大误差±0.05 MPa），连续监测地面油管压力，同时压裂管柱底部安装高精度井下压力计（最大误差±0.001 MPa），用于试气结束后回放压力数据。

分别利用地面、井下压力监测数据绘制DX-A井G函数分析曲线（见图2，图中G是G函数，dpw/dG是井底压力对G函数的导数）。图2a中，因地面压力监测数据精度相对较低且井筒中可能存在细微扰动，导致曲线波动较大，影响分析准确性。图2b中，因井下压力监测数据精度高，绘制的曲线波动小，符合G函数分析要求。由图2b可得主裂缝闭合压力为28.37 MPa，G函数叠加导数曲线在闭合前呈明显下凹，对应的裂缝延伸特征为缝高突破隔层或形成多条人工裂缝［10］。

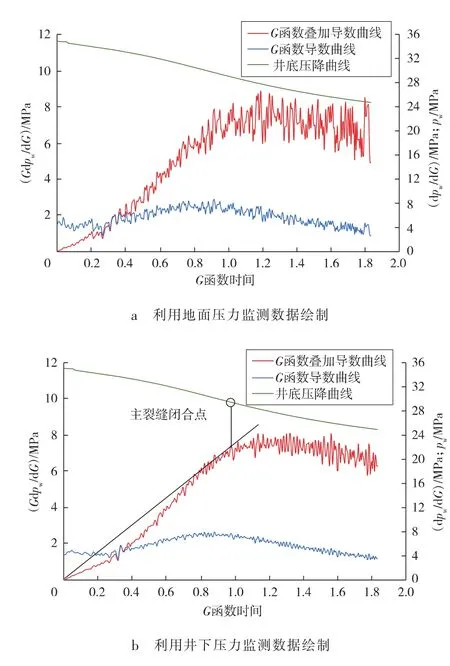
图2 DX-A井太原组压后G函数分析曲线

图2直观反映出因G函数对数据误差较敏感，导致其分析曲线对数据精度要求较高。但实际作业中，大部分施工井只进行地面压力监测，采集到的数据点相对粗糙，可能会明显影响G函数分析的准确性。再采用地面压力监测数据，绘制压后流态分析诊断曲线（见图 3）。

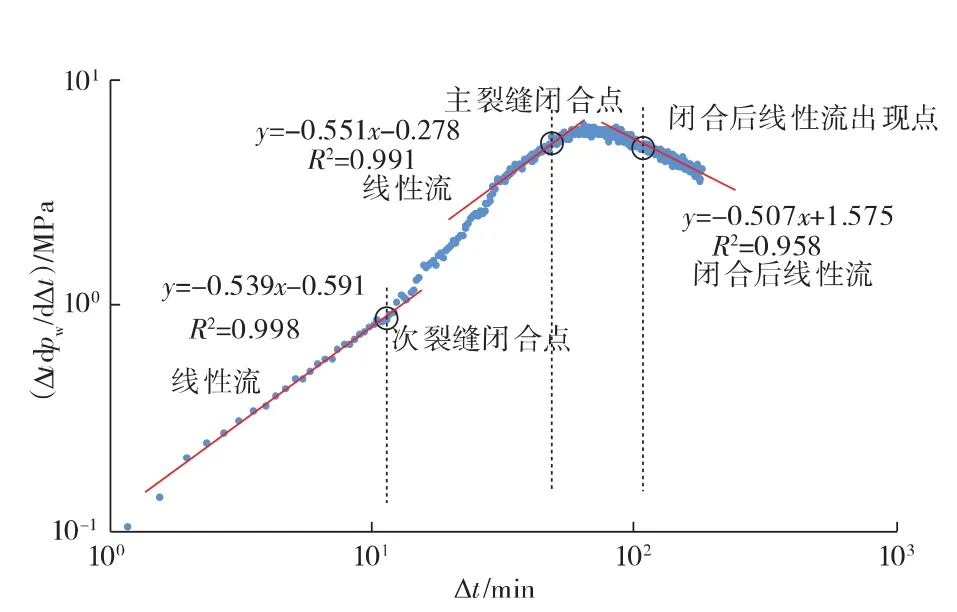
图3 DX-A井太原组压后流态分析诊断曲线

由图3可看出，由于坐标轴简单，压后流态分析诊断曲线降低了对数据精度的要求，利用DX-A井的地面压力监测数据即可绘制理想曲线。由图3可得，停泵初期因近井摩阻等因素影响未出现双线性流，但在停泵约3.5 min后出现了线性流直线段，由于裂缝储集效应的影响其斜率略大于0.5。停泵后出现2次线性流直线段，表明施工中形成了2条不同方向的人工裂缝，偏离2段直线的点分别为2条裂缝的闭合点。其中次裂缝闭合时间11.60 min，闭合压力32.87 MPa，闭合压力梯度0.019 0 MPa/m；主裂缝闭合时间58.15 min，闭合压力28.49 MPa，闭合压力梯度0.016 5 MPa/m。求得的主裂缝闭合压力与G函数曲线的识别结果基本一致。DX-A井太原组在压裂时进行了微地震裂缝监测，图4为监测成像图。监测结果与压后流态分析一致，即在不同于主裂缝方向形成了另一条人工裂缝。这不仅说明了压后流态分析的准确性，也说明图2b中G函数分析曲线出现下凹形态特征并非因为缝高突破隔层，而是施工中形成了多条人工裂缝所致。

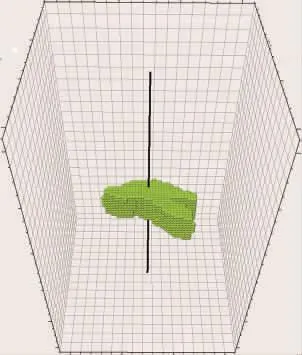
图4 DX-A井太原组微地震裂缝监测成像

将图 3识别的线性流数据点代入式（7）、式（8），绘制瞬时停泵裂缝压力识别曲线（见图5）。图5中数据点拟合程度高，说明方法可靠性强，由图中截距可得瞬时停泵裂缝压力为33.96 MPa，较停泵时井底压力小1.16 MPa，该值与主裂缝闭合压力的差值即为裂缝净压力5.47 MPa。准确求取净压力可用于进一步计算裂缝几何尺寸［6］，同时可以看出，裂缝净压力小于储隔层最小水平主应力差，进一步佐证了裂缝延伸过程中并未突破隔层。

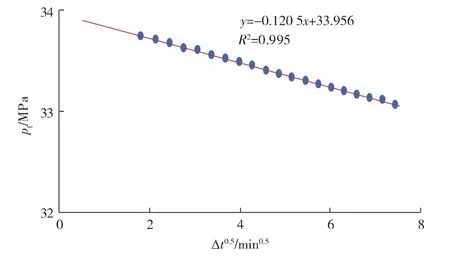
图5 DX-A井太原组瞬时停泵裂缝压力识别曲线

DX-A井太原组的压后压降观测时间（140.00 min）不足裂缝闭合时间（58.15 min）的2.5倍，不满足常规F函数的分析假设条件［11］。但由图3可知，裂缝在停泵后102.70 min即出现了闭合后线性流。出现闭合后线性流而非双线性流表明支撑裂缝呈无限导流渗流特征［13］，无因次导流能力较高，与该井所用压裂液残渣低、破胶好、携砂性能优良的实验结果相符。再将图3识别的闭合后线性流数据点代入式（12）、式（13）、式（14），绘制原始地层压力识别曲线（见图6）。由图中截距可得储层原始地层压力为16.66 MPa，折算地层压力系数0.98，与压前测试得到的原始地层压力16.80 MPa基本一致。而图3中未观测到拟径向流，探测致密储层压后拟径向流并获取有效渗透率，需实施低排量、小液量、长关井时间的微注入压降测试［3］。

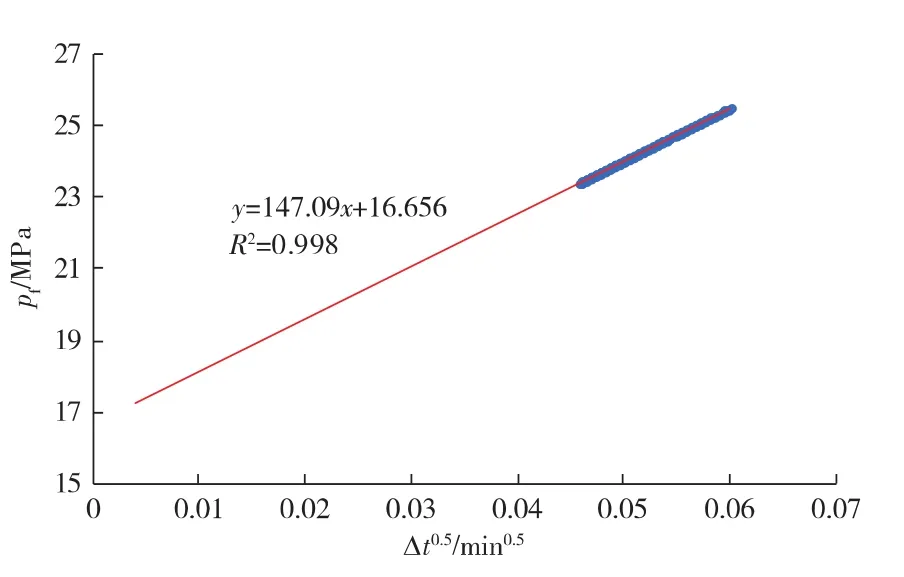
图6 DX-A井太原组原始地层压力识别曲线

3 结论

1）较常规诊断方法，本文建立的压后流态分析诊断曲线坐标轴简单，对数据精度要求较低。实例计算表明，采用现场地面压力监测数据即可绘制理想曲线，有利于对致密储层压裂特征快速分析。

2）本文方法可通过识别、拟合线性流特征直线来获取瞬时停泵裂缝压力、裂缝闭合压力、裂缝净压力及多裂缝特征。实例计算表明，该方法在求取瞬时停泵裂缝压力及裂缝净压力时不受停泵初期近井摩阻等因素的影响，同时能准确识别多裂缝特征，从而弥补常规方法在获取净压力及识别裂缝形态上的不足。

3）本文方法没有常规闭合分析中对关井时间过长的假设，且可区分闭合后双线性流与线性流。实例计算表明，在相对较短的关井时间内，该方法可通过识别闭合后渗流流态来定性评价支撑裂缝导流能力，并获取储层原始地层压力。

4）相对基于滤失方程建立的G函数分析方法，本文方法在求解储层滤失系数、液体效率、动态缝长等方面存在不足。建议在压后诊断过程中，将该方法与常规方法进行有效结合，以对储层压裂特征做出更准确全面的评价。