含制氢装置的机组组合与检修低碳协同优化研究

郭恒元，冯小峰，李国栋，段志国，李远征

（1.华中科技大学人工智能与自动化学院，武汉430074；2.广东电网有限责任公司计量中心，广州 510080；3.国网天津市电力公司电力科学研究院，天津 300384；4.国网河北省电力有限公司石家庄供电分公司，石家庄 050004）

0 引言

随着经济不断发展，各行各业对电力的需求日趋强烈。国家能源局发布的数据显示，我国全社会全年用电量从2014 年的5 520 TW·h 增长到2021 年的8 310 TW·h，每年都保持正增长。可以预见，用电量的持续增长将对电网运行的安全性、稳定性和经济性带来巨大挑战，也会对电网中的电力调度提出更高要求。另一方面，随着能源和环境问题日益凸显，新能源的应用得到了学者们广泛的关注。其中，氢能作为一种新兴的清洁能源，不仅可以用于现代工业生产，同时具有能量密度高、燃烧产物仅为水等优点，被认为是未来能量储存和供应的理想载体［1］。此外，为了减少温室气体排放、改善环境，越来越多的国家开始制定相关的环保政策，设计相关的环保机制，在这些政策和机制设计中，碳排放权交易被大量实践证明为一种切实有效的碳减排工具。自《京都议定书》制定，在各国政府的大力支持下，世界上已经建立起一些先进的碳排放交易体系［2-4］。

作为电力系统调度优化的重要部分，发电计划与机组检修计划旨在通过优化安排机组的开停机状态以达到电网安全、经济运行的目标，二者之间相互影响，且联系紧密。在传统的电力系统调度计划编制中，检修计划作为发电计划的约束条件存在，这将会限制发电计划的优化空间。为此，有学者提出机组组合与检修协同优化这一概念。Wang Y 等［5］提出了一种考虑能源约束和突发事件的机组检修调度和安全约束机组组合协同优化模型，旨在提高电力系统调度过程中的经济性和安全性。Lou X 等［6］建立了基于风险的检修调度和机组组合联合调度模型，在系统运行风险得到有效控制的同时，降低了总运行成本。李本新等［7］提出了一种发、输电检修与机组组合联合决策的Benders 分解方法。周明等［8］建立了一个基于机会约束规划的月度机组组合和检修计划联合调度的随机模型。Ge X等［9］考虑了不同能源的互补性，提出了一种风-水-热系统的中期发电与检修联合调度模型。然而已有研究只考虑了经济性目标，忽视了系统可靠性、节点电价稳定性和线路安全性等其他重要指标。

目前，已有制氢技术主要有化石能源制氢、工业副产气制氢和电解水制氢等几种。而电解水制氢具有原材料易获得、生产效率高和产品纯度高等优点，发展潜力巨大。随着催化剂研发、电解池结构优化等领域技术的发展，电解水制氢将会进一步普及应用到各个行业［10］。近几年来，世界上的几个大国高度重视氢能源的发展，大力扶持氢能的研发和产业化。国际氢能委员会（Hydrogen Council）预测，到2050年氢能在全球能源需求中的占比将达到18%。

碳交易机制的建立与完善可以加快实现电力系统减少温室气体排放的目标，而电力调度是电力系统的关键环节，因此，国内外研究都开始将碳交易机制引入电力系统，建立低碳调度模型。娄素华等［11］考虑大规模的光伏接入，建立了一种兼顾经济性、低碳性和可靠性电力系统优化调度模型。Jin J等［12］提出了一种同时考虑风电不确定性和碳排放权的随机动态经济调度模型，有助于基于碳交易机制更合理地将风电综合系统负荷需求分配到各机组。Tan Q 等［13］基于碳排放交易和可再生能源组合标准，提出了考虑价格波动的成本核算模型，并将其应用于风-光-火联合调度系统。

为求解本文提出的多目标协同优化模型，需要一种高效算法。为解决科学与工程领域中的多目标优化问题，国内外学者提出了大量的多目标优化算法，如：快速非支配排序法［14］，多目标粒子群优化算法［15］和多目标差分进化算法［16］等。针对粒子群算法难以达到全局收敛的问题，孙俊等［17］提出了一种求解效果更优、收敛性更好的量子行为粒子群算法。而量子行为粒子群算法极度依赖收缩-扩张系数的选择，算法的表现好坏很大程度上取决于该系数。目前，有学者提出了一些收缩-扩张系数的控制策略，但是这些策略不能根据当代粒子群的状态选择最优的参数［18］。如果将近些年提出的深度强化学习与量子行为粒子群算法结合，则可以通过灵活更新关键参数来提高算法的性能。

基于社会用电量不断增长、电力系统节能减排压力巨大的背景，本文考虑了电力系统需求侧存在制氢装置的情况，探究了碳交易机制下的机组组合与检修多目标协同优化问题；为了能更有效地求解模型，本文还研究了如何运用深度强化学习来改进多目标优化算法的问题。

1 碳交易下的机组组合与检修单目标协同优化模型

1.1 碳交易成本及约束

本文采用初始碳排放权免费分配中的基准线法，整个发电系统初始的碳排放限额为

式中：PD(t)为时段t 内系统的需求功率；η 为单位电量排放分配额［19］。

同时，系统中的发电机组的碳排放量为

式中：Cti为机组i的碳排放系数；PGi(t)为机组i在时段t的机组出力，T（t）为单个时段包含的小时数量。

本文将收益视为负成本，则可得到碳交易成本函数

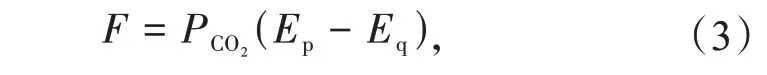
式中：PCO2为碳交易价格。

在碳交易机制中，除了会产生碳交易成本外，可用于交易的碳排放权还存在额度上限，还需考虑碳排放权交易量约束

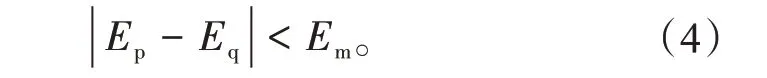
1.2 机组组合与检修单目标协同优化模型

首先，本文建立了一个碳交易机制下的月度机组组合与机组检修的单目标协同优化模型，其目标函数为

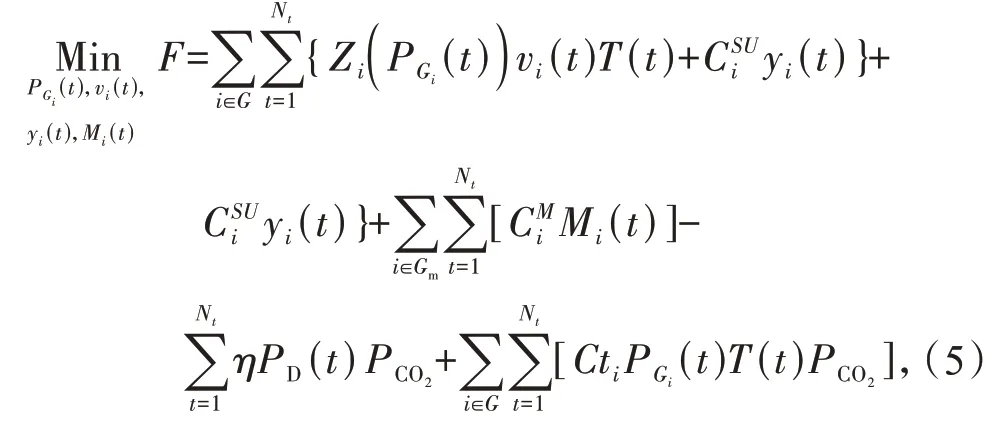
式中：vi(t)为机组i 在时段t 的工作状态变量，vi(t)取1 表示机组处于运行状态，vi(t)取0 表示机组处于停机状态；yi(t)为机组i 在时段t 的启动状态变量，yi(t)取1 表示机组在时段t 启动，yi(t)取0 表示机组未在时段t 启动；Mi(t)为机组i 在时段t 的检修状态变量，Mi(t)取1 表示机组在时段t 进行检修，Mi(t)取0 表示机组未在时段t 进行检修；PGi(t)为机组i在时段t的机组出力；G表示所有机组的集合，Gm表示待检修机组的集合；Nt表示时段的数量；T（t）为一个时段包含的小时数量；其中Zi(PGi(t)) = C0i+C1iPGi(t) + C2i(t)，C0i，C1i及C2i为机组i 的发电成本系数为机组i的启动费用；为机组i的检修费用。

该模型的约束条件有：系统功率平衡约束、机组出力上下限约束、机组爬坡速率约束、支路潮流安全约束和碳交易量约束。

（1）最小净备用量约束

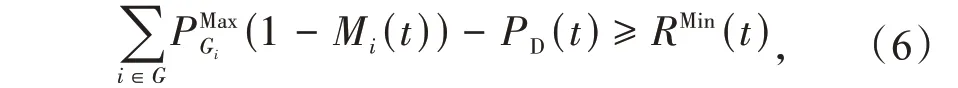
（2）同时检修机组最大数量约束

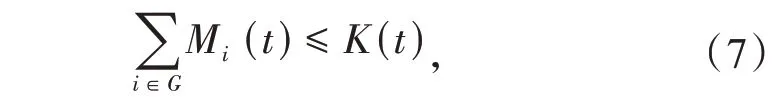
式中：K（t）表示时段t 能同时检修的机组的最大数量。

（3）检修与运行状态约束

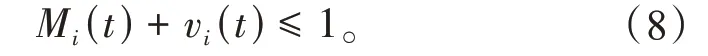
（4）最小运行时间和最小停机时间约束。

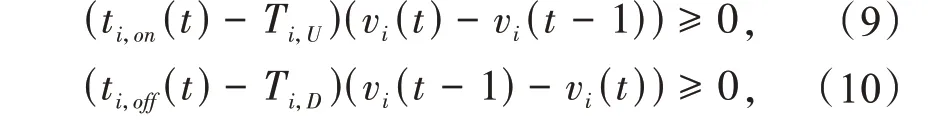
式 中：ti，on(t) 为 机 组i 在 时 段t 的 连 续 运 行 时 间，ti，off(t)为机组i在时段t的连续停机时间；Ti，U为机组i的最小连续运行时间，Ti，D为机组i的最小连续停机时间。

（5）系统功率平衡约束

（6）机组出力上下限约束

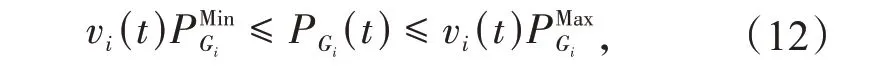
（7）机组爬坡速率约束

（8）支路潮流安全约束

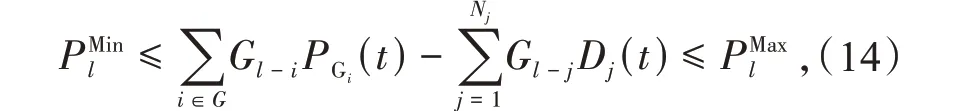
（9）碳交易量约束

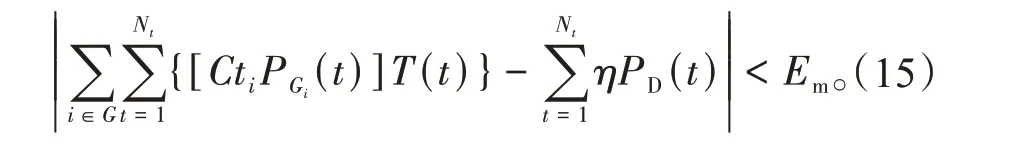
2 多目标协同优化模型与电解水制氢系统

2.1 电力供给侧

在第1 章节的基础上，本文在电力供给侧建立了一个碳交易机制下的月度机组组合与机组检修的多目标协同优化模型。为便于求解，本文建立一个双层多目标协同优化模型，其具体结构如图1所示。

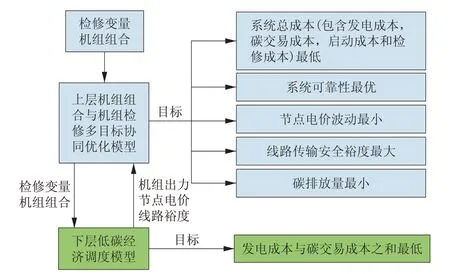
图1 多目标模型结构Fig.1 Structure of the multi-objective model

2.1.1 上层模型

考虑碳交易机制的月度机组组合与检修多目标协同优化的上层模型包含5 个目标函数。F1为系统总成本最小目标，F2为系统可靠性最优目标，F3为节点电价波动最小目标，F4为线路传输安全裕度目标，F5为碳排放量最小目标。

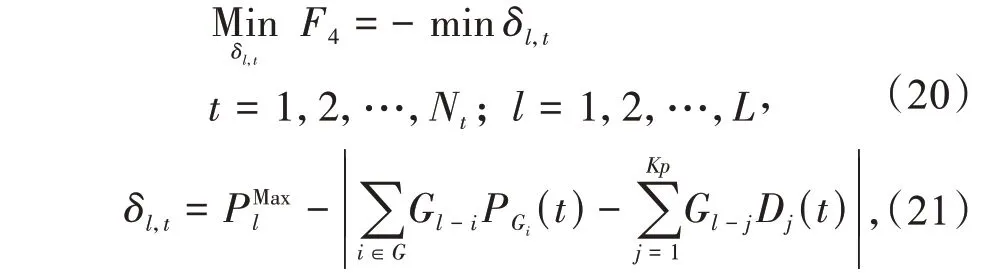
式中：δl，t为线路l在时段t的传输安全裕度；L为系统中线路的数量。

上层多目标协同优化模型约束条件与式（6）—（8）相同。

2.1.2 下层模型

下层模型为低碳经济调度模型，其目标函数如下

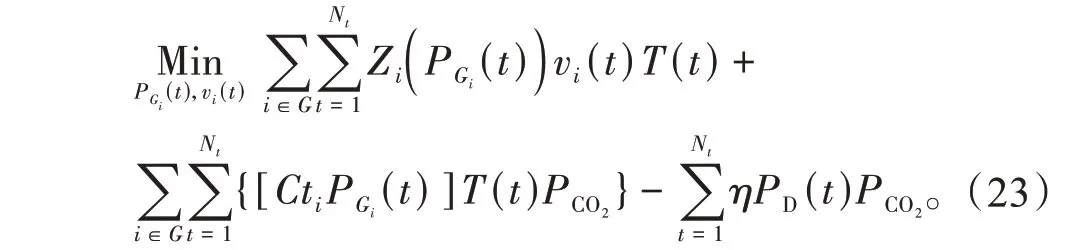
下层模型的约束条件与式（11）—（15）相同。

2.2 电力需求侧

本文考虑的电力系统需求侧中，有部分负荷用于电解水制氢系统。制氢装置的氢气产量与系统效率都与输入功率相关，氢气产量的一般计算为

式中：W 为电解水制氢系统的制氢量；P 为电解水制氢系统的输入功率；δ 为电解水制氢系统的制氢效率。

根据文献［20］的参数，可以得到典型工作日下的氢气产量与系统效率关于输入功率的曲线，如图2所示。

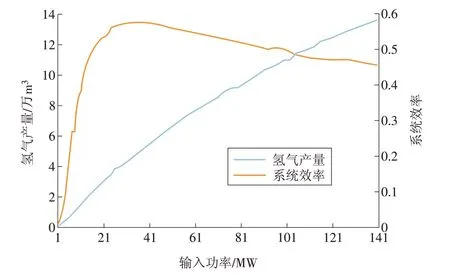
图2 氢气产量与系统效率曲线Fig.2 Curve of the hydrogen production and system efficiency

3 基于深度强化学习的多目标优化算法

3.1 收缩-扩张参数调整策略

第2 章节提出了双层优化模型，对于上层模型和下层模型需要采用不同的算法来求解。上层模型是一个多目标非线性问题，需要采用一种多目标优化算法求解；下层模型是一个二次规划问题，可以采用Gurobi商用求解器进行求解。

在量子行为粒子群（Quantum-behaved Particle Swarm Optimization，QPSO）算法中，收缩-扩张参数α 对算法的收敛速度起着决定性作用，同时很大程度的影响着帕累托解集的质量。经过大量的仿真测试，只有α < 1.781 时，才能保证QPSO 算法收敛。QPSO 算法提出之初，学者们对于收缩-扩张参数通常采用固定取值策略，即对α取一个固定值。

为了改善QPSO 算法的性能，方伟［18］对于收缩-扩张参数α提出线性递减的参数调整策略（式（25））和非线性递减的参数调整策略，其中非线性递减策略根据二次系数的正负，分为下凸的抛物线（式（26））和上凸的抛物线（式（27））。

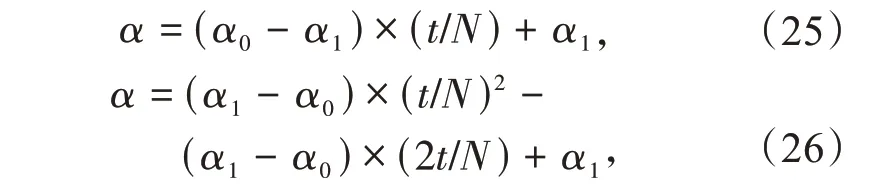
式中：α0< α1；α1为第1 次迭代时的收缩-扩张参数值，α0为最后一次迭代时的收缩-扩张参数值；N 为最大迭代次数；t为当前迭代次数。

文献［18］的仿真结果表明，4 种收缩-扩张参数控制策略（包括固定值控制策略）各有优势，在不同的测试函数中每种参数控制策略的表现不同。可见，对于未知的最优化问题，很难找到一个最优的收缩-扩张参数控制策略，往往需要采用其他更有效的方法——强化学习来对参数进行控制。

3.2 深度Q学习算法

强化学习问题通常可转化为一个由四元组｛S，A，r，p｝描述的马尔科夫决策过程（MDP）模型，其中：S是环境任务的状态空间；A是智能体执行的动作空间；r 是奖赏函数，对智能体执行动作的评价；p 是状态转移概率函数，表示某个状态s ∈S 在执行动作a ∈A，p(s´|s，a) 后 转 移 到 另 一 个 状 态s´的 概 率。MDP 模型的含义是，智能体在每一时间步t 可以感知、并获取环境的状态信息st∈S，根据获得的该信息，智能体采用相应策略从所有可能的动作集合A中选取一个合适的动作a并执行该动作。

传统的强化学习算法主要用于处理离散动作空间和离散状态空间的问题，但是现实中的模型通常是连续的。为了能解决连续动作空间和状态空间中的复杂问题，人们将强化学习和深度学习结合起来，形成了深度强化学习（Deep Reinforcement Learning）理论［21］。目前，深度强化学习算法主要分为2 种：基于值函数近似的深度强化学习算法和基于策略梯度的深度强化学习算法。这2 种算法中，最具代表性的分别是深度Q学习算法和深度确定性策略梯度算法［22］。其中，深度Q 学习算法应用更为广泛且更易实现，本节将对其作简单介绍。

深度Q 学习算法主要有2 点区别于传统Q 学习算法：

（1）训练过程中增加了目标网络（Target Network）。每隔一定的训练次数，就从Q-network 中复制网络参数到目标网络之中，因此两个网络的结构相同。在训练过程中，使用目标网络可以大大提高算法的稳定性。

（2）使用了经验池（Experience Replay Memory）技术。深度Q 学习算法中，会将训练产生的数据et=(st，at，rt，st+1)存储到经验池Buf 中，同时随机选取经验池Buf 中的数据对Q-network 的网络参数进行训练。通过这种技术手段，可以打破数据之间的强相关性，并保证算法稳定收敛。

3.3 基于深度Q学习的多目标量子粒子群优化算法

本节利用深度Q 学习方法对智能体进行训练，然后该智能体可以根据输入参数得到相应的收缩-扩张参数。该算法所使用的状态空间为NF+2 维（其中NF 为多目标模型中目标函数的个数），前NF个维度代表量子行为粒子群在该次迭代过程中的平均目标函数值，第NF+1 维度代表量子行为粒子群在该次迭代过程中的平均约束违反度值，第NF+2维度代表粒子群已经迭代的次数。该算法所使用的动作空间为PF 维，同时将算法中的´收缩-扩张´系数的范围进行PF等分，每一个等分的区域代表深度Q学习中的一个动作。智能体选择的动作落在哪个区域，则该次粒子群迭代时使用该区域范围内的一个随机数，作为收缩-扩张系数。本文中的收缩-扩张系数的取值为0.20～0.60，动作空间为20维，如果智能体选择的动作为3，则将本次迭代中的“收缩-扩张”系数为0.24～0.26的一个随机数。至于智能体的奖励值，若量子行为粒子群的当前全局最优解发生变化，则奖励为1，否则奖励为−1。

为了对该智能体进行训练，需要搭建一个深度神经网络，结合上述思路，搭建了一个4层的深度神经网络，包括1 个输入层（Input Layer），2 个隐藏层（Hidden Layer）和1 个输出层（Output Layer）。以5个目标优化模型为例，此时构建的神经网络的输入层节点个数为7，与状态空间维数相同；2 个隐藏层的节点个数分别设为36和40；输出层的节点个数为20，与动作空间维数相同；其具体结构如图3所示。

图3 神经网络结构Fig.3 Structure of the neural network

基于深度Q学习的多目标量子粒子群算法首先采用深度Q 学习对深度神经网络进行训练，训练的具体步骤如下：

（1）初始化训练最大次数tmax，当前训练次数train=1；

（2）初始化深度神经网络（Q-network），即评估网络；

（3）初始化目标网络，其参数从评估网络复制过来；

（4）初始化经验池Buf；

（5）初始化环境（量子粒子群），计算每个粒子的目标函数值及约束违反度值，得到初始最佳位置，得到最大迭代次数tmax，当前迭代次数t=1；

（6）for train=1：tmax；

（7）获得初始化状态st；

（8）for t=1：tmax；

（9）根据当前评估网络和噪声选择动作at；

（10）在环境中执行相应动作，即量子粒子群选择与动作相对应的收缩-扩张系数来进行种群迭代，同时得到奖励rt以及下一个状态at+1；

（11）将四元组（st，at，rt，at+1）存储到经验池Buf；

（12）End（第8 步骤开始的循环到此结束）；

（13）train每隔t1个迭代次数，从Buf 中选择一个最小批次的四元组来训练评估网络更新其参数，train每隔t2个迭代次数，将评估网络参数复制给目标网络；

（14）End（第6 步骤开始的循环到此结束）；

（15）保存深度神经网络（评估网络）。

重复流程（1）—（15），直到粒子群几乎在每一次迭代后都能找到更好的全局最优解为止，就可以得到一个训练完成的评估网络。将当前粒子群的相关参数，即平均目标函数值，平均约束违反度值和迭代次数，输入到该深度神经网络，可以得到一个20 维的输出，分别代表了采取20 个不同的收缩-扩张参数带来的累计奖励值。根据输出结果，从20 个参数中选取累计奖励值最大的一个作为粒子群的参数。

改进的多目标量子行为粒子群算法流程如图4所示。

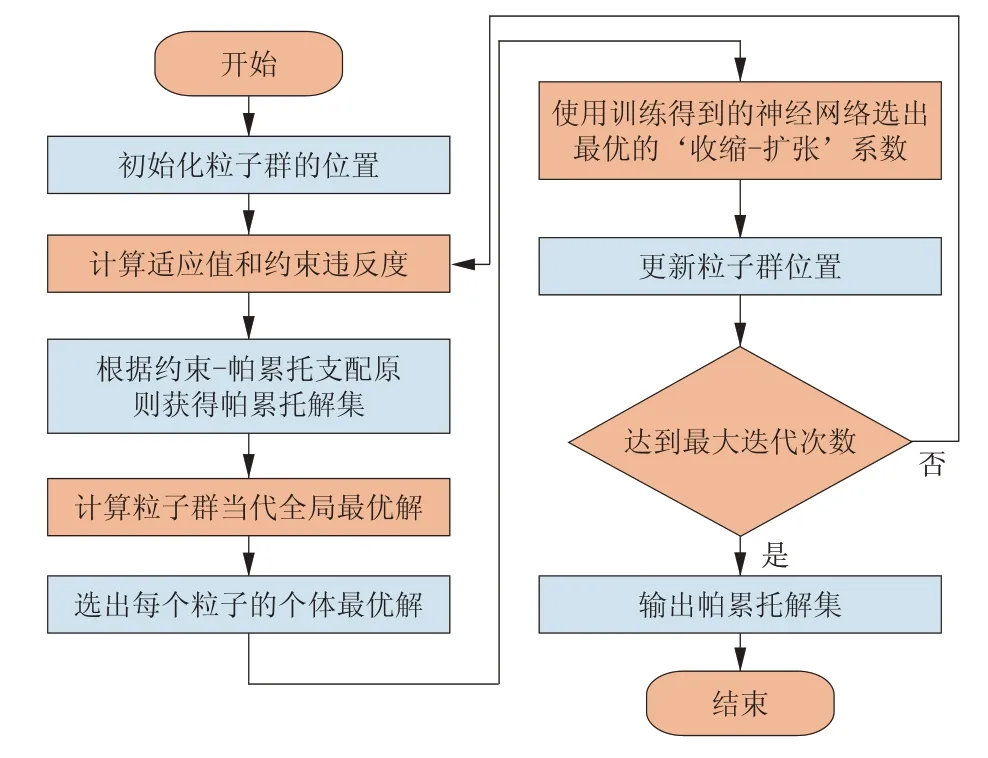
图4 改进算法的运行流程Fig.4 Operation flow chart of the improved algorithm

4 算例分析

4.1 IEEE-118节点系统参数

本文采用的IEEE-118 节点系统包含118 个节点、186 条线路以及32 台机组，其中有10 台机组需要检修。算例仿真系统月内每天的负荷量如图5所示，系统中的机组成本参数见文献［23］，机组的其他信息见表1—2。

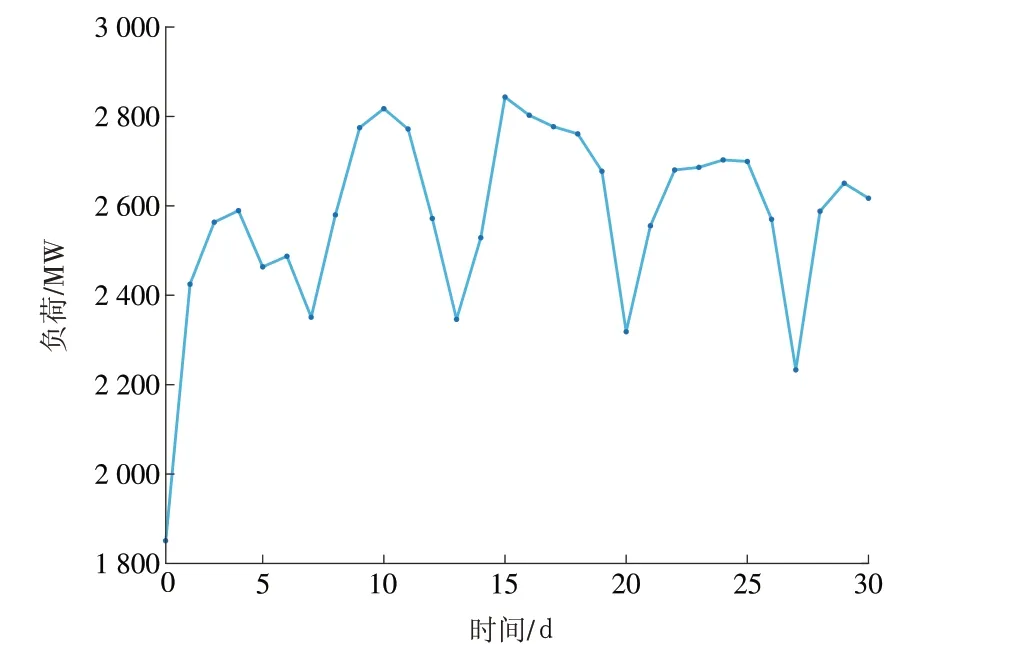
图5 月内负荷曲线Fig.5 Curve of the monthly load

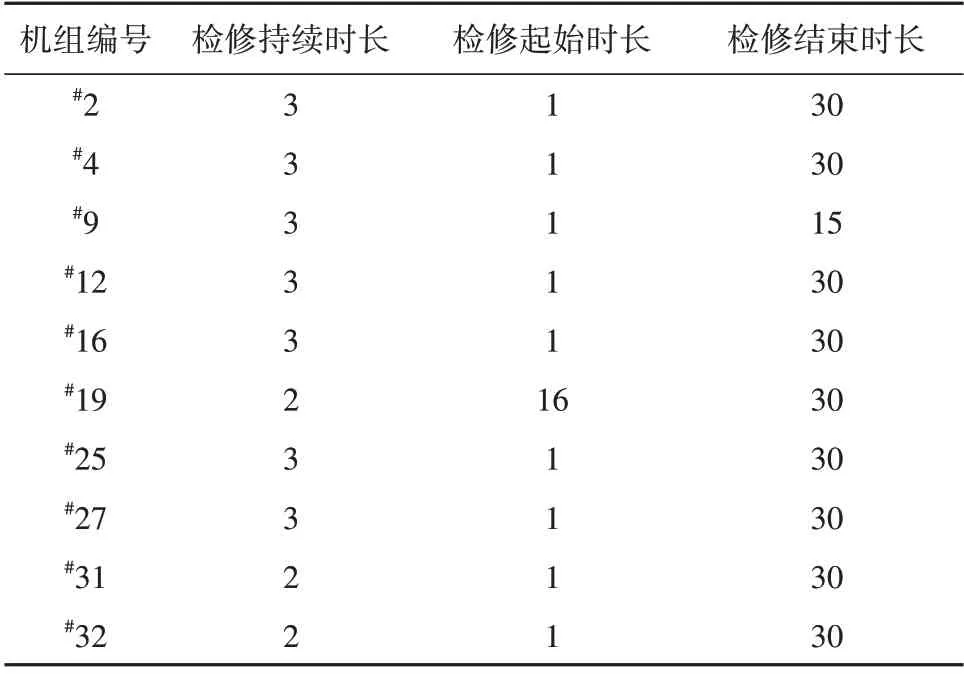
表1 部分待检修机组的检修区间Table 1 Maintenance interval of the units for being repaired d

4.2 改进算法与传统算法对比

为了能直观比较改进多目标量子行为粒子群算法和传统的多目标量子行为粒子群算法的优劣，本文引入Hypervolume 评价指标（以下简称HV 指标）。该评价指标最早由Zitzler等［24］提出，表示由帕累托解集中的个体与参考点在目标空间中所围成的超立方体的体积。基于HV 指标的评价方法可以直观地判断出算法得到的帕累托解集的优劣，即如果一个解集S 优于另一个解集S´，那么解集S 的HV指标会大于解集S´的HV指标。

接下来，将提出的基于深度强化学习的多目标量子行为粒子群算法与4种传统的多目标量子行为粒子群算法进行对比。其中，对于固定策略算法，取收缩-扩张固定系数为0.40。其他控制策略中，α1取0.60，α0取0.20。对于第2 章节中的模型，在IEEE-118 节点系统下采用上述5 种算法分别进行求解，并画出其HV指标值的变化，如图6所示。

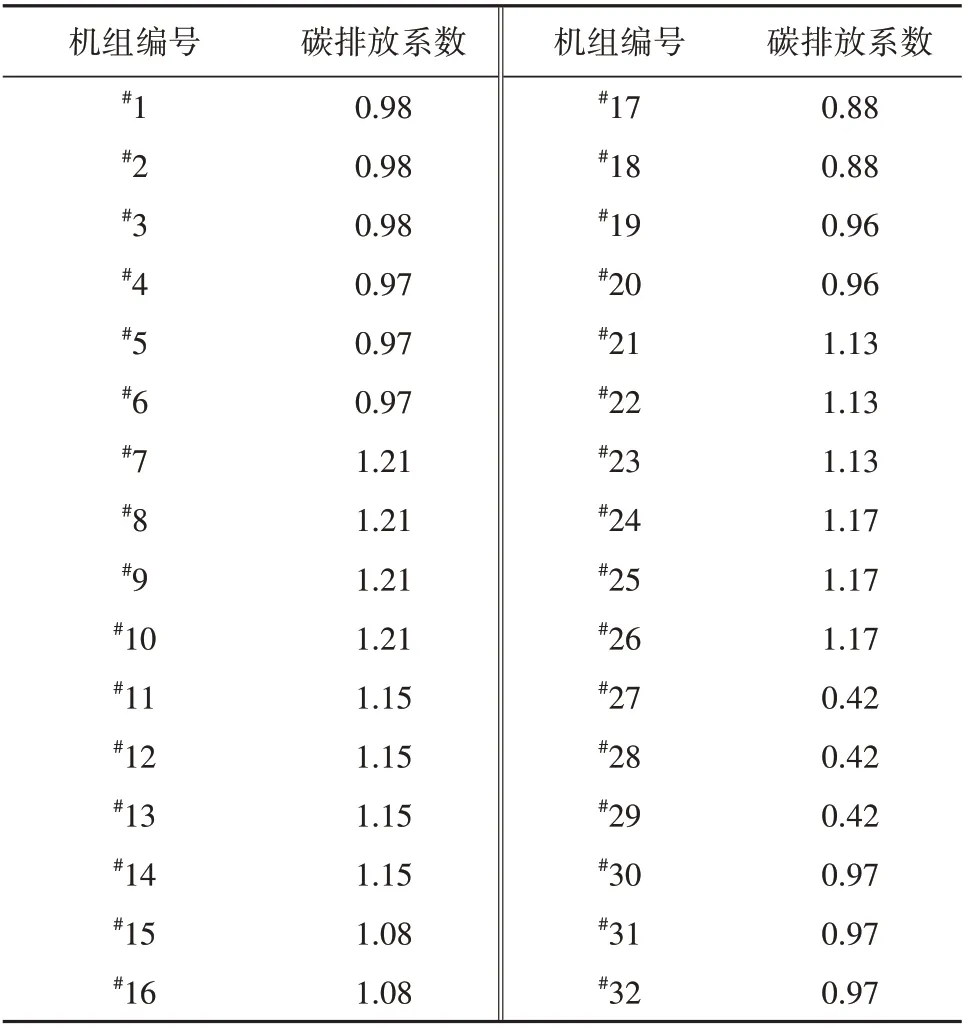
表2 机组的碳排放系数Table 2 Carbon emission factor of the units t/（MW·h）

从图6 中可以看出，基于深度强化学习的改进算法的HV指标值显然要比其他4种算法大，说明改进算法在求解多目标优化模型时比传统算法效果更好，可以获得质量更好的帕累托解集。因此，本文后续的多目标模型都将采用该改进算法进行求解。

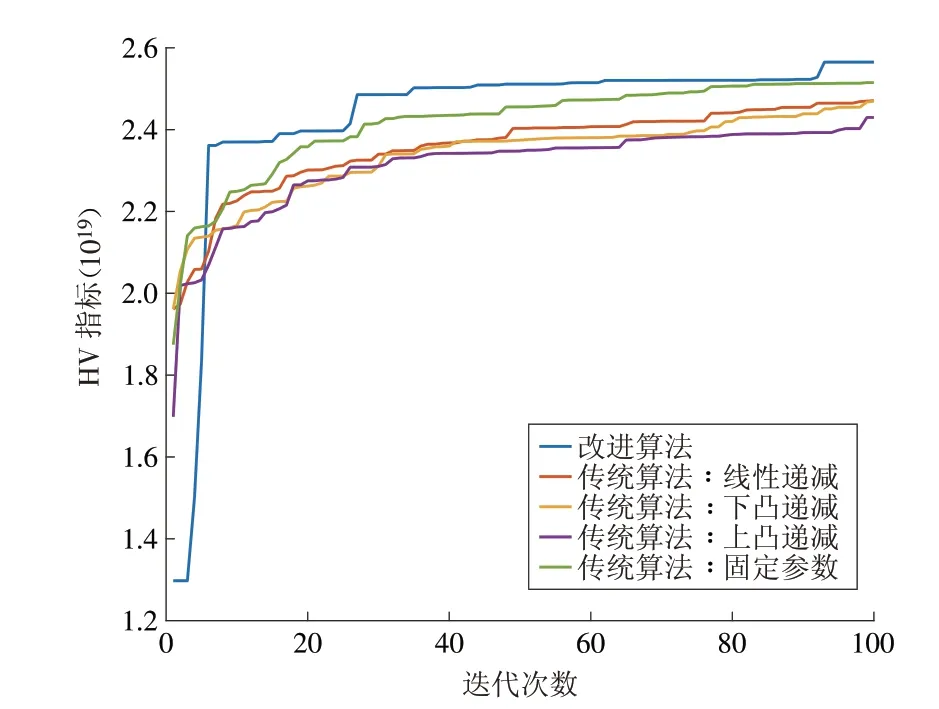
图6 改进算法与传统算法HV指标对比Fig.6 Comparison of HV indicator between the improved algorithm and the traditional algorithms

4.3 多目标优化模型仿真结果

在IEEE-118 节点系统下，采用提出的改进算法对第2 章节中的多目标模型进行求解，得到一组帕累托解。第1 章节中的模型包含2 个目标函数，为更加直观清晰地展示帕累托解集，分别画出每2个目标函数之间的帕累托曲线，如图7所示。由图7可以看出，求出的帕累托解集分布均匀，说明本文建立的多目标模型能兼顾多个指标，可以保障电力系统的经济性、安全性、环保性和稳定性。

图7 每2个目标函数之间的帕累托曲线Fig.7 Comparison of Pareto curve between different objective functions

本文采用改进的多目标量子行为粒子群算法求得了一组帕累托解集，而实际应用中往往只需要一个最终调度解。因此，还需要采用多目标决策综合评价方法从帕累托解集中选取一个满足多方面要求的最终调度解。

逼近理想解排序（Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS）方法由Hwang 等提出［25］，是一种常用的多目标决策综合评价方法。传统的TOPSIS 法采用欧氏距离来计算每个点到正理想点和负理想点之间的距离，但欧氏距离将不同属性之间的差别等同看待，有时不符合实际情况。而马氏距离不会受到各个变量之间相关性的干扰。因此，本文采用一种基于马氏距离改进的TOPSIS 法［26］从帕累托解集之中选取调度解。最终获得的调度计划见表3，机组出力如图8所示（由于篇幅原因，只随机选取部分机组展示其机组出力）。

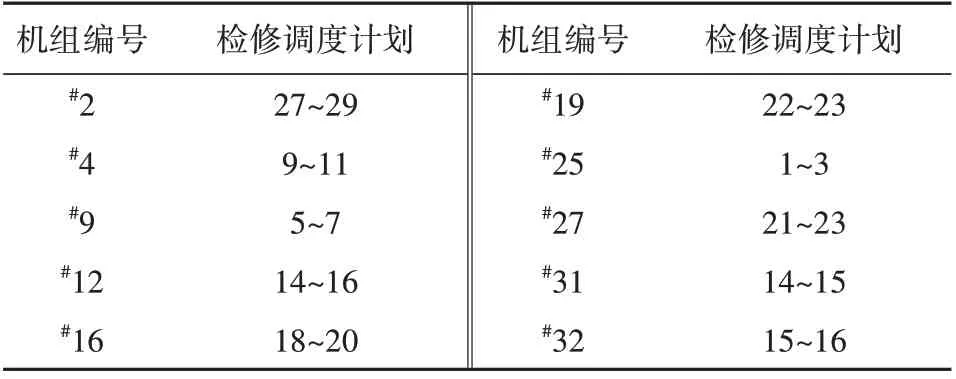
表3 部分检修调度计划Table 3 Maintenance and scheduling plan for units d

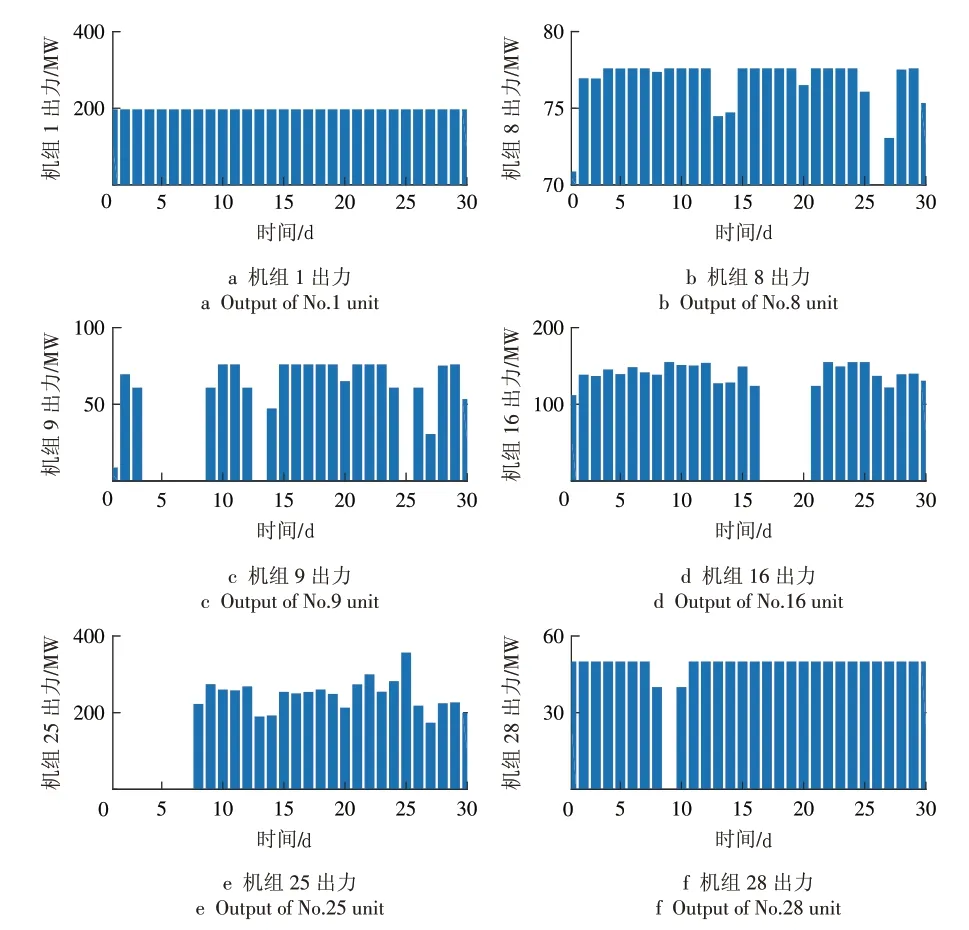
图8 部分机组出力Fig.8 Output of units

4.4 单目标与多目标优化模型仿真结果对比

在IEEE-118 节点系统下，2 个模型的5 个目标函数值见表4。由表4可知，多目标模型的优化结果在经济性目标和碳排放目标上都要比单目标模型略差一点，但是多目标模型调度结果的系统可靠性、节点电价稳定性和线路安全裕度都明显优于单目标模型结果。

表4 2个模型调度结果的目标函数Table 4 Objective functions for the scheduling results of two models

为更好地分析调度结果，绘制总成本目标和碳排放目标之间的关系，如图9 所示。该图表明，在IEEE-118节点系统案例中，帕累托解集中的碳排放目标函数值与总成本值大致成正相关关系。因此，单目标模型可以在求得最低的总成本的同时获得比多目标模型更低的系统碳排放量。

图9 多目标模型中2个目标函数关系Fig.9 Relationship between two objective functions in the multi-objective model

5 结论

本文构建了考虑碳交易的机组组合与检修多目标协同优化模型；同时，本文提出了一种改进的多目标量子行为粒子群优化算法来求解模型。在IEEE-118 节点系统下，首先，验证了改进算法的有效性；其次，发现多目标模型可以有效兼顾多个电力系统的指标；最后，将单目标模型与多目标模型的调度结果进行对比，发现多目标模型的系统可靠性、节点电价稳定性和线路安全裕度都明显优于单目标模型。