气力输送流型与压力信号关系研究

(华北水利水电大学 机械学院，河南 郑州 450045)

引言

流型又称为流态，是流体流动的形式和结构[1]。流型作为气力输送过程中的重要特征，直接影响气力输送的稳定性及机器的正常运行[2]。气力输送的稳定性关乎颗粒是否能够稳定、安全、可控地输出。

在气力输送过程中，由于受到气流场、颗粒之间及颗粒与管道的接触碰撞等因素影响，单个颗粒或者颗粒团均会呈现不同的运动状态。单个颗粒运动状态有悬浮、翻滚、旋转、下降、跳跃、滑动、碰撞等[3-4]；颗粒团则会出现颗粒均匀分布的悬浮流，上部悬浮而下部滑移的分层流，有时还出现上层颗粒悬浮而下层无滑移的沉积层流，满管状态的栓塞流和柱塞流等各种各样的运动流型。大量的实验表明在气力输送的过程中，颗粒在管道中流型并不单一，而是多种流型交替的出现[5]，并引起管内压力信号持续变化。压力信号的变化具有极大的随机性，但究其本质，取决于流体流动的状态，与管内的流型关系密切。

流型的准确识别受到诸多因素的影响，一直是一个复杂且难以解决的问题。王小鑫等[1]基于过程层析成像技术，对像素进行简单分析，利用二维最大熵阀值分割技术及遗传算法优化的神经网络分类器对重构的图像进行处理从而实现流型识别。高鹤明等[6]提出了一种基于阵列式静电传感器实现高压密相气-固两相流动状态识别流型的方法，利用静电传感器来感知具有敏感特性的流动带电微粒的流动状态，计算每个电极的熵，当电极的多尺度样本熵变化相似时，表明流动稳定，反之则流动不稳定。陈利东等[7]提出一种检测流型与判断稳定性的方法，通过分析和处理压力传感器采集的管内压力波动信号，发现不同流型的压力信号及功率谱的特征。

通过上述分析可知，压力信号可以作为流型判别的重要依据[8-9]。本研究从不同气力输送系统中取得了压力信号时域信息，通过提取压力信号的概率密度分布和功率谱分布特征，将其与高速摄像采集的流型对比，获得了管内不同流型与压力信号特征关联。

1 实验系统

1.1 实验装置及物料

实验装置由动力源组件葆德螺杆式空压机DHF-30PM、1 m3储气罐、凌宇LY-D 30AH干燥机，川祺0.35 m3仓泵给料组件、旋转阀给料组件、卸料除尘组件、采集控制系统和输送管道组成，如图1所示。在卸料器与旋转供料器之间布设亚克力透明管并采用高速摄像机NPX-GS6599UM获得物料输送流态图像信息；同时采用量程为0～1 MPa的压力传感器收集压力信号。

输送用的物料为黑色母粒，如图2所示。黑色母粒由高浓度炭黑和聚乙稀树脂高温密炼生成，外观呈直径为2.5 mm、高为3.5 mm的圆柱状，表面光滑亮泽和实色颜色稳定，韧性好，环保、无毒、无味、无烟，熔点在130～350 ℃，含水量0.001%。经测量，黑色母粒的真实密度为1.687 g/cm3，堆积密度为1.142 g/cm3。

1.2 实验过程

此次实验中有2个不同的输送线路，涉及两种类型的气力输送：当选择A线路时，输送系统为密相，物料从仓泵给料组件的料仓加入，被来自缓冲罐的空气流化后进入管道A，最终经旋风集料器到达料仓；当选择B线路时，输送系统为稀相，物料从旋转供料器上方的料仓加入，被空气携带经管道B至旋风集料器，最终被卸到料仓内。

2 流型划分及预测

2.1 流型划分

气力输送过程中，管内颗粒的流动状态是一个重要的特征参数，随着表观气速的变化，水平管内会出现各种各样的流型[10]：如图3a所示的悬浮流，该流型出现在表观气速较高的水平管内，为稀相输送，固体颗粒全部以悬浮的形式输送；如图3b所示的分层流，该流型由于重力的作用，颗粒在管道底部沉积，在管道上部的颗粒被高速气体携带，从而形成了上部稀相下部浓相的分层，上部颗粒高速向前而底部颗粒沿管道向前滑移；如图3c所示的沙丘流，该流型部分颗粒团聚在一起呈现栓状，管道顶部的颗粒团被高速气体吹散，呈现沙丘状沿管道前进，每一个沙丘之间存在分层流；如图3d所示的栓塞流，该流型栓塞与栓塞之间存在颗粒沉积层，颗粒充满整个管道并呈现清晰的前部边界和尾部边界特征，移动过程中，前部拾起颗粒尾部丢弃颗粒；如图3e所示的柱塞流，该流型出现在高固气比并且给料罐流化状态好的工况下，颗粒填满整个管道截面，并以柱塞状不断向前移动，此时表观气速较低[11]。

2.2 流型过渡的预测

文献[12]表明，雷诺数Re和阿基米德数Ar可用来描述颗粒运动的特征速度，两者呈幂指数关系：

Re=c·Arm

(1)

其中,c，m为常数，可通过实验获得；雷诺数Re和阿基米德数Ar计算方法如下：

(2)

(3)

式中,d—— 颗粒平均粒径

Ug—— 表观气速

ρg—— 气体密度

μ—— 气体黏度

g—— 重力加速度

ρp—— 颗粒密度

雷诺数Re和阿基米德数Ar能够较好的预测水平管流型的变化，在相同的阿基米德数Ar时，分层流和沙丘流的雷诺数Re比柱塞流和栓塞流的雷诺数Re大。因此，通过雷诺数和阿基米德数的关系可大致判断输送管道内的流型转换。

3 实验分析

3.1 参数分析

采用阿尔泰USB3100数据采集卡采集压力数据，根据奈奎斯特采样定理可知，为了防止颗粒流型特性的有效信息丢失，采样频率至少是最高信号频率的2倍，实际工程中一般取3～5倍。因此，采样频率为：

fs=5fmax

(4)

式中,fmax—— 压力信号中有效信息的最高频率

研究表明，气-固两相流的压力信号有效成分通常集中在10 Hz以下[12-15]，只有屈指可数的有效成分存在于10 Hz以上。为保证所有有效信号得到采集，实验设定采样频率为1000 Hz，满足实验需求，同时采用涡街流量计收集瞬时流量的变化，实验过程中两种系统的参数见表1。

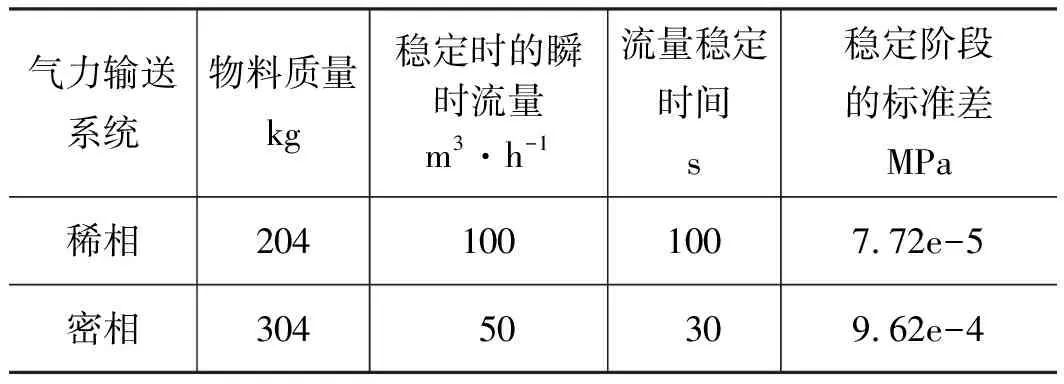
表1 两种系统实验参数Tab.1 Experimental parameters of two systems

稳定阶段的标准差计算公式[12]如下：

(5)

式中,pstd—— 压力信号稳定阶段的标准差

pi—— 压力信号

pm—— 压力信号的平均值

N—— 压力信号采集数

通过计算发现悬浮流的压力波动标准差数值为7.72e-5 MPa而沙丘流的压力波动标准差数值为9.62e-4 MPa。与悬浮流相比，沙丘流的数值大的多，原因是当管内为沙丘流时，颗粒的吹散与聚集导致管道实际横截面积不断发生变化，引起了实际气体流速的变化，从而导致压力信号p波动剧烈，使得其标准差较大。

3.2 流量分析

采用涡街流量计采集的数据绘制瞬时流量变化，如图4所示，其中Q1为稀相瞬时流量变化，Q2为密相瞬时流量变化。从图上可以得出，在输送的开始阶段，稀相的瞬时流量快速上升到220 m3/h，然后缓慢下降并维持在100 m3/h，表明稀相需要很大的气量将颗粒吹起，待颗粒在管道中悬浮后，流量逐渐稳定；而密相的瞬时流量先上升后下降，并稳定在50 m3/h。稀相输送过程持续了100 s而密相输送持续了50 s，密相气力输送系统在更短时间内输送了更多的物料，说明密相气力输送系统的输送能力远超稀相[16]。

3.3 压力信号波动处理

实验中收集的稳定阶段的压力信号难免受到各种噪声的影响，丛星亮[12]采用小波包技术分解压力信号，再通过自相关函数分析不同频段压力信号的时间相关性来判断该频段信号是否为噪声，得出了气力输送的压力信号波动的有效值主要集中在低频段6.5 Hz以下，噪声的信号主要集中在6.5 Hz之上。因此，将采集到的稳定阶段实验数据通过滤波器过滤(低通滤波器，截止频率10 Hz)，然后根据过滤后的实验数据绘制压力波动图，如图5所示。

从图5可以看出，稀相的压力信号波动范围为0～0.025 MPa，压力信号的脉动频率和幅度较小，曲线重复上升下降的过程；密相的压力信号波动范围为0～0.18 MPa，压力信号的脉动频率和幅度较大，曲线粗糙且不规律。上述现象产生的原因如下：当管内流型为悬浮流时，气速较高且稳定，颗粒可以悬浮并且稳定输送，当管内流型为沙丘流时，气速较低并且颗粒的聚集与吹散导致了管道实际截面的变化，引起了实际气体流速的变化，从而导致压力信号波动。因此相比悬浮流，沙丘流的压力信号波动更剧烈。

图6为高速摄像机所记录下的信息。从图6中可以发现，悬浮流的颗粒在管道内悬浮并且稳定向前移动，因此，认定其为稳定流型，压力信号波动平缓且平均幅度较小；而沙丘流前端不停拾起颗粒后端丢弃颗粒，管道实际横截面积变化频繁，为不稳定流型，压力信号波动剧烈且平均幅度较大，存在大量波动脉冲。

3.4 压力信号波动程度分析

为了更加直观的了解压力信号波动的程度，采用频数分布的方法对压力信号进行分析[17]，得到如图7所示的压力信号概率密度分布图，其横坐标是压力p，纵坐标是计数n，即压力重复出现的次数。

由图7可以得出，稀相的压力信号概率密度主要分布在0～0.0075 MPa，概率密度分布比较窄，呈现单峰分布；密相的压力信号概率密度主要分布在0.04～0.16 MPa，其概率密度分布较为分散，近似正态分布。上述现象说明：在气力输送过程中，物料流动越复杂，扰动越大，压力信号的概率密度分布越分散；物料流动越平稳，压力信号的概率密度分布越窄，呈现单峰状。因此，可以得出悬浮流的压力信号概率密度分布较窄，呈现单峰状；沙丘流的压力信号概率密度分布较宽，近似正态分布。

3.5 压力信号功率谱分析

功率谱密度(PSD)函数是快速傅里叶变换(FFT)的幅值的平方除以时间周期，定义了信号或者时间序列的功率如何随频率分布，其单边谱的功率谱密度(PSD)定义如下[12]：

(6)

单边谱密度函数中最大峰值定义为：

Pm=max(ρPSD(f))

(7)

研究表明，压力信号的功率谱密度函数的特征与管内流动状态紧密相连[18]。分析图5中的2组压力波动，做功率谱分析，得到不同流型的功率谱，如图8所示，横坐标为频率f，纵坐标为幅度Pa。

通过观察图8所示的功率谱密度，发现稀相的频率主要集中在0～0.5 Hz小频率区间，幅度最大值为250 MPa2/Hz，功率谱曲线存在一个很突出的峰；密相的频率分布较为分散，幅度最大值为180 MPa2/Hz，功率谱曲线呈现多峰状，在低、中、高频域皆有分布。上述现象说明：当功率谱呈现多峰状时，管内的流型相当不稳定，气力输送过程中发生了多尺度的脉动，压力信号变化频繁，此时管道内为沙丘流；当功率谱因表观气速增加，其多峰现象减弱呈单峰状时，管内的流型稳定，输送过程发生较为单一尺度的脉动，此时管内为悬浮流。因此可以得出，管内流动形式为悬浮流且压力波动幅度较小时，其频率主要集中在低频段；当管内流动形式为沙丘流且压力波动较大时，其频率在较宽的频域上分布。

通过上述分析可知，在气力输送稳定的情况下，水平管内不同的流型对应不同的功率谱函数图形，从而确定不同流型与功率谱函数图形的关系。

4 结论

本研究从不同气力输送系统中取得了压力信号时域信息，通过目标提取压力信号的概率密度分布和功率谱分布特征，并将其与高速摄像采集的流型对比，得到了管道不同流型与压力信号特征关联，结论如下：

(1) 通过计算压力信号波动的标准差，发现悬浮流的压力波动标准差数值为7.72e-5 MPa而沙丘流的压力波动标准差数值为9.62e-4 MPa，与悬浮流相比，沙丘流的数值大的多，原因是当管内为沙丘流时，颗粒的吹散与聚集导致管道实际横截面积不断发生变化，引起了实际气体流速的变化，从而导致压力信号波动剧烈，使得其标准差较大；

(2) 根据稳定阶段的数据绘制两种系统压力信号波动图，发现悬浮流的压力最大值为0.025 MPa，压力波动的范围在0～0.025 MPa之间且有规律，沙丘流的压力最大值为0.18 MPa，压力波动的范围在0～0.18 MPa之间并且压力信号曲线粗糙不规律；

(3) 通过对压力信号的概率密度进行分析，发现悬浮流的压力信号概率密度分布集中并且呈现单峰状；沙丘流的压力信号概率密度分布分散并且呈现正态分布状，因此沙丘流流动更加复杂；

(4) 通过分析两种工况的功率谱密度图，发现悬浮流的频率很集中且处于低频域，而沙丘流的频率分布分散且低，中，高频域皆有分布。