势问题维数分裂无单元Galerkin法影响因子的研究
2022-06-09李艳芳孟智娟李兴国任红萍
李艳芳,孟智娟,李兴国,任红萍
(太原科技大学 应用科学学院,太原 030024)
无网格方法[1]解决问题时,只需要节点信息,不需要划分网格,是有限元法后一种重要的方法。上个世纪70年代,Lucy等人第一次提出了光滑粒子法[2],并用这种方法研究了液体流动等问题,由于该方法不够稳定,故Lancaster等提出了移动最小二乘法(MLS法)[3-4],该方法求出的逼近函数具有较高的计算精度、光滑度也比较好,并在求解微分方程边值问题中得到应用。1992年,Nayroles等人根据MLS法,提出了扩散单元法[5-6]。在此之后,Belytschko等人在扩散单元法的基础上提出了无单元Galerkin方法(EFG)[7-8],接着解决了裂纹扩展和大变形等三维问题。张飞[9]对势问题用EFG方法和IEFG方法进行了对比研究。
后来,李东明等人建立了复变量无单元Galerkin方法(CVEFG)[10],并分析了弹性大变形问题。为了方便施加边界条件,任红萍等人提出了插值型EFG方法[11-12],并解决了波动方程等问题。但在用该方法解决三维问题时,计算效率比较低,会花费较长的计算时间,孟智娟提出了维数分裂无单元Galerkin方法[13],并将该方法应用于解决三维势问题、三维波动方程以及三维弹性力学等问题。
在DSEFG方法中,由于节点分布、dmax的取值会对计算精度和效率产生影响,因此本文对这些影响因子进行了研究,从而得出这些影响因子的最优取值。
1 三维势问题的分维过程
三维势问题的控制方程为:
(x=(x1,x2,x3)∈Ω)
(1)
本质边界条件为:
(2)
自热边界条件为:
(3)
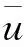
利用DSEFG方法求解问题(1)-(3)时,假设选取x3为分裂方向,将问题域Ω沿x3方向分裂为L层,间距为Δx3,即得到L+1个二维子域Ω(k),(k=0,1,…,L),则有:
(4)
这里
x3∈[a,c]
(5)
(6)
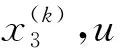
((x1,x2)∈Ω(k),x3=x3(k))
(7)
相应的边界条件为:
(8)
(9)
2 三维势问题的维数分裂无单元Ga-lerkin法
对问题(1)-(3),用DSEFG方法求解,即问题(7)-(9)用IEFG方法,x3上用有限差分法。
用罚函数法施加本质边界条件,得:
(10)
其中
(11)

(12)

Φ*(x(k))=
PT(x(k))A*(x(k))B(x(k)),
(13)
(14)
由方程(12)可得
(15)
(16)
这里
(17)
B(x(k))=(B1(x(k)),B2(x(k)),…,Bn(x(k))),
(18)
(19)
把式(12)、(15)、(16)代入(10)得:
(20)
讨论式(20)的各项积分为:
δuT·C·u″,
(21)
δuT·K·u,
(22)
(23)
(24)
δuT·Kα·u,
(25)
(26)
其中
(27)
(28)
(29)
(30)
(31)
(32)
将式(21)-式(26)代入式(20)得:
δuT·(Cu″-Ku+Kαu-F1-F2-Fα)=0.
(33)
由于δuT的任意性,可得:

(34)
其中:
(35)
F=F1+F2+Fα.
(36)

(37)
⋮
(38)
且有:
(39)
(40)
在x3上用有限差分法,得:
(k=1,2,…,L-1).
(41)
所以,方程组(34)表示为:
(42)
(43)
⋮
(44)
其矩阵形式为:
(45)
这里
(46)
令:
(47)
(48)
(49)
那么,方程组(45)可简化为:
EU=R.
(50)
(51)
3 数值算例
采用DSEFG方法求解三维势问题,分析了影响因子:节点分布、dmax对DSEFG方法精确度的影响。数值算例中,在每个积分单元上,用4×4点的Gauss积分。权函数采用三次样条函数,影响域为矩形域。
定义相对误差为:
(52)
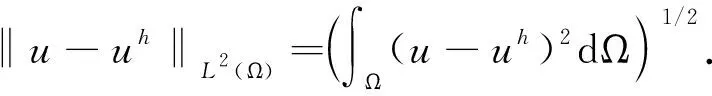
3.1 算例1
三维长方体内具有Dirichlet边界条件的Poisson方程
∇2u(x)=f(x),(x∈Ω)
(53)
(54)
边界条件为:
u(x)=0,(x∈Γ),
(55)
其中求解域Ω=[0,1]×[0,2]×[0,3].
对应的解析解为:
(56)
将求解域Ω沿x3方向均匀地分裂为L个子域,在平面Ox1x2上节点分布为9×21,即求解域Ω的节点分布为9×21×(L+1).
从图1可以看出,当L分别取21、17、12,且dmax=1.14,DSEFG方法的数值解都能较好的逼近解析解。图2中,求解域Ω的节点分布为9×21×17,当dmax不同时,数值解也能很好的与解析解切合。

图1 不同L时DSEFG方法的计算结果Fig.1 Calculation results of DSEFG method with different L

图2 不同dmax时DSEFG方法的计算结果Fig.2 Calculation results of DSEFG methods withdifferent dmax
表1和表2分别为L、dmax不同时DSEFG方法的相对误差与CPU时间,从表中可以看出,节点分布为9×21×17,dmax=1.14时相对误差最小,并且运行时间也较短。

表1 不同L时DSEFG方法的相对误差和CPU时间Tab.1 Relative error and CPU time of DSEFG method with disparate L

表2 不同dmax时DSEFG方法的相对误差和CPU时间Tab.2 Relative error and CPU time of DSEFG method with different dmax
图3显示了dmax=1.14时,L不同时DSEFG方法的相对误差,随着L的增大,数值结果的误差越来越小。图4是节点分布为9×21×17,DSEFG方法在dmax不同时的相对误差,可以得出dmax=1.14时得到的相对误差是最小的。

图3 相对误差随L的变化Fig.3 Varietion of relative error with L

图4 相对误差随dmax的变化Fig.4 Varietion of relative error with dmax
3.2 算例2
具有Neumann边界条件的三维立方体内的Laplace方程
∇2u(x)=0, (x∈Ω),
(57)
边界条件为:
(58)
(59)
(60)
(61)
其中求解域为Ω=[0,1]×[0,1]×[0,1].
对应的解析解是:
cos(πx3)cos(πx2).
(62)
将问题域沿x3作为分裂方向,均匀地分裂为10个子域,在平面Ox1x2上节点分布为M×M,即求解域Ω的节点分布为M×M×11.
表3和表4分别为M、dmax不同时,维数分裂无单元Galerkin方法的相对误差与CPU时间,综合两表,得出节点分布为11×11×11,dmax=1.15时相对误差最小,并且运行时间也较短。

表3 DSEFG方法的相对误差和CPU时间随M的变化Tab.3 The varietion of relative error and CPU time of DSEFG method with M

表4 DSEFG方法的相对误差和CPU时间随dmax的变化Tab.4 The varietion of relative error and CPU time of DSEFG method with dmax
图5、图6分别显示了不同节点分布和不同dmax时维数分裂无单元Galerkin方法的相对误差,其中将x3方向分裂为10个子域,从图中可以看出,节点分布为11×11×11,dmax=1.15时得出的相对误差是最小的。
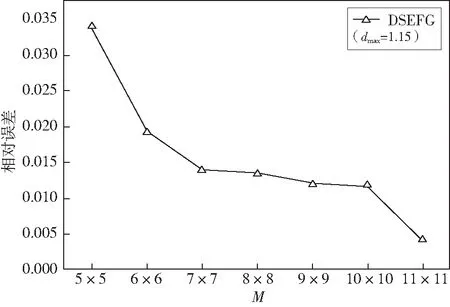
图5 相对误差随M的变化Fig.5 Variety of relative error with M

图6 相对误差随dmax的变化Fig.6 Varietion of relative error with dmax
4 结论
本文采用维数分裂无单元Galerkin方法求解三维问题,研究了在节点分布、dmax不同时,计算结果的精度和效率。在三维长方体内具有Dirichlet边界条件的Poisson问题中,选取节点分布为9×21×17,dmax=1.14时,计算精度最优;在具有Neumann边界条件的三维立方体内的Laplace问题中,取节点分布为11×11×11,dmax=1.15时,相对误差最小。
由算例可知,在给定了dmax下,随着节点个数的增加计算结果逐渐收敛;给定节点分布的情况下,随着dmax不断增大,相对误差并不是一直变大,而是在解析解附近波动。对于一般的偏微分方程,节点分布的多少与问题自身的定义域有关,定义域范围越大,划分的节点数相对越多。且dmax一般取大于1的值时,会得出更精确的结果。
