无限大板功能梯度材料裂纹尖端的应力场分析
2022-06-09张雪霞赵文彬
郭 璐,张雪霞,2,赵文彬
(1太原科技大学 应用科学学院,太原 030024;2晋中学院 数学系,山西 晋中 030619)
功能梯度材料是一种能够消除材料界面和脱层问题的特殊复合材料。由于FGM的非均匀性可以修复传统复合材料的缺陷,它在宇航、能源、电子交通、光学以及生物学等各个领域范畴应用广泛[1-2]。
毕贤顺[3]基于指数函数模型研究了FGM反平面作用下的Yoffe裂纹问题,得到应力强度因子表达式,并且研究了应变能密度因子对裂纹的影响。Vladimir[4]等人运用沿径向坐标变化的模型研究了材料非均匀性对功能梯度材料空心圆柱特性的影响。潘海珠[5-6]运用分段指数函数模型和积分变换法求解了FGM多裂纹断裂问题,并且讨论了不同弹性模量对断裂特征量的影响。Mohammad[7]等人运用应变梯度理论以及哈密顿原理研究了FGM厚度参数对梯度指数的影响。李涛、杨晓春[8]运用指数函数模型和拆分函数法对FGM的线裂纹的应力分布问题进行了研究。Zhang等人[9]运用数值积分法研究了无穷大FGM反平面静态裂纹和运动裂纹问题并且利用copson方法求解。近期,王素粉等人[10]利用有限元软件中参数计算法对功能梯度材料进行静态断裂力学分析,解决了一些因素可能导致的裂纹病态解问题。
在众多文献中,材料的物性参数变化都是用简单的指数函数模型表示,这样有利于问题的求解,但不符合材料参数的变化形式。本文充分利用了任意偶数次的负指数幂模型,运用数值解析法求解静态裂纹问题。
1 建立模型
如图1所示,假设在无限大板功能梯度材料中,有一条长为2a的裂纹。x轴和y轴相互垂直,假定材料的剪切模量按如下任意偶数次的负指数幂函数模型变化:

图1 含有限裂纹的功能梯度材料Fig.1 Functionally-graded material with finite-length crack
μx(y)=(μx)0/(c+α|y|)2k
μy(y)=(μy)0/(c+α|y|)2k
(1)
其中c>0,α>0,k>0,剪切模量为:(μx)0=μx(0)·c2k、(μy)0=μy(0)·c2k
应力-位移关系式为:

(2)
2 建立控制方程和边界条件
已知应力平衡方程:
(3)
将(2)式代入(3)式得到控制方程为:
(4)
给出无限大板FGM受剪切载荷作用的边界条件:
τyz(x0)=-τ0|x| (5.1) w(x,0)=0 |x|≥a (5.2) 根据裂纹的对称性,只需考虑在x>0,y>0的平面即可。引入关于x的Fourier余弦变换: (6) 将(6)式代入(4)式中得 其中 (7) 设变量代换 (8) 可推出 (9) 结合(7-9)式得到标准的修正Bessel微分方程: (10) 根据Bessel方程的通解形式并且考虑y→∞处的正则条件,方程(10)的解为: (11) 把(11)式代入到(6)式,得到: 把(11)式代入到(2)式,得到: (12) (13) 其中μy=(μy)0·c-2k 由(11)、(13)以及给出的边界条件(5.1)、(5.2)得到一组对偶积分方程组(14): (14) (15) 采用copson方法求解(14),得其解为: (16) 其中J0()是零阶第一类Bessel函数,函数φ(ξ)被如下第二类Fredholm积分方程控制: (17) 数值求解(17)式得到φ(1)的数值解。 对(16)式进行分部积分,得到(18)式: (18) (19) 考虑到s→∞处应力积分表达式,继而展开积分核较大的s值,并且考虑x→∞时,Kβ(x)和Kβ′(x)渐进性: (20) 定义复变量z1=x+iry,则有: (21) 这里的r1和θ1在图1中有定义。 第一类一阶Bessel函数需满足如下: (22) 由(19)-(22)得到如下(23.1)(23.2)式: (23.1) (23.2) 令x=r1cosθ1,y=r1sinθ1 公式(23.1)(23.2)在r1→0时,局部应力场如下: (24.1) (24.2) 由(23.2)、(24.1)得到应力强度因子的表达式: (25) 文章通过数值解析法将裂纹问题转化为第二类Fredholm积分方程,利用MATLAB对其求解,得到φ(1)的值。并且分析了相关参数与应力强度因子之间的关系。 如图2是取裂纹长度a=5,参数c=2,α=3在k=1,3,5,7时,表示无量纲应力强度因子与不均匀系数r和参数k之间的变化关系。 图2 不均匀系数r和梯度参数k对应力强度因子的影响Fig.2 The effect of inhomogenous coefficient r and gradient parameter k on stress intensity factor φ(1) 如图3是取k=3,r=1,α=2,在a=0.5,1.5,3时,表示无量纲应力强度因子与梯度参数c和裂纹长度a之间的关系。 结果说明:(1)从图2可以看出,给定a,c,α的值,当k一定时,r增大,φ(1)增大;当r一定时,k增大,φ(1)增大。由此可见不均匀系数r和梯度参数k与应力强度因子成正比例关系; (2)从图3可以看出,给定k,r,α的值,当a一定时,c增大,φ(1)减小;当c一定时,a增大,φ(1)增大。由此可见梯度参数c与应力强度因子成反比例关系以及裂纹长度a与应力强度因子成正比例关系。 图3 梯度参数c和裂纹长度a对应力强度因子的影响Fig.3 The effect of gradient parameter c and crack length a on stress intensity factor φ(1) 文章最终计算出的应力强度因子表达式以及数值实验结果与参考文献进行了比较。所得结果与文献[2]中的静态裂纹问题结果吻合较好。结果表明,在实际工作中可以通过控制材料的梯度参数以及裂纹的尺寸能够降低应力强度因子的值,进而防止由于裂纹的扩展造成的材料失效。3 导出对偶积分方程
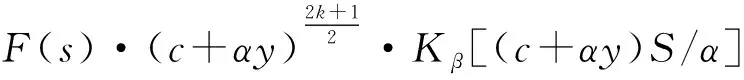
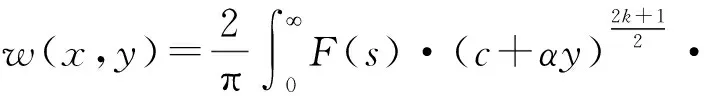
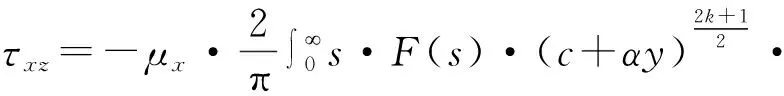

4 裂纹尖端处的应力强度因子
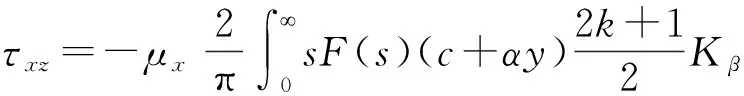


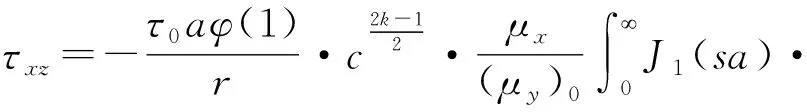

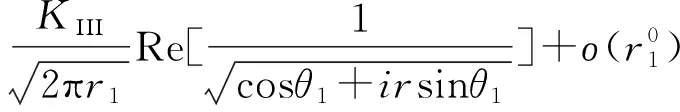

5 数值模拟

6 结论

