配合风电消纳的综合储能系统经济容量优化研究

郭琛良,张德虎,许 昌,薛飞飞

（1.河海大学 能源与电气学院，江苏 南京 210000；2.河海大学 水利水电学院，江苏 南京 210098）

0 引言

我国三北地区风资源丰富，风电装机容量大，但电网对风电消纳能力不足，出现了弃风限电问题[1]～[4]。为了解决弃风限电问题，北方地区逐渐部署风电供暖、储热装置混合供热，促进风电消纳，并出台了一系列政策鼓励新能源供暖[5]～[10]。

目前，通过热电联产机组消纳弃风进行供暖的相关研究有很多[11]～[14]。文献[15]建立了以热定电模式下不同热源运行的协调优化调度模型，在不同运行模式下得到了储热低压装置切除方案，燃料利用程度和灵活性最优。文献[16]针对风电消纳建立了热电联产机组和风电机组的联合运行模型，基于模拟退火粒子群算法求解模型，采用负荷侧峰谷电价策略和储热的联合优化调度方法，可使系统综合效益最高。文献[17]研究电锅炉与储热装置联合运行调度策略，建立了电锅炉与储热装置联合调度的风电消纳经济与环保调度模型，电锅炉运行在最小启动电功率时，系统经济与环境效益最优。上述文献对电锅炉和储热系统联合供暖提出了控制策略和经济优化分析方法，储能系统的经济容量优化配置方法需要兼顾经济效益和风电消纳效果。

氢能是“环境友好型”能源载体，电能-氢能的循环实现了能量流动，串联电-气能源网带动绿色无污染能源消费。氢热电储能系统的经济优化配置方法已有相关研究，文献[18]建立了包含氢储能和电池储能的风-光-储微网优化模型，综合考虑环境效益和经济效益，结果表明，优化的储能容量配置可以减少能源浪费，并增加经济效益。文献[19]针对含风电和水电等可再生能源和储氢综合电力系统氢储能容量配置，建立了以风电上网电量最大和水电经济效益最大为目标的氢储能系统容量配置优化模型，结果表明，氢储能系统能达成目标。上述文献分析了包含氢储能的储能系统去确定容量方法，但目前还没有对含氢热电综合储能系统的优化定容方法的研究。

本文针对风电消纳的综合储能系统提升经济性的容量配置方法，在现有储热储电研究的基础上加入储氢进一步消纳风电，并建立综合储能系统配备容量的多目标函数模糊优化模型。上层模型对综合储能系统成本和运行效益进行分析，以经济性最优为目标，包含政策补贴对风电消纳的影响，对综合储能系统经济性进行分析时分别考虑环境补贴和调峰补贴；下层模型分析综合储能系统功率分配，因为储能电池和储热装置在充放电过程中都有能量损失，会间接影响储能系统装置使用寿命和经济效益，所以下层模型以电池功率循环和储热罐热量循环次数最小为目标，以保持设备健康的运行状态和减少系统能量损失。上下层目标函数按照相应的隶属度函数进行满意度计算，综合上下层模型的满意度，求出效益优化的容量配置。

1 储氢热电综合储能系统基本结构

本文综合储能系统（Energy Storage System，ESS）的地区范围性供热结构如图1所示。ESS有氢储能、电储能、电锅炉和储热装置等。

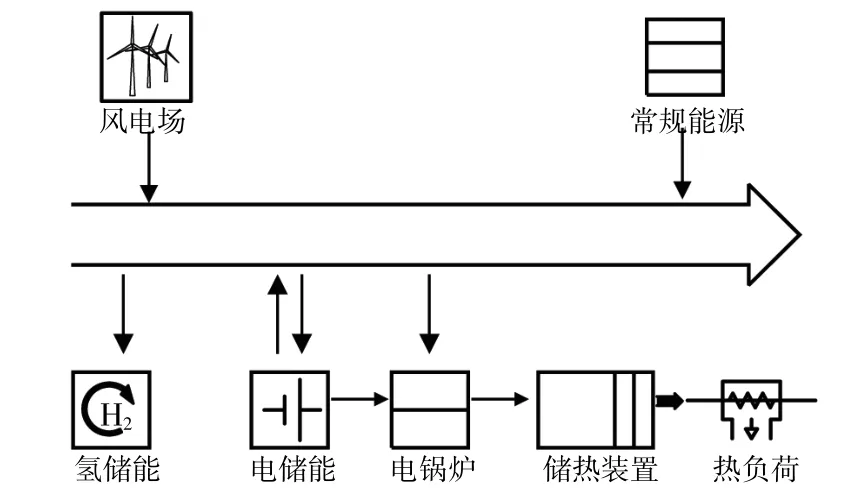
图1 综合储能系统结构Fig.1 Structure of ESS

2 综合储能系统的经济性容量配置双层优化模型

双层优化模型结构如图2所示。

图2 容量优化模型结构Fig.2 Structure diagram of capacity optimizationmodel

综合储能系统的经济性容量配置双层优化模型中，上层模型考虑综合储能系统的经济效益最优，综合考虑储能系统的环保收益、减排收益、制氢收益和居民供热收益等成本分析；下层模型考虑优化综合储能系统中的电力循环和热力循环，通过减少能量在储能系统中的循环量以减少循环过程中的能量损耗。上下层优化结果以模糊隶属度进行量纲上的统一并求出折中最优解。0满意度意为完全不接受目标函数值，而1满意度意为完全接受目标函数值，0～1满意度意为对目标函数值的部分满意。优化模型的分层模糊隶属度u1，u2，满意度标准值μ分别为

式中：f1，f1max，f1min分别为上层目标函数值及其最大、最小值；f2，f2max，f2min分别为下层目标函数值及其最大、最小值。

2.1 模型目标函数

双层模型目标函数分别为综合储能系统运行收益最优和储热装置与储能电池功率分配优化，即上层目标函数f1为经济收益最大，下层目标函数f2为储能装置循环次数最小。

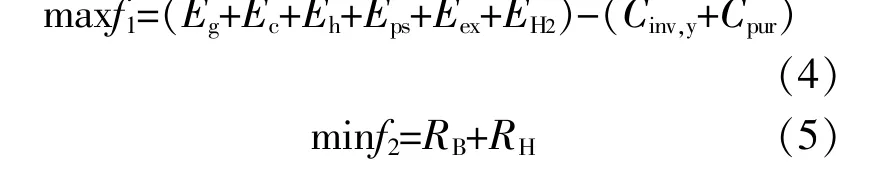
式中：Eg为综合储能系统的环保收入；Ec为节煤减排收入；Eh为供暖收入；Eps为调峰电量收入；Eex为电价交换收入；EH2为制氢收入；Cinv，y为系统投资年值；Cpur为综合储能系统购电成本；RB为储电装置电量循环次数；RH为储热装置热量循环次数[20]。

①年化投资成本

年化投资成本包括两部分，分别为购买成套设备成本与运营维保费用，其中购买成套设备成本包括氢储能，电池储能与热储能的设备成本。

该中央空调器为36个房间提供服务，其中有20个双人靠舷侧外舱，并有16个四人内舱。根据热负荷计算：双人外舱因有较大的飘窗，每个舱室的热负荷为1 100 W；四人内舱每个舱室的热负荷为400 W。

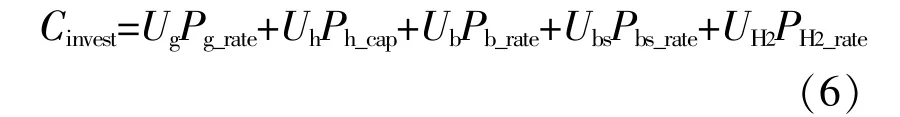
式中：Cinvest为设备投资成本；Ug为电锅炉成套设备成本；Pg_rate为电锅炉的标定容量；Uh为单位储热成套设备建设成本；Ph_cap为储热成套设备的标定容量；Ub为单位电池储能成套设备成本；Pb_rate为电池储能功率的标定容量；Ubs为单位电池储能容量的成套设备成本；Pbs_rate为电池储能成套设备的建设容量；UH2为氢储能单位容量的成套设备成本；PH2_rate为氢储能成套设备标定功率[20]。

设备的年化运营和维保成本可表示为设备投资建设成本总值乘以年化运营和维护费率，运营和维护费率为2%。

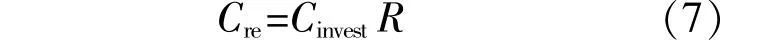
式中：Cre为年化运营和维保成本；R为年化运营和维护费率。

年化投资成本包括成套设备投资成本年值与年化运营和维保成本。

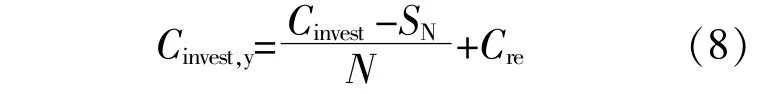
式中：SN为设备报废售价；N为设备使用寿命。

②储电充放电次数

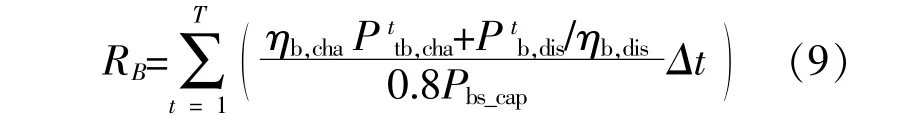
③储热装置储放热次数

2.2 模型约束条件

①电能平衡约束

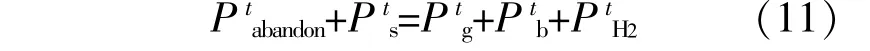
②热平衡约束

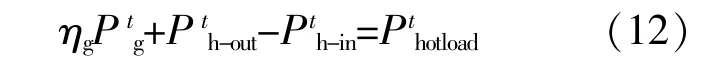
3 氢热电混合储能系统的经济性评价指标

本文以氢热电综合储能系统的投资回收期，评价所提出的双层优化配置结果下供暖方式的经济效益，其数学模型为

式中：Y为投资回收期，电池储能和氢气储能设备的使用寿命均为20 a，所以综合储能系统的设计全寿命周期为20 a，投资回收期越低，资本回收越快，盈利越多，综合储能系统的投资经济效益越可靠。

模型未考虑氢储能和电储能在非供暖期的收益情况，全年的制氢收益会使综合储能系统年净收益提高，投资回收期将缩短[20]。

4 模型求解

由于风电的不确定性，不同的储热式电锅炉的容量配置与电池储能的容量配置在不同的弃风场景下，会产生不同的运行效果，同时二者之间不同的容量比例关系也会影响系统的弃风消纳效果以及蓄热罐与电池储能的使用程度，故采用典型日数据还是场景削减的方法都很难准确地确定混合储能系统中各装置的最佳容量配置[20]。因此，本文的储能系统定容方法，无法通过普遍典型日数据等确定风电场储能系统的容量。但是可以依据当地供暖期热负荷数据和风电出力数据。本文所提方法可适用于确定类似的配合风电消纳的储能系统容量配置。

本文模型中所使用的风电机组相关参数如表1所示。

表1 风电机组相关参数Table 1 Relevant parameters of the wind turbine unit

由于弃风的不确定性，利用全供暖期的实际风电场的弃风数据以及供热数据，采用10min为一时段。以运营收入最大和成本支出最小为目标求出上层目标函数，以热量循环和电能循环次数最小为目标求出下层目标函数，经过多次循环，最后求得最大满意程度的模型优化结果，作为储能系统的定容结果。模型求解的流程如图3所示。

图3 优化方案结构Fig.3 Structure chartof optimization scheme

5 计算分析

5.1 算例数据

以北方某风电场2018年运行数据进行模型计算分析，风电场总装机容量为30 MW。整个供暖期（10月末-3月初）计算139 d，其中约有20 000个弃风区间（10min为1区间），弃风总量约为9 249.2MW·h，区间平均弃风功率为2.77 MW。期间供热负荷总需求为6 043.3MW·h，10 min平均供暖热负荷功率为1.81MW，其中日平均供热需求负荷为43.48MW·h。弃风功率曲线和供热需求负荷曲线如图4，5所示，分时电价见如表2所示。

图4 弃风功率Fig.4Wind curtailment power

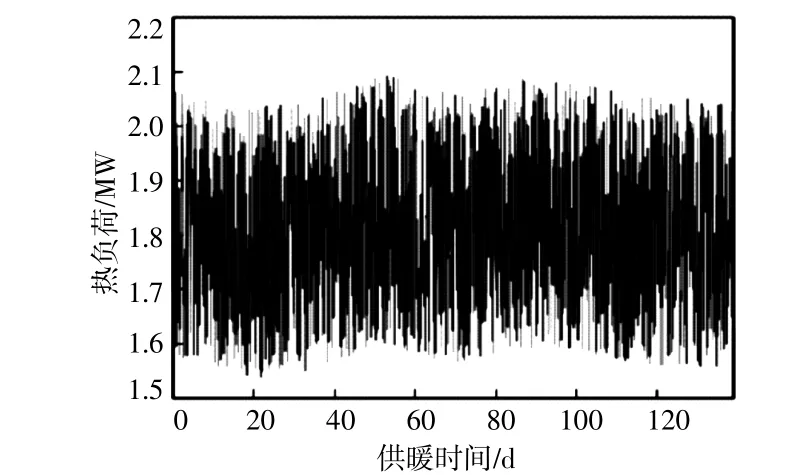
图5 热负荷Fig.5 Thermal load

表2 某地分时电价Table 2 Local time-sharing tariff

由图4，5可知，弃风功率平均值大于2.5 MW，而热负荷为2.1～1.5MW。可见通过配置足够容量的综合储能系统，弃风功率可以满足热负荷需求，而满足热负荷之外的弃风电量可用来制氢。

如果储能电池在负荷高峰时能保证供暖需求之外还有剩余的电量状态，将会向电网售电获得电价交换收益；如果储能电池在负荷低谷吸收弃风电量后还有状态余量（State ofCharge）可以充电，将会从电网购电，以获得峰谷交换电量收益。在计算储能电池和储氢装置的设备建设成本时，要考虑到20 a投资回收期中进行换新成本。

5.2 优化定容结果

目前，各省政策补贴分为3种情况：①仅环境保护补贴；②仅调节峰谷电补贴；③环境保护补贴和调节峰谷电补贴。本文通过投资回收期指标来比较分析3种情况下的容量配置结果。容量优化配置如表3所示。由表3可以看出，仅考虑环境补贴和调峰补贴情况下的电锅炉储热和电池储能的容量优化配置都小于环境补贴加调峰补贴情况，表明在环境补贴加调峰补贴的情况下，储能系统可以消纳更多弃风和进行调峰；而仅考虑环境补贴或调峰补贴情况，则会减少储能系统的补贴收益，减小容量配置，进而减少储能系统的弃风消纳能力本系统环境收益占不到全部收益的10%，对综合储能系统经济收益的影响较小；而调峰收益占全部收益的20%左右，对综合储能系统经济收益影响比环境收益更大。在3种补贴方式中，容量配置最高的是环境补贴加调峰补贴，容量配置最低的是环境补贴，调峰补贴的容量配置介于两者之间。仅调峰补贴与环境补贴加调峰补贴相比，容量配置比较接近，这是因为调峰收益比环境收益大，环境收益几乎没有影响储能系统容量经济优化配置。

表3 容量优化配置Table 3 Capacity optimization

5.3 容量优化配置结果分析

容量配置结果如表4所示。由表4可知：3种补贴方式下，环境补贴加调峰补贴带来的年收益最高；仅考虑环境补贴时，年收益最低；仅考虑调峰补贴时，年收益介于前两者之间。弃风消纳的结果也是环境补贴加调峰补贴最高，仅环境收益最低。环境补贴加调峰补贴条件年收益最高为654.45万元，仅环境补贴条件年收益最低535.10万元，资本投资回收期在20 a内，能够在投资回收之后实现盈利。按照供暖期总的弃风电量9 249.2MW·h，3种补贴方式下，仅环境补贴情形弃风消纳量最低为6 818.1 MW·h，环境补贴加调峰补贴条件弃风消纳量最高为6 851.3 MW·h，综合储能系统至少消纳73.72%的弃风，消纳弃风表现良好。减排方面，也是环境补贴加调峰补贴最高，仅考虑环境收益时最低。这是在环境补贴加调峰补贴的情况下，综合储能系统可以配置更多容量来消纳弃风，减少碳排放。制氢消耗的弃风电量在环境补贴下为143.59 MW·h，在环境补贴加调峰补贴时为142.69 MW·h，二者相差不大，表明氢储能已经充分发挥了消纳风电的能力。

表4 不同容量配置下的供暖期运行结果Table 4 Operation resultunder different capacity configuration in heating period

5.4 储能系统的容量配置结果分析

根据前文提出的储能系统的经济性评价指标，对不同补贴的储能系统经济性提出评价。本文从考虑调峰收益加环境收益情况和仅考虑调峰收益对储能系统经济性进行评价，如图6所示。

图6 投资回收周期Fig.6 Investment recovery cycle

由图6可以看出：环境补贴加调峰补贴的情况下，投资回收周期最短为14 a，仅考虑调峰补贴的情况下约为17 a；仅调峰补贴比环境补贴加调峰补贴的投资回收期稍短，表明环境补贴带来的额外收益使得综合储能系统配置更多的储热电容量，储热装置对于热量的储存和储能电池对于弃风电量的储存使得储能系统能够消纳更多弃风电量并得到收益。

5.5 氢储能建设成本和电池成本对经济性的影响

氢储能站和电池是综合储能系统建设主要成本。氢储能消纳弃风和增加新能源渗透率，但其建设成本过高且氢气储运成本也比较高。将氢储能建设成本和电池建设成本分别压缩至90%，80%，70%，60%和50%进行分析，如图7所示。随着储氢装置成本的下降，综合储能系统的投资回收期显著下降，净收益出现了显著上升，表明储氢装置成本在投资建设成本中占比很高，储氢建设成本的降低能够很大程度上提高系统的经济性。随着电池成本的下降，综合储能系统的投资回收期小幅下降，净收益出现小幅上升，提高了系统的经济性。

6 结论

本文通过容量优化模型，分析了储能系统的经济性，得到以下结论：①多种储能方式相结合，尤其是储氢装置的加入可以大幅提高综合储能系统的弃风消纳能力和经济效益，提高电力系统灵活性。结果表明，本文综合储能系统的经济性定容方法可以消纳70%的弃风，综合储能系统的环境收益与节煤收益提高约20%，投资回收期约15 a，证明了储能系统经济最优配置方法的合理性；②考虑综合储能系统的不同形式的补贴，在高补贴的情况下综合储能系统消纳和减排效果更好。综合储能系统的经济效益不仅受外在政策补贴的影响，也会受到自身成本控制的影响。储氢装置和储能电池建设成本的下降能够显著提高综合储能系统的弃风消纳能力和经济效益，减少投资回收期。