基于数学方法的音乐流派影响因素与演变预测研究

李 梦，张 枫，李 勇

基于数学方法的音乐流派影响因素与演变预测研究

李 梦1，张 枫1，李 勇2

（1.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030；2.安徽财经大学 经济学院，安徽 蚌埠 233030）

音乐作为人类文化遗传的一部分，与人类的生活密不可分。同时，不同的音乐流派也对人类的社会生活有不同影响，研究音乐流派发展就显得十分必要。首先利用灰色关联分析与K-Mean聚类分析对影响音乐流派的因素进行了分析，然后基于已有数据，建立了时间序列ARMA模型，对音乐流派在未来5年的发展趋势进行了预测。

灰色关联度分析；K-Means聚类分析；ARIMA时间序列分析；Python；MATLAB

音乐是人类社会文化遗产的重要组成部分。当艺术家创作一首新音乐时，有许多因素会影响他们，包括自身的创造力、社会环境、所使用乐器，或其他个人经历。研究革命性变化、新的流派以及艺术家的合作等对音乐的影响力产生影响，捕捉音乐艺术家之间的相互影响，能够更好了解随着时间的推移，音乐影响力的发展与演变。

本文通过建立数学模型，对影响流派内艺术家与流派间艺术家的相似性与差异性的关键因素进行研究，并在此基础上对未来音乐流派走向进行趋势预测。利用2021年美国大学生数学建模竞赛D题中所提供的数据集，首先用灰色关联分析与K-Means聚类分析，得出流派内与流派外不同艺术家之间的相关关系，并得出流派相似与差异的关键影响因素；然后利用已有数据，建立ARMA时间序列模型，预测得出未来的音乐流派走势。

1 音乐流派的相似性分析

1.1 研究思路

已知完整的汇总数据集，制定音乐相似性的度量标准，建立数学模型来比较流派内的艺术家与流派间的艺术家间的相似性。首先，对数据进行预处理后通过相关性分析探究各指标间的相关关系，根据皮尔逊相关系数可以得出指标间的相关性，剔除相关性较低的指标，得到音乐相似性度量。然后采用这些指标，通过灰色关联度分析得出音乐间的相似程度。在此衡量标准上，根据艺术家所属流派，对于艺术家进行K-Means聚类分析，分别得出流派内与流派间的艺术家的相关关系，聚类分析图可以直观反映流派间与流派内的关系，据此比较得出流派中的艺术家是否比流派间的艺术家更相似，进一步得出各流派的区别。

1.2 理论基础

(1)灰色关联分析法原理：灰色关联度分析是一种分析系统中各因素关联性程度的方法，由关联系数得到关联度，按关联度大小进行排序、分析得出结论。灰色关联分析的步骤一般为：

①确定参考列和比较列。参考列用于反映系统的行为特征，比较列是由能够影响系统行为的因素组成。

②数列的无量纲化，由于各因素计量单位不同，难以比较，所以，在计算关联度之前，需要完成无量纲化处理，把指标实际值转化为指标评估值，将它们统一到近似的范围内，重点关注其变化和趋势。

③关联系数计算。可以用曲线间的差别程度来测算它们的关联度。针对一个参考数列，存在多个比较数列，计算每个比较数列与参考数列对应元素在各时刻的差值也就是关联系数，公式如下：

式中：是分辨系数，一般在0～1之间，通常取0.5；min表示两级最小差，max表示两级最大差；各比较数列X曲线上的每个点与参考数列0曲线上的每个点的绝对差值记为0i()。

④关联度计算。每个比较数列和参考数列的关联程度是通过多个关联系数来反映的，信息分散，因此很难从整体上比较，需要用一个集中值取代每个时刻的关联系数。各时期关联系数的均值常被用作这个集中值，公式如下：

式中：是选取的时刻即曲线中的点的个数；r值越接近1，说明相关性越好[1]。

(2)K-Means聚类分析原理：K-means算法是最常用的一种聚类算法。通过该算法可以将样本进行聚类，具有相似特征的样本聚为一类。

①选定需要的类别数目，作为聚类中心点。

②计算每个样本点与聚类中心的距离并分类，将样本点归到最近的中心所在的类，一次聚类完成。K-means算法的类簇中心由如下公式计算得出：

式中：C表示第一个聚类的中心，-1≤≤，|S|表示第一个类簇中对象的个数，X表示第一个类簇中第各对象-1≤≤|S|。

③比较样本点的类别情况在聚类前后是否保持不变，不变的情况下算法终止，如果发生变化则进行第四步。

④计算聚类前后类别情况保持不变的样本点的中心点，作为该类的新中心点，返回第二步进行。

2.4.5 不同文化程度的医务人员院感知识认知正确率比较分析 比较分析不同文化程度医务人员院感知识认知正确率发现差异有统计学意义（P＜0.05），随着文化程度的提高，医务人员院感知识认知正确率逐渐增高，见表4。

1.3 研究过程及结果

首先利用数据集中的指标画出热力图对相关性进行分析，见图1。

图1 热力图

从图1中可以看到，popularity与year之间的皮尔逊相关系数是所有指标间最大的，loudness与energy，acousticness与popularity，acousticness与year间也具有较强的相关性，其他指标间的相关性较低予以剔除，采用上述指标作为音乐间的相似性度量。以前7首歌曲为例，根据相似性度量数据，采用灰色关联分析法可以计算得出这7首音乐间的相似程度[2-4]，见表1。

表1 音乐间相似程度表

0123456 01.0000000.9881850.8763540.7619150.8714310.6617390.698345 10.9884241.0000000.8803490.7603370.8739610.6651950.698032 20.8863680.8881721.0000000.8595680.7627000.6637570.744161 30.8140310.8109340.8804241.0000000.8011690.6747760.784102 40.9028120.9042220.8248990.8196061.0000000.7472700.726370 50.7496620.7494050.7376450.6863610.7342481.0000000.758260 60.6983450.6949630.7297780.7177220.6358550.6909941.000000

将音乐流派作为横坐标，将上述3个指标分别两两为一组作为纵坐标和竖坐标，对所有艺术家进行K-Means聚类分析，以genre-loudness-energy为例绘制出三维分布图，如图2所示。

图2 genre-loudness-energy聚类三维分布图

图2表明流派不同（横坐标不同）的艺术家间可能相似也可能不相似，但即使是同一流派（横坐标相同）也有很大程度可能不相似。同理对其他几组数据进行分析，可以得出流派中的艺术家不一定比流派间的艺术家更相似的结果。

通过对单个流派的相关性分析（以Country为例）得出流派间和流派内部具有一定的影响，主要体现在popularity、year、loudness、energy、acousticness这5个指标上，其中popularity与year的影响最强。针对4组指标分别绘制出聚类三维图。

根据图3可知：流派间的相似之处主要在于loudness和popularity，流派内部的相似之处主要在于loudness，一定程度在popularity上相似。流派的区别主要在于energy、acousticness和year这3个指标上[5-7]。

2 音乐流派走向预测

2.1 研究思路

已知时间推移的前提条件，比较流派之间和流派内部的相似性和影响。将各流派的指标画出随时间推移的折线图，可以直观看出流派随时间推移的变化。在此基础上，进一步进行时间序列分析，预测流派未来的变化趋势。结合上述分析，对数据集进行分类汇总，可以得出有些流派是否与其他流派有关联。

2.2 理论基础

常用时间序列模型有自回归模型、移动平均模型、自回归移动平均模型和自回归求和移动平均模型等。平稳时间序列主要通过这些模型进行拟合，非平稳时间序列则需依靠差分运算转化为平稳时间序列，然后再选择模型进行拟合[8]。自回归移动平均模型(ARMA(p,q))是时间序列中最为重要的模型之一，多应用于观测值超过50个的情况，主要由AR、MA两部分组成：AR代表p阶自回归过程，MA代表q阶移动平均过程，其公式为：

依据模型的形式、特性及自相关和偏自相关函数的特征，总结如下：

表2 时间序列模型特征总结

AR(p)MA(q)ARMA(p,q) 模型方程φ(B)Zt=atZt=θ(B)atφ(B)Zt=θ(B)at 平稳性条件φ(B) =0的根在单位圆外—φ(B)=0的根在单位圆外 可逆性条件—θ(B)=0的根在单位圆外θ(B)=0的根在单位圆外 自相关函数拖尾q步结尾拖尾 偏自相关函数p步结尾拖尾拖尾

2.3 研究过程及结果

选取Country流派为例，以时间为横坐标，各指标为纵坐标，绘制出簇状图，见图4。从图4中可以看到，该流派的流行度在未来的5年中将会继续增加。

以energy指标为例，绘制数据的时序图和自相关图，进行序列的平稳性检测，见图5，结合图5可得，原始序列的ADF检验结果为：

(-1.2276, 0.66162,2,78,

{'1%':-3.517113604831504,

'5%':-2.8994,'10%':-2.5869},-221.6748)

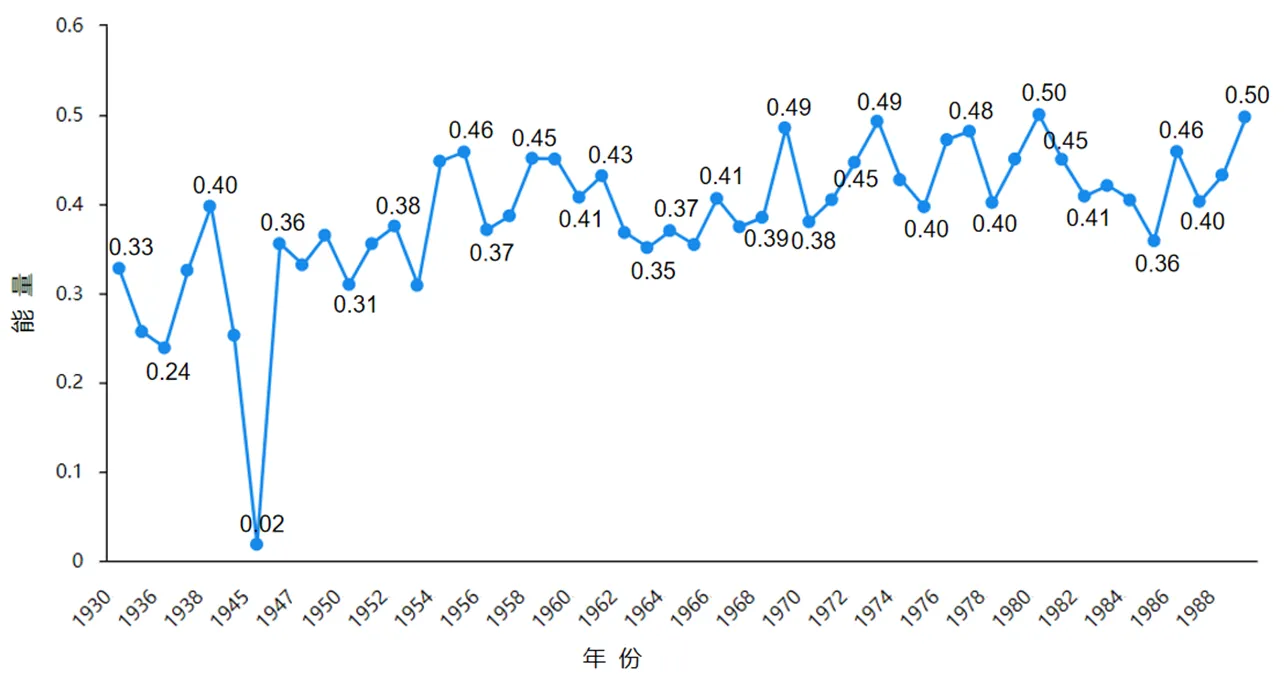
图4 Country流派指标簇状图

时序图显示该序列呈显著的递增趋势，可以判断该序列是非平稳序列；自相关图显示自相关系数长期大于零，说明序列间的长期相关性很强；单位根检验统计量对应的值为0.6616，显著大于0.05，可以判定该序列是非平稳序列。

将序列一阶差分并进行ADF检验，得出一阶差分后的序列是平稳序列。对模型进行定阶：BIC最小的值和值为：0、1，模型定阶完成。最后采用AR(1)模型进行拟合，即对原始序列建立ARIMA(1,1,0)模型[9-11]。

图6 时间序列模型报告

作出向后5期的预测，返回预测结果、标准误差、置信区间。得出随着时间推移向后5期的预测值为：0.710 847 9，0.716 214 19，0.721 580 48， 0.726 946 78，0.732 313 07，符合簇状图的稳步上升趋势。其他指标预测处理同上。

2.4 检验

序列的白噪声检验：所建模型的残差序列为白噪声序列，经差分后序列的白噪声检验结果为：(array([8.971 632 71]), array([0.002 742 03]))。输出的值为0.002 7，显著小于0.05，根据上述结果可以得出：原始序列经过一阶差分成功转变成了平稳非白噪声序列。模型检验：采用DW检验，检验结果为1.778 747 098 947 026 4，接近2，表明模型不存在自相关性[12]。

3 结论

本文首先借助灰色关联度分析得出音乐间的相似程度主要在于popularity、year、loudness、energy和acousticness这几个指标上。然后利用K-Means聚类分析法探究出流派中的艺术家不一定比流派间的艺术家更相似的结果。流派内部与流派之间的相似之处主要在于指标loudness和popularity上，流派内部的相似之处主要在于loudness，一定程度在popularity上相似。流派的区别主要在于energy、acousticness和year这3个指标上。最后，根据绘制流派指标在各时间段的簇状图，建立了时间序列ARMA模型，以这些数据为基础分析预测得出向后5期的不同流派的演变预测结果。

[1] 朱林. 基于灰色关联聚类的推荐算法研究[D]. 哈尔滨:哈尔滨师范大学, 2020.

[2] 黄杜鹃, 魏天, 王科, 等. 基于多元分析与灰色理论的水资源利用的定量研究[J]. 辽宁工业大学学报: 自然科学版, 2019, 39(6): 384-388.

[3] 刘怡, 周凌云, 耿纯. 京津冀产业协同发展评估:基于区位熵灰色关联度的分析[J]. 中央财经大学学报, 2017(12): 119-129.

[4] 冮建伟, 蔡欣悦, 吴媚, 等. 基于灰色关联度对奶粉销售因素分析[J]. 辽宁工业大学学报: 社会科学版, 2019, 21(2): 33-36.

[5] 赵伟, 倪绿林, 李枫. 基于K-means聚类分析的ShadowsocksR流量识别研究[J]. 通信技术, 2020, 53(8): 1970-1975.

[6] 胡兰兰. 基于GPS出租车高收益热点区域推荐[D]. 温州: 温州大学, 2019.

[7] 刘微. 基于聚类分析的电子商务客户忠诚度研究[D]. 哈尔滨: 哈尔滨商业大学, 2016.

[8] 牛珊. 基于时间序列方法的天气衍生品定价研究[D]. 哈尔滨: 哈尔滨商业大学, 2016.

[9] 胡志朝. 基于电力物联网的数据可视化分析[D]. 温州:温州大学, 2019.

[10] 石月. 基于时间序列分析的松花江流域水质预测[D]. 哈尔滨: 哈尔滨师范大学, 2020.

[11] 张超. 基于时间序列法超短期负荷预测改进方法的研究[D]. 锦州: 辽宁工业大学, 2015.

[12] 葛娜, 孙连英, 赵平, 等. 基于ARIMA时间序列模型的销售量预测分析[J]. 北京联合大学学报, 2018, 32(4): 27-33.

Research on the Influencing Factors and Evolution Prediction of Music Genre Based on Mathematical Method

LI Meng1, ZHANG Feng1, LI Yong2

（1.School of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu 233030, China; 2.School of Economics, Anhui University of Finance and Economics, Bengbu 233030, China）

As a part of human cultural inheritance, music is closely related to human life. At the same time, different music schools have different influences on human social life, so it is necessary to study the development of music schools. Firstly, this paper analyzes the factors that affect music genres by using gray correlation analysis and K-mean clustering analysis, and then based on the existing data, establishes a time series ARMA model to predict the development trend of music genres in the next five years.

gray correlation analysis; K-means clustering analysis; ARIMA time series analysis; Python; MATLAB

10.15916/j.issn1674-3261.2022.02.014

F224

A

1674-3261(2022)02-0135-06

2021-06-16

国家自然科学基金资助项目(11601001)；全国大学生数学建模组委会后继研究(夏令营A1401)

李梦(2000-)，女，安徽肥东人，本科生。

李勇(1963-)，男，安徽蚌埠人，副教授，硕士。

责任编辑：刘亚兵