基于Mean Shift聚类的瞬时风功率密度预测研究

李奂其 王天龙 罗婷

（1.华北电力大学电气与电子工程学院，北京 102206；2.北京农学院国际学院，北京 102206）

0.引言

海上风电功率预测是做好电力调度的基本前提，也是确保电力系统安全稳定经济运行的重要保障，传统风功率的预测一般可分为物理模型法[1,2]和统计模型法[3-5]，但是海上风电的预测仍然存在着数据量巨大、难以处理等问题，相关研究人员利用统计方法对大量海上风电数据进行分类及简化，闫健[6]通过采用K均值聚类分析寻找相似性样本的方法，将不同海上风场气候特征进行数据驱动分类，采减小了数据量。K均值聚类需要提前指定K（即分类数量）和初始聚类中心，一旦这2个值选择不好，就有可能无法得到有效的聚类结果，甚至还可能导致死循环。

为了解决这一问题，本文提出了一种基于Mean Shift（均值漂移算法）的海上风功率预测方法，主要利用从NWP（Numerical Weather Prediction，即数值天气预报）中获得的数据进行Mean Shift聚类，减小数据量，然后利用LSTM神经网络算法建立风功率密度的预测模型，从而对风功率密度进行预测。

1.模型的建立

1.1 影响风功率的因素

海上风电功率受多种因素的影响，除了机组自身各种参数的限制之外也受到许多自然条件的影响，本文选择风速、风向、温度、湿度、大气压力等自然因素来进行风功率的预测。

本文选取德国Alpha Ventus海上风电场2021年1月1日到1月30日的数据来进行验证，其拥有12台风电机组，于2010年4月投产。图1（a）为Alpha Ventus 12台风电机组的坐标图。图1（b）是某日24小时之内各风电机组处的风速变化三维图。由图1可知，在同一个风电场内，不同机组由于距离较近，在读取大部分的风速、风向等自然条件数据时，可以把Alpha Ventus海上风电场看作一个点，数据采用平均值进行分析和预测。

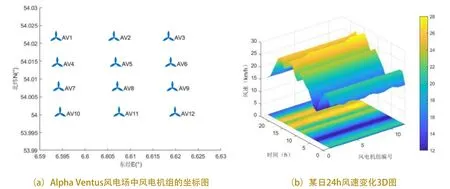
图1 Alpha Ventus风电机组的坐标图和风速变化三维图

1.2 相关性分析

为了定量描述风速、风向、气温等输入特征与风电输出功率的相关程度，本文根据斯皮尔曼关系数（Spearman Correlation Coefficient）对其进行可视化处理。将集合x、y中的元素对应相减得到一个排行差分集合di，1<=i<=N。

随机变量X、Y之间的斯皮尔曼等级相关系数可以由x、y或者d计算得到，其计算方式如下所示，由排行差分集合d计算而得：

1.3 Mean Shift聚类与LSTM

Mean Shift是一种基于核密度估计的爬山算法，目前主要被应用与聚类、图像分割、跟踪等方面。相对于K均值聚类算法，Mean Shift聚类算法不需要预先设定簇的个数，和样本中心点的位置，这些都是通过计算机的迭代而得到。同时，该算法也具有较为稳定的聚类结果[7]。

为了能够更加准确地预测风电场各时间段内的WPD（顺时风功率密度），本文建立了基于LSTM（长短时记忆神经网络）的预测模型[8]。

2.结果与讨论

2.1 斯皮尔曼相关系数分析

图2为影响因素相关系数矩阵，可以看出海上风电的众多影响因素是相互关联且复杂多样的，在实际机组风电功率密度计算中还要考虑风机运行的尾流效应以及风向与功率损失之间的关系，所以我们采用统计方法，用神经网络对相关风电功率进行预测。

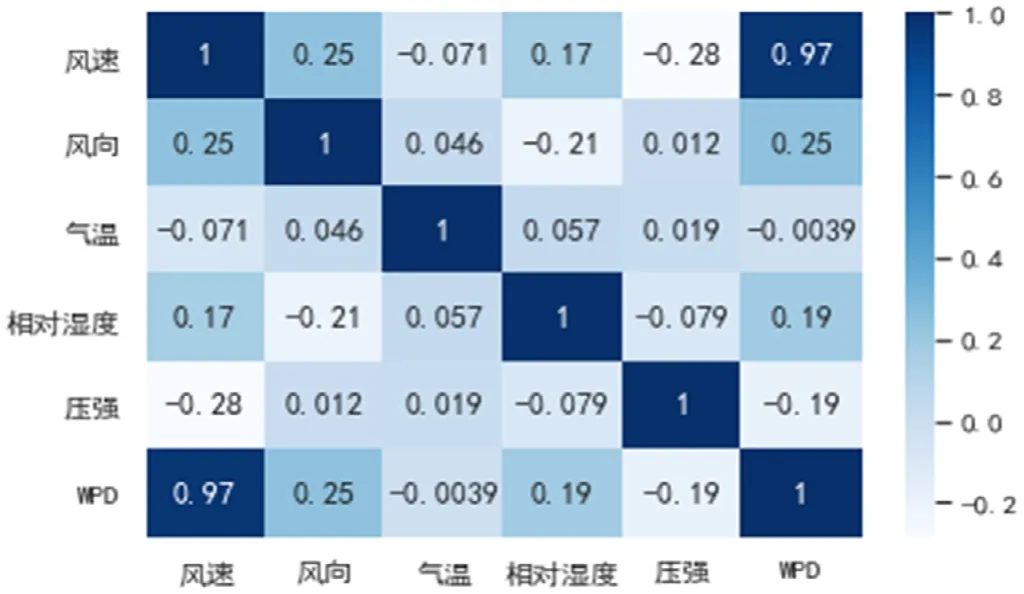
图2 斯皮尔曼相关系数矩阵图

2.2 Mean Shift聚类结果分析

通过调节不同的搜索半径r值，改变聚类个数，得到结果如图3所示。

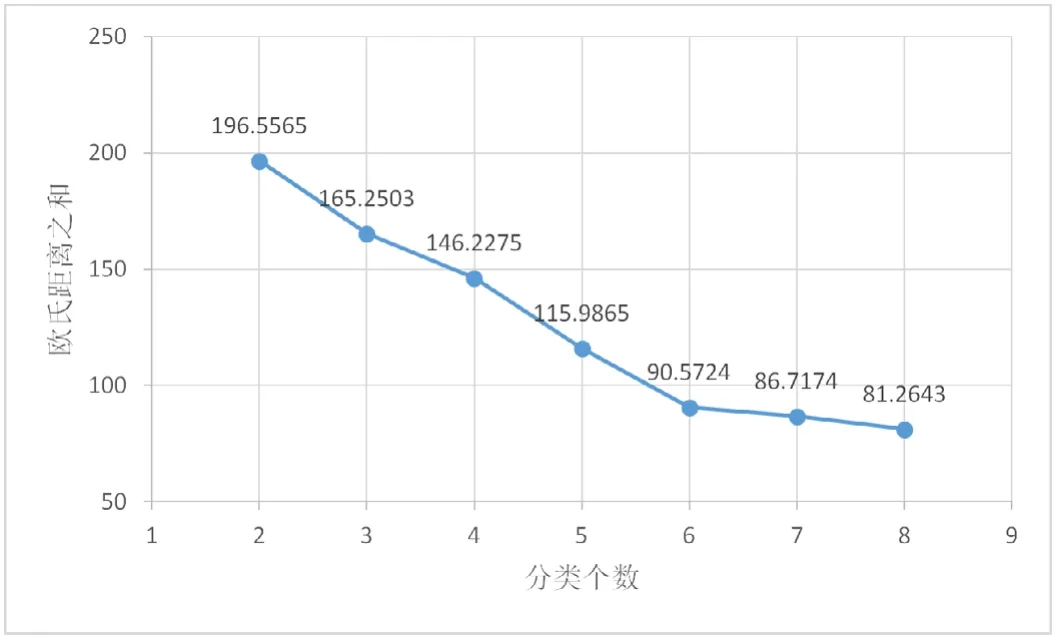
图3 欧式距离之和与聚类情况关系图

由上图3可以看出，分类数越多，欧氏距离之和就越小，当分类个数超过6时，当分类个数继续增加时，而欧氏距离之和减小却不明显，本文选择合适的搜索范围，使其聚类个数为6。对Alpha Ventus海上风电场2021年1月的数据的聚类结果如表1所示。通过比较各样本点风速曲线和聚类中心风速曲线，发现其形状有很强的相似性，聚类效果良好。如图4所示。

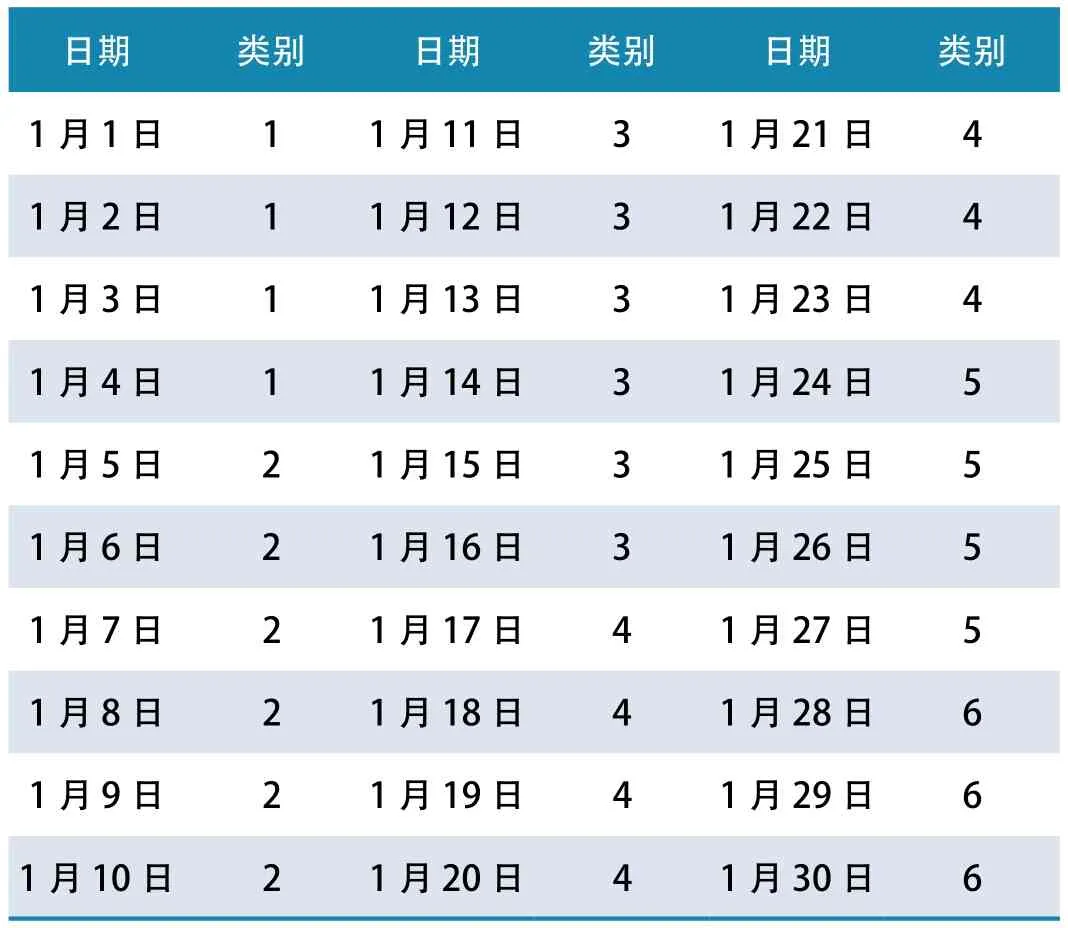
表1 对Alpha Ventus海上风电场2021年1月的数据的聚类结果

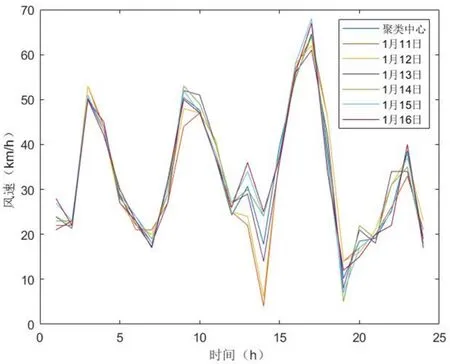
图4 第三类样本点与该聚类中心的风速曲线

2.3 基于LSTM的预测结果分析

本文采用2021年2月1日的前15h的数据来进行对预测数据的验证。首先根据（3）式计算2月1日数据到6个聚类中心的欧氏距离，结果图5所示。发现该点距离第5类聚类中心点的欧氏距离最小，所以，2月1日属于第5类。用1月24日至27日的风向、风速、温度、湿度、大气压力等数据进行LSTM网络的训练，再将2月1日的上述数据输入网络，对该日前15h的WPD进行预测。此外，为了使结果更加可信，本文还采用3次回归预测的方法进行对照。预测结果如图6所示。

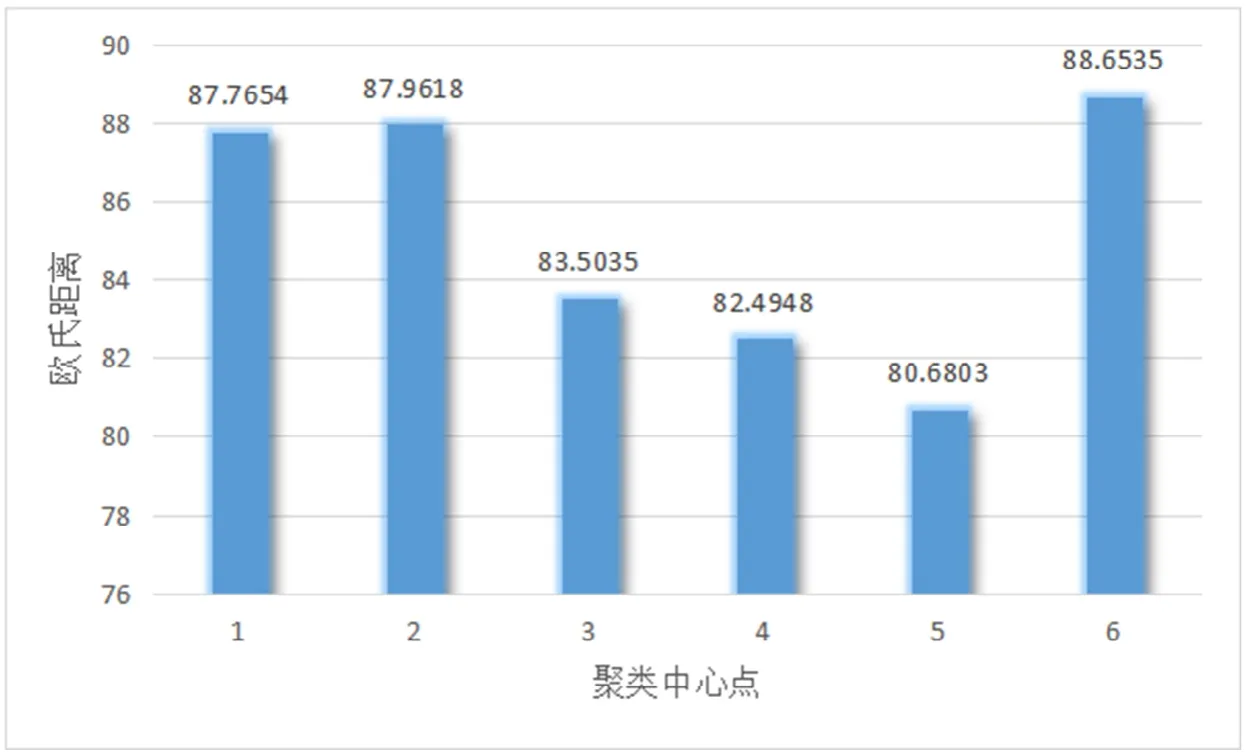
图5 2月1日数据距离各中心点的欧氏距离

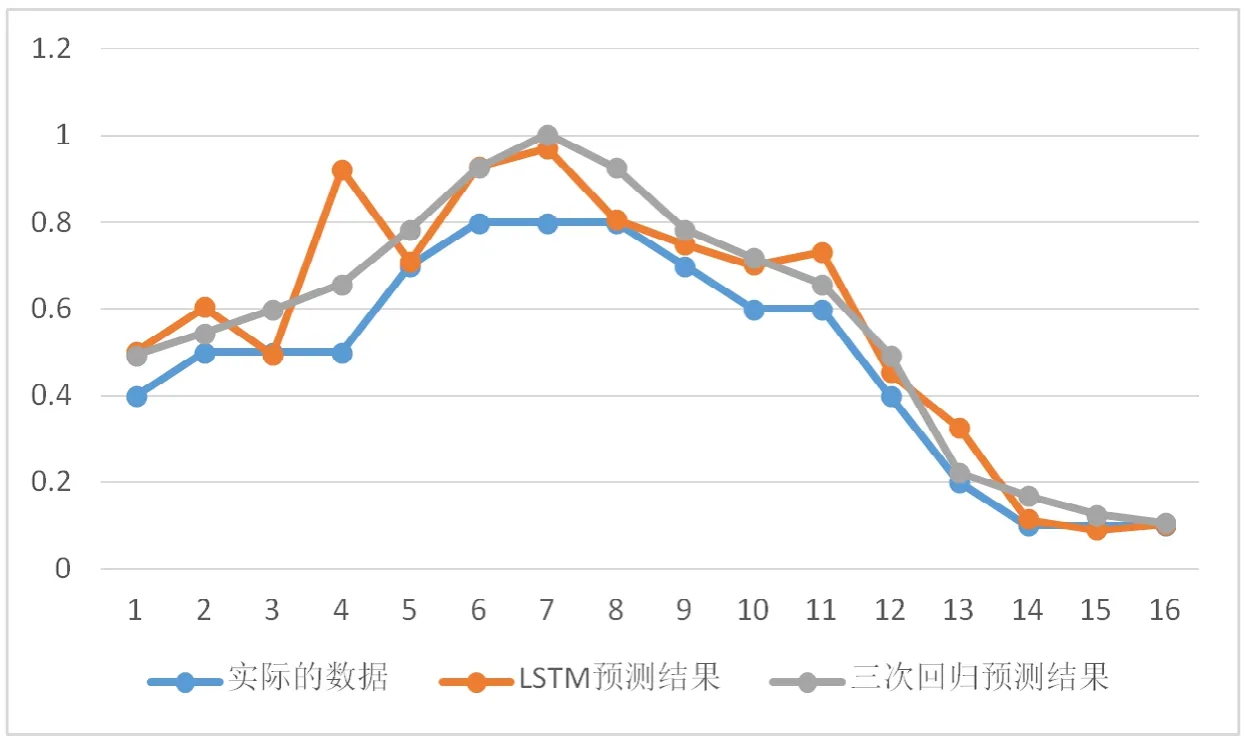
图6 2月1日前15h的WPD预测情况

由于WPD的值比较小，本文通过采用SMAPE (Symmetric Mean Absolute Percentage Error，即对称平均绝对值百分比误差)来衡量测量结果的准确性。SMAPE的范围为[0，+∞），且该值越小，说明预测模型的准确度更高，当预测值和真实值完全吻合时，SMAPE为0，即该模型为完美模型；当SMAPE大于100%时，该模型为劣质模型。根据式（3）进行了SMAPE的计算。

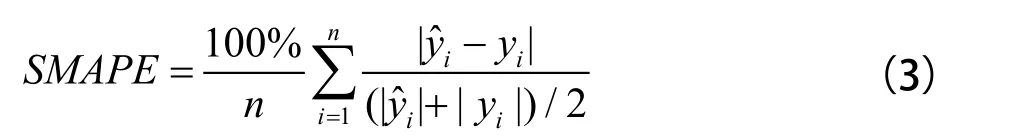
根据计算，2月1日前15h的LSTM预测数据的SMAPE为16.58%，而用3次回归预测所得数据的SMAPE为18.05%。可见该预测方法的误差在可以接受的范围内，比3次回归预测更加准确，故该模型在一定程度上可以对WPD进行预测。

3.结论

本文提出一种基于Mean Shift聚类算法的WPD预测方法，建立了以从NWP获得的风向、风速、温度、湿度、大气压力等参数预测WPD的预测模型，并且采用2月1日德国Alpha Ventus海上风电场的数据进行验证得出以下结论：

（1）由斯皮尔曼关系数可知，WPD和风速的相关性最大，而其他自然条件因素与WPD的相关性不大，因此在建立模型聚类和预测时，适当提高风速的权重，有利于预测结果的准确度的提高。（2）由于每一天的自然条件等都存在着一定的相似性，因此可以采用Mean Shift聚类分析的方法来对数据进行聚类，再通过欧氏距离计算预测日的数据属于哪一类，最后再用该类的数据进行LSTM网络的训练，从而进行预测，有效减少需要处理的数据量，大大减少程序运行时间，结果的准确性也会因此而降低。