基于响应面的焊接件加肋板结构参数优化设计

周鑫

（中国直升机设计研究所，江西景德镇 333001）

0.引言

焊接件加肋板结构在直升机强度试验中是一种常见的结构形式，加肋板的焊接件在承载过程中能够提高结构的承载能力以及结构的刚度，并且能够提高结构的固有频率，降低其振动响应等[1-2]。焊接件加肋板结构的承载能力很大程度上取决于肋板的结构参数以及布置位置，不合理的加肋板结构固然能保证结构的强度要求，但是也引起结构用钢量较大，增加了制造成本，因此优化肋板的结构参数是有必要的[3]。

传统的优化方法是根据经验以及有限元分析对结构进行加强或者对材料冗余部位进行削减，传统方法需要反复验证从而造成效率较低并且改进的结构的最优性难以保证。随着计算机的发展，多目标优化设计方法在机械设计领域中得到长足的发展，并且不断发展出遗传优化算法，神经网络算法以及粒子群算法等用于求解复杂的、带有约束的多目标优化问题。基于响应面法的多目标优化设计避免了试验周期长，试验结果对真实结果拟合误差大的缺点[4]。

本文以焊接结构件为研究对象，在ANSYS中进行参数建模，然后进行静力学分析，根据应力、变形及质量情况，采用Design Xplorer模块对焊接件肋板的结构参数进行优化。

1.模型建立

本文利用ANSYS软件Design Modeler模块进行参数化建模，模型如图1所示。肋板的结构参数表示如图2所示。

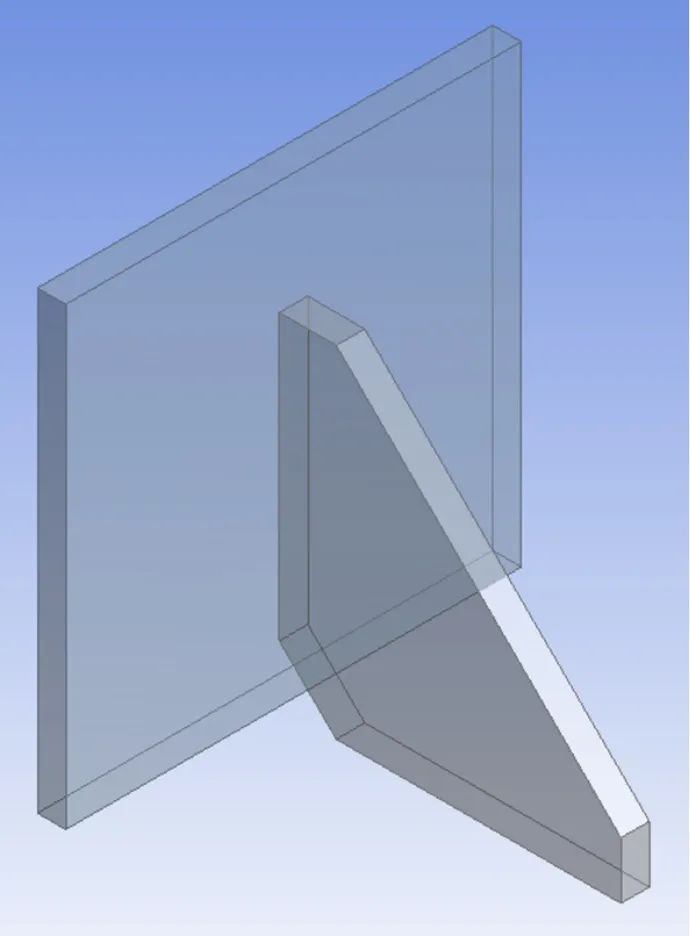
图1 加肋板结构

图2 肋板结构参数

将带参数的肋板结构三维模型导入静力学分析模块，进行相关参数设置和静力学分析。材料设置为结构钢，密度为7850kg/m3，弹性模量为200Gpa，泊松比0.3。网格设置为六面体网格，网格单元尺寸为1mm，节点数73222，网格数量47728。实际状态下肋板与立板的连接方式为焊接，为简化模型设置两接触面之间用绑定接触代替。立板背面施加在沿肋板长度的载荷，边界条件为立板底面和肋板底面设置为固定约束。根据上述加载及边界条件，求解得到等效应力和变形云图，另外为避免应力奇异现象出现，在不影响肋板结构的情况下对存在的尖角进行圆角处理，求解结果如图3和图4所示。

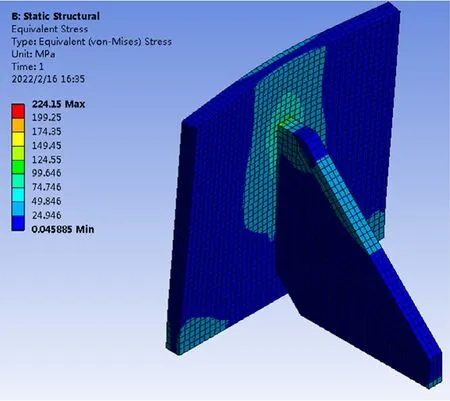
图3 加肋板结构应力云图

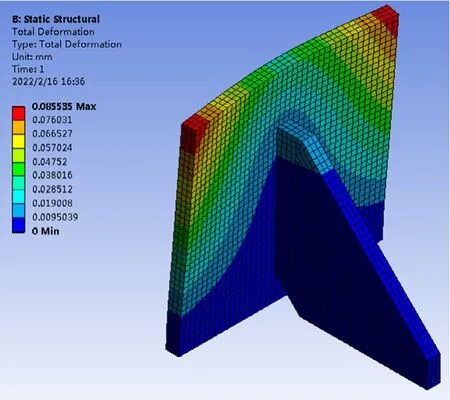
图4 加肋板结构变形云图

2.优化设计

优化设计的本质是将实际的工程问题转化为数学问题，基于响应面的多目标优化设计是根据所设置的边界条件及外部载荷建立数学模型，并在设计变量范围内生成样本点，通过样本点计算响应面，对响应面上的设计点经过多次迭代，从而得到目标函数极值[5]。根据所求的极值，结合实际工程情况对比优化结果，从而产生符合要求的最优解。本文中优化设计的目的是在保证结构的强度和刚度情况下，实现结构的轻量化。设计变量为肋板长度L1，肋板高度H1，倒角长度L2，上缘长度L3，倒角高度H2，右缘高度H3，肋板厚度t，目标函数是使得该结构的强度和刚度最大并且材料最少，可等效为最大等效应力和最大变形最小，质量最小，对优化肋板结构的数学模型如下[6-7]：

其中 xi（i=1，2，3）是状态变量，Hi、Li（i=1，2，3）和t是设计变量。

在进行优化设计前应进行相关参数的敏感性分析，敏感性分析的作用是确定输入输出参数对结构件尺寸的影响程度，得到输入输出参数的敏感性分析结果后，能够直接找到对目标函数影响最为显著的输入参数，首先对影响显著的参数作为优化对象，这可以使得优化过程中的优化参数数量的减少，降低了运算量和运算时间成本[8]。相关参数的敏感性分析结果如图5所示，根据敏感性分析结果可知各个输入参数对优化变量的影响程度不同，其中肋板高度H1对加肋板结构的质量、强度和刚度变量影响较为显著分别达到了0.33、-0.89和-0.86；肋板厚度t对质量和应力影响较为显著，其值分别达到了0.81、-0.30和-0.40；而肋板长度L1只对结构的质量和变形影响较大，对应力影响较小；上缘长度L3对质量和应力影响较大。另外，敏感性分析结果显示的影响趋势也是符合预期的。

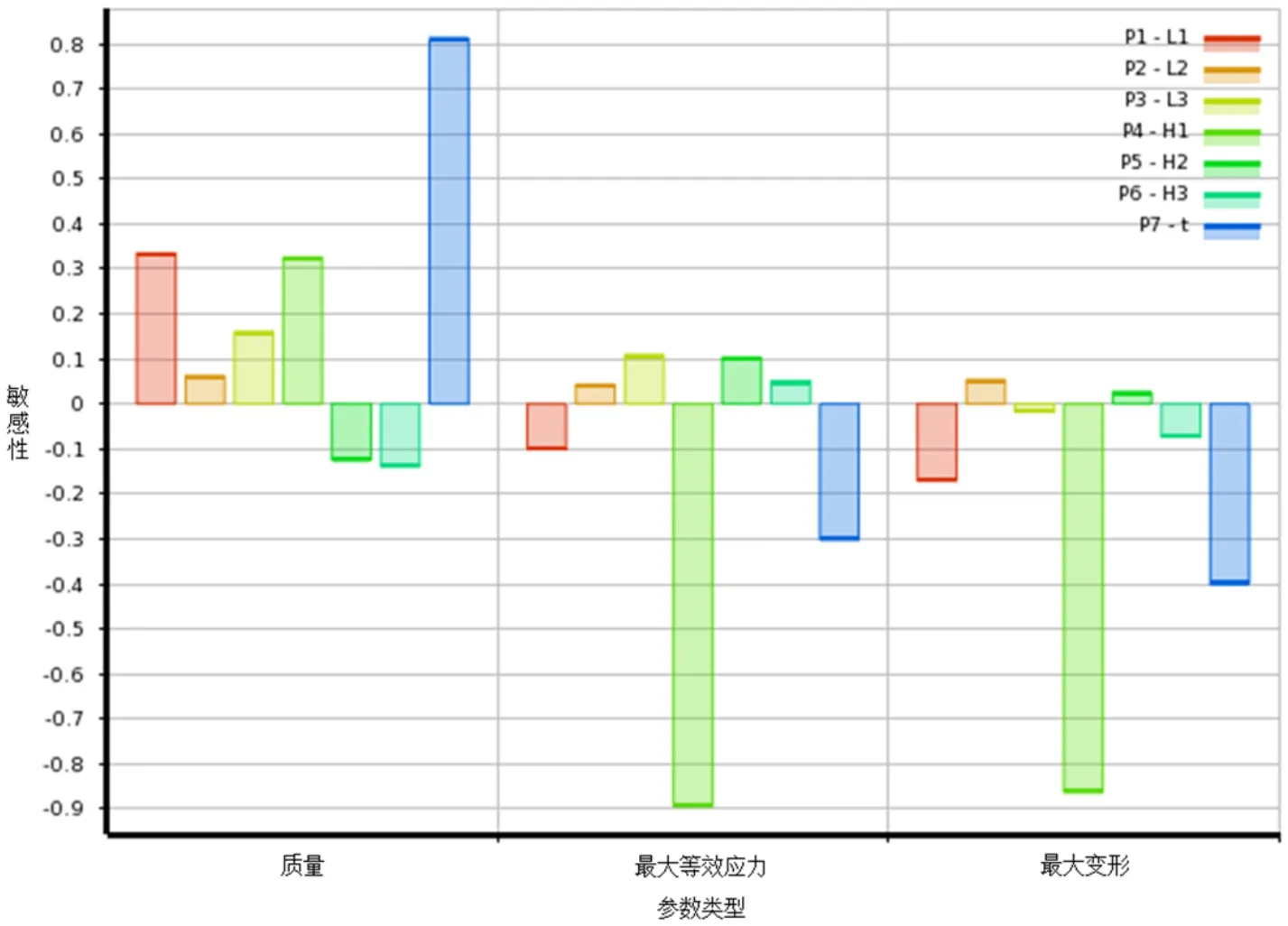
图5 肋板结构参数敏感性分析

响应面的构造应该先生成试验点，而试验点的选取对响应面的精度有很大的影响，试验点选择不合理有可能造成响应面无法拟合。目前的试验点的设计方法主要有Central Composite Design（CCD）、Optimal Space-Filling Design（OSF）、Box-Behnken Design（BBD）等，本文采用OSF方法生成试验点。常见构造响应面的模型主要有Genetic Aggregation、标准响应面、Kriging、非参数回归（Non-parametric Regression）和神经网络模型[9]，本文选择Kriging模型构造响应面，该类型的响应面模型适合非线性参数模型。响应面模型的拟合程度直接影响着后续优化结果的准确性，评估响应面准确性的参数指标主要是决定系数R2、均根方差RMSE，相对平均绝对误差RAAE。依据图6所示响应面的预测值与计算值之间的偏差，可以发现局部误差较大区域并对该区域进行细化，经过两次添加验证点细化，Kriging模型建立的响应面具备相应的精度，其评估参数如表1所示。

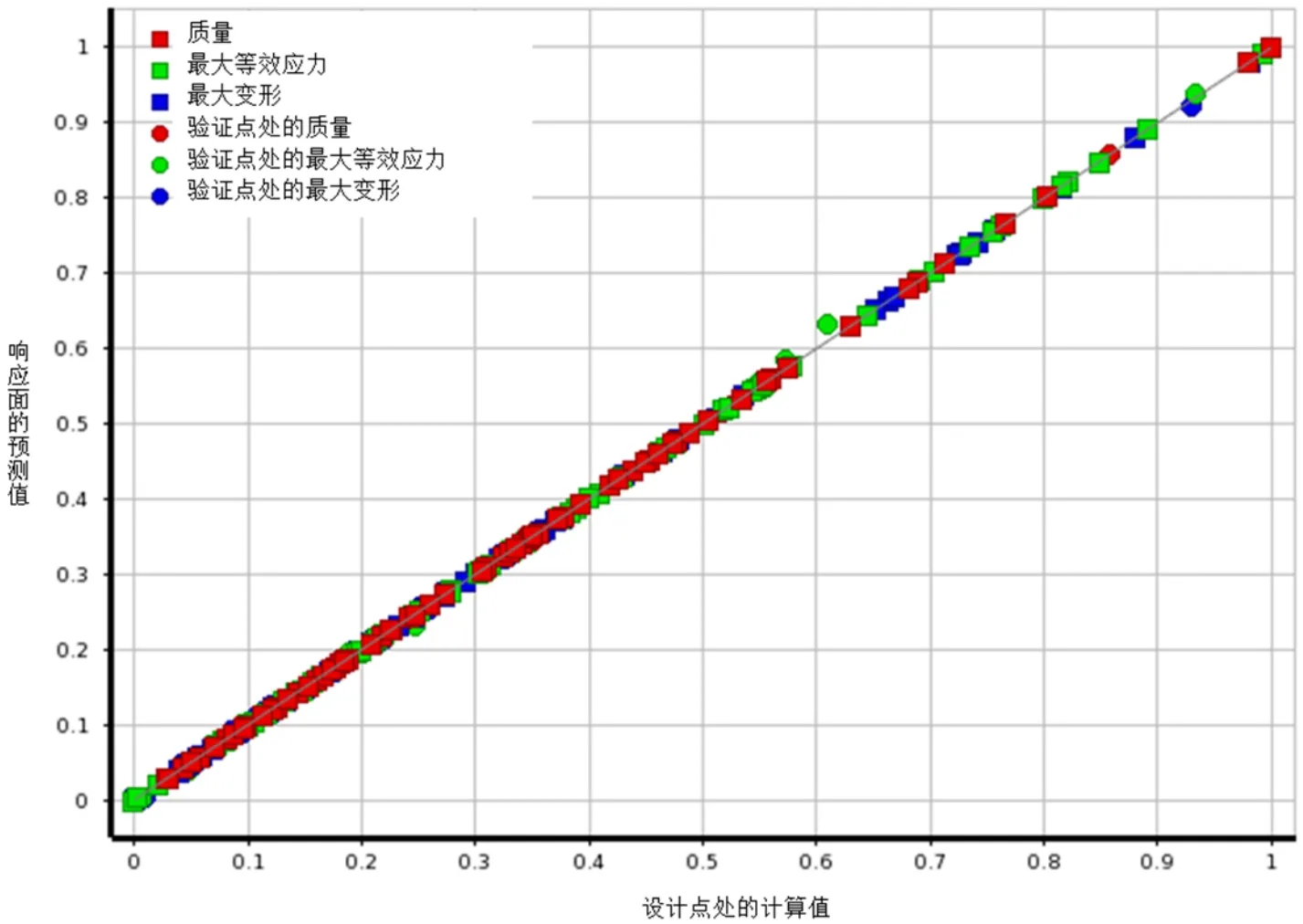
图6 响应面设计点处计算值与响应面预测值的偏差

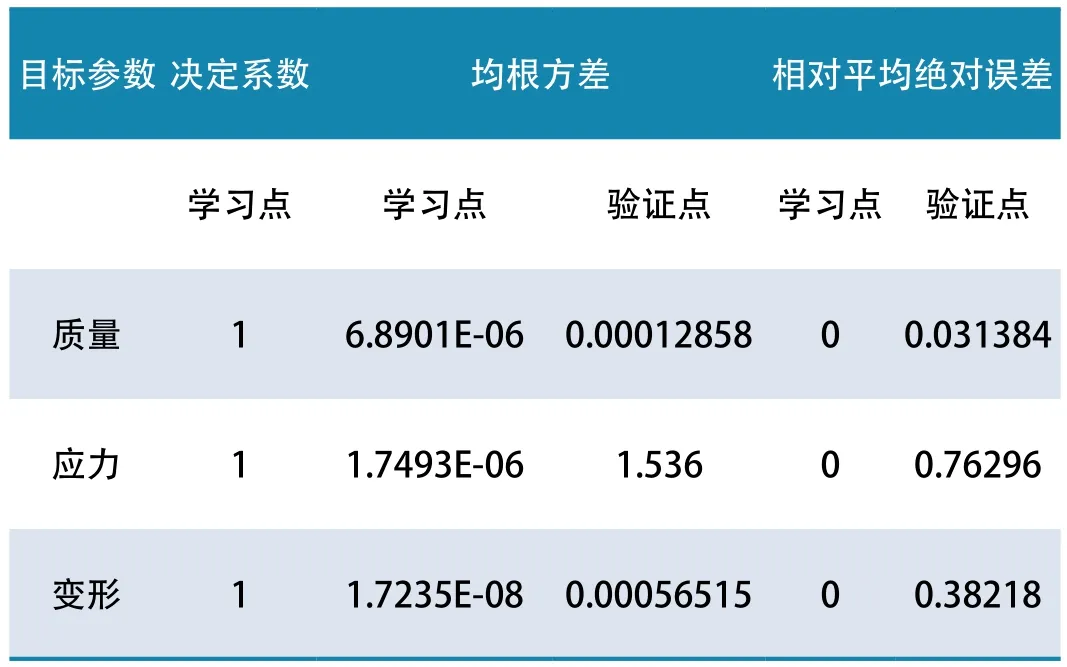
表1 Kriging模型评估

3.优化设计结果

根据对肋板结构参数敏感性的分析，肋板高度H1，肋板长度L1，上缘长度L3和肋板厚度t对状态变量质量、强度和刚度影响较为显著，故对该四类参数进行响应面分析，响应面分析结果如图7～图10所示。

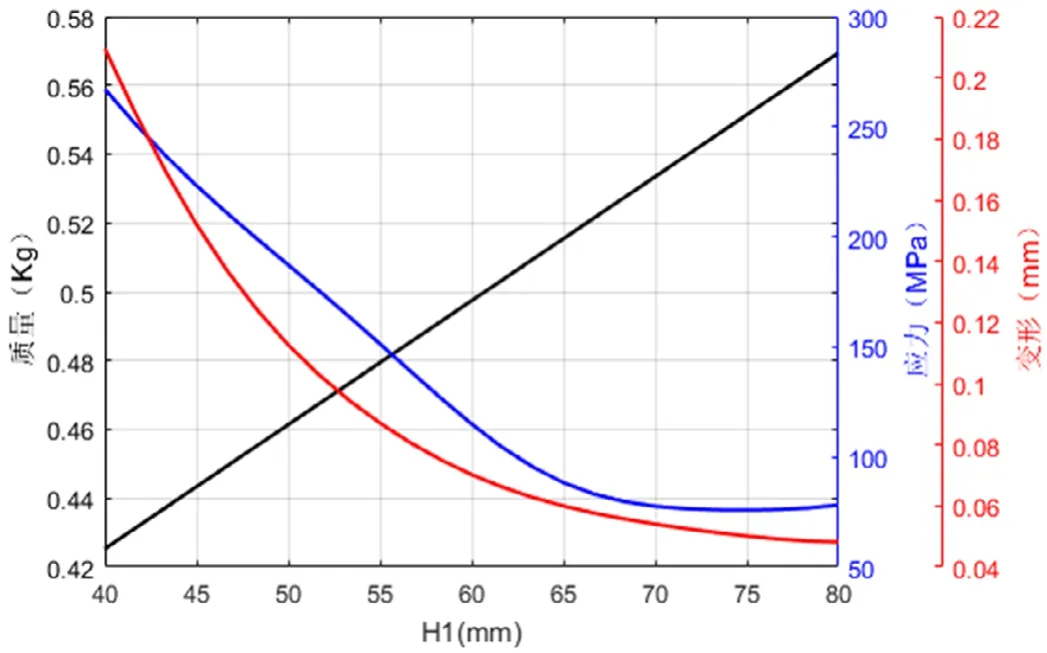
图7 肋板高度H1对质量、应力和变形的影响

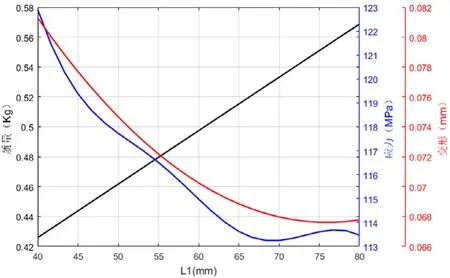
图8 肋板长度L1对质量、应力和变形的影响

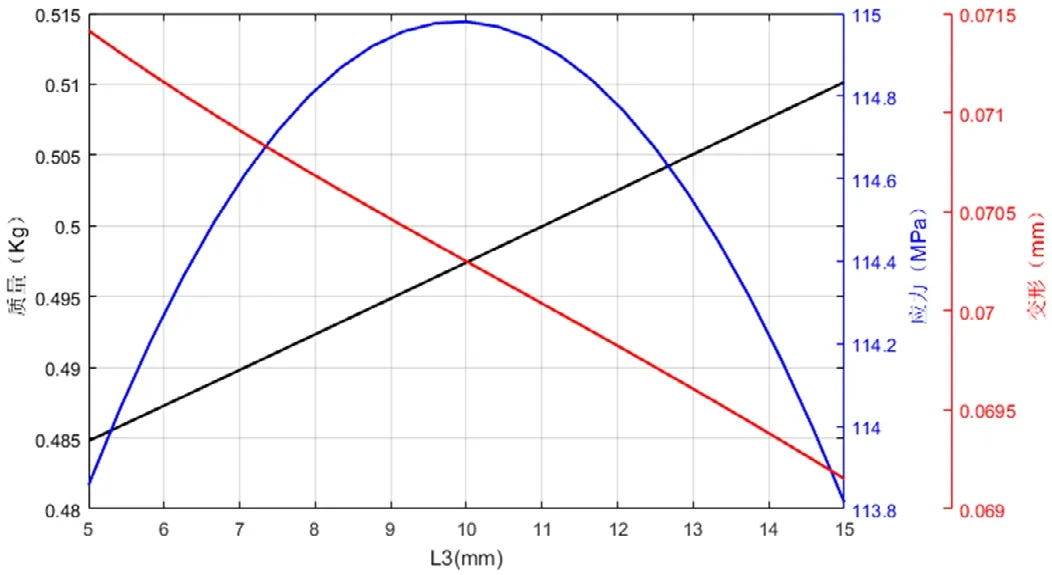
图9 右缘高度L3对质量、应力和变形的影响

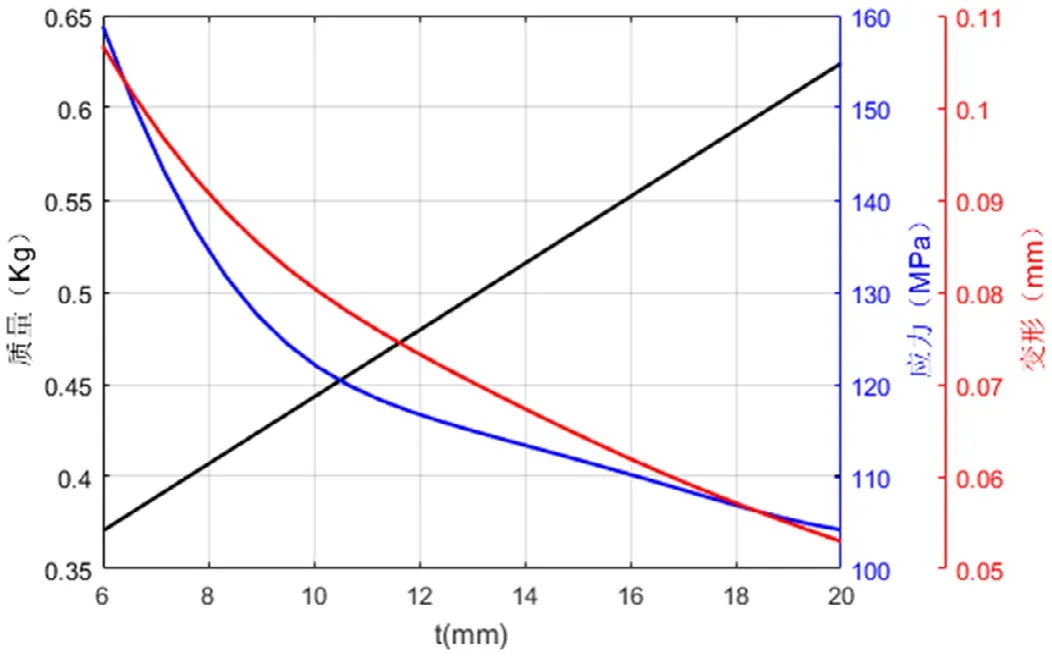
图10 肋板厚度t对质量、应力和变形的影响

从图上可以看出，该结构的质量参数与其尺寸参数成正比，这和预期的结果是一致的。最大变形量基本上是随着结构尺寸参数的增大而减小，表明其刚度随着尺寸增大而增加，但是各个结构尺寸参数对变形量的影响程度均不相同，H1、L1和t影响程度基本上呈现出逐渐减少的趋势，值得注意的是L3和最大变形量之间存在极强的线性关系。最大等效应力随着肋板长度、高度与厚度参数增加而较小，并且其对最大应力的影响程度随着尺寸参数的增加而降低。另外值得注意的是随着L3的增加最大等效应力呈现出先增大后减小的抛物线趋势，并且在10mm附近出现极大值点。

基于Kriging建立的响应面模型，设定约束目标为质量最小，最大等效应力最小和最大变形最小。优化方法采用MOGA，初始迭代数目设定为4000，迭代20次，每次迭代数量为800。如图11所示为经过20次迭代获得的质量与最大等效应力的帕累托解，使用筛选算法可以生成3个备选设计点，如表2所示。3个备选设计点在质量，最大等效应力和最大变形方面相差不大，根据本文拟定的优化目标是材料用料最少，即结构尺寸最小，且承载能力最高、变形最小，故在满足强度的情况下选择质量最小的设计点即样本点6。样本点6结构尺寸在质量减少8.7%的情况下，强度提高了15.3%，刚度提高了8.8%。另外，发现肋板高长比在1.3～1.5，肋板上缘长度5mm～6mm，肋板厚度在7mm～8mm范围内对减少材料用料提高结构强度方面较为合理。

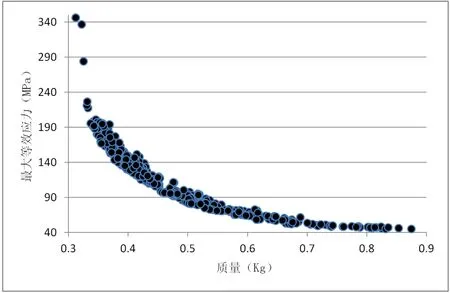
图11 质量与最大等效应力的帕累托解

表2 备选设计点

4.结论

本文介绍了直升机强度试验过程中焊接件加肋板结构参数优化方法，基于Kriging模型建立响应面，采用多目标遗传算法MOGA对目标参数进行优化获得优化后的结构参数。在敏感性分析过程中，对性能目标影响显著的主要是肋板长度、高度、上缘长度和肋板厚度参数，对该四种参数进行优化分析过程中发现上缘长度与应力呈现抛物线形式，并且在L3=10mm附近存在极大值点。另外，各参数对强度影响显著性随着结构尺寸的增大而逐渐减少。最后，结构尺寸在质量减少8.2%的情况下，强度提高了16.3%，刚度提高了11.3%，对所生成的备选设计点分析，合理的肋板高长比在1.3～1.5，合理的肋板上缘长度≈5mm，而肋板厚度在7mm～8mm范围内较为合理。