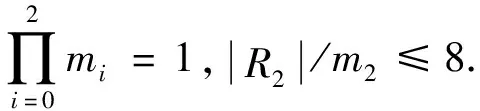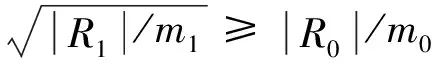有限交换环上Ramanujan二次单位一-匹配双凯莱图
2022-06-08苟小丽
苟小丽
(兰州交通大学 数理学院,甘肃 兰州 730070)
0 引言
本文所考虑的图均为简单无向图.设图G的顶点集为V(G)={1,2,…,n},它的邻接矩阵为A=(aij)n×n,其中当顶点i和j相邻时,aij=1; 否则aij=0.图G的特征值是其邻接矩阵的特征值.
设A(G)的互异特征值为λ1>λ2>…>λk,且它们的重数分别为m(λ1),m(λ2),…,m(λk),则图G的谱记为
一个有限k-正则图G称为Ramanujan图[1],如果
其中:λ(G)为G的不同于±k的特征值绝对值的最大值.关于Ramanujan图及相关扩展图的研究, 可参考文献[2-8].
1878年,A Cayley 为解释群的生成元和定义关系首次提出凯莱图的概念.1992年, Resmini 和 Jungnickel[9]定义了双凯莱图.
设H是一个具有单位元1H的群,R,L,S是H的子集,且1H∉R=R-1,1H∉L=L-1,则H上的双凯莱图BC(H;R,L,S)是指以H×{0,1}为顶点集的无向图,且(h,i)和(g,j)相邻,当且仅当以下条件之一成立:
(i)i=j=0且gh-1∈R;
(ii)i=j=1且gh-1∈L;
(iii)i=0,j=1且gh-1∈S.
特别地,若S由H的单位元构成, Kovács 等[10]称其为H上的一-匹配双凯莱图.
关于(一-匹配)双凯莱图的一些组合性质和代数性质,其中包括弧传递性、强正则性、自同构和点传递性,可参考文献[9-12].
设R是有单位元1≠0的有限交换环,R×表示其单位的集合.局部环是有唯一极大理想的交换环[13].由文献[13-14]可知,若R是具有唯一极大理想M的局部环,则R×=RM.每个有限交换环可表示为有限局部环的乘积,且这种分解在不计此类局部环的排列次序时是唯一的.因此,后续讨论总是基于以下假设.
假设1[4]R=R1×R2×…×Rs是具有单位元1≠0的有限交换环,其中Ri是具有mi阶极大理想Mi的局部环.设
|R1|/m1≤|R2|/m2≤…≤|Rs|/ms.
显然,
(1)
定义1[5]给定一个交换环R,R上的二次单位凯莱图GR定义为R关于TR=QR∪(-QR)在加法群上的凯莱图Cay(R,TR),其中QR={u2:u∈R×},即GR有顶点集R,使得x,y∈R相邻,当且仅当x-y∈TR.
这个概念是Zn上的二次单位凯莱图GZn的推广[15], 当n≡1(mod 4)且为素数时, GZn是n阶Paley图.随着对GZn结构性质的进一步研究,de Beaudrap将GZn在n的素因子上分解为张量积, 还计算了GZn的直径, 并给出GZn是完美的条件[15].
文献[16]基于单位凯莱图的概念定义了单位一-匹配双凯莱图.本文类比单位一-匹配双凯莱图的概念, 在二次单位凯莱图的基础上定义了二次单位一-匹配双凯莱图的概念.
定义2给定一个交换环R,R上的二次单位一-匹配双凯莱图GR定义为R加法群上的一-匹配双凯莱图BC(R;TR,TR,{0}),其中TR=QR∪(-QR),QR={u2:u∈R×}.
2015年,刘晓刚等[5]给出了二次单位凯莱图是 Ramanujan 图的等价刻画.受此启发,本文主要讨论了二次单位一-匹配双凯莱图是 Ramanujan 图的等价条件.
1 二次单位一-匹配双凯莱图
两个图G和H的笛卡尔积记作G□H,其顶点集为V(G)×V(H),顶点(u,v)和(x,y)相邻当且仅当v=y且u和x在G中相邻,或u=x且v和y在H中相邻.
引理1[17]设G和H是两个图,其特征值分别为λ1,λ2,…,λn和μ1,μ2,…,μm,则G和H的特征值为λi+μj,1≤i≤n,1≤j≤m.
引理2[5]设R是具有m阶极大理想M的局部环,则
(1)若|R|/m≡1(mod 4),则
(2)若|R|/m≡3(mod 4),则
Spec(GR)=
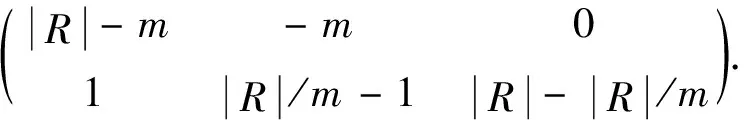
根据二次单位一-匹配双凯莱图和笛卡尔积的定义,有GR≅Cay(R,TR)□P2=GR□P2,其中P2为2长路.由引理1和2可得如下结论.
定理1设R是具有m阶唯一极大理想M的局部环,则
(1)若|R|/m≡1(mod 4),则
(2)若|R|/m≡3(mod 4),则
Spec(GR)=
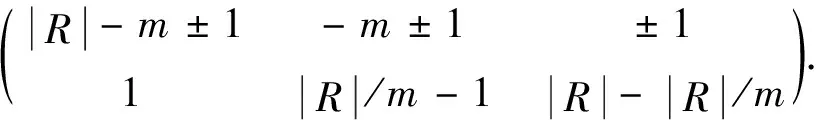
引理3[5]设R如假设1所示,则GR=GR1⊗GR2⊗…⊗GRs当且仅当至多存在一个Rj,使得-1∉QRj.
定理2设R如假设1所示,|Ri|/mi≡1(mod 4),1≤i≤s,则
GR=(GR1⊗GR2⊗…⊗GRs)□P2.
证明根据二次单位一-匹配双凯莱图和笛卡尔积的定义,有
GR≅Cay(R,TR)□P2=GR□P2,
其中P2为2长路.因为|Ri|/mi≡1(mod 4),1≤i≤s,所以-1∈QRi/Mi,1≤i≤s,于是-1∈QRi,1≤i≤s,从而由引理3可知,
GR=GR1⊗GR2⊗…⊗GRs,
故GR=(GR1⊗GR2⊗…⊗GRs)□P2.
令
λA,B=(-1)|B|·
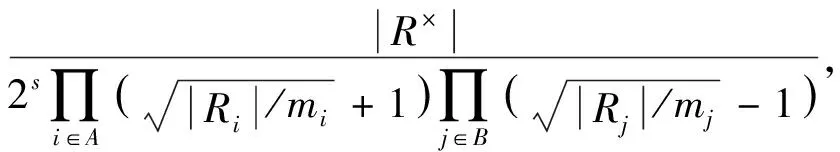
其中,A,B为{1,2,…,s}的不交子集[5].特别地,λ∅,∅=|R×|/2s.
引理4[5]设R如假设1所示,|Ri|/mi≡1(mod 4),1≤i≤s,则GR的特征值为
(1)λA,B,重数为
其中,所有的(A,B)对均为{1,2,…,s}的子集,且A∩B=∅;
(2)0,重数为
|R|-
由引理1, 定理2和引理4可得:
定理3设R如假设1所示,|Ri|/mi≡1(mod 4),1≤i≤s,则GR的特征值为
(1)λA,B±1,重数为
其中,所有的(A,B)对均为{1,2,…,s}的子集,且A∩B=∅;
(2)±1,重数为
|R|-
引理5[5]设R如假设1所示,|Ri|/mi≡1(mod 4),1≤i≤s,R0是具有m0阶极大理想M0的局部环,且|R0|/m0≡3(mod 4),则GR0×R的特征值为
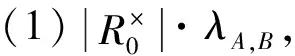
其中,所有的(A,B)对均为{1,2,…,s}的子集,且A∩B=∅;

其中,所有的(A,B)对均为{1,2,…,s}的子集,且A∩B=∅;
(3)0,重数为
|R|-
由引理1, 定理2和引理5可得:
定理4设R如假设1所示,|Ri|/mi≡1(mod 4),1≤i≤s,R0是具有m0阶极大理想M0的局部环,且|R0|/m0≡3(mod 4),则GR0×R的特征值为
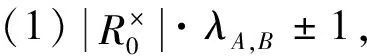
其中,所有的(A,B)对均为{1,2,…,s}的子集,且A∩B=∅;
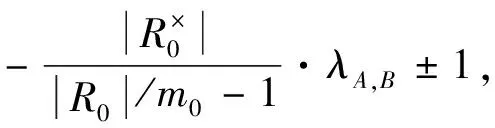
其中,所有的(A,B)对均为{1,2,…,s}的子集,且A∩B=∅;
(3)±1,重数为
|R|-
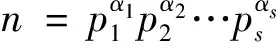
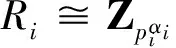
推论1(1)若p≡1(mod 4)为素数,且α≥1为整数,则
Spec(GZpα)=


(2)若p≡3(mod 4)为素数,且α≥1为整数,则
Spec(GZpα)=
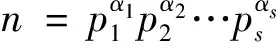
(1)

(2)±1,重数为

(1)

(2)
(-1)|B|+1·

重数为
其中所有的(A,B)对均为{1,2,…,s}的子集,且A∩B=∅;
(3)±1,重数为
2 Ramanujan二次单位一-匹配双凯莱图
引理6[18]设R是具有m阶唯一极大理想的有限局部环,则存在素数p使得|R|,m和|R|/m都是p的幂次.
定理5设R如假设1所示,|Ri|/mi≡1(mod 4),1≤i≤s,R0是具有m0阶极大理想M0的局部环,且|R0|/m0≡3(mod 4),则
(1)GR0是Ramanujan图,当且仅当
(2)GR是Ramanujan图,当且仅当R≅Fq,其中q≡1(mod 4)为素数的幂;
(3)GR0×R是Ramanujan图,当且仅当
R0×R≅F3×F9.
证明由文献[5]可知,GR0的正则度为|R0×|=|R0|-m0,GR的正则度为|R×|/2s,GR0×R的正则度为|R0×||R×|/2s.则由引理1和定理2可知,GR0的正则度为|R0|-m0+1,GR的正则度为|R×|/2s+1,GR0×R的正则度为|R0×||R×|/2s+1.
(1)根据定理1(2),当|R0|-m0-1≥m0+1,即|R0|≥2m0+2时,GR0是Ramanujan图
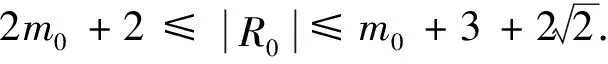
当|R0|-m0-1≤m0+1,即|R0|≤2m0+2时,GR0是Ramanujan图


(2)根据定理3,GR是Ramanujan图

λA,B±1≠±(|R×|/2s+1).

因为|λA,B±1|≤|λA,B|+1≤|λ∅,{1}|+1≠|R×|/2s+1,所以GR是Ramanujan图
(2)

(3)
又因为
则当s≥4时,由式(1)可知,
|R×|/2s≥
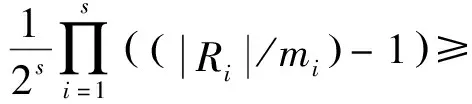
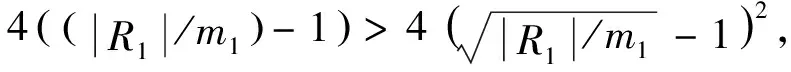
即式(3)不成立,所以GR不是Ramanujan图.
下面考虑1≤s≤3的情况.
情形1s=1.
若m1≥8时,以上不等式不成立,所以GR不是Ramanujan图.
假设m1≤7,因为|R1|/m1≡1(mod 4),所以由引理6可知,m1=1,3,5或7.
由文献[19]可知, 具有素数阶p的极大理想的有限交换局部环是Zp2和Zp[X]/(X2),它们的剩余域均为Zp,又由|R1|/m1≡1(mod 4)可知m1=1或5.
当m1=1时,R1≅Fq,q≡1(mod 4)为素数的幂.根据式(2),所以GFq是Ramanujan图.
当m1=5时,R1≅Z25或Z5[X]/(X2).此时式(2)不成立,所以GR不是Ramanujan图.
情形2s=2.
此时,式(3)等价于
若m1m2≥4或|R2|/m2≥17,则以上不等式不成立,所以GR不是Ramanujan图.
假设m1m2≤3,|R2|/m2≤16.
因为|Ri|/mi≡1(mod 4),i=1,2,所以由引理6可知m1m2=1或m1m2=3.注意到,Z9和Z3[X]/(X2)是恰有3个元素的唯一极大理想的局部环,它们的剩余域均为Z3,这与|Ri|/mi≡1(mod 4),i=1,2矛盾,所以m1m2=3不可能出现,因此m1m2=1,且以下条件之一将会出现:
(Ⅰ)R1≅R2≅F5;
(Ⅱ)R1≅R2≅F9;
(Ⅲ)R1≅R2≅F13;
(Ⅳ)R1≅F5,R2≅F9;
(Ⅴ)R1≅F5,R2≅F13;
(Ⅵ)R1≅F9,R2≅F13.
将其依次代入式(2),式(2)均不成立,所以GR不是Ramanujan图.
情形3s=3.
此时,式(3)等价于
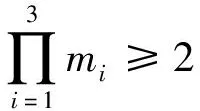
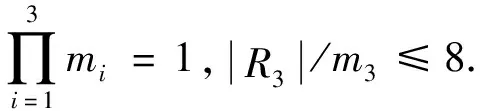
因为|Ri|/mi≡1(mod 4).i=1,2,3,所以R1≅R2≅R3≅F5,此时式(2)不成立,所以GR不是Ramanujan图.
(3)令
|λ|=
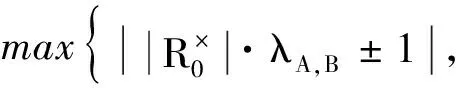
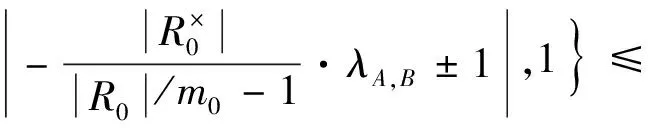
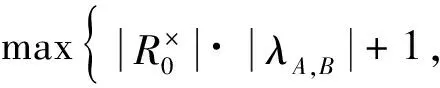

由定理4可知,GR0×R是Ramanujan图
设
μA,B=
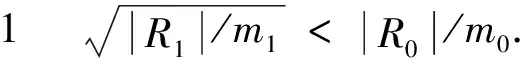
此时,GR0×R是Ramanujan图
(4)
因为
所以式(4)不成立,除非
(5)
又因为
所以当s≥3时,由式(1)可知,
即式(5)不成立,所以GR0×R不是Ramanujan图.
下面考虑1≤s≤2的情况.
子情形1.1s=1.
此时,式(5)等价于
m0m1((|R0|/m0)-1)((|R1|/m1)-1)<
若m0m1≥4或|R0|/m0≥9,则以上不等式不成立,所以GR0×R不是Ramanujan图.
假设m0m1≤3,|R0|/m0≤8.
由引理6可知m0m1=1或m0m1=3.又因为|R0|/m0≡3(mod 4),|R1|/m1≡1(mod 4),所以m0=m1=1或m0=3,m1=1.
当m0=m1=1时,R0≅F3或R0≅F7.

R0×R1≅F3×F5,F7×F5,
F7×F9,F7×F13,F7×F17,
F7×F25,F7×F29,F7×F37或F7×F41.
将其依次代入式(4)中,式(4)均不成立,所以GR0×R不是Ramanujan图.
当m0=3,m1=1时,R0≅Z9或Z3[X]/(X2).

子情形1.2s=2.
此时,式(5)等价于

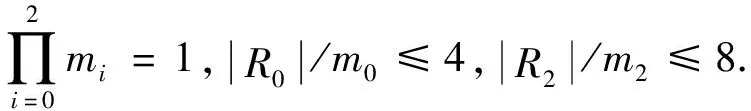
因为|R0|/m0≡3(mod 4),|Ri|/mi≡1(mod 4),i=1,2,则R0≅F3,R1≅R2≅F5,此时式(4)不成立,所以GR0×R不是Ramanujan图.
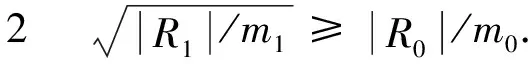
此时,GR0×R是Ramanujan图
(6)
因为
所以式(6)不成立,除非
(7)
当s≥3时,由式(1)可知,
即式(7)不成立,所以GR0×R不是Ramanujan图.
下面考虑1≤s≤2的情况.
子情形2.1s=1.
此时,式(7)等价于

8((|R0|/m0)-1).
若m0m1≥3或|R1|/m1>49,则以上不等式不成立,所以GR0×R不是Ramanujan图.
假设m0m1≤2,|R1|/m1≤49.
因为|R0|/m0≡3(mod 4),|R1|/m1≡1(mod 4),则由引理6可知,m0=m1=1.于是
R1≅F5,F9,F13,F17,F25,F29,F37,F41或F49,
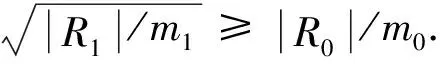
R0×R1≅F3×F9,F3×F13,F3×F17,
F3×F25,F3×F29,F3×F37,F3×F41,
F3×F49或F7×F49.
将其依次代入式(6)中,得GF3×F9是Ramanujan图.
子情形2.2s=2.
此时,式(7)等价于
4((|R0|/m0)-1)2.