三相不平衡配网下电动汽车有序充电控制策略

陈璐，王璨，胡昊，周杨俊冉，杨文涛，马鑫

（1.国网合肥供电公司，安徽 合肥 230022；2.国网安徽电力公司，安徽 合肥 230022；3.国网固原供电公司，宁夏 固原 756000）

出于对未来环境和经济的考虑，电动汽车（electric vehicle，EV）作为一个可以替代传统交通工具的交通方式在全世界范围内引起了广泛的关注。我国也在积极推动电动汽车发展，在2020年我国电动汽车的保有量将会达到500万辆[1-2]。但由于电动汽车充电时间、地点的随机性，大规模电动汽车接入电网会导致负荷峰谷差加大、电压水平下降等系列问题[3-4]。同时，电网中分布式电源的波动性和反调峰性也会进一步加重上述问题。故需对电动汽车的充电行为进行有序优化控制，以缓解上述问题并提升电网运行的安全稳定与经济性。

文献[5-6]在电网层面对电动汽车进行了有序控制研究。其中文献[5]根据每个充电站的负荷裕度生成各用户充电起始时刻的概率分布，并以此确定电动汽车起始充电时刻。该方法对削峰填谷、平抑负荷波动效果显著，但随机性较大，且电动汽车为连续充电可控性较低；文献[6]对电动汽车的充电功率进行控制，在充电负荷与常规负荷之和不高于变压器功率限制的前提下尽可能满足电动汽车充电需求。文献[7-9]在电网层面的基础上同时又考虑了用户层面。其中文献[7]建立了包含用户充电成本、充电需求满意度和负荷平稳度的多目标优化模型，并对电动汽车充电序列进行优化求解。文献[8]采用主成分分析法研究用户的出行特性，并据此对电动汽车进行有序充电控制，有效降低了负荷峰谷差。文献[9]针对居民小区存在的变压器容量越限和电动汽车缺乏管理等问题，提出了一种防止变压器过载和实现充电收益最大化的有序控制策略，有效实现了削峰填谷和降低充电成本。另外，随着可再生能源的大量并网，越来越多的文献将电动汽车与可再生能源结合考虑，用以提升可再生能源的消纳并改善配电网的电能质量。文献[10]结合电动汽车储能系统提出了一种四阶段控制方法，以降低光伏充电站、储能系统以及电动汽车充电的总成本；文献[11]针对高渗透率光伏系统，提出了一种电动汽车优化充电模型来提升光伏发电的利用率，并采用分散自治的方法来提高控制系统的效率；文献[12]结合电动汽车电池管理系统与光伏有功功率削减，来降低高渗透率光伏对配电网的影响。文献[13]提出了一种单相双向电动汽车逆变器模型（整合至智能充电桩中），该逆变器可以支持电动汽车在PQ平面的四个象限充电运行。基于该逆变器模型，若电动汽车在充电的同时通过逆变器对网络注入无功，不仅可以缓解因充电造成的电压下降、电压不平衡等问题[14-16]，同时也可降低因装设无功补偿装置而带来的投资成本，且逆变器作为电力电子器件能有效满足主动配电网快速调控的需求。

综上所述，目前研究主要存在以下2个不足：1）主要集中于对电动汽车有功进行控制，实现充电负荷的平移，未考虑电动汽车参与配电网的无功补偿控制；2）均假设电动汽车在三相平衡配电网中充电，然而，中低压配电网具有显著三相不平衡特征。基于此，本文通过分析电动汽车逆变器对配电网络的无功补偿能力，结合三相不平衡主动配电网以及分时电价，提出了一种基于逼近理想解排序方法（technique for order preference by similarity to ideal solution，TOPSIS）的三相不平衡配电网下电动汽车有序充电控制模型，该模型在满足用户充电需求与网络约束的前提下，尽可能将电动汽车安排在谷时充电；对于无法在谷时充电的电动汽车，根据其充电紧迫度进行分组优化，最大限度降低用户充电和有功/无功网络损耗的综合成本。最后通过某真实不平衡主动配电网进行案例仿真分析，验证本文所提方法的可行性与有效性。

1 电动汽车有序充电模型

1.1 电动汽车无功补偿模型

图1为各居民用户通过公共耦合点（point of common coupling，PCC）接入外部电网，对内连接家用负载、屋顶光伏和电动汽车等元件。

图1 含电动汽车用户经公共耦合点并网接线Fig.1 Residential connection with EV through PCC

公共耦合点处的有功与无功关系如下：

式中：PG，（kt），QG，（kt）分别为节点k在t时刻的电网注入有功、无功功率；PL，（kt），PPV，（kt），PPEV，（kt）分别为节点k在t时刻的居民常规有功负荷、光伏有功出力、电动汽车充电负荷；QL，（kt），QPV，（kt），QPEV，（kt）分别为节点k在t时刻的居民常规无功负荷、光伏无功出力、电动汽车无功注入。

1.2 电动汽车参数计算

1.2.1 电动汽车停留时间段数

本文对电网数据采集的时间间隔为15 min。假设第i辆电动汽车的到达时刻和离开时刻分别是，并以15 min的间隔进行取整，则其停留时间段数Tis可由下式计算得到：

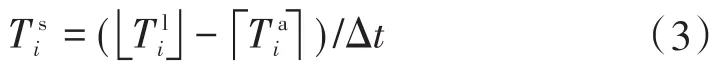
1.2.2 电动汽车返回荷电状态

本文假设电动汽车充满电后最大行驶距离dm为150 km。同时考虑对电池的保护，电动汽车一次充电的范围设定在70%[17-18]，即其荷电状态（state of charge，SOC）范围在20～90%。当荷电状态达到90%时，就认为电动汽车已充满。

1.2.3 电动汽车充电所需时段数

假设电动汽车的电池容量为EPEV：

1.2.4 电动汽车充电紧迫度

由于电网带负荷能力的限制，用电高峰期不能保证每辆电动汽车都能即来即充。为充分兼顾用户充电需求和电网运行性能，本文提出了电动汽车充电紧迫度的概念并定义如下：

1.3 充电优化控制模型

本文综合考虑电网和用户收益，旨在降低配网的网络有功损耗（fp），无功损耗（fq）和用户的充电成本（fc），同时提升电动汽车向电网输送无功功率所产生的收益（fd）。由于各目标量纲不同，故统一将各目标转换为成本的形式，目标方程定义如下：

其中

式中：Δtm为第m个时间段所用的时间；N为网络中节点总数；e(t)为分时电价；Ploss(t)，Qloss(t)分别为在t时刻的有功、无功损耗；PPpEV,k(t)，QpPEV,k(t)分别为节点k第p相的电动汽车在t时刻的有功、无功注入；c为无功电价占实际有功的百分比，本文假设即c=10%[19]。

相关约束条件有：

1）节点功率平衡方程约束：

其中

2）电压不平衡度。通常由电压不平衡系数（voltage unbalance factor，VUF）表征，并定义为电压负序分量与正序分量幅值的比值[20]：

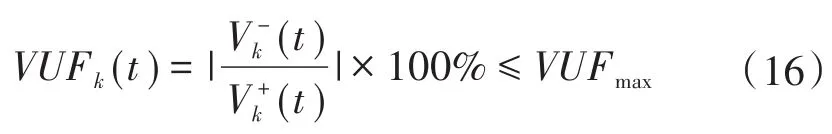
式中：VUFk（t）为三相节点k在t时刻电压不平衡系数分别为三相节点k在t时刻电压的负、正序分量；VUFmax为电压不平衡系数的上限，本文设定VUFmax=2%[21]。

3）电压幅值约束：

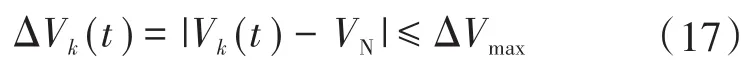
式中：ΔVk(t)为节点k在t时刻电压幅值的变化量；VN为额定电压；ΔVmax为电压幅值变化量的上限。根据仿真澳洲配网所属电网运行规范，电压幅值变化范围为±6%[22]，故本文设定ΔVmax=14.4 V（相电压额定值240 V）。

4）电动汽车荷电状态约束：

式中：SOCmax，SOCmin分别为荷电状态的上、下限。如上文所述，本文设定电动汽车荷电状态介于20～90%之间。

1.4 基于理想解法的电动汽车有序充电算法

上述电动汽车有序充电模型的目标函数为多目标函数，因此，本文采用TOPSIS算法[15]进行求解。该算法属于一种典型的多目标求解算法，具有求解速度快、灵活性好和决策效果合理的特点。本文设计的电动汽车有序充电算法流程图，如图2所示。

图2 有序充电算法整体流程图Fig.2 Flow chart of EV charging scheduling algorithm

2 电动汽车有序充电控制策略

本文基于一种单相双向电动汽车逆变器模型（整合至智能充电桩中），可以支持电动汽车在PQ平面的四个象限充电运行。

具体来说，电动汽车有序充电控制策略如下：电动汽车返回并接入充电桩后，用户设定的离开时间、电动汽车当前荷电状态和目标荷电状态等信息将自动采集至中央协调控制器，中央控制器根据上传信息确定各电动汽车充电策略。同时基于负荷水平将一天划分为3个时段，即平时（6：00～17：00）、峰时（17：00～21：00）和谷时（21：00～6：00），并对应不同电价。

由于谷时负荷电价水平较低，故优先考虑将电动汽车安排在谷时充电以实现削峰填谷、降低充电成本的效果。根据电动汽车谷时停留时段与所需充电时段的关系，有以下三种情况划分：若电动汽车谷时停留时段不小于所需充电时段，则充电时段均匀分配在谷时；若电动汽车谷时停留时段小于其所需充电时段，则其谷时停留部分全部用于充电，剩余所需充电时段在峰时和平时优化决定；若电动汽车不存在谷时停留时段（即全部在峰时或平时），则所有充电时段均由优化决定。

具体示意如图3所示，其中情况1的电动汽车所需充电时段等于停留时段，即充电紧迫度为1，即使是峰时也立即开始充电；情况2的电动汽车因在谷时停留时段大于其充电所需时段，故全部在谷时充电；情况3的电动汽车由于在谷时停留时段小于其充电所需时段，其谷时停留部分全部用于充电，剩余所需充电时段由峰时和平时优化决定；情况4的电动汽车停留时段均不在谷时，故其充电所需时段全部由优化决定。

图3 电动汽车充电策略示意图Fig.3 Schematic of proposed PEV charging strategy

对于上述情况3、情况4，部分或全部电动汽车充电时刻需通过有序优化控制确定，故本文提出如图4所示优化充电策略。

图4 电动汽车有序控制流程图Fig.4 Flow chart of coordinated charging of PEV

电动汽车充电策略具体步骤如下：

1）在任意时刻，首先检测到来与离开的车辆，计算并更新各电动汽车停留时段和充电所需时段。

2）基于各电动汽车谷时停留时段与所需充电时段，采用上述图3策略确定其充电时段，其中情况1、情况2充电时段直接确定，情况3、情况4则需优化确定。

3）情况3、情况4优化确定充电时段时，基于步骤2）判断结果进一步更新电动汽车剩余停留时段和剩余所需充电时段，并依式（9）更新此时其充电紧迫度。

4）根据充电紧迫度，通过优化确定情况3、情况4在峰时或平时的有序充电时刻。对重要度为1的电动汽车，立即进行充电；对重要度在（1，0.75]之间的电动汽车首先进行优化，根据第1.3节所提充电优化模型确定相关电动汽车充电时刻；如此依次确定剩余重要度区间的电动汽车优化充电时刻。在低重要度优化时，高重要度电动汽车充电优化结果作为已知固定条件。

5）判断是否还有下一时刻，如有则返回步骤1）。

上述步骤循环往复，直至1天24 h充电决策完成。

值得注意的是，断续充电会增加日充电次数，对电池寿命产生影响，为此本文以锂电池电动汽车为研究对象。根据文献[18]，锂电池对充电具有无记忆性优点，间歇性充电对其造成的影响可以忽略不计。而对其它类型电动汽车，为限制断续充电对电池造成的影响，可在目标函数计及电池损耗。

3 仿真验证

3.1 仿真网络

为验证本文所提基于逆变器无功能力的电动汽车有序充电控制的可行性与有效性，基于某真实配电网进行仿真分析[21]。

图5为某真实配电网415/240 V 101节点测试网络示意图。

图5 某真实配电网415/240 V 101节点测试网络Fig.5 415/240 V 101 nodes test network of one real power distribution network

图5中，该415/240 V低压配网由容量为200 kV·A、电压等级为22 kV/415 V的配电变压器供应，共有101个节点与77家用户，且各用户均装有智能电表（数据采集频率15 min每次）。其中51家用户单相接入，34家用户装有单相屋顶光伏，光伏接入情况与典型功率曲线分别如表1和图6所示。由于本文基于不平衡网络模型，故图5中位置由节点和相位共同表征，如6B代表位于6节点B相的单相节点，2代表位于2节点的三相节点。

表1 仿真网络用户及光伏接入情况Tab.1 Load and PV connections in the test network

图6 仿真网络三相日负荷曲线与光伏出力情况Fig.6 Daily load and PV profiles of the simulated network

3.2 仿真设置

根据市面电动汽车典型参数，设定电动汽车容量26 kW·h，恒定充电功率2 kW。24 h仿真时间窗口选为早晨6：00至第二天6：00。此外，光伏仅作为功率注入出现，本文不涉及光伏出力的控制，并做如下假设：

1）电动汽车为2 kW恒功率单相充电，且充电的同时向电网提供2 kvar无功注入，上述功率均满足逆变器容量限制。

2）电动汽车渗透率设为30%，共36辆电动汽车平均分布于A，B，C三相，图5中粗字体为电动汽车所在节点（三相节点处的电动汽车平均分布在三相）。

3）对应平时、峰时和谷时，采用澳大利亚真实配网所在电网的分时电价[23]，如表2所示。

表2 配电网分时电价Tab.2 Distribution time-of-use tariff

本文设置三种仿真对比案例。其中，案例1为电动汽车无序充电控制，即电动汽车到家便充电，不考虑负荷峰谷情况；案例2为不计及逆变器无功能力的电动汽车有序充电控制，即根据本文提出的有序充电控制方法仅进行有功充电管理；案例3为计及逆变器无功能力的电动汽车有序充电控制，即在案例2的基础上考虑逆变器的无功注入。

3.3 仿真结果分析

鉴于本文所定义充电优化控制模型主要涉及经济性和电网运行水平，故此处对比分析也围绕这两个方面展开。其中经济性如式（7）所示，主要含用户有功充电成本、无功注入收益和网络有功/无功损耗成本；电网运行水平如式（16）、式（17）所示，含电压幅值偏移和电压不平衡度。在电压幅值对比分析时，由于文章篇幅限制，仅选取了负荷和光伏接入最多的C相进行展示。

3.2节设置的三种方案的经济性方面对比结果如表3和图7所示。

表3 三种方案的经济性比较（$）Tab.3 Economic comparison of three cases（$）

图7 三种案例24 h有功网损曲线图Fig.7 Active network loss of three cases over 24 hours

由表3可知，在案例1电动汽车无序充电控制情况下，多数用户会在晚上下班回家后（峰时）进行充电，导致负荷峰值加重并产生高昂的充电成本61.70$和有功/无功损耗成本17.43/11.18$，累计总成本90.31$。为此采用了案例2进行电动汽车有序充电控制，由于所提策略对充电负荷进行了优化平移，在兼顾用户需求的前提下起到了削峰填谷的作用，此时总体费用降为了69.52$，其中用户充电成本和有功/无功损耗成本分别降为47.73$，13.26/8.26$，总体降幅为23.02%。

值得注意的是，如图7所示，有序充电虽降低了峰时负荷但同时加重了谷时负荷并导致谷时网损增加，这是由于案例2实现的仅是充电负荷的平移并未消除。同时案例3与案例2通过优化使得电动汽车避开了峰时充电，这也是两者峰时网损相同的原因。为了缓解上述问题，在案例2的基础上提出了计及逆变器无功能力的有序充电控制，即案例3。由图7可知，通过电动汽车逆变器的无功注入，可有效缓解有功充电负荷导致的谷时电压下降和网损上升的问题，其中用户充电成本与案例2大致相同，有功/无功损耗成本降为11.55/7.05$，考虑无功注入的收益为4.75$。总体而言，案例3的总成本较案例1降低了32.02%，为61.39$，而相比于案例2则下降了11.69%。

本文对于电压偏移量的定义为96个时间段各相电压减去额定电压后的绝对值之和的平均值，即平均每个时刻的电压偏移。

图8～图10分别为案例1～案例3中配电网C相电压仿真结果。图11～图13分别为案例1～案例3中配电网VUF仿真结果。图14为案例1～案例3电网运行水平方面仿真对比结果图。

图8 案例1配电网C相电压Fig.8 C-phase voltage of distribution network in case 1

图9 案例2配电网C相电压Fig.9 C-phase voltage of distribution network in case 2

图10 案例3配电网C相电压Fig.10 C-phase voltage of distribution network in case 3

图11 案例1配电网VUFFig.11 VUF of distribution network in case 1

图12 案例2配电网VUFFig.12 VUF of distribution network in case 2

图13 案例3配电网VUFFig.13 VUF of distribution network in case 3

图14 三种案例电网运行水平寅比Fig.14 Comparison of grid operation levels in three cases

由图14可知，在案例1无序充电情况下，电压下降和三相不平衡严重，电压偏移量为1 224 V，电压最小值为218.64 V（即电压偏移率8.90%），超出了式（17）给定的6%约束范围；电压不平衡系数最大值为2.46%，也超过了式（16）给定的2%约束。在案例2有序充电控制情况下，电压偏移量减少为1 099 V，电压最小值上升为223.53 V（即6.86%，但仍越限）；电压不平衡系数最大值下降至1.92%，满足给定约束；而案例3在引入电动汽车逆变器无功控制后，网络运行水平得到明显提升，电压偏移量下降至951 V（相比案例2降幅148 V），电压最小值上升为226.10 V（即5.79%），满足了给定6%的边界约束，且最大电压不平衡系数也进一步下降至1.44%。

通过经济性可以看出，用户充电成本在总成本中的比例最高，对电动汽车充电序列决策起到了较大影响。案例2和案例3更倾向于在低电价时进行充电以减少有功充电的成本，有功/无功损耗成本通过充电序列优化和无功补偿均不同程度降低。同时，采用本文所提电动汽车有序充电控制，电网运行水平也得到了显著提升，对提升网络负荷容量及其对光伏的消纳能力具有一定帮助。

4 结论

本文提出了一种基于逆变器无功能力的新型不平衡主动配电网电动汽车有序充电控制方法。

首先基于三相不平衡配电网模型并考虑分时电价的影响，建立了含网络有功/无功损耗成本、用户充电成本及无功注入收益的多目标优化充电模型，并采用离散粒子群优化算法和直接潮流算法进行联合求解；接着基于充电紧迫度概念并综合考虑电网运行要求和用户充电需求，提出了一种计及逆变器无功能力的电动汽车有序充电策略；最后通过对某真实配电网进行24 h仿真分析验证。

仿真结果表明：本文所提基于逆变器无功能力的不平衡主动配电网电动汽车有序充电控制方法是可行且有效的。所提方法能充分兼顾电网和用户需求，降低有功无功网损和用户充电成本，并为参与用户带来经济收益；同时利用逆变器闲置容量为电网提供无功支持，降低了充电负荷的不利影响，提升了网络负荷容量及对可再生能源的消纳能力。