含海上风电场混合直流系统的稳定下垂控制

马州生，姚阳

（1.河南经贸职业学院物联网学院，河南 郑州 450018；2.华北电力大学高压与电磁兼容北京重点实验室，北京 102206）

风能将成为电力系统中可持续发展和多元化能源投资组合的重要组成部分[1-5]。与陆上风电场相比，海上风电具有规划限制少、风速大等优点[6-8]。为了把海上风电场与陆上电网结合起来，高压直流（high-voltage direct current，HVDC）技术已被证明比交流系统更具技术、经济和环保优势[9-11]。不同拓扑结构的直流输电系统中，混合直流输电系统由在风电场侧的电压源转换器（voltage sourced converter，VSC）和并网侧的线路转换器（line-commutated converter，LCC）连接组成，因为LCC在陆地上具有更好的经济性，而VSC更适合海上安装。

利用混合高压直流系统将风能整合到电网中，需要考虑风能的间歇性特性[12]。这是因为LCC吸收无功功率进行合适的换相，HVDC系统逆变侧交流电压根据风电变化而波动。为了调节LCC在有功基准变化时所消耗的无功功率，文献[13]提出了一种直流电压调节方法，该方法在逆变侧采用了以交流电压为输入变量的比例积分（PI）控制器。文献[14]采用了一种基于整流侧和逆变侧通信的直流参考电流、电压计算方法来调节交流电压。文献[15]对文献[14]中的方法进行了改进，以适用于整流侧。然而，对于LCC高压直流系统并不适用。由于这些控制方法，整流器和逆变器的无功功率输出同时改变，故直流电压被传输线联锁。另一方面，对于HVDC系统，直流电压控制只影响LCC侧，因为VSC可以不考虑直流电压水平而调节无功功率。此外，目前的研究只考虑了提供恒定功率的HVDC系统。为了根据连续变化的有功功率调整直流电压，已有研究基于局部采集的信息研究了HVDC系统的直流电压控制方法。最广泛使用的方法是IDC/VDC下垂控制策略，它被用于多终端HVDC系统的功率分配。文献[16]提出的IDC/VDC下垂控制方法广泛用于既有VSCs又有LCCs的HVDC系统。然而，下垂控制方法仅用于混合高压直流系统的有功功率分配，很少研究其对连接交流电压的影响。为了设计不同目的的直流电压调节方法，文献[17]使用小信号模型分析了不同HVDC系统的响应特性，并利用直流电压控制器改进了LCCHVDC系统的小信号状态空间模型，以提升其瞬态响应能力。文献[18]提出的IDC/VDC下垂控制策略适用于基于VSC的多端直流系统（multi-terminal direct current，MTDC）系统的状态空间（statespace，SS）模型中。

综上所述，虽然在以往的研究中，主要针对内部控制结构和直流系统进行了大量研究，但在状态空间模型中并没有考虑直流电压调整对交流系统电压的影响。基于此，本文提出了一种IDC/VDC下垂控制方法，用于点对点海上风电场接入HVDC系统。该方法采用IDC/VDC下垂控制，利用直流电压调节抑制电网侧LCC的交流电压波动。此外，本文还给出了下垂系数的计算方法，并建立了HVDC系统的状态空间模型，采用根轨迹法对系统的稳定性进行了研究。最终，在不需要连续无功补偿装置的前提下，可实现交流电网电压不受海上风速变化的影响。

1 所提下垂控制

图1为采用下垂控制器的HVDC系统结构图。

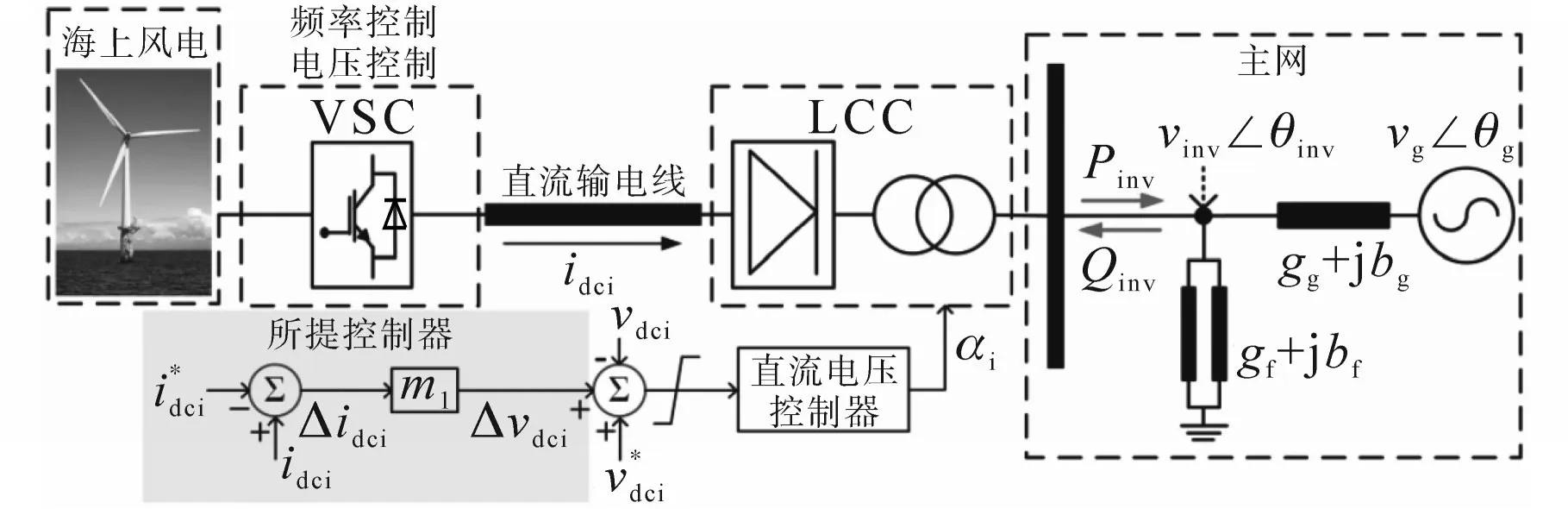
图1 采用下垂控制器的HVDC系统结构图Fig.1 Configuration of a hybrid HVDC system using the proposed droop controller

由图1可知，VSC整流器保持恒定的频率和交流电压幅值在风电侧通过高压直流输电线输送风能，LCC逆变器控制相应的直流电压参考值，并将有功功率通过直流输电线送到主网。由于采用了IDC/VDC下垂控制器，直流电压变化量Δvdci可以由直流电流偏差Δidci和下垂系数m1来确定。然而，传统方法中，无论工作点是何种情况，直流电压都是恒定的。与传统方法不同的是，当直流电压随风功率的波动而变化时，本文在逆变器侧控制器中增加了一个限幅器。此外图1中，主网采用等效电路模型来模拟交流电压特性。主网电压用vg表示，公共耦合点的电压幅值和角度可表示为vinv和θinv。等效网络导纳和滤波器导纳分别用gg+jbg和gf+jbf表示。逆变侧有功输出和无功输出分别用Pinv和Qinv表示。值得注意的是，其有功和无功的方向是相反的，这是因为LCC具有吸收无功功率的特性。本文所提控制器的目标是通过调节直流电压来减小有功功率变化时交流电压的波动。所提控制器由下垂系数计算器和内部直流控制器两部分组成。计算器推导出最佳下垂系数m1，保持交流电压不变，计算器采用直流电压、电流设定点和电网等效导纳的数据。无论输出有功功率怎样变化，直流电流设定点为1（标幺值），其值由预测风电功率确定：

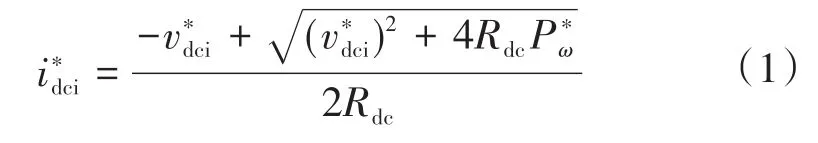
式中：Rdc为直流输电线的电阻。

其中

另一方面，利用LCC的特征方程，Pinv和Qinv也可以用高压直流系统参数表示为

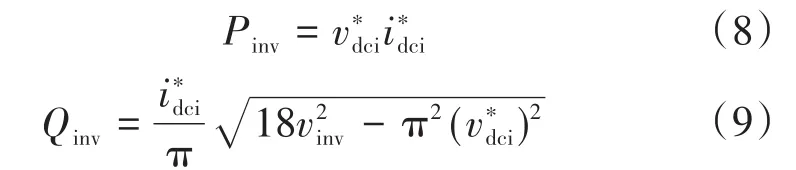
此处没有出现匝数比，因为系统是按单位（标幺值）设计的。将式（8）和式（9）代入式（4），则vinv可以用表示。因此，由一阶泰勒近似，可确定电压偏差Δvinv为

由于直流电压的偏差是m1与直流电流的偏差Δidci的乘积，因此，为了保持交流电压恒定时的最佳下垂系数可推导为

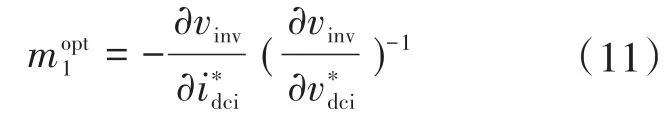
式（11）中使用的导数可以通过求导式（4）、式（8）和式（9）得出：

由于直流电压不能超过稳定运行的最小和最大边界，因此，可以定义本文允许的最大有功波动。直流电压约束可以描述为

对于VSC和LCC，风能ΔPω的波动可以用逆变侧有功功率ΔPinv和直流线路损耗表示为

其中，ΔPinv可以用泰勒近似定义为

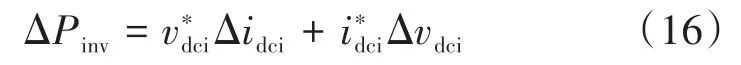
利用式（16），可将ΔPω改写为

将式（14）中的Δvdci代入式（17），可由最大与最小有功功率之差定义可接受的最大风电波动ΔPmax为

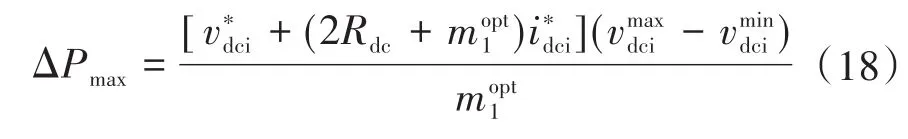
综上所述，利用所提出的控制策略，可以在没有交流电压波动的情况下，适应小于ΔPmax的海上风电功率的变化。在高压直流系统中进行直流电压调整时，必须考虑直流电缆的要求。因此，该方法不会对直流电缆的性能造成显著的影响。

2 系统模型与稳定性分析

为了研究运行点附近的稳定性，本文建立了一个混合高压直流系统的状态空间模型，其中，风电场分别用注入整流站的母线、ΔPω和ΔQω表示。图2为整流侧的交流电路图和控制结构图。本文将电压和电流有关的变量都转换到d，q轴上进行表示。

图2 整流侧的配置Fig.2 Configuration of the rectifier side

图2a中输出电压、电流分别为Δvsd+jΔvsq，Δisd+jΔisq。变流器侧电压、电流分别为Δvcd+jΔvcq，Δicd+jΔicq。整流母线与 VSC 之间的电阻和电感分别用Rc和Lc表示。将谐波滤波器建模为单个电容Cf，由图2a可知风电场ΔPω和ΔQω可表示为

图2b为VSC的控制方框图。控制器的目的是调节相应基准处的输出电压。电压控制器的PI增益分别描述为Kpr和Kir。电流控制器的PI增益描述为Kpc和Kic。为了将所提控制结构表示为状态空间模型。在d，q轴上引入了额外的状态（Δud和Δuq）。由图2b可知，引入的变量Δud和Δuq的时间导数可表示为

式中：x∈{d,q}；s为状态变量。

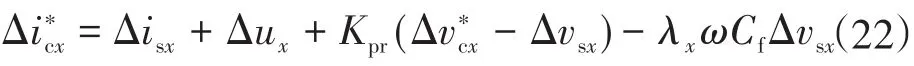
其中，λx=1，x=d；λx=-1，x=q。

式中：ω为系统角频率。

式中：Aω为系统状态系数矩阵；Bω为系统控制系数矩阵。

在图2a中，传递给直流系统的有功功率ΔPdcr可定义为

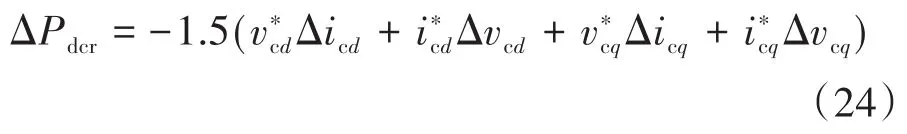
本文输电线采用T线模型。VSC的等效电容用Ceq表示。线路电阻、电感、电容用Rdc，Ldc和Cdc表示。平滑电抗器的电感用Ls表示。直流系统的输入变量为风电场传递的有功功率ΔPdcr，定义为

式中：Δidcc为传输线中点直流电流，其动力学方程为

式中：Δvdcc为传输线中点直流电压，其动力学方程为

其动态方程为

式中：Linv为逆变侧的电感。

LCC模型的方程为

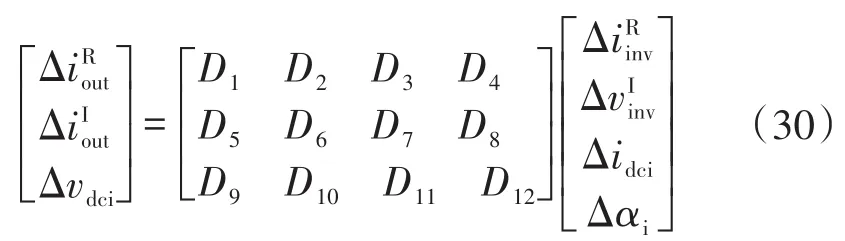
式中：Kpi和Kii为直流稳压器的PI增益。

引入一个附加的状态变量Δxi到PI控制器。将式（29）和式（31）中的Δαi代入式（30），Δxi的动力学方程可以表示为

因此，直流系统的状态空间模型由状态矢量ΔX1=[ΔvdcrΔidcrΔxiΔidciΔvdcc]T和 输 入 向 量可以表示为

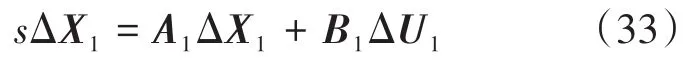
图3为上述完整模型的根轨迹图，以研究Ls，Ceq，（Kpr，Kpi）和（Kir，Kii）的变化对小信号稳定性的影响。

图3 所提方法的根轨迹图Fig.3 The root locus diagram of the proposed method

如图 3 所示，Ls，Ceq，（Kpr，Kpi）和（Kir，Kii）分别从 0增加到 0.002；0.002 5增加到 0.1；（0.1，0.063）增加到（10，6.3）；（10，4.13）增加到（1 000，413），其中，上述变量单位都为（标幺值）。根轨迹分析在额定风力下进行，Pω=1（标幺值）。所有极点的轨迹都在左平面。即采用该方法对混合高压直流系统进行控制，可以保证混合高压直流系统在额定功率下稳定运行。

为说明所提方法在不同运行工况下是稳定的，风电场变化的根轨迹分析如图4所示。为了确定m1的范围，假设直流电压的变化与电流的变化方向相同，直流电流的变化幅度大于直流电压的变化幅度。由图4可知，不管运行条件和m1的变化，所有极点都位于左半平面。因此，所提出的方法在大范围运行条件下是稳定的。此外，当m1增大时，主极远离虚轴，当m1较大时，直流系统达到稳态工作点的速度更快。

图4 随m1的增加本文方法的根轨迹图Fig.4 The root locus diagram of the proposed method as m1increases

3 仿真分析

通过仿真，与传统法进行比较，以验证所提方法的有效性和优越性。由于状态空间模型是基于工作点附近的线性化参数，两个模型的响应相似。传统法是指不管有功功率的变化，直流电压都是恒定的方法。

仿真系统相关参数设置如下：Rc=1.89×10-5，Lc=4.72×10-5，Cf=7.935×10-5，Kpr=1，Kir=100，Rdc=0.02，Cdc=0.01，Kpi=0.63，Kii=41.3，gg=0.64，gf=0.014，τi=1×10-4，P*ω=1.0，Q*ω=0，Ceq=0.012 5，Ls=0.002，Ldc=2×10-4，vg=0.935 0，bg=-2.41，bf=0.5。以上变量单位均为标幺值。

3.1 阶跃响应比较

图5比较了传统方法与本文方法的混合高压直流系统的Pinv，vdci和vinv阶跃响应。m1的值为0.400，1。在t=2 s时，风电场的有功功率Pω从1（标幺值）减小到0.9（标幺值），根据风电的变化，逆变侧的有功功率Pinv从0.98（标幺值）减小到0.88（标幺值）。

图5 采用传统和本文方法的HVDC寅风力阶跃变化的响应Fig.5 The responses of the hybrid HVDC systems for a step change in wind power using the conventional and proposed methods

由图5可知，对于有功功率变化，传统方法可保持不变。利用Ipc/Vpc下垂控制器，对于所提出的策略，vinv保持不变，传统方法则在增加。两种方法之间的vinv差异明显，微分Diffv为0.02（标幺值）。这说明该控制器有效抑制了风力发电阶跃变化时的电压偏差。

由图5的放大图可知，PSCAD模型和式（33）SS模型的响应几乎完全相同，这是因为简化了网格阻抗、忽略了快速动态特性。

3.2 根据下垂系数的连续响应

图6为HVDC状态空间模型在m1分别为0，0.2，0.439 4（最优值）和0.7四种不同值时的响应情况。由图6可知，无论m1如何变化，HVDC的输出有功功率都是相同的，这就意味着m1对有功功率的影响可以忽略不计。随着m1的增大，直流电压变化更快。然而，当m1为最优值时，交流电压波动受到的抑制效果最为明显。结果表明，在m1未达到最优值的情况下，与传统的m1=0时相比，交流电压的抑制效果更好。在m1=0.439 4时，Vinv的变化幅度仅为0.4%。在最优设置下，最大和最小有功功率之差为0.16（标幺值）。直流电压变化是0.05（标幺值）。这意味着通过改变直流电压的5%，可保持交流电压能在16%的有功功率波动下不变。

图6 采用本文方法的HVDC随m1连续变化的响应Fig.6 Continuous responses of the hybrid HVDC systems using the proposed method with variation in m1

3.3 模型线性特性的影响

图7为采用传统方法和本文方法控制的HVDC的阶跃响应。当风电功率从0.9（标幺值）降至0.5（标幺值）时，由于采用基于下垂的控制器必然存在线性化限制，当存在较大扰动时，交流电压可能无法保持恒定。在评估所提出的方法时，本案例验证线性化误差对交流电压无影响。

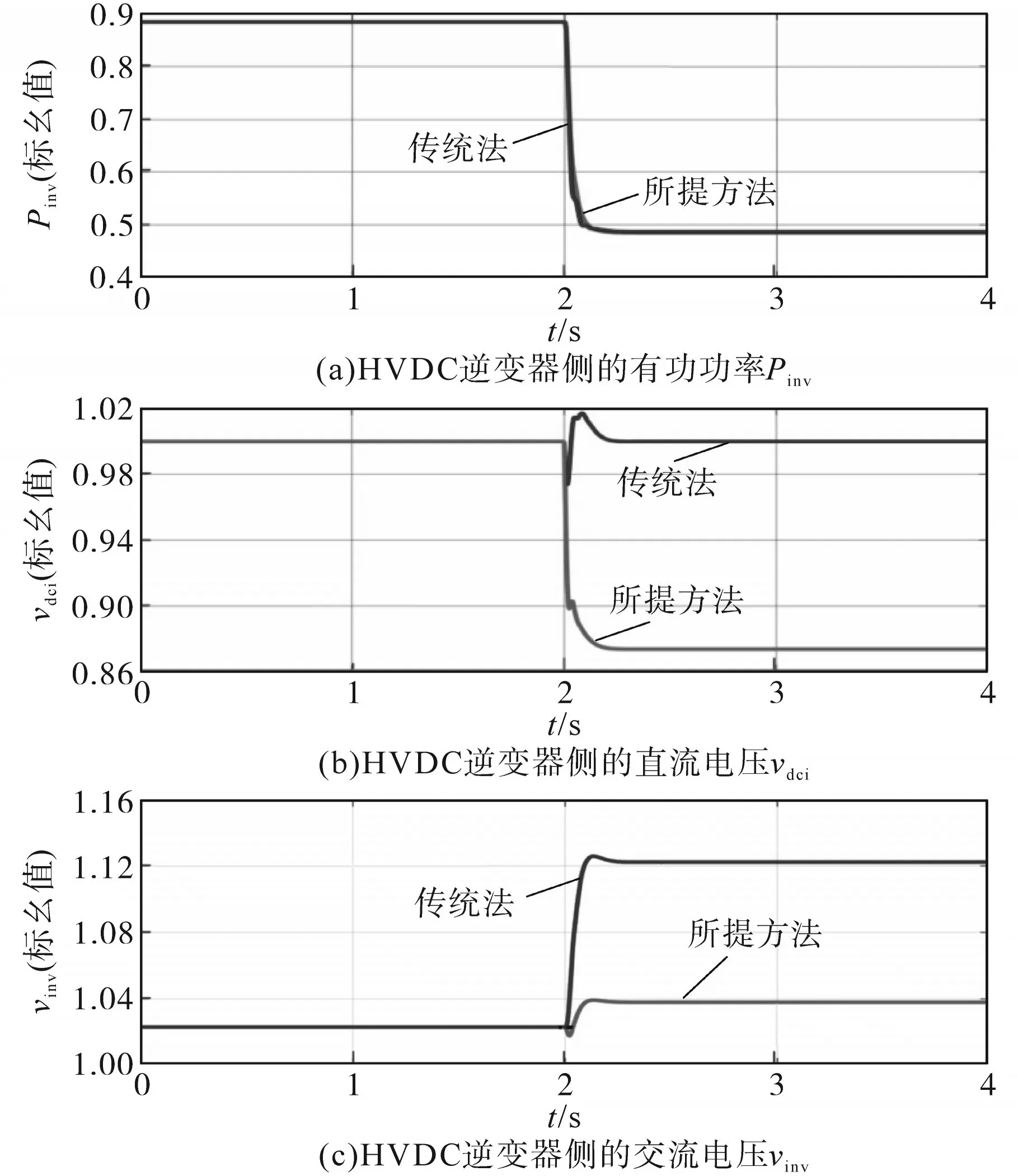
图7 ΔPω=-0.4（标幺值）的阶跃响应Fig.7 Step responses for ΔPω =-0.4（标幺值）

如图7所示，两种方法的有功功率响应基本相同。由于没有施加下边界，直流电压下降到0.87（标幺值）。考虑到控制器的线性特性，在采用该方法的情况下，交流电压从1.02（标幺值）增加到1.04（标幺值）。然而，使用传统方法，交流电压上升10%。因此，尽管在较大的扰动下，下垂控制与线性化误差相关，但与传统方法相比，交流电压得到了有效的保持。

4 结论

为了在无通信的情况下保持风电变化过程中交流电压的波动在允许范围内，本文提出了一种适用于含海上风电场HVDC的Ipc/Vpc下垂控制方法。首先，给出了最优下垂系数的计算方法，并提出了验证最大有功波动量的指导方针。此外，还提出了一个HVDC的状态空间模型，并采用根轨迹法分析其稳定性。仿真结果表明，该方法能有效地抑制风力发电对交流电压的影响，验证所提方法的有效性和优越性。