基于改进粒子群算法的并网逆变器分数阶PIλDμ控制研究

谢玲玲，陆柳，刘斌

(广西大学 电气工程学院，南宁 530004)

0 引 言

绝大多数的可再生能源是以逆变器作为并网接口，并网逆变器是可再生能源发电单元、公共电网以及本地负载之间的能量转换接口装置，承担着分布式发电(Distributed Generation，DG)系统能量的转换与控制，其性能好坏直接决定着并网电流质量，对DG的安全、稳定和高质量运行十分重要[1]。LCL滤波器为三阶系统，存在高频谐振峰，将其应用于并网逆变器电流滤波时，该谐振峰容易导致逆变器系统失稳。当电网发生扰动时，采用整数阶PID控制器的并网逆变器抑制电网谐波的能力不足，降低电能质量[2-3]。因此，为提高并网逆变器系统的谐波抑制能力，增强稳定性和快速动态调节能力，研究并网逆变器高效可靠的控制策略具有重要的理论和实际工程意义。

整数阶PID控制器结构简单，易于操作，在并网逆变器控制中得到了广泛的应用。文献[4]提出了一种电压型逆变器自适应PID控制方法，通过在传统PID控制基础上，增加3个控制项来提高系统鲁棒性，但该自适应控制方法对系统增益的调整有限，同时增加了系统设计的复杂性。文献[5-6]在PID控制方法的基础上提出自适应比例谐振微分(PRD)控制方法，实现了对参考信号的零稳态误差跟踪，提高了系统的动态响应性能，改善了并网电能质量，通过对传统整数阶PID控制方法进行改进，在一定程度上改善了系统性能，但因参数选择的局限性，PID控制器的稳定范围仍受限，致使控制系统性能欠佳。

随着非线性控制理论的迅速发展，非线性控制方法在电力电子变换器中的应用愈加广泛。Podlubny教授在1999年提出了分数阶PIλDμ控制器，在传统PID控制器的基础上引入了两个可调参数：积分阶次λ、微分阶次μ，与整数阶PID控制器相比，分数阶PIλDμ控制器的控制效果更具柔性，控制范围也从点状网格扩展到面状[7-9]。目前分数阶PIλDμ控制已在化工、电力、机械、自动化等领域中得到了应用。文献[10-12]给出了分数阶PIλDμ控制器的设计方法及其参数整定方法，将该控制器应用于简单控制系统中，并与传统整数阶PID控制效果进行比较，结果表明分数阶PIλDμ控制器能获得比传统PID控制器更快速的动态响应，其控制效果更显著。文献[13-14]针对光伏并网逆变器及其最大功率点追踪，提出并设计一种基于能量整形的无源分数阶PIλDμ控制器，算例仿真结果表明，该控制器在各种大气条件下均能获得最满意的控制性能，且总体控制成本最低。

提出一种基于改进粒子群算法(Modified Particle Swarm Optimization Algorithm，MPSO)的并网逆变器分数阶PIλDμ控制策略，相比于传统PID控制器，PIλDμ控制器的可调参数变多，可更加灵活地控制被控对象。粒子群算法经改进后可进一步提高局部搜索收敛速度，使控制器参数寻优的效率与精度更高。文章首先分析分数阶PIλDμ控制器参数λ、μ对被控系统稳定性的影响；其次建立并网逆变器数学模型，在此基础上提出基于分数阶PIλDμ控制器的并网逆变器控制策略，并与整数阶PID控制进行比较；最后采用MPSO算法对分数阶PIλDμ控制器进行参数寻优，使参数随外界环境的变化而自动调整。仿真结果验证了理论分析的正确性。

1 分数阶PIλDμ控制器

分数阶PIλDμ控制器结构框图如图1所示。其中，Kp为比例系数，Ki为积分系数，Kd为微分系数，λ为积分阶次，μ为微分阶次。

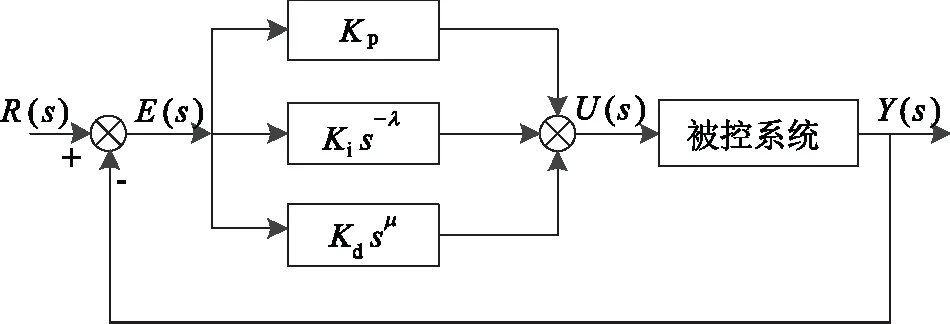
图1 分数阶PIλDμ控制系统结构框图

由图1可得，分数阶PIλDμ控制器的传递函数为：

(1)

式中 积分阶次λ与微分阶次μ分别满足0<λ<2、 0<μ<2。时域下，控制器输出U(s)表达式为：

u(t)=Kpe(t)+KiD-λe(t)+KdD-μe(t)

(2)

由式(1)、式(2)可知，当λ=μ=0时，为P控制器；当λ=1,μ=0时，为PI控制器；当λ=0,μ=1时，为PD控制器；λ=μ=1时，为PID控制器。

引入积分阶次λ和微分阶次μ使得分数阶PIλDμ控制器参数的取值更加灵活多变。图2所为控制系统在不同积分、微分阶次下的伯德图。

由图2可知通过改变分数阶PIλDμ控制器中的积分阶次λ和微分阶次μ的值可改善系统的稳态误差与动态特性。

图2 不同积分、微分阶次下的伯德图

2 基于分数阶PIλDμ控制的单相LCL并网逆变器系统

2.1 并网逆变器系统数学模型

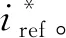
图3 系统控制示意图

并网逆变器系统控制框图如图4所示。当开关频率足够高时，逆变桥等效为比例环节，Kpwm=Udc/Uca，其中Uca为三角载波的幅值。

图4 系统控制策略框图

D1(s)=H1KpwmGC(s)+(L1+L2+Lg)s+

H2C(L2+Lg)Kpwns2+CL1(L2+Lg)s3

(3)

(4)

在只考虑ug输入的情况下，系统的传递函数为：

(5)

则系统输出并网电流i2的表达式为：

(6)

因此，要使并网电流不受电网电压影响，应满足：

G2(s)ug(s)=0

(7)

将式(5)代入式(7)得传递函数A的表达式为：

(8)

当A满足式(7)时，系统可完全消除电网电压对并网电流的影响。

2.2 并网逆变器系统稳定性分析

整数阶PID控制的系统具有有限维的特点，而分数阶系统可实现无限维控制，因此直接求解分数阶微积分方程具有较大的困难[15]。采用改进型Oustaloup滤波算法对分数阶微分算子进行拟合。改进的Oustaloup滤波器的数学模型为[16]：

(9)

式(9)中相关变量的说明如下：

(10)

式中ωh为划定频段上限；ωb为划定频段下限；b=10,d=9。

由图4可得系统开环传递函数为：

(11)

当系统控制器为整数阶PID时，Gc(s)为PID控制器传递函数；当系统控制器为分数阶PIλDμ时，Gc(s)为PIλDμ控制器传递函数。由式(9)可得系统采用整数阶PID与分数阶PIλDμ控制器的伯德图如图5所示。

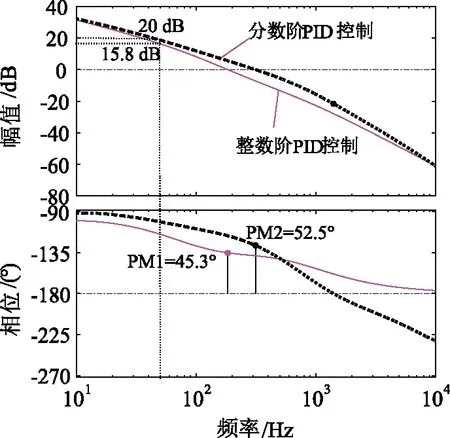
图5 不同控制策略下的系统伯德图

由图5可知，采用整数阶PID控制时系统在基频处的增益为15.8 dB，系统相位裕度为45.3°；当采用分数阶PIλDμ控制时，系统在基频处的增益为20 dB，系统相位裕度提高到了52.5°，分数阶PIλDμ控制时，系统基频增益与相位裕度均有所提高，且系统在高频段对谐波的衰减能力更强。显然，系统在采用分数阶PIλDμ控制时，其动态响应速度与谐波衰减能力均有所改善。

3 基于分数阶PIλDμ控制器参数取值范围与寻优

3.1 Ki与λ的取值范围

当Kp=50、Kd=0.05、Ki=6 000、μ=0.9，λ从0.5变化到1.3时，开环系统奈氏图如图6所示。由图6可以看出,当积分阶次λ<1时，λ越大，系统相位裕度随之增大；当λ>1时，λ的变化对系统稳定性几乎无影响。

图6 λ=0.5～1.3对应系统奈氏图

当Kp=50、Kd=0.05、μ=0.9，λ从0.7变化到1.3，Ki从600变化到1 000时，开环系统的奈氏图如图7所示。

图7 Ki=6000～10000, λ=0.7～1.3对应开环系统奈氏图

由图7可知，当λ<1时Ki越小，系统相位裕度随之增大，但仍小于40°；当λ>1时，Ki的变化对系统稳定性几乎无影响。为保证系统相位裕度γ>40°，应选取1<λ<2；Ki的值可根据实际情况选取。

3.2 Kp、Kd与μ的取值范围

文中所研究的单相LCL并网逆变器系统为Ⅱ型系统，当μ>1时，开环系统在右半平面有一个极点，但开环系统奈氏曲线逆时针、顺时针包围(-1，j0)点各一圈，故闭环系统不稳定。当Kp=50、Kd=0.05，μ从0.5变化到1.3时开环系统奈氏图如图8所示。由图8可知当μ<1时，随着μ增大，系统相位裕度和增益裕度也会逐渐增大。

图8 Kp= 50、Kd =0.05对应开环系统奈氏图

当Ki=6 800、λ=1.3、μ=0.9，Kp从30变化到80，Kd从0.05变化到0.5时，开环系统奈氏图如图9所示。表1为μ=0.9时，Kp、Kd对应的系统相位裕度与增益裕度的值。

图9 μ=0.9对应的开环系统奈氏图

由图9与表1数据可知，当Kp增大时，系统相位裕度与增益裕度均呈下降趋势；当Kd从0.05增大到0.1时，相位裕度增加了14.5°，Kd继续增大，相位裕度反而显著下降，增益裕度则随着Kd的增大持续下降。因此，为保证系统有足够的稳定裕度，μ的取值应不大于1；Kp应不大于80，同时考虑到系统的鲁棒性，Kd应不大于0.5。

表1 μ=0.9时，Kp、Kd对应系统稳定裕度的值

3.3 基于改进粒子群算法的分数阶PIλDμ控制器的参数寻优

为了克服手动调节参数的不确定性和繁琐性，降低分数阶控制器解析设计的复杂性，采用改进粒子群(Modified Particle Swarm Optimization, MPSO)算法对分数阶PIλDμ控制器进行参数寻优，从而提高控制器参数的自适应性。

将分数阶控制器PIλDμ的参数Kp、Ki、Kd、λ、μ作为1个粒子的5个维度，在五维空间中对参数进行寻优计算[17]。粒子i在第t+1次迭代计算时的速度和位置根据以下公式进行更新[18]：

Vin(t+1)=w(t+1)Vin(t)+c1r1(Pin(t)-Xin(t))+c2r2(Pgn(t)-Xin(t))

(12)

Xin(t+1)=Xin(t)+Vin(t+1)

(13)

式中Vin和Xin为第i个粒子的速度与位置。其中，1≤n≤N,N为搜索值域的维数，w为惯性权重，c1和c2为粒子加速系数，r1、r2是两个独立的随机数，介于[0,1]之间，c1r1和c2r2控制整个粒子群的运动速度。Pi为第i个粒子当前的最佳位置，Pg为粒子群目前的最佳位置。Xin∈[Xmin，Xmax]，粒子的取值范围由当前具体问题决定，Vin∈[Vmin，Vmax]，单步前进最大速度Vmax是根据粒子的取值范围来确定的，可以用来限制粒子单步迭代的最大速度。

为保证粒子群不陷入局部最优解，在每一次的迭代过程当中，都更新粒子群的动态。因此在基本粒子群算法上对粒子群的惯性权值进行改进，使其随迭代次数的增加而线性下降，以实现在算法搜索前期能加强全局搜索能力，扩大搜索空间，而当算法迭代次数增多后，则缩小搜索范围，围绕粒子当前位置进行局部搜索，增强算法收敛性，提高算法精度。改进的惯性权值的计算公式为[19]:

(14)

式中w(k)为粒子群在第k代时的惯性权值；wmax、wmin分别代表权重取值区间的上、下限；t为当前所处进化代数，Iter为算法设定进化代数的上限。

在参数寻优过程中，选择ITAE指标作为适应度函数[20]，e(t)为系统误差，J的值越小表示系统控制性能越好：

(15)

改进粒子群算法的流程如图10、图11所示。

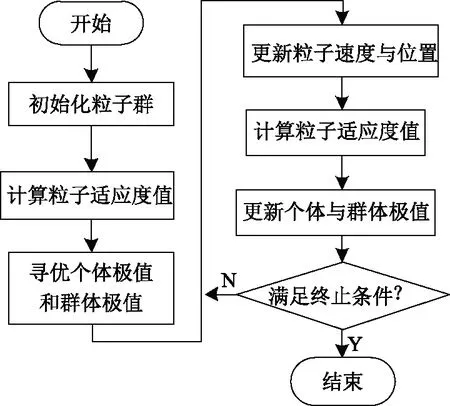
图10 改进粒子群算法流程图

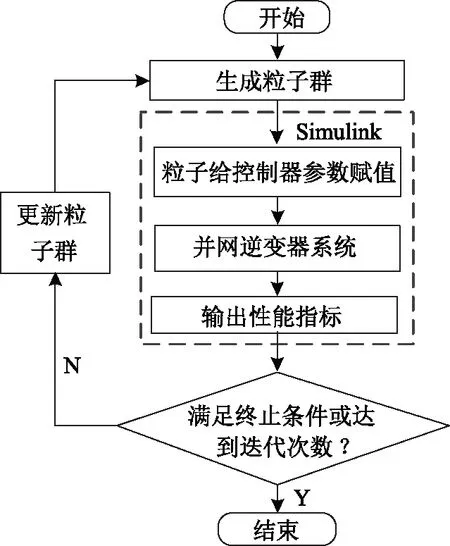
图11 MPSO优化控制器流程图

优化过程中，粒子和其所对应仿真模型的输出值作为Simulink仿真模型与MPSO算法之间的桥梁。

使用MPSO算法优化分数阶PIλDμ控制器的系统伯德图如图12所示，图12中对应的系统各项指标如表2所示。

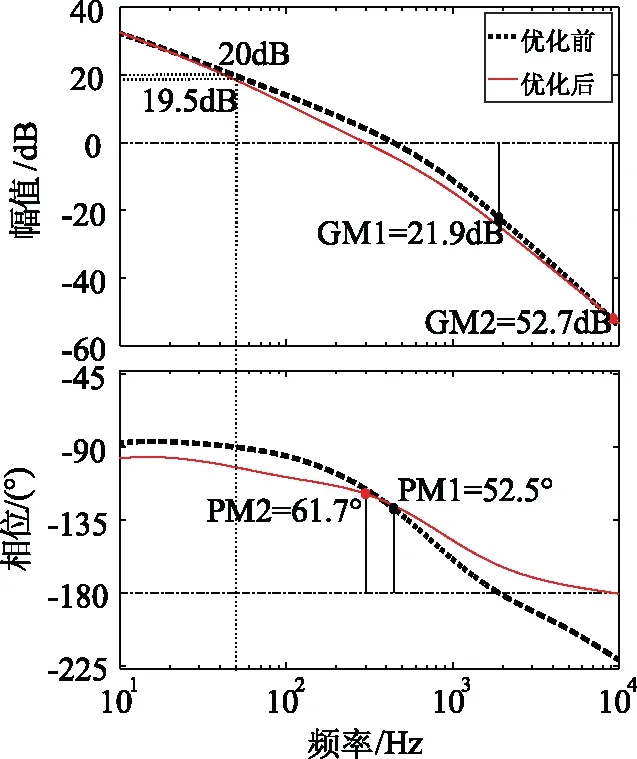
图12 MPSO算法优化PIλDμ控制器的系统伯德图

表2 MPSO算法优化分数阶PIλDμ控制器前后系统各指标

由表2可知，使用MPSO算法优化分数阶PIλDμ控制器，虽然系统的基频增益下降了0.5 dB，但大大提高了系统增益裕度和相位裕度。因此，MPSO算法优化分数阶PIλDμ控制器可改善系统动态与稳态性能。

4 仿真结果分析

为验证上述控制方法的有效性，在Simulink平台上搭建单相LCL并网逆变器系统模型。仿真参数如表3所示。

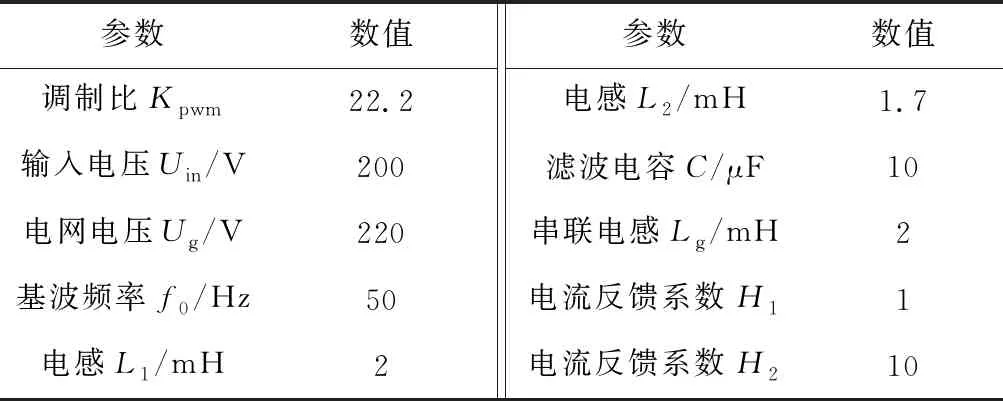
表3 仿真参数

在实际应用中，电网存在着一定量的高频谐波，因此在仿真过程中向电网ug掺入11次、13次、15次谐波分量。

电网含11次、13次、15次谐波分量时仿真波形如图13所示。可以看出，采用传统整数阶PID控制时，并网电流受电压质量的影响较大，电流波形正弦性良好但却不光滑，高次谐波含量较大；采用基于MPSO算法的分数阶PIλDμ控制器时，并网电流波形正弦性好且光滑，更好地消除了电网中的谐波影响。

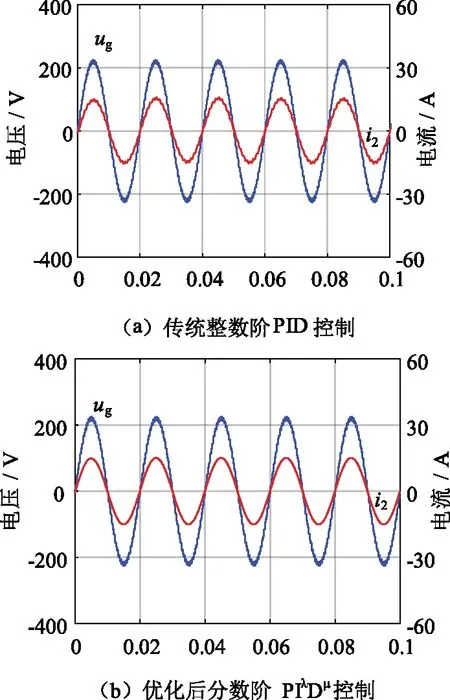
图13 电网含11次、13次、15次谐波分量时仿真波形

不同控制下并网电流的谐波含量分析如图14所示。

图14 不同控制下并网电流的谐波含量分析

由图14可知，传统整数阶PID控制下的并网电流谐波含量为3.35%，分数阶PIλDμ控制下并网电流的谐波含量为0.49%，电流谐波含量明显降低。

不同控制下电流突减仿真波形如图15所示。从图15(a)可知，传统整数阶PID控制下电流在0.04 s从15.08 A突减至7.08 A，经过0.002 1 s后电流恢复；从图15(b)可知，分数阶PIλDμ控制下电流在0.04 s从15.08 A突减至7.08 A，经过0.001 2 s后电流恢复稳定。

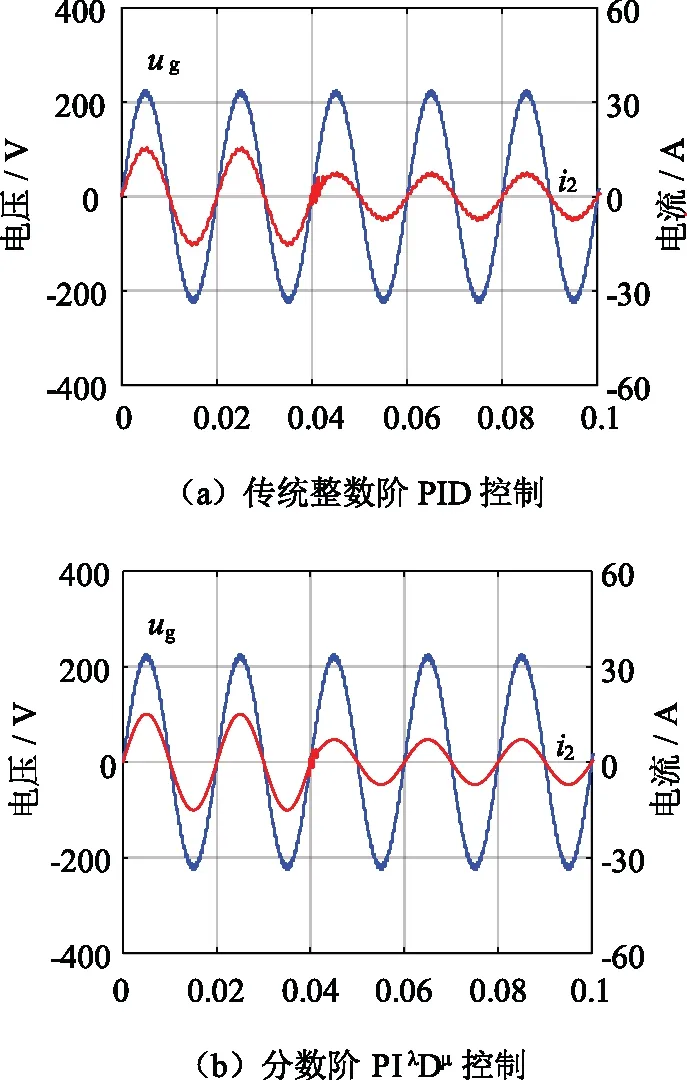
图15 不同控制下电流突减仿真波形

不同控制下电流突增仿真波形如图16所示。由图16(a)可知，传统整数阶PID控制下电流在0.04 s从15.08 A突增至23.08 A，经过0.002 2 s后电流恢复；由图16(b)可知，分数阶PIλDμ控制下，电流在0.04 s从15.08 A突增至23.08 A，经过0.001 2 s后电流恢复稳定。分数阶PIλDμ控制下电流突变时系统均能更快速的恢复稳定，因此采用分数阶PIλDμ控制器，可大大提高并网逆变器动态响应。

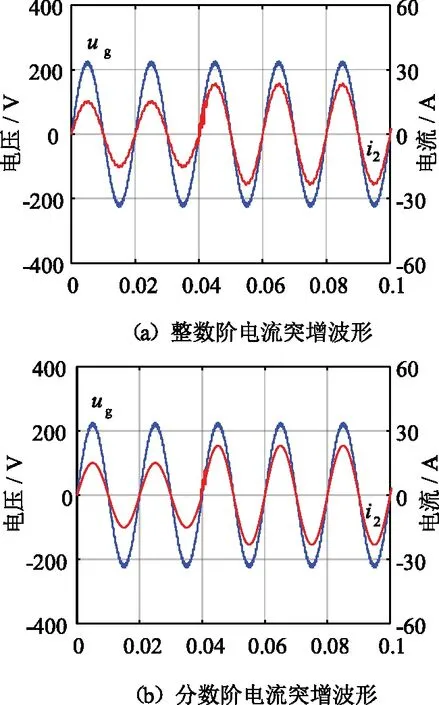
图16 不同控制下电流突增仿真波形

以电网电压突降作为外部扰动，分数阶PIλDμ控制下，电网电压在0.045 s时，电压突降20%，从220 V跌落至176 V。外部扰动下入网电流的波形和谐波含量分析分别如图17、图18所示。

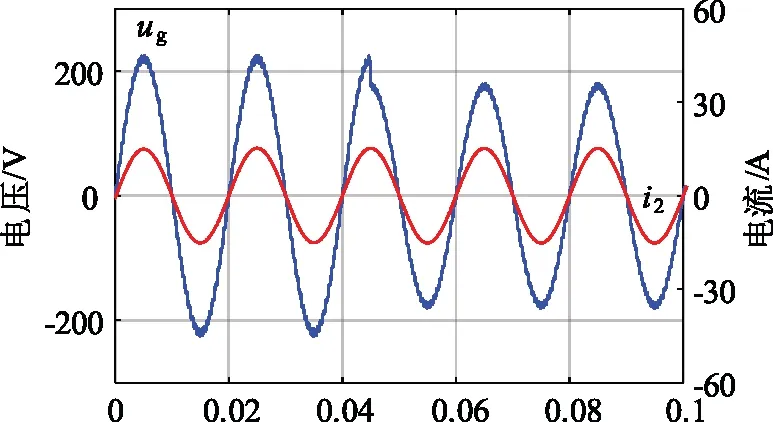
图17 外部扰动下入网电流的波形

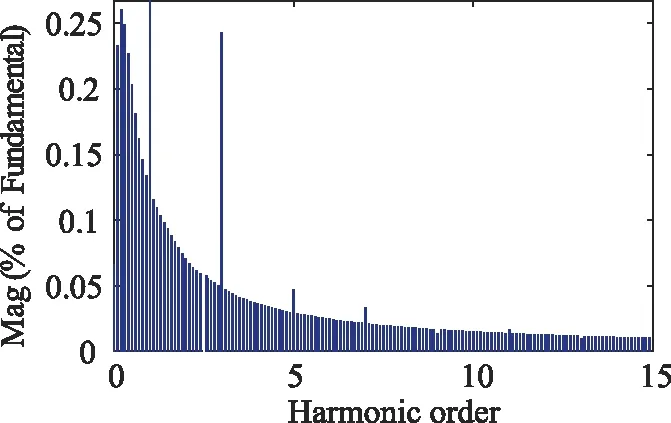
图18 外部扰动下入网电流谐波含量分析

从图17可知，入网电流波形良好，与图12(b)对比无变化。

从图18可知，在分数阶PIλDμ控制下，入网电流THD值为0.67%，对比图14(b)，THD值虽增加了0.18%，但仍在标准要求的范围内，证明分数阶PIλDμ控制能够良好抑制电网电压跌落、谐波等外部扰动。

5 结束语

文章对基于改进粒子群算法的单相LCL并网逆变器分数阶PIλDμ控制系统进行了深入的研究，详细分析了λ、μ对系统控制性能以及Kp、Ki、Kd稳定范围的影响：当λ、μ≤1时，λ、μ增大时，Kd的稳定范围与系统稳定裕度随之增大，系统抗干扰性增强，但响应速度也随之下降；相反，λ、μ减小时，系统相位裕度下降，若λ、μ的值过小，容易造成系统震荡，甚至不稳定；当1<λ<2时，其值的变化对系统性能基本无影响，但当μ>1时，系统失稳。将分数阶PIλDμ控制器与电流双闭环、网压前馈控制相结合，使得入网电流THD值下降到标准规定的0.5%以下，且系统受到外部扰动时，分数阶PIλDμ控制能很好抑制干扰，仍可保证入网电流THD值低于1%，大大提高了电能质量。采用改进粒子群算法对分数阶PIλDμ控制器进行参数整定，在控制过程中实现参数自动寻优，进一步提高系统的效率和控制性能。仿真验证了所提控制策略的有效性。