基于改进型自适应滤波器的正负序分解方法

张振，任旭虎，张圣坤

(中国石油大学(华东) 海洋与空间信息学院，山东 青岛 266580)

0 引 言

为改善供电系统中三相电压不平衡时的控制问题，需要对电网电压进行正负序分量分离 ，实现对正负序分量的单独控制。电网中由于非线性负载的存在，导致电网中三相电压不平衡[1-2]的现象时有发生。因此，三相电压不平衡条件下的正负序分量提取成为了亟需解决的问题，针对正负序分量的提取，国内外的研究者提出了很多方法。

电网电压正负序提取的技术主要是α-β参考坐标系或d-q同步旋转坐标系[3-4]、锁相环[5](Phase Locked Loop, PLL)。通过锁相环与坐标系的变换结合，实现电网电压正负序分量的提取。但是，正负序分量的提取要求锁相环具有更小的带宽，因此具有比基本同步参考坐标系[6-7](Synchronous Reference Frame PLL, SRF-PLL)更复杂的结构。为在不平衡和故障运行条件下获得更强大的同步方案，提出了解耦双同步参考坐标系锁相环[8](Decoupled Double Synchronous Reference Frame PLL, DDSRF-PLL)的结构，该方法利用坐标变换和解耦网络将三相电网电压的正负序分量进行分离，但算法结构复杂，运算过程较慢。在分析对称向量法(Method of Symmetrical Components, MSC)及单相同步锁相环的基础上，提出一种双二阶广义积分器锁相环[9-10](Dual Second Order Generalized Integrator PLL, DSOGI-PLL)的解决方案，用两个SOGI单元，产生两组正交信号，通过正负序计算单元，提取出基波中的正负序分量。后来，在此基础上发展出双二阶广义积分器锁频环[11](Dual Second Order Generalized Integrator FLL, DSOGI-FLL)的方法，使用锁频环代替传统的锁相环，但以上两种基于二阶广义积分器的同步方案中未考虑输入信号的波动情况，受输入信号的影响大，算法精度低。

文中在对自适应陷波器[12](Adaptive Notch Filter, ANF)进行理论分析的基础上，优化ANF的结构，将基波的频率和幅值的估计值引入ANF的结构中，使ANF的响应具有幅值和频率的自适应性，与传统的ANF算法相比，能减少频率跳变和幅值变化对频率动态响应的影响。而后将改进后的ANF结构用于并网控制的正负序分量提取中，仿真结果表明改进后的ANF结构较传统的ANF结构提取出的正负序分量的波动更小，能够很好地抑制电网不平衡条件下频率跳变和幅值变化的影响。同时，仿真结果验证了改进ANF结构用于正负序分量提取的性能优势。

1 自适应滤波陷波器

全局收敛的自适应滤波器，由一个二阶滤波器和标准化的自适应机制给出，在2004年被提出用于实时估计未知信号，同时可以用于测量正弦信号。ANF的结构框图[13]如图1所示。

图1 ANF结构框图

1.1 ANF原理

ANF结构的数学描述为：

(1)

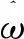
(2)

式(2)微分方程组的唯一解为：

(3)

1.2 ANF的频率特性

(4)

将s=jω1代入式(4)，得：

(5)

根据输入信号和输出信号的关系，结合ANF的传递函数，可以得到x的表达式为：

(6)

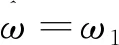
(7)

由式(7)可知：

(8)

(9)

此时根据式(6)可得x2的表达式为：

(10)

将微分方程组中式(1)的第一式带入第三式得：

(11)

(12)

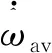
(13)

由式(13)计算出频率检测响应速度，用频率检测响应的时间常数τ表示：

(14)

通过式(14)可知，频率检测响应速度受输入信号频率ω1和幅值A1的影响，在频率ω1和幅值A1保持恒定前提下，ANF的动态响应速度只取决于阻尼比ξ和自适应增益γ。因此，参数ξ和γ需要根据实际需求衡量设定，从而使ANF得到最佳响应。

2 多结构ANF正负序分量提取

2.1 不平衡电压正负序分量提取

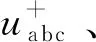
(15)

(16)

式中a是一个为ej2π/3的复数运算符。

然后，通过Clark变换将uabc的正负序电压分量转换到静止的αβ坐标系下。

(17)

同理，得：

(18)

式中q=e-j2π是一个移相算子，在αβ静止坐标系下产生90度相移的电压矢量信号。

2.2 多结构ANF

依据电网不平衡时电压正负序分量的提取方法，需要将三相电压变换到在αβ静止坐标系下，αβ静止坐标系下ANF的数学描述为：

(19)

根据1.1节中的分析方法，式(19)可以简化为：

(20)

频率响应速度的时间常数：

(21)

三相电压变换到αβ静止坐标系下，提取出正负序分量的同时，由频率响应的时间常数ταβ看出，由于将三相电压变换到αβ轴上，简化了三相ANF的结构和运算量，明显加快了三相系统中多结构ANF的频率响应速度，频率响应的时间常数大致为单相系统的3倍，三相系统的1.5倍。

在不平衡的电网信号中，正负序分量的提取需要αβ坐标系中下的估计信号uα、uβ及它们的正交分量，考虑到ANF结构可以产生一组正交分量，因此可以将uα、uβ及正交分量由ANF-α和ANF-β两个并行的ANF结构实现，结合瞬时对称分量理论，通过简单的数学运算计算出基波的正负序分量。结合以上分析，可以得到正负序分量提取的结构，多结构ANF正负序提取的结构框图及频率检测单元分别如图2、图3所示，其中频率检测单元是多结构ANF正负序提取结构框图的子结构，作为基波频率的动态响应部分，从而完成多结构ANF正负序分量提取的自适应过程

图2 基于多结构ANF正负序提取的结构图

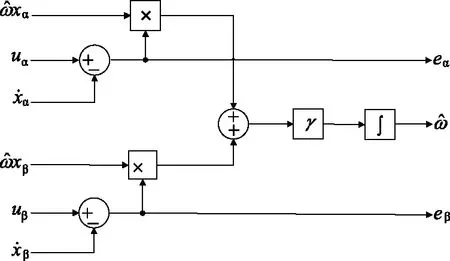
图3 多结构ANF的频率检测单元

正负序分量提取结构主要由频率检测单元、两个ANF结构和正负序计算模块组成。首先将三相电压变换到在αβ静止坐标系下，通过两个并联的ANF模块得到αβ静止坐标系下的两组正交分量，两组正交信号经过正负序计算模块进行数学运算，计算出基波的正负序分量。同时参考ANF结构的频率估算结构，将两组信号的估计误差参数eα和eβ进行叠加，通过自适应增益系数γ调节传递函数的带宽，从而实现频率值的准确追踪。

3 改进的多结构ANF

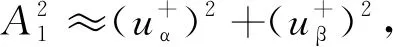
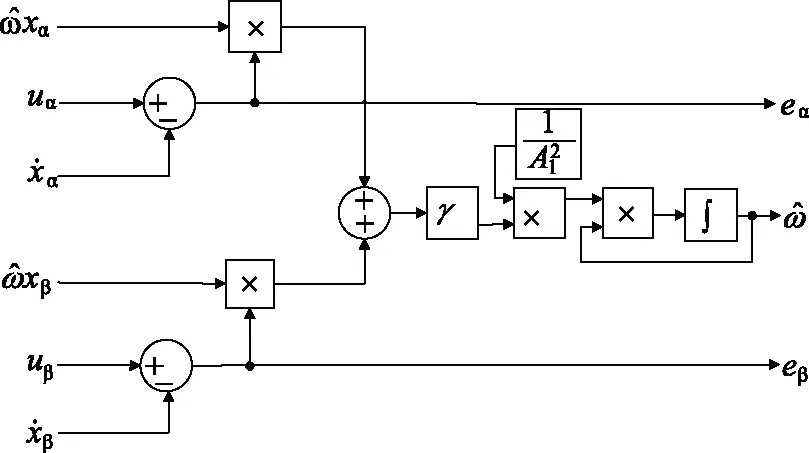
图4 改进的多结构ANF的频率检测单元

改进的多结构ANF的频率检测单元增加了两个乘法节点，将基波的幅值和频率引入频率更新方程，消除幅值和频率对频率响应时间常数的影响，实现频率响应时间常数与基波频率、幅值的解耦。当电网工况不稳定时，抑制了幅值变化和频率跳变的影响。因此，将改进的ANF结构应用到基波正负序分量提取时，动态响应具有幅值频率自适应性，同时基波正负序提取的追踪速度明显提升。

4 仿真分析

为验证改进后多结构ANF的理论分析正确性，在MATLAB/Simulink下搭建仿真模型，仿真模型如图5。

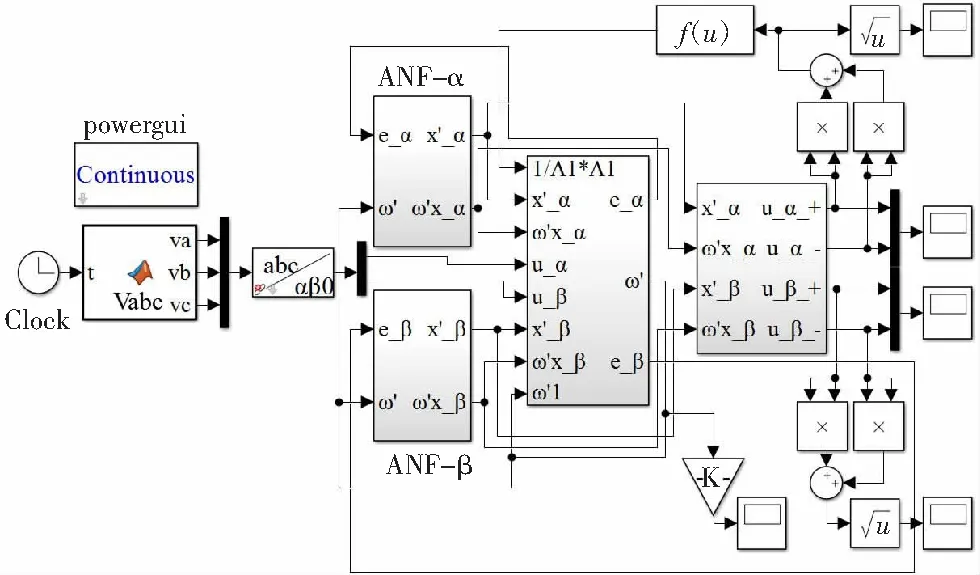
图5 改进的多结构ANF仿真模型

初始条件为：决定ANF追踪速度的参数γ=800，ξ=0.7。三相输入信号中，A相电压信号可以表示为：u(t)=A1sin(ω1t+φ1)，其中，输入信号幅值A1=10 V，角频率ω1=2πf=100π，初相位φ1=π/3。在t=0.3时，电网信号的频率由50Hz跳变为60Hz，同时三相电网电压出现不平衡现象，三相电压分别跌落40%、50%和60%；t=0.4时，三相电网重新回到平衡状态，频率重新变为50 Hz。图6为改进后多结构ANF基波正负序分量提取及幅值频率估计的仿真波形。

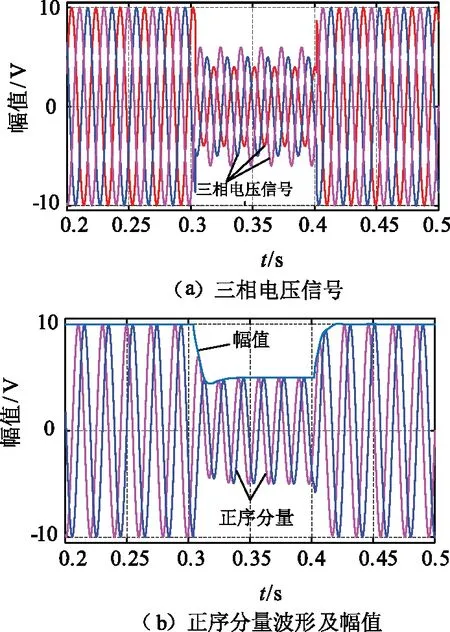
图6 改进的多结构ANF提取波形

从仿真结果可以看出，改进型多结构ANF可以准确的实现三相电网电压正负序分量的提取，同时能够实现对正负序分量的幅值和频率的准确估计。基波正负序分量经过1个基波周期左右能够准确提取，幅值在1.5个基波周期后可以实现准确追踪。当电网电压不平衡发生时，1.5个基波周期就能实现频率的估计。

为验证改进后多结构ANF的性能优势，结合理论分析的基础，仿真对比改进型多结构ANF正负序分量提取和多结构ANF正负序分量提取的波形，对比提取的正负序分量的幅值及频率响应。同时，为保证仿真条件的一致性，在t=0.3时，频率由50 Hz跳变为60 Hz，且三相电网电压分别跌落40%、50%和60%；在t=0.4时，频率重新变为50 Hz，三相电压回到平衡状态，其它初始值相同。仿真结果如图7所示。

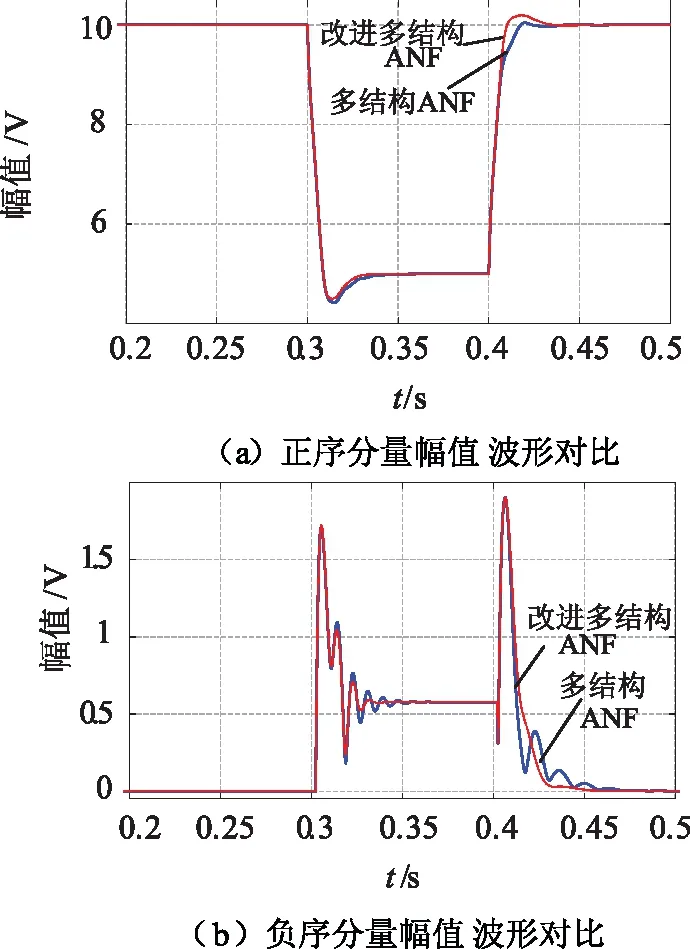
图7 多结构ANF与改进多结构ANF波形对比

由仿真结果可以看出，两者都能很好的追踪到基波正负序分量，同时估计出基波的频率。但电网电压出现不平衡现象时，改进型多结构ANF不需要1.5个基波周期就能估计出电网的频率，能够更快速的估计出电网频率，而且改进型多结构ANF追踪幅值的波动较小，加强了对幅值波动的自适应性。当三相电网频率波动和电压不平衡时，性能优势得到了大大的体现。

5 结束语

本文将原有ANF的频率检测单元改进，将检测的基波频率和幅值引入到原有ANF的频率检测单元中，使频率响应的时间与基波频率和幅值解耦，消除基波频率跳变和幅值变化的影响，使频率检测单元具有了频率与幅值的自适应性。在分析多结构ANF基波正负序分量提取的正确性基础上，将改进后的ANF结构应用于基波正负序提取中。仿真结果表明，改进后的多结构ANF在保留原有多结构ANF优势的同时，在三相电网电压的不平衡时，有更好的性能和抗畸变能力，能够减少幅值变化和频率跳变对正负序分量提取的影响。