基于小波阈值去噪的直流充电桩电能计量数据去噪算法研究

章江铭，沈建良，袁键，潘权锋，颜加松，李静

(1.国网浙江省电力有限公司营销服务中心，杭州 310000； 2.杭州意能电力技术有限公司，杭州 310000；3.哈尔滨电工仪表研究所有限公司，哈尔滨 150028)

0 引 言

随着国家推动绿色转型实现积极发展，壮大节能环保、清洁能源，推动低碳绿色交通、车辆电动化等战略实施[1]。到2020年，纯电动汽车和混合动力汽车生产能力达到200万辆，截至2019年年底，我国新能源汽车保有量已达到381万辆[2]，全国充电基础设施规模达到120万个[3]，新能源汽车因为其良好的环保性能以及节约能源的特点，能够有效减弱对环境的危害，已成为汽车行业发展的趋势[4]。但与此同时，与之配套的充电设施建设却成为了制约新能源汽车快速发展的主要短板之一。目前，随着直流充电站的建设，直流快充由于其快速高效的特点正逐渐取代交流充电，成为充电站主流充电方式[5]。作为实施强制管理的计量器具，充电桩准确的电能计量课确保电能交易公平公正[6]。但目前直流计量方法还不够成熟，且电动汽车接入电网进行充电后，由于其充电设备自身具有的非线性特性，将会引起充电桩输出侧产生纹波[7]。电动汽车直流快充的充电电流和电压的幅值及变化范围都会比交流慢充更大，不能直接借鉴交流计量方法[8]。现阶段，国内外众多学者从不同方面对直流电能计量准确度影响因素展开了深入的研究，尤其纹波产生的计量误差已引起诸多关注。文献[9]对高频电源的纹波系数作了较详细的讨论。文献[10]通过研究电能计量装置在直流电能纹波、电源突变、暂降、中断等情况下的工作特性，分析了不同幅度和不同频率纹波对直流计量的影响。文献[11]研究和分析了直流电能计量不同算法对带有纹波的高功率直流计量时存在的误差影响。并分析了纹波影响规律，在此基础上定量确定高功率状态下直流纹波对直流计量影响。上述文献对于纹波造成的计量准确度影响进行了分析。文献[12]从直流电能表专用心片和计量算法两方面分析了纹波对直流电能计量的影响，并提出直流电能计量中对高、低频纹波抑制的硬件措施。文献[13]提出一种抑制直流大电流源纹波的新型方法，采用双铁芯磁平衡式电流传感器，使得电感铁心直流磁通近似为零，与传统抑制纹波方法相比，具有低损耗、低成本、高效率和易控制等特点。文献[14]通过研究整流性负载、开关充电设备以及快速动态变化负荷的直流电能产生原理，结合电能表计量算法和实验阐述了计量过程中存在的误差影响，提出了不同计量场合下减少计量误差的算法参数优化方法。论文将辅助上述文献提出的纹波抑制措施，在算法方面提高计量准确度。文献[8]采用离散小波消噪法对对采样电压和采样电流信号进行滤波处理，进而得到功率。但由于软阈值处理之后的小波系数与小波系数总存在固定的偏差，上述文献采用的小波软阈值去噪法会造成去噪后的信号与电压、电流基波信号之间存在偏差[15]。故本文采用改进小波阈值函数法对信号进行抑制纹波处理，解决传统小波函数存在的信号震荡、产生恒定偏差等问题，将其应用到直流滤波当中，得到更加接近原始直流信号的滤波信号，并与其它滤波方法进行效果对比，分析本滤波方法的优异之处，从算法方面来提高直流计量数据的准确度，这对直流充电计费以及检定具有重大的意义。

1 直流电能表电能计量理论分析

1.1 直流电能计量

直流电能的测量采用电压、电流有效值相乘得出直流功率后再计算电能值[16]，或使用瞬时功率积分计算电能值[17]。充电桩内置直流计量模块使用的是电子式智能电能表，计量准确度主要取决于乘法器。实际测量电能时，由于直流信号夹杂着包含着纹波以及各种脉动的噪声信号，并不能达到理想的计量结果，所以将分析纹波含量对电能计量算法的影响。目前主要的直流电能计量算法有三种[11]：

(1)电压、电流平均值法。

W1=P1·Δ=U0I0·Δ

(1)

式中U0、I0分别为Δ时间内平均直流电压和电流。

(2)电压、电流有效值法。

W2=P2Δt=UIΔt

(2)

式中U、I分别为Δ时间内平均直流电压和电流。

(3)瞬时功率积分计算直流电能。

(3)

式中T表示单位周期；u(t)、i(t)分别为T时间内随时间变化的电压函数与电流函数；u0(t)、i0(t)分别为电压直流分量函数与电流直流分量函数；uk(t)、ik(t)分别为k次谐波电压分量函数与k次谐波电流分量函数；U0为电压直流分量;I0为电流直流分量;Uk为k次谐波电压有效值;Ik为k次谐波电流有效值;αk为k次电压谐波分量初始相位;βk为k次电流谐波分量初始相位。

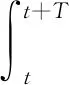
(4)

式中W3表示在单位周期T内瞬时电压和电流的积分电能。

但在实际电能计量中，对瞬时功率的采集并不是严格连续的，通常需要设定采样间隔Δ，在单位周期T内，采集次数为N，当Δ的数值足够小，采集次数足够多，瞬时功率积分法的电能计算表达式可化为：

(5)

在理想状态下，三种计算方案的结果都是准确一致的，但现实环境下的直流信号往往携带纹波信号，需要进行纹波环境下的电能计量误差运算分析。

1.2 充电桩输出纹波分析

直流纹波系数反应了直流信号中的纹波含量，在电动汽车非车载充电机电能计量标准中，直流纹波系数可表征为纹波有效值系数和纹波峰值系数[18]。纹波有效值系数定义为输出交流分量有效值与该直流输出电压平均值之比，纹波峰值系数定义为输出交流分量峰峰值与该直流输出电压平均值之比。其运算如式(6)、式(7)所示：

(6)

(7)

式中UDC为直流输出电压平均值;Ums、Xms分别为输出交流分量有效值和纹波有效值系数;UPP、XPP分别为直流输出交流分量的峰峰值和纹波峰值系数。根据国标，电源输出纹波有效值系数Xms不应超过1%，纹波峰值系数XPP不应超过0.5%。

电压、电流平均值计算直流功率P1和“有功”功率P3的相对误差为:

(8)

(9)

故当0≤a、b≤0.5%，0<θ≤360°时，通过MATLAB对于直流输出平均值功率P1仿真，ε31分布如图1所示。

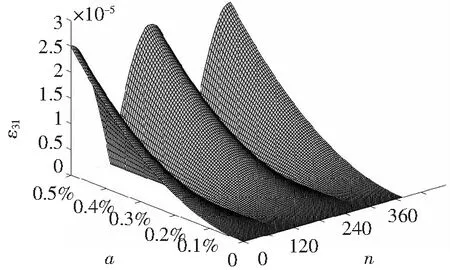
图1 平均值法计算直流电能误差ε31分布图

电压、电流平均值计算直流功率P2和“有功”功率P3的相对误差为：

(10)

当0≤a、b≤0.5%，0<θ≤360°时，通过MATLAB仿真，ε32分布如图2所示。

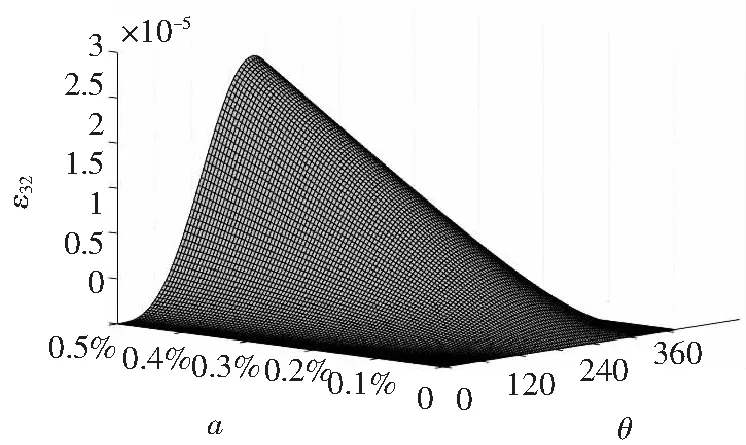
图2 有效值法计算直流电能误差ε32分布图

通过仿真可以看到，计量法所产生的误差都与直流电量中纹波分量a成正相关，并且a所占百分比越大，误差越大。接下来对直流充电计量数据滤波算法进行优化，提高计量准确度。

2 电能计量用数据处理算法

因为充电机输出的直流信号中会含有各种噪声，为了滤掉信号的干扰，采用数字滤波器进行采样数据处理。

2.1 经典滤波算法

平均值法适用于滤除随机干扰，加权平均值法速度慢计算量大[19]。如图3所示，采用中值滤波法、限幅滤波法、滑动平均值法对直流信号进行滤波处理。

从仿真图3中可以看出，中值滤波对于处理偶发性波动或采样器不稳定而造成的误差所引起的脉冲干扰比较有效，但对快速变化的直流电压信号处理效果不佳。

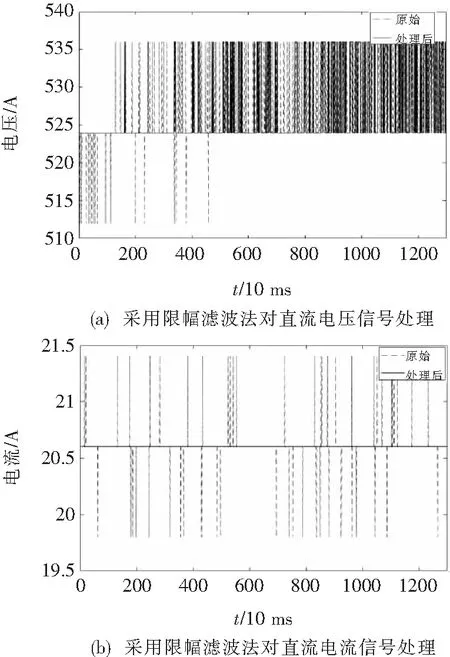
图3 采用中位值滤波法对直流信号处理

从图4仿真结果中可以看出，限幅滤波法对偶发性干扰抑制效果好，对周期性的干扰抑制效果差。

图4 采用限幅滤波法对直流信号处理

从滑动平均值滤波法的图5仿真结果中可以看出，对周期性干扰滑动平均值法抑制效果较好，对偶发性干扰抑制效果较差。

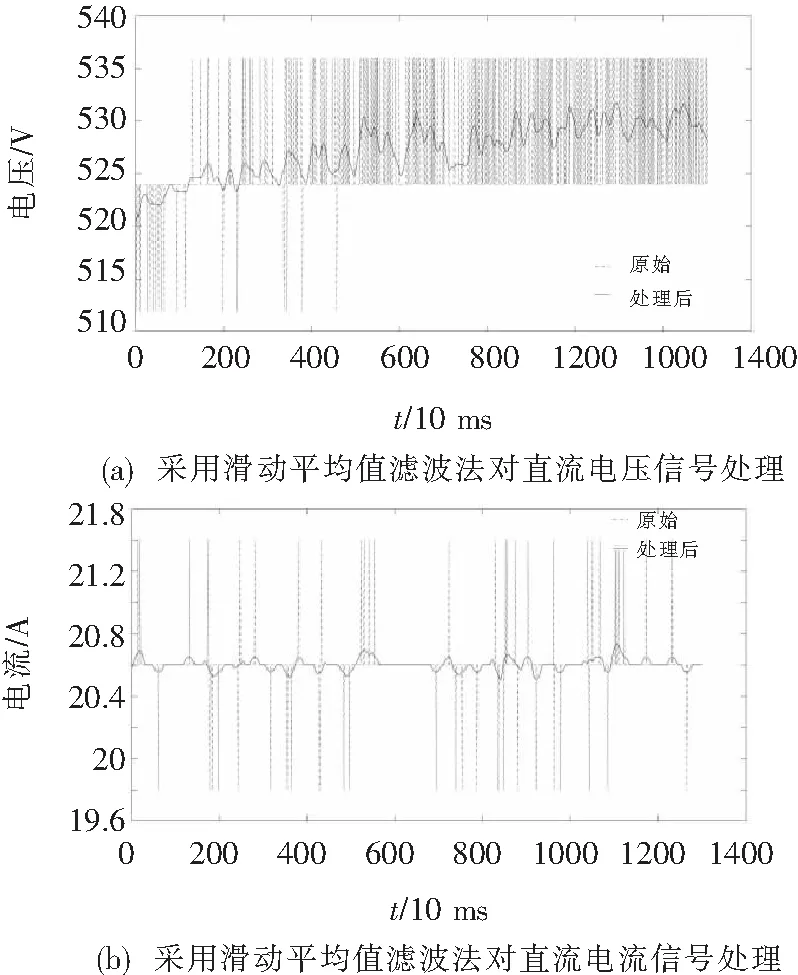
图5 采用滑动平均值滤波法对直流信号处理

综上，直流充电桩输出的直流电压原始信号中含有较多的脉动量，纹波波形淹没在这些脉动量中，在图中无法观测。对比三幅子图，可看出采用滑动平均值滤波法处理后的信号波形更为平滑，抖动幅度相对较小，比前两种方法的滤波效果要好。直流充电桩输出直流电流原始信号脉动量比电压信号少，脉动量基本是一个采样点对应的波形。对比三幅子图，可看出采用中位值滤波法处理后的信号失真较为严重，采用限幅滤波法处理后的信号波形抖动较大，滤波效果不佳。采用滑动平均值滤波法处理后的信号波形比较平滑，抖动相对较少，滤波效果更佳。但滤除了过多的直流脉动量，会对电能计量产生误差，去噪后信号比较简单。

所以对比经典去噪算法，文中引入了现代滤波法中的小波阈值去噪法对直流信号进行滤波处理。小波变换有可在整个频率范围内进行滤波的特点[8]，已成为用于电能质量信号检测与分析最多的去噪方法[20-21]。

2.2 小波阈值去噪

小波阈值函数是能否对直流信号准确进行去噪的关键，选择一个合适的阈值可以提高去噪质量，提高计量的精确度。阈值过大，可能导致信号过于平滑，滤掉信号的细节分量；阈值过小，滤波效果较差，仍存在较多的噪声。所以本文分别采用不同的阈值进行滤波处理，并通过MATLAB进行仿真，对比仿真结果，观察滤波处理前后信号的变化。

直流充电桩电能计量数据小波阈值去噪法的数据处理步骤如下：

(1)首先选择合适的小波基和分解层数对含噪的直流信号进行小波变换，得到各分解层对应的小波系数；

(2)再选取门限阈值和阈值函数，计算出阈值，对各层小波系数进行量化；

(3)最后对量化后的小波系数进行重构，从而得到输出的去噪直流信号。

传统的阈值去噪的方法分为硬阈值去噪法、软阈值去噪法。硬阈值函数的表达式为：

(11)

式中y为处理后的输出函数;ωj,k为分解后的小波系数；Tj为设定阈值。

软阈值函数的表达式为：

(12)

软阈值去噪法虽然连续性好，但是会损失很多有用的信号能量，重构后出现误差，信噪比较低。

传统的小波阈值选取规则主要包括以下四种：

(a)无偏风险估计准则(rigrsure)：即一种基于Stein的无偏似然估计原理的自适应阈值选择方法。具体方法如下：

(1)把信号种得每一个元素取绝对值，再由小到大排序，然后将各个元素取平方，从而得到新的信号序列。

(2)若取阈值为新序列的第k个元素的平方根，即

(13)

式中λk为平方根，f(k)为得到的新序列，k=0,1,……，n-1

则阈值产生的风险为：

(14)

(3)根据所得到的风险曲线Rish(k)，得其最小风险点所对应的值为kmin，则rigrsure阈值定义为：

(15)

(b)固定阈值准则(sqtwolog)：表达式为：

(16)

式中n为信号长度。

(c)混合准则(heursure)，它是rigrsure和sqtwolog准则的混合，信噪比较大时，heursure 自适应选择rigrsure，相反情况下自动调整为sqtwolog模式。

(d)极小极大准则(minimaxi)：也是一种固定阈值选择形式。表达式为：

(17)

相比于固定阈值，自适应阈值可在小波分解层的每个方向寻找一个阈值最匹配的阈值来进行去噪，故本文采用rigrsure准则与heursure准则选取阈值进行小波阈值滤波处理。

图6为直流充电桩充电实测数据，现对图6进行小波阈值去噪，取用小波基 ，分解层数 ，处理效果如图6所示。

图6 直流充电桩充电实测数据

图7为rigrsure规则计算的软阈值小波去噪算法数值仿真结果，电压、电流的数据误差要远远小于经典滤波法，能直观的看出数据在经过处理后更加的平稳和准确，滤波效果较好，有助于提高下一步电能计量的精度。

图8为采用heursure规则确定的软阈值小波去噪算法数值仿真结果，通过图6、图7的仿真曲线可看出，相比与rigrsure规则计算的软阈值，采用heursure规则确定的软阈值对原始直流信号滤波效果更好，幅值范围减小且不存在硬阈值间断点导致的信号振荡问题，但软阈值去噪后的信号与纯净信号之间的恒定偏差又会引入新的误差，影响直流输出计量的准确性。

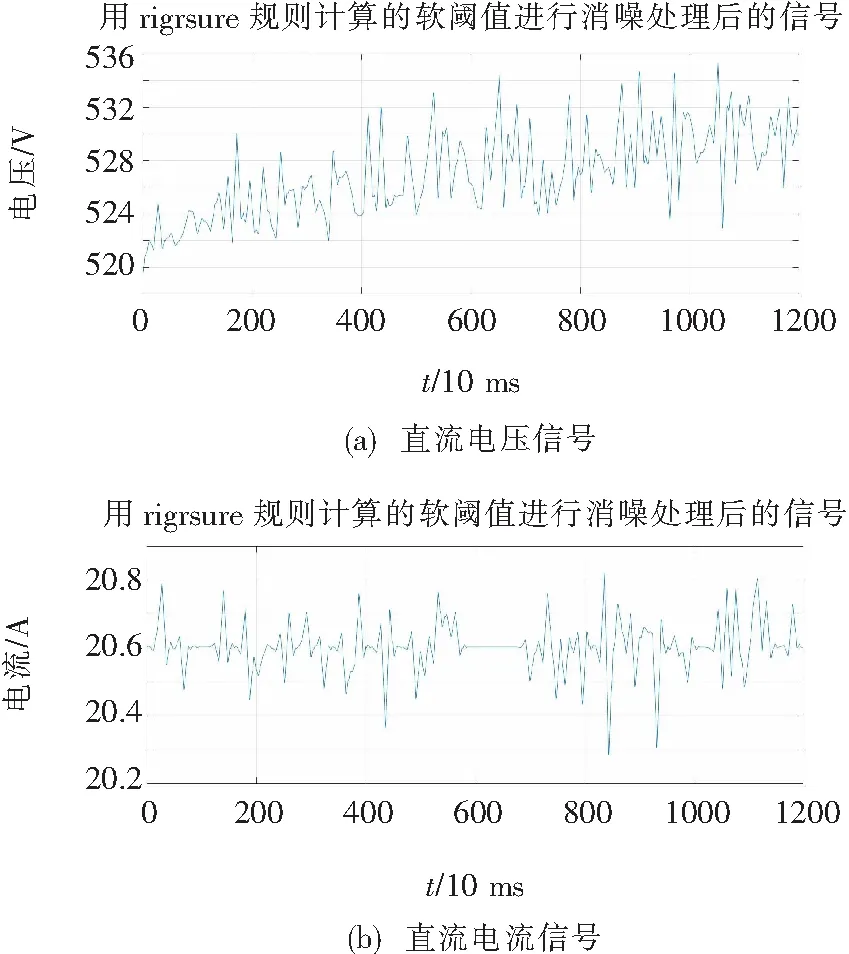
图7 采用rigrsure软阈值滤波法对直流

图8 采用heursure软阈值滤波法对直流

3 改进小波阈值去噪

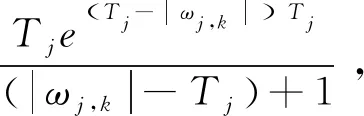
(18)

式中y为硬阈值处理之后的小波系数;ωj,k是第j尺度上的第k个小波系数，

证明阈值函数的连续性：

(19)

(20)

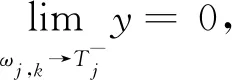
证明阈值函数的偏差性：

当ωj,k→∞时，

(21)

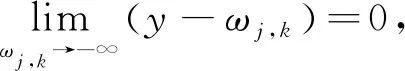
改进阈值函数的渐近性：

当ωj,k→∞时，

(22)

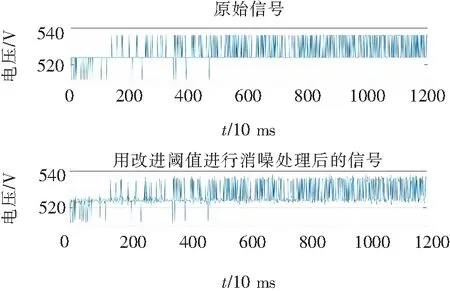
图9 采用改进阈值函数对直流电压信号处理

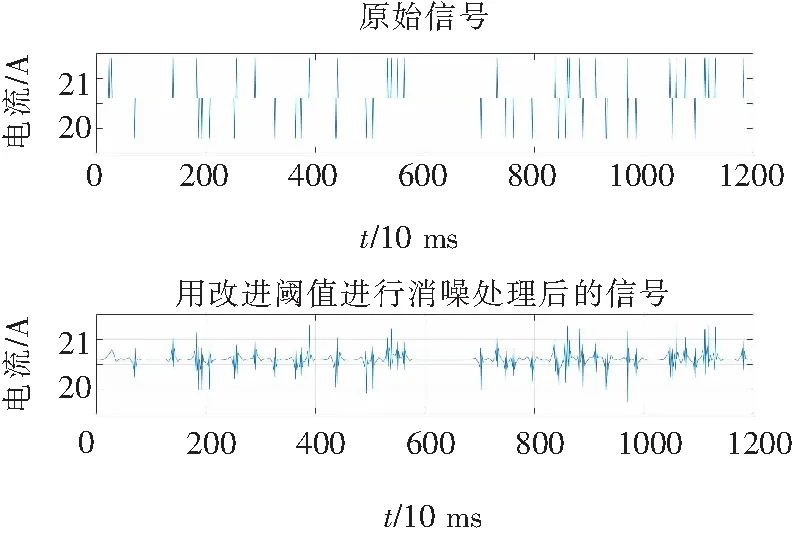
图10 采用改进阈值函数对直流电流信号处理

通过对比仿真波形图8～图10可以看出，相比于传统阈值函数的小波去噪方法，经本文改进的小波去噪方法处理后的直流电压、电流信号的滤波效果更好，波形相对更为平稳，幅值变化范围更小，数据更准确，且不存在信号震荡与恒定偏差问题，得证所提方法能够更加有效的滤除直流充电桩输出信号中的纹波，保留原信号的充电特性，提高直流电能计量精度。接下来再通过信噪比(SNR)与均方根误差(RMSE)来衡量各阈值去噪方式的降噪效果，如表1所示。

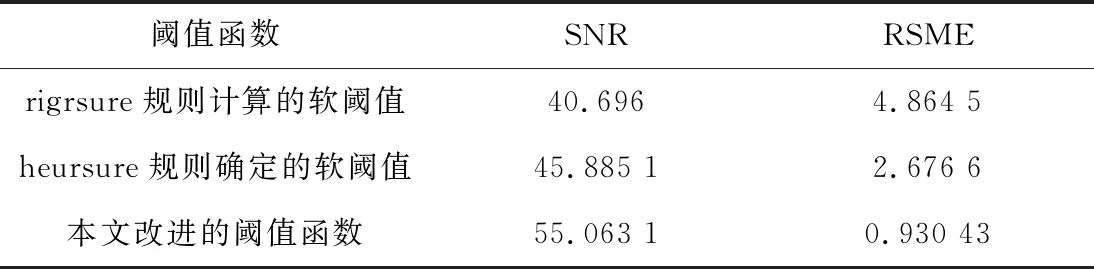
表1 不同去噪方式的SNR与RMSE对比

从表1中可以看出，对比三种去噪方式的SNR，文章提出的改进阈值函数明显要高于rigrsure规则计算的软阈值与heursure规则确定的软阈值，高出10～15左右。同时，对比三种去噪方式的RSME，本文提出的改进阈值函数要明显远低于其它两种，表明去噪后的信号在提高信噪比的同时更加稳定，能更好地反映电能信号的真实情况。故在实测直流充电桩数据的去噪处理中，本文改进的小波阈值函数去噪法信噪比较大，均方根误差较小，降噪效果优于其他两种算法。

综上所述，通过分析仿真结果以及表1的对比分析，文中采用的改进阈值去噪法对直流充电桩输出直流电信号中的纹波滤除效果最好，在最大程度上接近原始信号的电能的计量。

4 结束语

文章在分析直流计量算法的基础上，针对直流充电桩为电动汽车充电过程中产生的纹波影响电能计量准确性的问题，引入了改进小波阈值消噪算法，用此方法对充电电压、电流数据进行滤波处理，并对提出的滤波算法进行了数值仿真，验证了运用改进小波阈值消噪算法能在保留原信号的充电特性的同时，有效滤除直流充电桩输出信号中的纹波，能够大幅度提高直流充电桩电能计量的准确性。