基于改进多目标灰狼算法的冷热电联供型微电网运行优化
2022-06-08戚艳尚学军聂靖宇霍现旭邬斌扬苏万华
戚艳,尚学军,聂靖宇,霍现旭,邬斌扬,苏万华
(1.国网天津市电力公司电力科学研究院,天津 300384; 2.天津大学 内燃机国家重点实验室,天津 300072)
0 引 言
随着分布式能源供应系统的快速发展,热电联供(CHP)系统以及冷热电联供(CCHP)系统已成为提高能源效率和减少温室气体排放的关键解决方案[1]。CCHP系统采用能量梯级利用原理,使系统的能源利用效率显著高于普通热电效率,实现节能减排的目标。深入对CCHP型微电网的研究,致力于多种能源系统的协调运行,提高微电网运行的经济性和环保性,对于CCHP型微电网的推广与发展有着重要意义[2-3]。
目前,微电网的经济调度研究主要考虑经济和环保两方面的因素。文献[4]中采用模糊几何加权的方法,建立了综合运行费用和环境惩罚因子的目标函数,对CCHP型微电网进行优化调度。这种将多目标问题转化为单目标的方法在微电网的运行优化研究中使用普遍[5],但是也存在一定的问题。单目标优化得到的运行策略单一,用户无法进行灵活的选择。同时,单目标优化的结果无法使用户直接对运行策略的经济性和环保性进行调控,单纯以最佳的经济效益为目标。文献[6]中采用MOPSO对热电联供型微电网进行基于Pareto最优解集的多目标运行优化。优化结果中,用户可以直观地得到污染气体排放和运行费用的具体情况。基于Pareto最优解集的优化结果具有多样性,用户在各种优化策略中可以结合实际需要,权衡污染气体排放和运行费用,做出最优选择。
如今,多目标优化技术广泛应用于:机械工程、土木工程和化工等研究领域。早期的多目标随机优化算法多为单目标优化算法转化而来,例如:SPEA[7]、NSGA-Ⅱ[8]、MOPSO[9]和MOEA/D[10]等应用广泛的优化算法。文献[11]提出了一种基于灰狼优化算法(GWO)提出的多目标灰狼优化算法(MOGWO),该算法具有收敛快、实现简单的特点,并且在多目标基准测试函数中表现出优于MOPSO和MOEA/D的性能,具有应用推广的潜力。然而,相同的优化算法在不同的实际问题中的优化性能无法得到保证,其在微电网多目标优化问题的适用性尚待验证。
文中以CCHP型微电网为研究对象,将微电网的运行费用和环境污染成本作为优化目标,考虑冷热电负荷和设备运行要求的约束,建立的微电网的多目标优化模型,使用改进的MOGWO算法进行求解。最后,通过仿真结果验证模型和改进算法的适用性与有效性。优化结果具有多样性与灵活性,以供用户根据需要进行选择,实现CCHP型微电网经济环保的运行。
1 CCHP型微电网数学模型
文中研究的CCHP型微电网,由风机、光伏电池、微型燃气轮机、蓄电池和大电网承担电负荷,此系统与大电网根据需求进行买/卖电;余热锅炉、蓄热槽和电采暖承担热负荷;溴化锂吸收式制冷机和分体式空调承担冷负荷,如图1所示。下面对主要微源的模型进行详细介绍。
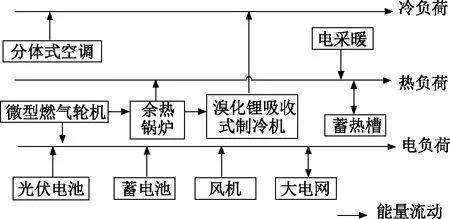
图1 CCHP型微电网
1.1 微型燃气轮机模型[6,12]
微型燃气轮机的效率与设备容量、负载水平相关。其效率的表达式为:
ηMTE=4.08×10-4PMTref+0.107RMT-8.91×10-5PMTrefRMT+0.169
(1)
ηMTH=-6.64×10-4PMTref-6.87×10-2RMT-1.33×10-4PMTrefRMT+0.693
(2)
式中hMTE为发电效率;hMTH为制热效率;PMTref为设备的额定功率;RMT为荷载率。
1.2 余热锅炉模型
微型燃气轮机的烟气作为余热锅炉的热源,产生蒸汽满足微电网的热负荷需求,额外的蒸汽还可以通过吸收式制冷机供冷。余热锅炉的功率为:
(3)
式中Pbl为余热锅炉的功率;PMT为微型燃气轮机的功率;hbl为余热锅炉的效率。
1.3 溴化锂吸收式制冷机模型
溴化锂吸收式制冷机利用余热锅炉产生的蒸汽进行吸收式制冷,其数学模型为:
Pac=Qac·COPac
(4)
式中Pac为溴化锂吸收式制冷机的制冷功率;Qac为余热锅炉为提供个制冷机的热量;COPac为设备的制冷系数。
1.4 蓄电池模型
蓄电池可以储存微电网中产生的多余电量和在用电高峰时段进行辅助供电。蓄电池的充放电状态(SOC)为剩余电量与额定电量的比值:
(5)
式中Cnet蓄电池当前电量;C为蓄电池最大容量。
每个时间段蓄电池状态:
(6)
式中Pb为电池功率,放电为正;Δt为时间跨度。
1.5 蓄热槽模型
蓄热槽可以储存微网产生的剩余热量并加以利用,但在储热过程中会造成热能的耗散。蓄热槽的具体模型为:
EHST,t+Δt=EHST,t(1-φHST)Δt+ΔtPHST,t
(7)
式中EHST,t为t时段蓄热槽内的热能;jHST为蓄热的损耗系数;PHST,t为设备t时段的功率,蓄热为正,放热为负。
1.6 风力机模型
风力机的输出功率表达式为:
(8)
式中Pw为风力机输出功率;Vin切入风速;Vout切出风速;v当前风速;Vr为额定风速;PN风力发电机组额定输出功率。
1.7 光伏电池模型
光伏电池的输出功率表达式为:
(9)
式中Ppv为光伏电池的输出功率;PSTC标准条件下的输出功率;G为实际光照强度;GSTC标准条件下的光照强度,1 000 W/m2;k为功率温度系数;Te为环境温度;TN为组件额定温度;TSTC模块在标准条件下的表面温度,25 ℃。
1.8 电采暖和分体式空调模型
当其它微源无法满足冷热负荷时,需要消耗电能来满足用户的需求。分体式空调的制冷功率表达式为:
Pec=Qec·COPec
(10)
式中Pec为分体式空调的制冷功率;Qec为消耗的电功率;COPec为分体式空调的制冷系数。
电采暖的制热功率表达式为:
Peh=Qeh·COPeh
(11)
式中Peh为电采暖的制热功率;Qeh为消耗的电功率;COPec为电采暖的制热系数。
2 微电网多目标优化模型
2.1 目标函数
微电网的优化目标包括2个:最低的微电网运行费用、最低的环境污染成本。
2.1.1 微电网运行费用模型
微电网运行费用包括三个方面:天然气费用、各微源的维护费用和微电网从大电网购售电产生的费用。优化目标的数学表达式为:
(12)
式中F1为系统运行24小时总费用;N为微源的数量;Cgas为天然气价格;Pj为微源j的功率;Cj为微源j的维护单位成本;l为弃风成本系数;Pw,e为弃风功率;t为弃光成本系数;Ppv,e为弃光功率;Cp为从大电网购电价格;Cs为向大电网售电价格;Pg为微电网与大电网的交互功率,购电为正售电为负。
2.1.2 环境污染成本模型
微电网中产生污染气的微源主要为微型燃气轮机和大电网,单纯的将污染气体的排放总量相加无法反映其对环境的影响程度,文中将微网产生的污染气体的治理成本最少作为目标进行优化,具体的数学表达式为:
(13)
式中F2为系统运行24小时产生污染气体总的治理费用;k表示污染气体的种类(包括CO2,NOx和SO2);WMT,k表示微型燃气轮机产生污染气体k的排放系数;Wg,k表示大电网产生污染气体k的排放系数;Pg,p表示从大电网的购电功率(售电时为0);Ck表示污染气体k的单位治理成本。
2.2 约束条件
微电网优化模型的约束条件主要包含两个方面:负荷约束和微源的运行约束。
2.2.1 电负荷约束
微电网各个微元输出的电功率之和需满足电负荷的需求。
蓄电池处于放电状态时:
(Pw+PMT+Ppv+Pbηdis+Pg=PE)i
(14)
蓄电池充电状态时:
(15)
式中PE为园区电负荷;hdis为蓄电池放电效率;hch为蓄电池充电效率。
2.2.2 热负荷约束
余热锅炉、蓄热槽和电采暖的输出热功率之和需满足园区热负荷的需求,且余热锅炉产生的蒸汽优先满足热负荷,多余的蒸汽可用于制冷和蓄热。但是由于蓄热槽的容量限制可能会造成热能的浪费。蓄热槽放热:
(Pbl+PHSTμdis+Peh≥PH)i
(16)
蓄热槽蓄热:
(17)
式中PH为园区热负荷;mdis为蓄热槽放热效率;mch为蓄热槽蓄热效率。
2.2.3 冷负荷约束
溴化锂吸收式制冷机和分体空调输出的冷功率之和需满足园区冷负荷需求:
(Pac+Pec=PC)i
(18)
式中PC为园区冷负荷。
2.2.4 储能设备的约束条件
为了保护蓄电池的工作寿命,蓄电池的SOC应处于一定的范围内:
(SOCmin≤SOC≤SOCmax)i
(19)
式中SOCmin和SOCmax是蓄电池电荷状态允许的最小和最大值。
蓄热槽的需热量也存在着一定约束:
(EHST,min≤EHST≤EHST,max)i
(20)
式中EHST,min和EHST,max是蓄热槽的蓄热量所允许的最小和最大值。
2.2.5 设备的运行约束
微电网内微源的运行功率都应该处于对应的范围内:
(Pj,min≤Pj≤Pj,max)i
(21)
式中Pj,min为微源j的运行功率下限;Pj为微源j实际运行功率;Pj,max为微源运行功率上限。
2.2.6 微型燃气轮机的爬坡约束
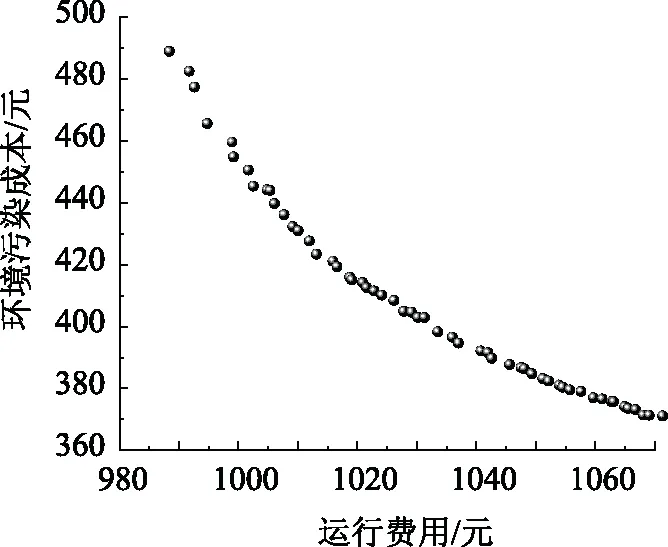
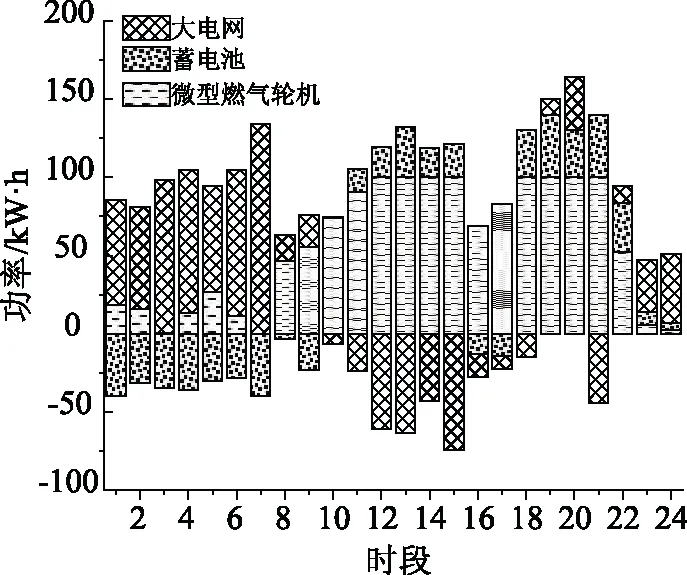
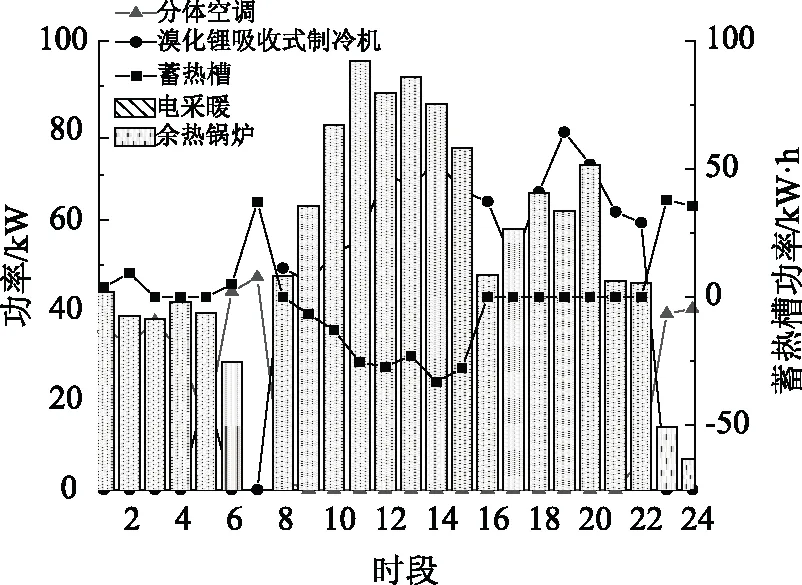
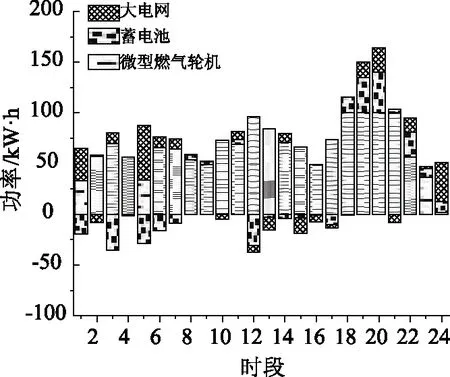
-Rdown (22) 式中PMT(t)、PMT(t-1)表示t、t-1时刻微型燃气轮机的功率;Rdown、Rup表示最大向下和最大向上爬坡速率。 2.2.7 与大电网交互功率的约束 为了减小微电网对大电网造成过大的负荷波动,影响大电网的稳定性,对微电网与大电网的交互功率进行一定的限制。 Pg,min≤Pg≤Pg,max (23) 式中Pg,min为与大电网交互的功率下限;Pg,max为与大电网交互的功率上限。 灰狼优化算法是文献[13]受狼群合作捕食过程启发而提出的新型群体智能优化算法。2015年又在此基础上提出了多目标灰狼优化算法(MOGWO)。 Di(k)=|C·Xp(k)-Xi(k)| (24) Xi(k+1)=Xp(k)-A·Di(k) (25) 式中Xp(k)表示猎物目前所在位置;C和A为影响系数,其计算公式如下: A=2aR1-a (26) C=2R2 (27) 式中R1和R2为[0,1]之间的随机数,a按照式(28)线性减小: (28) 在灰狼优化算法中,将每次迭代中目标函数值最优的三个位置依次分配给a、b和d,其余个体根据这三个最优个体位置更新自己的位置。相较于GWO,MOGWO中引入了外部种群Archive并对a、b和d的选择策略进行了改动。Archive用于储存每一代产生的优秀个体,即非支配解。并且按照一定的策略进行更新和删除。MOGWO算法直接从Archive采用轮盘赌的方式选择三只优秀个体作为a、b和d。最终,外部种群Archive中的个体即为优化问题的一组Pareto最优解。 文中微电网的优化问题是非线性的多约束问题,在利用原始MOGWO算法进行求解的过程中,众多约束条件使得算法的计算时间增加,为了改善这一问题本文对MOGWO算法及优化模型进行了如下改进: (1)优化模型的简化。通过对微电网优化模型的简化可以有效减少灰狼的维数从而缩短求解时间:风机和光伏电池的维护成本相对较低且没有燃料费用和污染排放,故在优化时可以按照可能的最大功率出力; (2)灰狼初始化和位置更新的方式改变。在原始MOGWO中灰狼个体位置的每一维坐标是同时生成的,即每个微源在24个小时内的出力同时生成。原算法灰狼的位置向量表示为: X=(xa,1,...,xa,24,xb,1,...,xb,24,xc,1,...,xc,24) (29) 式中a,b,c代表不同的微源,数字代表不同的时段。如某个设备在某个时段的功率不符合约束的要求,整个灰狼的位置都要进行重新生成,造成运算量增加。针对微电网的约束和时间段的相关性,本文将每只灰狼个体位置按时间分为24组,将同一时间段的设备出力分为一组进行初始化和更新,即: Xi=(xa,i,xb,i,xc,i) (30) 判定满足约束时再进行下一组设备出力的初始化或更新,24个组都满足约束后进行合并和后续运算。这种做法的优势在于,当某个时段的设备出力不符合约束时,只需重新生成该时段的设备出力而非个体的所有时段的设备出力,从而缩短计算时间。 (3)MOGWO算法的前期探索能力不足,对于式(28)中的控制参数a而言,a越大则算法的探索能力越强[14-15]。在文中将线性缩小的a改为式(31)的幂函数形式,以提高算法前期的探索能力,经多次求解发现当指数为4时优化效果最佳。 (31) 改进后的MOGWO算法的主要步骤如下: (1)步骤1:设置灰狼的数量、最大迭代次数、搜索范围和外部种群Archive的参数等控制参数; (2)步骤2:灰狼初始化。随即生成灰狼个体,检验是否满足约束条件,直至生成足够数量的合格个体。计算灰狼的目标函数值,确定非支配个体,更新Archive; (3)步骤3:从Archive中按轮盘赌法选择a、b和d狼,其余灰狼根据a、b和d狼的位置进行更新,检验新生成的灰狼是否满足约束条件,直至生成足够数量的合格灰狼个体; (4)步骤4: 计算灰狼的目标函数值,确定非支配个体,更新Archive; (5)步骤5:重复步骤3、步骤4,直至达到最大迭代次数; (6)步骤6:输出Archive中的灰狼位置,即为微电网优化问题的一组Pareto解集。 微电网优化所需数据包括:冷、热、电三种负荷的预测(图2)、微源的相关参数和维护费用(表1)、与电网交易的电价(表2)、污染气体排放系数(表3)和天然气价格等。园区所用蓄电池的容量下限和上限为160 kW·h和480 kW·h,初始电量为160kW·h。蓄热槽的容量EHST,min和EHST,max为0和200 kW·h,初始蓄热量为100 kW·h。微型燃气轮机的燃料为天然气,价格为:Cgas=0.175元/kW·h。 图2 冷、热、电负荷预测 表1 微源的相关数据 表2 与大电网交易价格 表3 污染物排放系数及治理成本 4.2.1 模型仿真 前文已在微电网的优化模型的基础上对MOGWO进行了改进,风机和光伏电池按照预测的最大功率的出力(图3),当风机和光伏的出力溢出,产生的弃风、弃光也已考虑在运行费用中。模型中其它需要直接进行输出功率优化的微源包括:微型燃气轮机、蓄电池和大电网,其余微源的出力可以根据数学模型和约束条件得到。灰狼位置的每一维坐标代表某个微源一个时间段内的出力,维度为72。 图3 风机和光伏电池的出力预测 优化模型中,搜索灰狼个体的数目为100,最大迭代次数为200,外部种群Archive的容量为70。仿真结果得到70个Pareto最优解,即种可供用户选择的控制策略,每个控制策略的运行费用和环境污染成本各不相同,具体的解集如图4所示。 图4 优化结果 4.2.2 优化运行策略的分析 图5中是运行费用最小时的电功率出力优化。图中的电功率曲线没有包含风机和光伏电池的出力,风机和光伏电池的出力按照前文的预测值计算,剩余的电负荷由微型燃气轮机、蓄电池和大电网承担。从图5中可以看出,燃气轮机满负荷工作的时间段为第12~15和18~21时段,因为电费的峰时包含在这两个时间段内,此时燃气轮机的发电成本低于从大电网购电的费用,另外满负荷工作的燃气轮机有更高的效率,为了降低运行费用优先使用燃气轮机供电。另外,燃气轮机在电价处于谷时的第1~6和23~24时段出力很低,微电网优先使用更加廉价的大电网供电,可以进一步降低成本。 图5 运行费用最低策略的电功率出力 蓄电池的功率和蓄电量如图6所示。在第1~9和16~17时段蓄电池都处于充电状态,这些时段的电价都处于平时或谷时,园区从大电网购买低价的电能;而在第11~15和18~22时段,从大电网购电的价格最高,蓄电池开始放电,承担园区内的电负荷,减少在用电高峰时段从电网购买高价电能,蓄电池这种削峰填谷运行策略有效提高了微电网的经济性。大电网在第1~7和第23~24时段承担园区内主要的电负荷,这段时间的电价低也恰好位于谷时。在所有的电价的峰时段,微型燃气轮机都处于满负荷工作状态,在这些时段微型燃气轮机和蓄电池承担园区的电负荷,产生的多余电能出售给电网,而此时向大电网售电的价格最高,进一步实现了运行费用的减少。 图6 运行费用最低策略的蓄电池工作曲线 图7是运行费用最小时的冷、热能功率出力。在微型燃气轮机出力较低的第1~6和23~24时段,冷负荷完全由分体空调承担;热负荷则是使用蓄热槽内的热能承担。在微型燃气轮机出力较高的第8~16,燃气轮机产生的热量通过余热锅炉和溴化锂吸收式制冷机可以满足冷热负荷,产生的多余热量储存在蓄热槽中,此时分体空调停止工作。由于蓄热槽的容量限制,蓄热在第17时段达到蓄热量的上限,不再蓄热,但是微型燃气轮机仍然会产生多余的热量,此时会造成热量的浪费情况。 图7 运行费用最低策略的冷、热能功率出力 图8为优化结果中环境污染成本最低的运行策略的电功率曲线。系统内污染气体来自微型燃气轮机和大电网,且从燃气轮机和大电网排放的数学模型可以看出微型燃气轮机的环保性更优,在该种策略下燃气轮机的24小时的总出力为1 469 kW·h,明显高于最低运行费用策略的1 330 kW·h。另外,为了减小污染气体产生,燃气轮机生产多余的电能出售给大电网的情况也很少出现。 图8 环境污染成本最低策略的电功率出力 通过优化结果还可以看出,两个目标存在着制约的关系,无法同时达到最优,前文所述的两种运行策略是两个目标分别达到最优情况下的策略,优化结果中还包含其它折中的运行策略。选择基于Pareto最优解集的多目标优化方法的优势在于,用户自行决定对这两个目标的侧重程度,根据需求选择运行策略,更具灵活性和多样性。 4.2.3 算法比较 针对文中研究的问题采用传统MOGWO算法的得到Pareto解集,采用盒须图对两种算法求解所得Pareto前沿进行比较(图9)。各目标函数值分布越广,算法的全局搜索性能就越好。对比结果表明改进MOGWO的全局搜索性更优。为了消除算法随机性带来的误差,分别独立运行两种算法20次,对比结果与上述近似。另外,在对灰狼的位置初始化和更新方式调整后,改进MOGWO算法的求解速度明显快于传统MOGWO算法。 图9 优化结果对比 文中针对CCHP型微电网的多目标运行优化问题,构建了以运行费用和环境污染成本为多目标的运行策略优化模型,采用改进的MOGWO算法求解。结合仿真分析,对优化模型及算法的适用性和有效性进行验证,得到了下列结论: (1)通过对MOGWO算法进行狼群的初始化和更新方式的改变以及优化控制参数的调整策略,再结合微电网优化模型进行改进。改进MOGWO算法对微电网的多目标运行优化问题的优化结果全局搜索性和计算速度均优于原始算法; (2)对优化结果的分析表明,不同的优化策略通过改变各个微源的出力,可以对两个目标实现不同程度的优化,实现降低运行成本、减少污染气体排放的目标; (3)优化目标之间存在一定的制约关系,无法同时达到最优。本文建立的CCHP型微电网多目标优化模型可以让用户根据实际需要选择运行策略,优化结果具有灵活性与多样性。 CCHP型微电网的研究涉及运行优化、能效评估、微源模型建立与计算方法等多个方面;智能优化算法面对非线性多约束问题的优化能力有待提高,针对这些问题今后可以开展更深入的研究。3 改进多目标灰狼优化算法
3.1 多目标灰狼优化算法
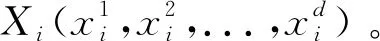
3.2 改进多目标灰狼优化算法
4 CCHP型微电网优化算例分析
4.1 基础数据
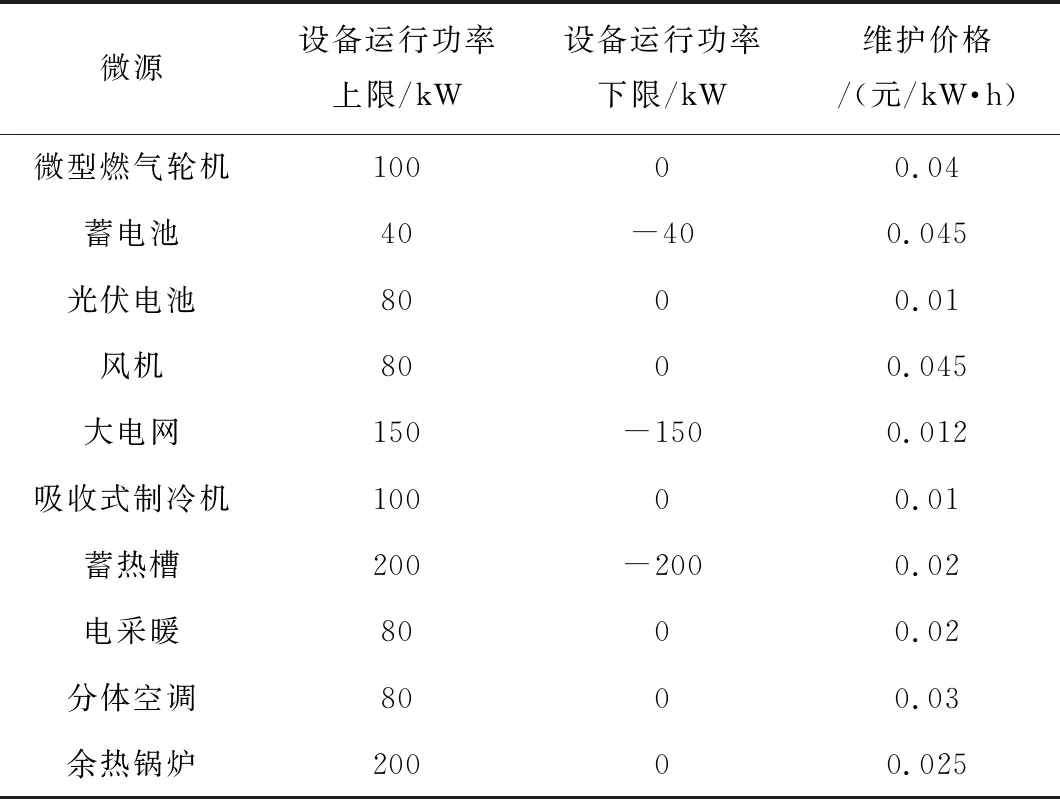
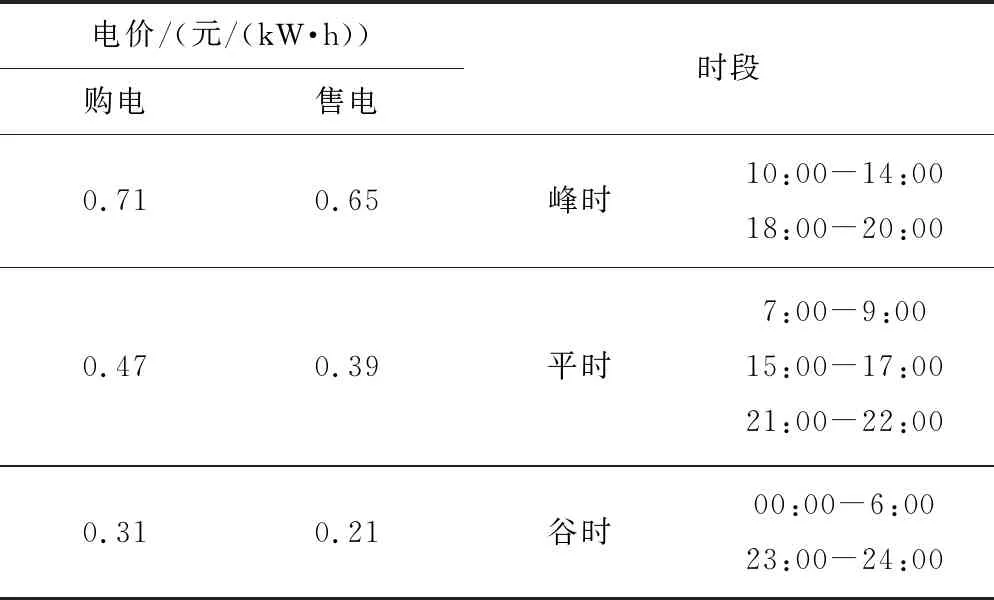
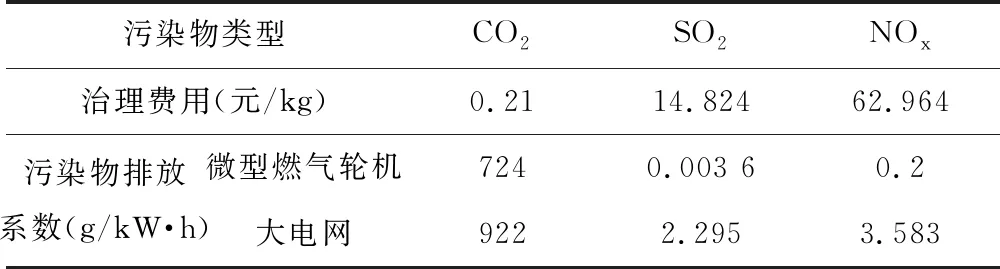
4.2 模型仿真及结果分析



5 结束语
