基于机器视觉的五轴点胶机转轴位姿求解

王 瑞，瞿佳伟，张春雷,

(1.四川大学机械工程学院，成都 610065；2.成都乐创自动化技术有限公司，成都 510107)

0 引言

随着现代制造业的不断发展革新以及精密复杂产品的层出不穷，对封装加工技术的要求不断提高，手机电脑等电子产品对零部件的封装精度要求更甚，因此五轴点胶机在封装加工领域大放异彩。但如果点胶机各联动轴之间存在几何误差，会导致点胶轨迹的偏移、点胶不均、轨迹不连贯等问题，因此想要提高点胶轨迹的完整度和精度，就必须对机床的各项误差进行精准的检测[1]。

现有五轴机床误差比较常用的测量方法主要有试件加工测量和仪器测量两种[2]。试件加工测量的方法主要是通过对标准试件进行切削加工，通过标准试件的加工误差来体现机床的几何误差。常用的仪器测量仪有激光干涉仪、球杆仪、R-test测量仪等，通过安装测量仪进行机床加工运动，从而直接测量出运动轴在各个方向上的误差[3-4]。

传统的测量方法奠定了现代五轴机床旋转轴误差的基础，为相关五轴机床误差测量实验提供了成熟的思路，但无论是标准试件加工测量、球杆仪、接触式探头还是改进球杆仪测量的6圈法测量，这些方法需要昂贵的测量仪器和繁杂的测量步骤，对测量仪的安装和测量的操作都有较高的要求，对于周期性机床误差检测来说，费时费力，影响加工效率[5-8]。

机器视觉本质是基于工业相机和图像处理技术模拟实现人眼的识别功能，应用该项技术能完成既定环境的特定任务,并提高机器自动化、智能化[9]。当前机器视觉已经在各个领域得到有效的应用，包括自动识别生成点胶加工轨迹，实现对刀点坐标的提取和精准对刀，实现对在载玻片点胶位置的实时监测和校正。这些应用的核心都是通过机器视觉获取图像信息，提取图像特征信息，从而建立相机像素坐标和现实空间的转换关系，最终得到高效的位置评估和校准手段[10-12]。现有的基于机器视觉的机床几何误差辨识方法和理论，大部分需要自定义的图案或设备，并且在转轴位姿已知的情况下对包括转轴转角的定位误差在内的机床几何误差进行辨识[13-15]。

在上述背景下，在未知转轴位姿并且适用于双转台的前提下，提出一种利用机器视觉来求解机床旋转轴位姿的方法。利用工业CCD相机拍摄不同机床坐标下的标准标定板照片，提取特征点坐标，通过机床几何误差模型和L-M优化得到最终的误差矩阵和转轴位姿。最后通过加工点跟随实验(即选取一个特征MARK点，将加工针阀对准该点，并获取此时的机械坐标，通过求得的转轴位姿对其进行坐标变换，最终对比计算所得机械坐标和实际对准MARK点的机械坐标坐标之差)来验证此方法的可行性和准确性。

1 建立运动学模型

五轴机床可分为单转台-单摆头、双摆头和双转台3类，方案研究的五轴点胶机属于双转台类型五轴机床，即转轴C固连在转轴A上，如图1所示。由于五轴点胶机的机械特性，存在着不可避免的几何误差，包括平动轴的3项垂直度误差，C轴相对于A轴的旋转和平移误差；A轴相对于Y轴的2项位置误差，A轴两项平行度误差，A轴的初始角度误差，共11项误差[16-17]。

图1 五轴点胶机结构图

五轴点胶机各运动轴之间通过移动副或旋转副相连接，形成一条加工运动链，用{V}表示相机坐标系，其他如图2所示。由于工件坐标系会随A轴旋转而改变，引入一个辅助坐标系{S}，来表示AC轴未旋转状态下的初始工件坐标系。将五轴点胶机的运动轴、针阀、工件以及基座均视为刚体，以加工过程中点胶点为分界点，从而将包括上述所有刚体在内的五轴点胶机机械结构划分为两条加工运动链[18]。

图2 五轴点胶机运动链

(1)

同理得到运动链中其他相邻两坐标系间的变换矩阵。建立如下两个方程式分别用于表征相机坐标系{V}到初始工件坐标系{S}中的实际刀具位置和刀具方向的变换关系：

(2)

式中，pW为刀具在工件坐标系下的齐次坐标；vW为刀具在工件坐标系下的向量。

采用的误差处理方法是将所有误差耦合成一个整体的变换矩阵，引入矩阵RVW来表示这种变换关系，此时工件坐标系到相机坐标系的变换关系可以用下式表示：

pV=RVWpW

(3)

(4)

式中，pV为相机坐标系某一点的齐次坐标，变换矩阵RVW∈R4，将矩阵RVW分为4个部分，其中矩阵RVS∈R3，向量MT∈R3×1。将各项误差符号代入，通过符号计算得出其形式表达如下：

(5)

2 初始解求解

根据第1节建立的五轴点胶机运动学模型如图3所示。把机床的运动分为两个阶段，平动轴的移动和转动轴的转动。

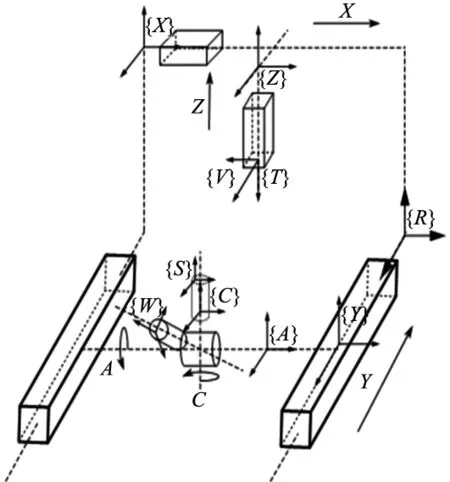
图3 五轴点胶机运动学模型

2.1 平移状态

当机床A、C轴保持0°初始状态，坐标系{S}与坐标系{W}重合,则pS=pW，pS为坐标系{S}下一点。

则此时式(4)中表示旋转状态的子矩阵RVS为常数矩阵，可将表达式转化为：

(6)

根据标定板得出的相机内参，获得每张照片对应外参，得到工件坐标系{W}和相机坐标系{V}间的转换关系：

(7)

式中，R、t为相机外参参数；0T和1分别表示3×3的旋转矩阵和3×1的平移向量。

根据式(6)和式(7)，可以得到：

(8)

式中，RVS的物理意义为辅助坐标系平面到相机坐标系平面转换的旋转矩阵，理论上来说所有仅平移XYZ三轴得到的工件坐标，其对应的RVS是相等的，采集n组仅平移的图片的数据，通过获取所有平移图片的外参旋转矩阵，对其取平均值：

(9)

式中，Ri为第i张图片的外参旋转矩阵。

根据前文可以知道MT是机床坐标与各项误差映射得到，引入一个HVSM∈R3×4矩阵来表示这种映射关系：

HVSM(XiYiZi1)T=ti

(10)

式中，ti为第i张图片外参平移向量；Xi、Yi、Zi为第i组机床坐标，由此可建立线性方程组，根据式(9)、式(10)求解出矩阵RVS、HVSM，由此给定任意机械坐标，即可知道此时该点从坐标系{S}到坐标系{V}的变换关系。

2.2 旋转状态

当A轴转动时，可以得到辅助坐标系上一点和工件坐标系之间的转换关系：

PW=RA(PS-ta)+ta

(11)

(12)

式中，ta为A轴上一点；va为A轴的转轴向量；θ为A轴旋转角度；RA为坐标系绕A轴旋转的旋转矩阵，由罗德里格斯公式可得。

由式(7)、式(11)可求得仅A轴旋转下{Y}到{V}的表达式：

pV=R·RA·pY+R·(E-RA)·ta+t

(13)

根据第2.1节的结果，令机械坐标为pM可以得到：

pV=RVS·pS+HVSM·pM

(14)

联立式(13)、式(14)可以得到：

(15)

根据上式可求解出va、ta的初始解；同理可求得C轴在坐标系{C}下的向量vc，和轴上一点tc。

3 L-M优化

通过对初始解进行实验验证，机床运动后的坐标位置误差超出可接受范围，因此需要对解值进行优化。L-M算法是对Gauss-Newton算法的改进[19-20]，通过添加阻尼因子，使得迭代收敛的鲁棒性更好，参考宋占峰等人的优化方案[21]，通过L-M算法来对转轴位姿进行优化。

3.1 优化模型

将第2节求得的转换矩阵和转轴位姿视为优化目标，目标函数为n张标定板照片上的m个点在相机坐标系下的理论值和测量计算值之差的模的和最小，表达式为：

(16)

(17)

根据L-M算法的数学推导可知：

(18)

式中，Jk、ΔXk为第k次迭代自变量的雅克比矩阵和搜索步长。

对其进行求导并令结果为0，可以得到搜索步长的表达式：

(19)

第k次迭代自变量的雅克比矩阵表达形式为：

(20)

3.2 参数设置

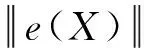
(21)

对于某一步的迭代求解值ΔXk不一定是有效的，为了筛选和调整搜索步长，引入增益比ρ表示实际优化量和预测优化量的比值：

(22)

只有当当前迭代的搜索步长和方向使得代价函数下降时，搜索步长才是有效性的，通过以下判断：

(23)

μk依据增益比来进行调整：

(24)

L-M算法的参数设置和流程如图4所示。

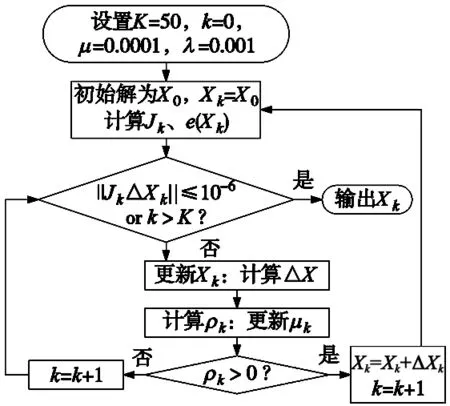
图4 L-M算法流程

4 实验验证

4.1 实验场景布置

实验选用大恒图像IMAVISION的MER-132-30UM-L工业相机，LED光源，7×7圆点标定板。利用双转台五轴点胶机来验证求解方法，将工业相机安装在Z轴上，标定板放置于跟随C轴旋转的工作台中心位置，实验现场如图5所示。

图5 实验现场

4.2 实验设置及结果分析

在保持照片清晰度的前提下拍摄标定板离相机不同Z轴距离的3组照片，每组Z轴相差5 mm，按照九宫格排布拍摄9张不同XY轴坐标下的照片，总共27张平动标定板照片；A轴在[-20,20]区间每旋转4°采集一次，C轴在[-180,180]区间每旋转30°采集一张，总共22张旋转标定板照片。图6为实验采集的部分不同角度标定板照片。

图6 拍摄的标定板照片

采集转轴转动的标定板照片，应当遵循光源良好，图片清晰，照片位置分布均匀的原则。所有拍摄的标定板保持在照片的中心位置附近，以此来避免相机镜头的畸变带来的像素点坐标误差。

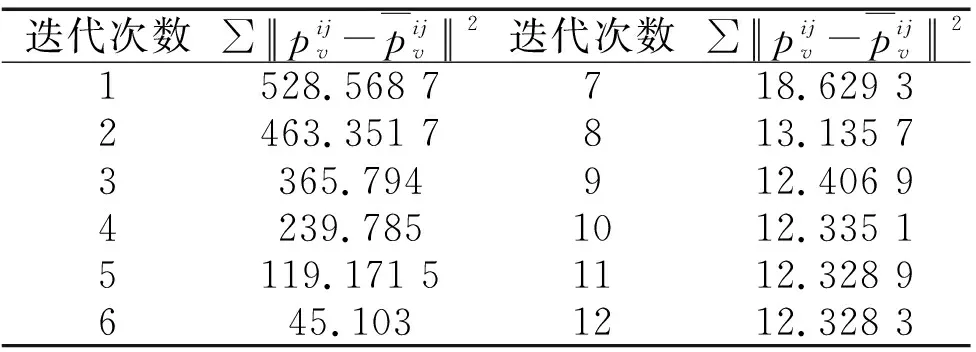
表1 L-M迭代过程的参数指标

由上表可以看出迭代次数在10次之后迭代残差就没有了明显的下降趋势，所以可以通过设置迭代的上限来提高L-M迭代的效率，将迭代次数k的阈值设置为20次。

4.3 方案鲁棒性验证结果及分析

为了验证L-M优化使用不同的搜索步长对迭代过程和结果的影响，设置了8组对照的搜索步长对照试验，获取不同的迭代优化解值，得到实验结果如表2所示。

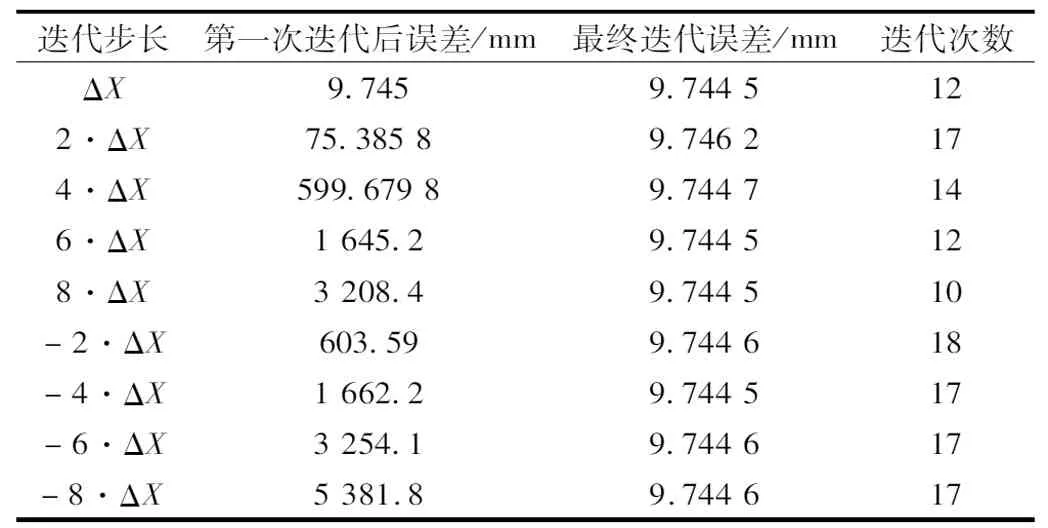
表2 不同搜索步长的L-M优化

由表2可知，虽然不同的迭代步长会影响初次迭代的结果，这某种意义上代表了不稳定的初始解值输入，但最终都解出几乎相同的优化解值。

最后为了验证L-M优化是否可以获得更准确的结果以及标定采集的照片对实验结果的影响，在采集标定照片时，将标定板放置在工作台的中心，左上角，右下角，3种不同位置，通过相同流程采集标定照片，得到初始解，具体实验分组如表3所示。

表3 采图实验分组信息

为了简化实验流程，直接在标定板上进行结果验证，选取标定板上的唯一特征点作为MARK点，将相机十字光心对准MARK点，记录当前机械坐标格式为[X,Y,Z,A,C]，利用求得的转轴位姿参数计算得到旋转后的机械坐标，将针阀移动到对应的机械坐标，如图7a所示，对准MARK实际坐标，如图7b所示。

(a) 对准坐标前 (b) 对准坐标后图7 MARK坐标误差对比

6组对照实验得出的最终解依次用于24组加工点跟随实验，得到最终MARK点机械坐标的欧氏距离平均误差结果如图8所示。

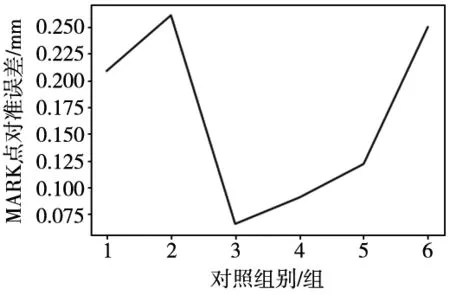
图8 对照实验误差图

由图8可知，将标定板安装在工件台中心位置进行照片采集，最终得出的结果误差最小。并且优化解值相对于未优化解值，得出的结果误差也更小，证明优化算法有效。最终采图方案遵循标定板位于工件台中心，并且位于照片的像素中心，得出初始解，再进行L-M优化，得到24组实验数据的误差平均值。数据表明此方案求解的转轴位姿，用于实际加工后的欧氏距离平均误差为0.066 mm，部分数据如表4所示。

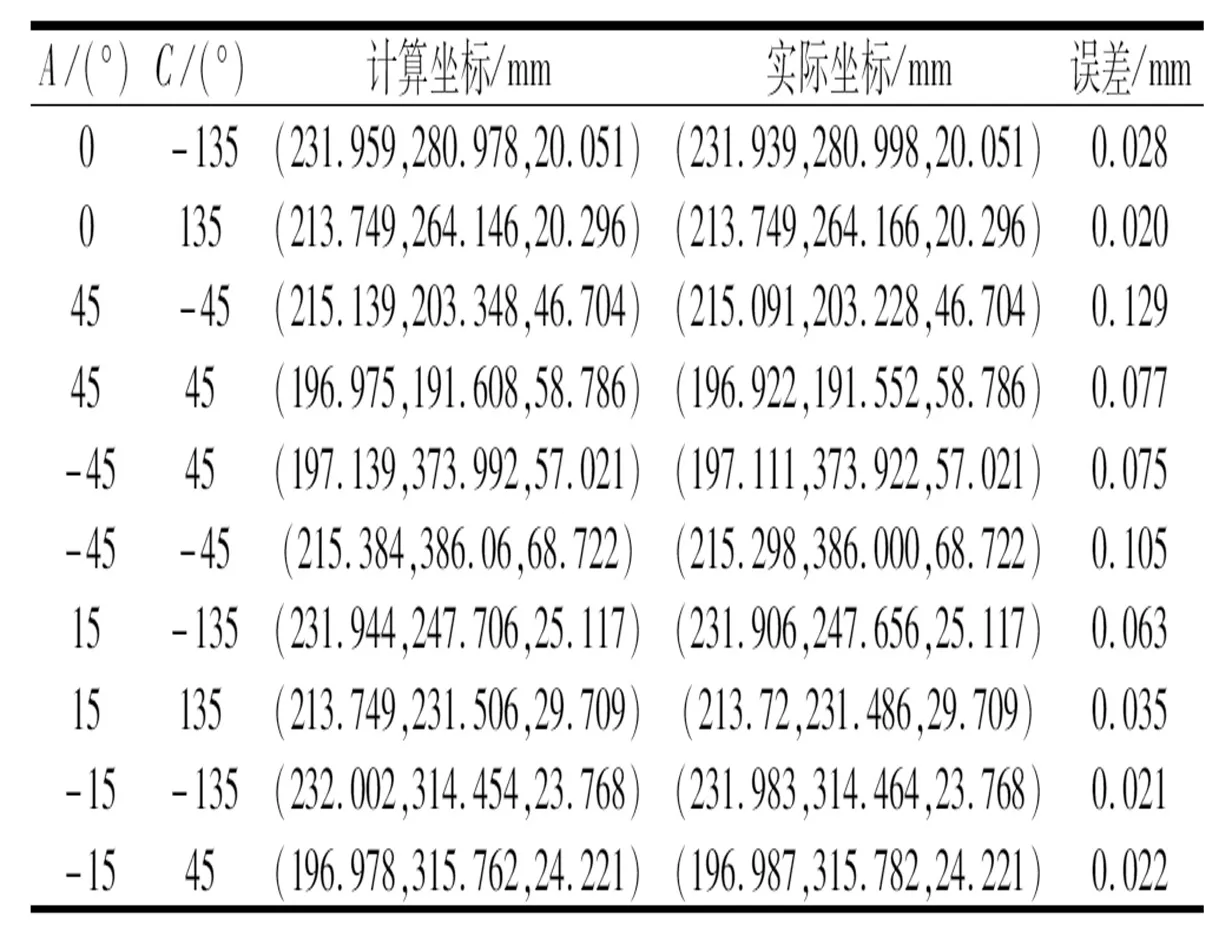
表4 计算坐标与实际坐标对比表

5 结论

(1)基于机器视觉求解五轴点胶机转轴位姿的方法是可行的。经过采图对照实验验证，将标定板安装在工件台中心、保持良好光源、标定板位于照片的像素中心可以获得最准确的转轴位姿解值，满足了五轴点胶机的实际加工需求。通过L-M迭代步长对照实验，证明算法具有良好的鲁棒性。

(2)本文算法可以通过编程将其模块化，嵌入机床操作软件中，简化机床转轴位姿标定的过程，提高加工效率。

(3)目前视觉采用的是二维图像，对深度信息的获取不够准确，未来可以借助3D相机来获取图像的深度信息，得到精度更高的空间坐标，并利于算法优化，进一步提升求解的转轴位姿精度。